变阻抗桩非自由端竖向瞬态激振动力响应分析方法及应用*

吕述晖，陈章宇，桑登峰

(1.中交四航工程研究院有限公司，广东 广州 510230；2.中交交通基础工程环保与安全重点实验室，广东 广州 510230；3.南方海洋科学与工程广东省实验室(珠海)，广东 珠海 519082)

灌注桩是港口码头工程中常用的基础形式之一，其采用现场成孔并灌注混凝土成桩。由于成桩工艺特点及地质条件的复杂性，灌注桩的成桩质量不易控制和保证，容易在灌注混凝土过程中出现断桩、缩颈、离析、露筋和夹泥等现象。在港口码头工程近岸和离岸结构中使用的灌注桩，通常由于水上成桩桩位处的泥面低于水面的特点，需要采用先施打钢护筒入泥面一定深度，后钻孔成桩的工艺。对于泥面较深或泥面软弱土层较厚的工况，所需要的钢护筒较长，且浇筑混凝土后钢护筒一般不再拆除。由于长钢护筒的使用，采用低应变反射波法检测灌注桩桩身质量时常遇到以下问题：1)钢护筒段桩身阻抗与无钢护筒段桩身阻抗不同，主要表现在钢护筒本身增加了桩身阻抗，以及钢护筒段桩径固定且一般大于设计桩径，导致该段桩身阻抗与无钢护筒段桩身阻抗不同(由设计以及成孔孔径所致)；2)钢护筒顶高程一般高于浇筑后混凝土顶面的高程，视桩顶设计高程的要求以及施工便利的考虑，二者之间差异可能较大，此时低应变检测时，桩顶实际并非自由端，特别当桩身上部存在显著缺陷，常采用凿除缺陷及缺陷以上钢护筒内混凝土的处理方法，凿除已知缺陷后须对缺陷以下桩段进一步检测或分段补浇混凝土后须检测浇筑混凝土以及新旧混凝土面的粘接质量，这类工况下，激振面同样不是自由端。上述问题的特殊性导致带长钢护筒灌注桩低应变反射波曲线较复杂，缺陷的辨识较困难。

结合解析算法或有限元方法对反射波曲线进行模拟，能够有效地辅助复杂反射波曲线的分析[1-3]。但相比有限元方法而言，解析算法能够更快速地拟合桩身复杂阻抗变化、土层参数变化对反射波曲线的影响，因此其常用于基于实测低应变曲线的缺陷反演分析[4-5]。而现有针对变阻抗单桩竖向瞬态动力响应的时域解析算法[6]和频域半解析算法[7]均是根据桩顶自由端激振建立边界条件，然后采用阻抗递推方法计算得到桩顶的速度时程曲线，对于激振面非自由端(桩身任意位置激振)的瞬态动力响应问题仍有待研究。

针对上述问题，本文通过建立简化的数学模型，提出桩身任意位置竖向激振的瞬态动力响应问题的半解析方法，并应用于带长护筒灌注桩的反射波曲线分析，通过结合设计、施工参数对可能工况进行模拟，辅助分析桩身完整性情况。本文方法可为解决类似工程问题提供借鉴和参考。

1 变阻抗桩非自由端竖向瞬态激振动力响应分析方法

1.1 简化分析模型建立

本文针对带长钢护筒灌注桩涉及的变阻抗桩非自由端竖向瞬态激振动力响应问题进行研究，所采用的简化桩-土体系分析模型见图1。由图1a)可看出，钢护筒顶高程高于混凝土顶面高程，钢护筒底入泥面一定深度，瞬态激励荷载施加于混凝土顶面。分析时，钢护筒段(内无钢筋混凝土，长度L3)、钢护筒+钢筋混凝土段(长度L2)、钢筋混凝土段(外无钢护筒，长度L1)均考虑为黏弹性一维杆件，段与段界面考虑位移和力的平衡条件。对于桩身缺陷的模拟参考文献[8]的方式，即对于阻抗线性突变，将该段独立为有限长一维杆件并考虑其两端与相邻上下桩段的位移和力连续条件即可建立这类变阻抗问题的竖向振动控制方程并求解；对于阻抗线性渐变、非线性渐变及复合变化可将该段沿桩身纵向离散简化为一系列圆柱体，圆柱体薄片的截面几何尺寸根据实际尺寸轮廓确定。

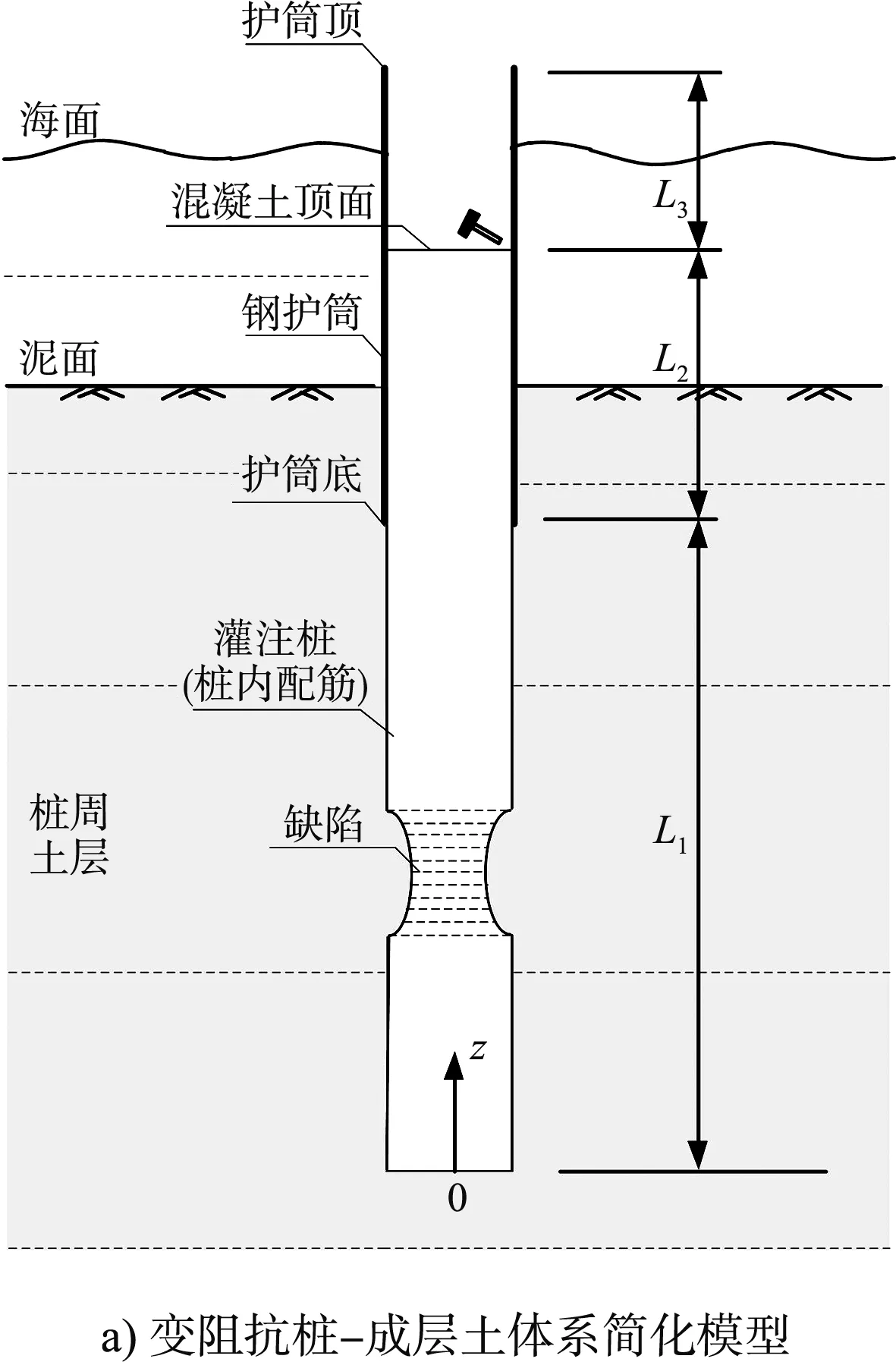
注：zk、zk+1分别为以桩端为原点的k桩段的顶面、底面竖向坐标值；Qk、Wk分别为k桩段的轴力、纵向位移。

1.2 数学问题建立及求解

根据一维黏弹性杆件纵向振动理论，采用Laplace域方程描述桩的纵向振动行为：

(1)

s=iω

(2)

χk=EpkAk+Akδpks

(3)

(4)

式中：Wk=Wk(z，s)为第k桩段(离散后任意桩段)的纵向位移，其中z为以桩端为原点的竖向坐标值；ω为角频率；Fk(z，s)为桩侧摩阻力；Epk、δpk、ρpk、rk分别为第k桩段材料的杨氏模量、阻尼系数、密度以及桩段半径。对于钢护筒+混凝土桩段，考虑钢护筒截面阻抗与混凝土桩截面阻抗叠加，计算等效的桩段截面积，该桩段的其他材料参数则仍取混凝土的材料参数。

桩端土层对桩的作用简化为黏弹性支承，黏弹性参数中刚度系数kb和阻尼系数δb按Deeks等[9]提出的方法确定：

(5)

(6)

式中：Gsb、vsb、υsb、rp1分别为桩端土的剪切模量、剪切波速、泊松比以及桩端截面半径。

桩侧土与桩之间的动力相互作用采用平面应变模型[10]模拟，即桩侧土作用于桩侧的剪切刚度为：

(7)

(8)

(9)

(10)

式中：K0、K1分别为零阶、一阶第二类虚宗量Bessel函数；vsk、Gsk、ρsk、βsk分别为第k桩段侧土的剪切波速、剪切模量、密度和阻尼系数。

由式(1)(7)可求解得到第k桩段的纵向位移Wk和轴力Qk如下：

(11)

(12)

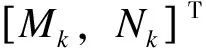
根据桩段之间的位移连续和轴力平衡条件(式(13)为非激励位置，式(14)为激励位置)以及式(15)(16)所示的桩底、桩顶的边界条件，可联立矩阵方程求解系数矩阵。

(13)

(14)

(kb+δbs)W1|z=0=Q1|z=0

(15)

Qk|z=L1+L2+L3=0

(16)

式中：zk为第k桩段顶距桩底的轴向距离，见图1b)；P0为施加于桩顶的竖向升余弦脉冲激励力p(t)=pmax[1-cos(ω0t)]/2(0≤t≤2π/ω0)的频域形式(t为时间)，具体为：

(17)

式中：pmax为激振力峰值；ω0为激振力角频率。

求解得到系数矩阵后，可进一步由式(18)计算桩身任意位置的速度频域响应vk，然后通过离散傅里叶逆变换计算速度时域响应。

vk=sWk

(18)

2 工程实例及分析

某高桩码头采用灌注桩基础形式，灌注桩设计桩径1 500 mm，设计桩长44.1 m，混凝土强度等级C40；采用回旋钻+冲击钻成孔；泥面以上及泥面以下一定深度采用直径1 500 mm、壁厚10 mm的钢护筒；该桩所在位置主要地层为砂、胶结砂层；护筒顶、护筒底、护筒内混凝土顶面、桩底、泥面高程见表1。工况1为成桩后首次检测时对应工况，此时，由于混凝土浇筑过程中发生堵管等问题(高程-4.0 m以上为堵管可能影响深度范围)，浇筑中断，未浇筑到设计桩顶高程；由于浇筑过程异常导致桩身浅部混凝土存在离析、泥浆污染等问题，遂采取钢护筒内凿除异常混凝土，直至揭露新鲜完好混凝土面(高程-4.0 m)。为检测该位置以下桩身的完整性情况，进行第2次检测，即对应工况2；检测完成后，混凝土面凿毛并涂抹胶黏剂后，重新浇筑混凝土至护筒顶，进行第3次检测，对应工况3。

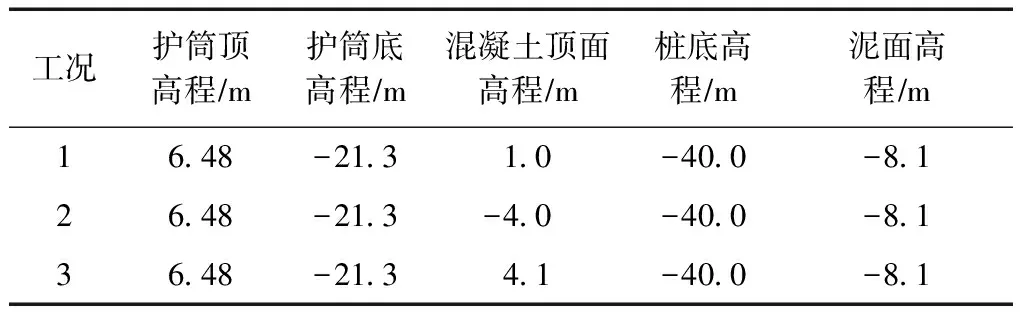
表1 灌注桩各断面高程

3次检测获得不同的低应变反射波曲线见图2。由图2a)可知，由于浅部混凝土质量异常，低应变曲线出现显著振荡，难以直观判断桩身完整性情况。凿除质量异常混凝土后，图2b)中实测低应变曲线震荡明显减少，更有利于缺陷判别，但浅部约8.0 m处仍出现异常同相反射。根据表2所列桩参数以及表3所列土层参数(土层计算参数根据土性按经验并拟合临近完整桩低应变反射波曲线确定)模拟计算反射波曲线表明，该同相反射与护筒顶反射信号位置接近，因此考虑为护筒顶反射引起反射波异常。第3次检测目的在于进一步验证第2次的检测结论(高程-4.0 m以下无明显桩身缺陷)以及检测新浇筑混凝土的质量，实测曲线表明，桩身无明显缺陷，新老混凝土界面结合良好。

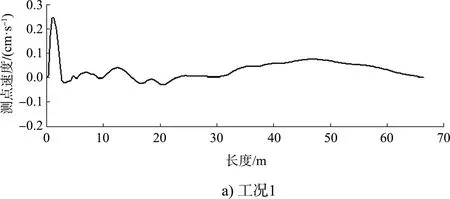
图2 实测速度反射波曲线与模拟计算曲线对比

表2 桩参数取值

表3 土参数取值

图2b)中，采用与解析计算相同的桩身参数及激振脉冲参数(但不考虑桩周土)，通过三维有限元模拟工况2得到反射波曲线。可以看出，解析计算曲线与有限元计算曲线均可见明显的护筒顶反射，且可清晰分辨第1次和第2次反射信号，但实测曲线中，第1次护筒顶反射信号幅值较数值计算曲线小，第2次护筒顶反射信号幅值则几乎难以分辨。上述差异表明，实际检测时，波动能量的衰减更为明显。此外，混凝土面以上裸露的长钢筋笼尽管无法类似于钢护筒产生可辨识的端部反射，但将分担部分激振能量。图2c)中，解析计算曲线中泥面反射和护筒底砂层中的显著扩径反射信号与实测结果吻合较好。

3 结论

1)采用本文方法可以较好地模拟钢护筒、泥面、护筒底扩径等桩身阻抗变化对桩身任意位置竖向瞬态激振获得的反射波曲线的影响。通过模拟分析实际工况，可以辅助分析低应变反射波曲线，判断桩身缺陷情况。此外，本文方法也可用于分析单桩任意位置激振和拾振获得的反射波曲线。对于桩顶存在上部结构的工况，可以将桩顶截面处上部结构阻抗作为桩顶边界条件，采用本文算法分析既有结构物下的基桩动力响应问题。

2)在低于钢护筒顶的护筒内混凝土顶面激振和拾振获得的反射波曲线中，护筒顶1次反射信号与激振信号同相，2次反射信号与激振信号反相，这与激振面以下桩身缺陷的多次同相反射信号有所区别。由于受波动能量耗散以及裸露钢筋笼的影响，护筒顶反射信号较模拟计算值衰减更为显著。上述特征有助于类似带长钢护筒灌注桩的缺陷识别和分析。