使用CNN-SVR的汽车组合仪表组装质量预测方法

2022-04-18李育锋吴鹏程刘德高

中国机械工程 2022年7期

何彦肖圳李育锋吴鹏程刘德高杜江

1. 重庆大学机械传动国家重点实验室，重庆，4000302.重庆矢崎仪表有限公司，重庆，401123

0 引言

汽车组合仪表直观反映车辆实时运行情况，是提供驾驶参考、保障行车安全的重要工具，其生产过程主要分为印制电路板(printed circuit board，PCB)表面贴装、元器件组装两个环节。组装过程包括显示器安装、指针压入等多道与指示部件直接相关的工序，共同决定着仪表产品的组装质量[1]，组装过程成为汽车组合仪表产品质量控制的关键。

为切实保障汽车组合仪表的组装质量，需在质检环节中设置众多检查项。汽车组合仪表生产是典型的多品种、小批量生产，沿用上述方法会增加产品时间成本，导致员工技能要求变高、设备巡检难度增大等生产管理问题，因此研究不同生产数据对仪表产品质量的影响并尽早预测组装质量[2]，对于提高仪表厂商生产效率具有重要意义。

汽车组合仪表生产过程中，各类传感器及检测设备采集并存储了大量生产过程基础数据，通过建立准确有效的预测模型，可以用来衡量产品组装质量[3]。传统的统计回归建模预测方法通常依靠人工经验选择过程参数及数据特征。KIRCHEN等[4]提出一种增量回归质量预测方法对轧制金属板材的厚度进行分析。刘银华等[5]通过提取多元检测数据主向量并构建偏最小二乘回归(PLSR)模型，实现了车身产品多工位装配偏差预测与质量控制。

随着仪表生产过程自动化程度的提高，各工序间的联系越发紧密，影响产品质量的过程因素作用机理复杂。传统依靠人工经验的统计建模方法受领域知识限制、特征选择标准不一等影响，难以得到精确的预测模型。利用神经网络、贝叶斯网络、支持向量机等机器学习方法能够处理高维、复杂的数据，更易获得适用的质量预测模型[6]。GONZALEZ-VAL等[7]使用卷积神经网络(CNN)提取钢材的激光焊接红外图像特征，用于预测焊接过程的缺陷位置。ZHU等[8]结合时频表示和多尺度卷积神经网络(MS-CNN)提出一种新的特征学习方法，用于预测轴承服役过程的剩余使用寿命。SUN等[9]基于粒子群优化的反向传播神经网络(PSO-BPNN)对航空发动机多级转子装配的同轴度和垂直度做出预测。WAN等[10]采用多元线性回归分析(MLR)和反向传播神经网络(BPNN)提取特征对动态电阻进行测量，提高了钛合金点焊质量估算的准确性。杨洲等[11]构建了贝叶斯网络(BN)简化推理模型，对机载自动驾驶仪进行故障预测与健康评估。ZHENG等[12]利用先验概率分布构建贝叶斯网络对质量的影响因素，提出基于MapReduce并行计算模型的贝叶斯网络与大数据分析集成方法，对船体分段制造过程进行质量分析与控制。朱大业等[13]应用基于支持向量机(SVM)的蒙特卡罗法，对复杂非线性系统的不确定度评定结果做出预测，保证了车辆座椅的质量可靠性。叶永伟等[14]提出了基于最小二乘支持向量机(LS-SVM)的温度误差预测方法，对温度仪表的测量值进行补偿。SONG等[15]提出功率参数调节的支持向量回归(SVR)模型，实现了激光增材制造过程稳定准确的产品成分预测。

由于仪表组装过程各工序相互影响，因此生产过程数据呈现出非线性、相关性的特点，不满足贝叶斯网络建模的特征独立性要求。同时，建模过程还需先验经验来确定特征概率分布，但实际生产中的特征分布参数总是不断变化的，固定分布参数不能全面反映仪表生产情况，导致建立的质量预测模型存在系统误差。

基于神经网络的预测方法针对经验风险进行优化，无法避免收敛于局部最小值的问题[14]。基于支持向量机的预测方法可减小结构风险[16]，引入正则项可以有效解决过拟合问题，但需要借助二次规划来划分分隔超平面，在规模较大的仪表生产过程数据上构建预测模型，其计算复杂度会显著增加，还将耗费大量运算时间，这在实际生产中不够经济有效。

在仪表产品组装质量预测过程中，如何对大量生产过程数据进行特征提取直接影响模型的预测性能。而在众多工业领域中，各种高效的特征提取方法已有广泛的应用。李兵等[17]结合时域特征提取和集合经验模态分解法，对电机轴承运行数据进行特征向量的构造。SUI等[18]采用信息熵与Gram-Schmidt正交变换相结合的方法选择有效的热轧工艺参数，构建特征子集并将其作为预测模型的输入。张妍等[19]基于Relief算法筛选航空发动机的退化特征，利用主成分分析对特征进行提取来预测剩余使用寿命。ZHU等[20]对轴承运行数据进行短时傅里叶变换，并在CNN中设置两个卷积层获取深层次特征，提高了模型的泛化能力。基于神经网络的特征提取方法无需先验知识便可从数据中获取特征，避免了人为设计特征不够全面、不够可靠的弊端，有助于发挥仪表产品生产过程数据的优势[21]。

针对上述问题，本文提出一种基于卷积神经网络(convolutional neural network，CNN)和支持向量回归(support vector regression，SVR)的汽车组合仪表组装质量预测方法。搭建卷积神经网络对原始生产过程数据进行自适应特征提取，通过抽象表示特征替代人工设计的特征，在保留原有数据信息基础上降低了计算复杂度，避免传统数据驱动方法对特征提取和特征选择的依赖。并将提取的特征作为支持向量回归模型的输入，利用网格搜索(grid search)算法优化模型参数，对指针偏转角度做出准确预测，以反映汽车组合仪表组装质量。最后在汽车组合仪表生产线上对预测方法的有效性与泛化性进行了验证。

1 仪表组装工艺分析及质量预测流程

1.1 仪表组装工艺分析

指针式仪表是最常用的汽车组合仪表[22]，典型指针式仪表的组装过程如图1所示。

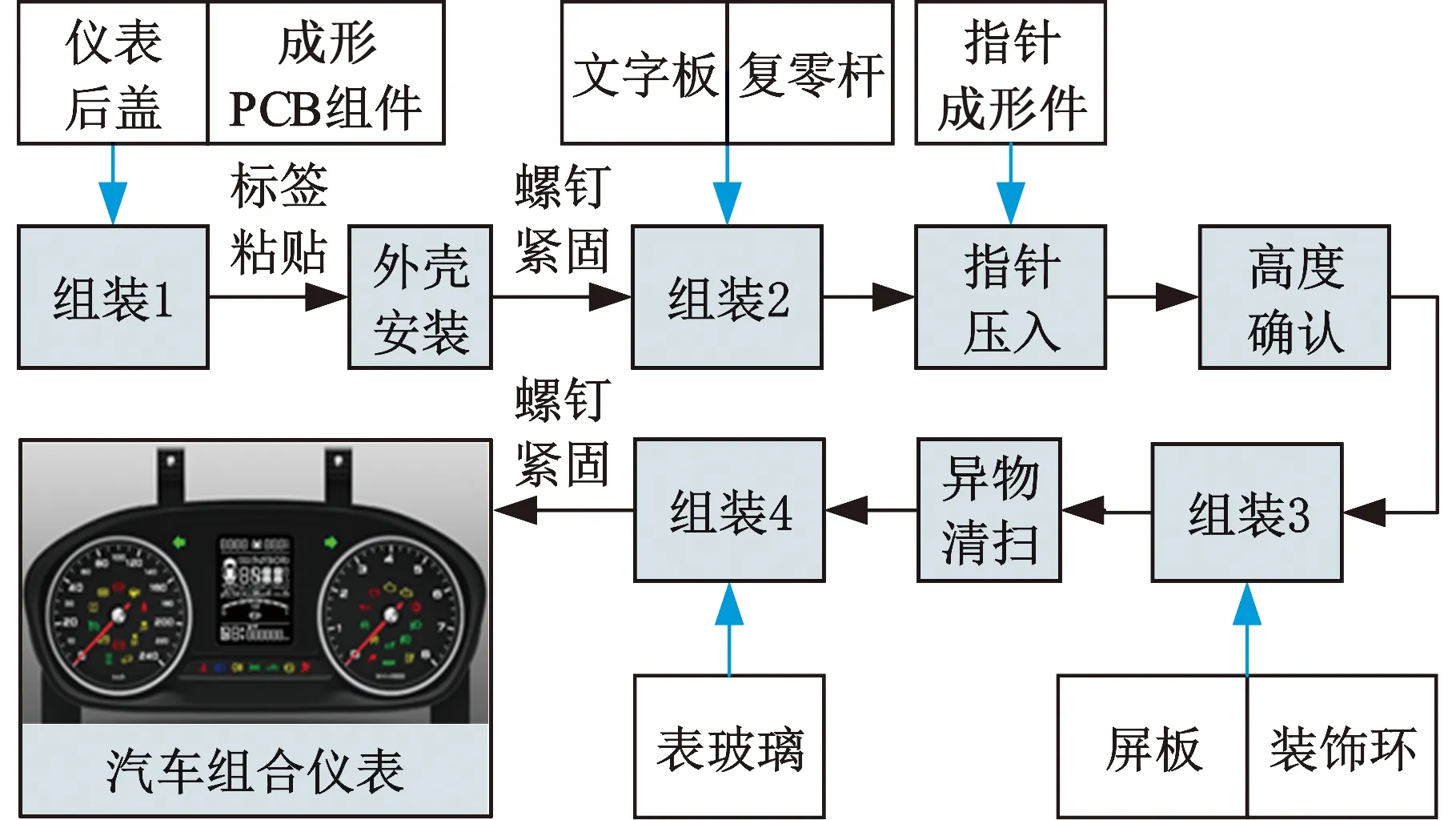
图1 指针式汽车组合仪表组装工艺流程

组装完成后需对仪表产品进行机能检查及外观检查。机能检查主要包括表盘0位置示值补正、静态待机电流检测、指针动作检查等，具体仪表产品机能检查项目及耗时情况如表1所示，可以看出，对车速表、转速表进行指针动作检查的耗时共60 s，在合计耗时中的占比高达35.1%，对生产效率的影响显著。因此亟需智能化方法对指针动作检查结果做出准确预测，提前掌握指针在各速度/转速段的偏转角度，以改善机能检查流程。

表1 典型仪表产品机能检查流程及耗时

1.2 汽车组合仪表组装质量预测流程

基于卷积神经网络和支持向量回归(CNN-SVR)的汽车组合仪表组装质量预测方法流程如图2所示。

通过现有的指针压入设备、关键工序检测系统、视觉检测系统等获取仪表生产过程数据。通过CNN分别对模型训练数据和测试数据进行自适应特征提取，形成训练集和测试集。训练集用于训练得出SVR预测模型。在测试集上对仪表指针动作检查结果做出预测：若预测结果在工艺许可范围内，则在机能检查中略过指针动作检查环节；若预测结果异常，则产品需进行指针动作检查，待实际测试合格后进行外观检查。

2 基于CNN-SVR的组装质量预测模型

针对汽车组合仪表的质量预测模型结构如图3所示，主要分为CNN特征提取和SVR预测两部分。CNN需设置多个层次来实现特征提取，包括卷积层(convolution layer)、池化层(polling layer)以及在特征输出节点间设置的全连接层(fully connected layer)；提取后的特征则作为SVR的输入向量，得到指针偏转角度预测值(用于表征仪表组装质量)。

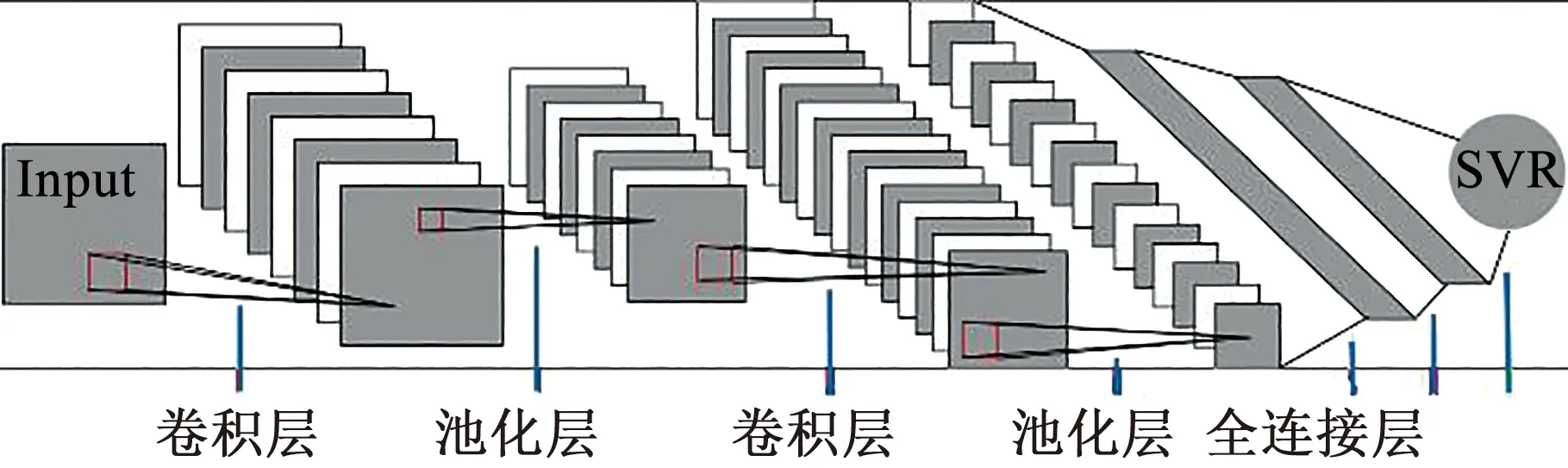
图3 CNN-SVR预测模型结构

2.1 卷积神经网络

2.1.1卷积层

CNN的卷积层通过卷积核对输入数据进行卷积操作，利用非线性激活函数构建输出特征向量，该过程可以用以下数学模型描述：

(1)

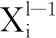
在每个卷积层之后引入激活函数，用于提高卷积操作后模型的表达能力，常用的激活函数有sigmoid函数、tanh函数、修正线性单元(rectified linear unit，ReLU)等。本文选择形式简单、计算速度更快的ReLU作为卷积层的激活函数，其表达式如下：

ReLU(t)=max(t,0)

(2)

式中，t为卷积操作后的特征矩阵中的神经元值。

为使卷积后的特征尺寸与输入特征保持一致，卷积前对输入特征进行零填充(zero-padding)。如图4所示，将卷积核与输入特征中相同尺寸区域的神经元进行卷积，按设定的步长(stride)进行滑动，重复以上卷积过程直至完成对整个输入的扫描。

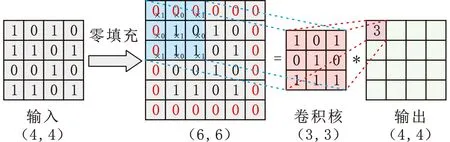
图4 卷积过程

2.1.2池化层

池化层在卷积层之后，通过向下采样压缩特征矩阵，可不影响特征的质量[23]，并降低特征维度。主要的池化方法有最大池化、随机池化、均值池化等，本文采用最常用的最大池化。如图5所示，通过2×2的窗口，按照步长依次给出相邻矩形区域内的最大值。

图5 最大池化方法

2.1.3全连接层

经卷积层和池化层处理后输出的特征向量被传递至全连接层，由多个全连接层对其进行整理分类。为了提高CNN性能，同样选择ReLU作为全连接层的激活函数。为避免输入特征数目过大带来潜在的过拟合问题，引入Dropout策略，随机隐藏神经网络中的部分连接。

本文将仪表产品生产过程数据作为输入数据。卷积层中，卷积核按照设定的步长在输入矩阵上进行滑动，通过卷积计算得到输出矩阵；池化层对该矩阵中不同区域的特征进行选择，以获取更加集中有效的特征信息。通过交替的卷积-池化操作，仪表产品生产过程数据中的隐含特征被提取，最后将提取好的特征传输到全连接层，实现特征向量的输出。

2.2 支持向量回归

使用支持向量回归(SVR)算法对汽车组合仪表进行质量预测可视作求解以下优化问题：

(3)

其中，xi∈Rn为输入的特征向量；ωTφ(xi)+d为分隔超平面，φ(xi)将样本特征映射到一个更高维的特征空间中，ω∈Rn为分隔超平面权重矢量，d为偏差量；yi为目标值，代表仪表产品机能检查指针偏转角度；ε为不敏感损失值，当且仅当预测与目标值差值的绝对值大于ε时才计算损失；ξi为松弛变量；C为惩罚因子，表示对离群值的重视程度大小，较大的C使模型对样本的拟合性更佳，模型更为复杂。

输入空间内存在部分线性不可分数据，为准确划分分隔超平面，引入核函数K(xi,xj)将输入数据映射到更高维空间，使样本数据在映射后的特征空间内线性可分，从而解决非线性回归问题。本文选择性能优异的径向基函数(radial basis function，RBF)作为核函数[24]，其表达式如下:

(4)

式中，σ为核函数宽度。

最终得到回归预测模型为

(5)

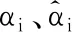
3 汽车组合仪表组装质量预测案例分析

3.1 数据描述

本文以重庆矢崎仪表有限公司生产的15B1型汽车组合仪表为研究对象，对提出的组装质量预测方法进行验证，该产品主要由车速表、转速表构成，其外观如图6所示。

图6 15B1型汽车组合仪表

研究数据源于产品组装车间质量检测系统，主要数据获取设备如图7所示。通过指针压入设备内置的力传感器、距离传感器分别对组装过程中的车速表(A点)和转速表(D点)的指针压入力F、压入高度H进行采集；使用示值补正设备获取指针0位置示值补正θC的数据；通过视觉检测系统对不同车速/转速下的指针偏转角度θ进行检测。已获取的生产过程数据如表2所示，并将车速为ikm/h下的指针偏转角度记作θAi，转速为jr/min下的指针偏转角度记作θDj。

(a)示值补正设备 (b)指针压入设备 (c)视觉检测系统

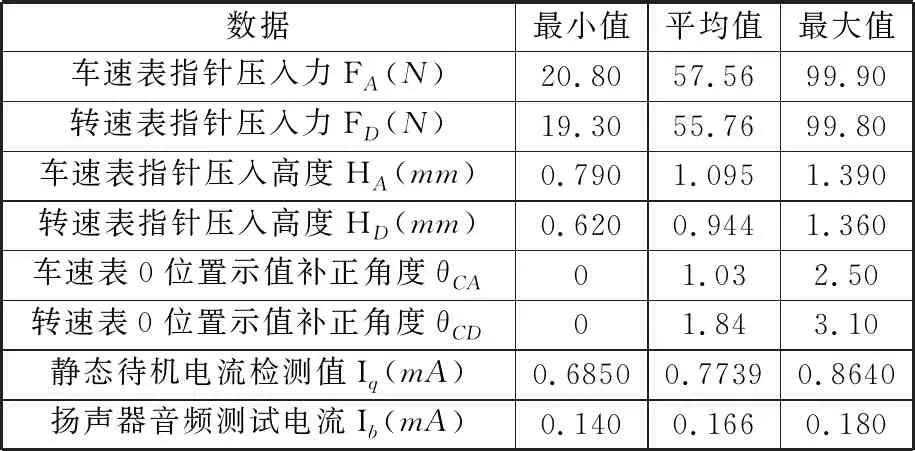
表2 已获取的生产过程数据

3.2 数据集的构建

不同车速/转速下，汽车组合仪表指针偏转的角度直接影响用户读取数值的准确性，决定了产品的组装质量，因此将不同车速/转速下的指针偏转角度作为预测模型的输出。

将仪表组装过程中各表盘指针的压入力和高度、0位置示值的补正值等生产数据作为预测模型的输入。不同组装生产工序中获取的数据量级不尽相同，量级较大的数据会在模型训练过程中占据主导地位，使得偏转角度预测结果对该量级数据的变化非常敏感，为提高模型的预测精度和收敛速度，须对原始数据进行归一化处理。本文采用min-max标准化方法对原始数据进行归一化处理，处理过程如下：

(6)

其中，x为经过归一化处理后的数据，x0为对应的原始数据，x0min、x0max分别为原始数据的最小值和最大值，将x作为各预测模型的输入；[Rdown，Rup]为归一化后的数据区间，本文将其设置为[0.1，0.9]，避免有些机器学习算法在零点处无导数的问题[25]。

3.3 预测模型结构与参数

将2019年3月1日～22日的1400组15B1型仪表产品生产过程数据中的800组数据作为训练集用于模型训练，并将其余600组数据分为3个测试集，以测试平均值来评估模型的预测性能，降低预测结果的不确定性。

为了验证基于CNN-SVR的汽车组合仪表组装质量预测模型的有效性与泛化性，在测试集上使用CNN和SVR算法对仪表指针机能检查结果做出预测，同时与典型回归算法中的线性回归(linear regression，LR)、岭回归(ridge，RG)、随机森林(random forest，RF)算法的预测结果进行对比。

本文使用的预测模型均基于Python语言实现：使用Keras深度学习框架搭建CNN-SVR和CNN模型，使用scikit-learn库搭建其他对比预测模型。如2.1节所述，将CNN-SVR模型设置2个卷积-池化层：卷积核个数分别为32和64，大小为3×3，卷积步长为1×1，激活函数为ReLU；池化层选用最大池化方法，大小为2×2，步长为2×2；最后将全连接层的输出结果作为支持向量回归(SVR)的输入，对指针偏转角度进行预测。根据2.2节，选择SVR的核函数为径向基函数，惩罚函数C和核函数参数σ通过网格搜索(grid search)进行优化[26]。模型训练使用k折交叉验证方法进行参数寻优，本文取k=5。最终得到的CNN-SVR模型详细参数与结构如表3所示。

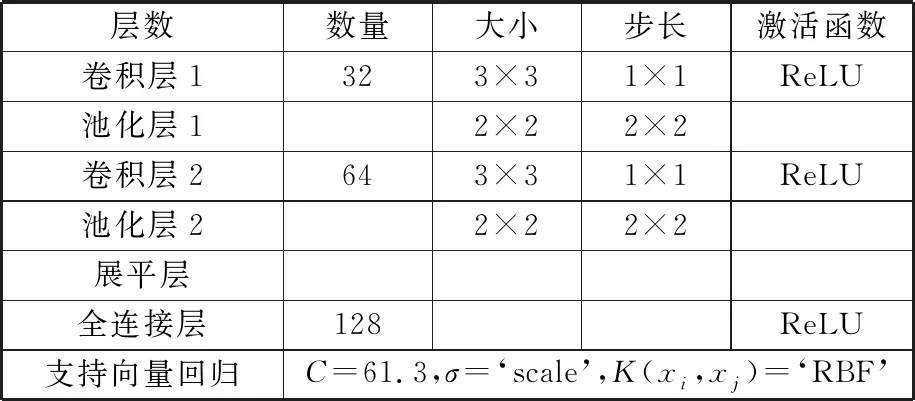
表3 CNN-SVR模型结构与参数

为了与CNN-SVR模型的预测效果进行对比，CNN预测模型的结构参数与其大体保持一致，只是在全连接层之后接入Dropout层，设置丢弃率为0.25；再接入回归层进行预测，激活函数选择linear。

SVR模型的核函数同样选择径向基函数，惩罚函数C和核函数参数σ通过网格搜索进行优化。

线性回归模型通过最小二乘法对数据进行拟合，由于没有使用中心化的数据，拟合后的模型不经过原点，因此设置模型截距为True，同时在构建数据集时已做归一化处理，此处设置归一化为False。

岭回归的正则化系数为2，模型截距为True，使用随机平均梯度下降法(sag)进行迭代。

随机森林学习最大迭代次数为100，特征的评价标准为均方差mse。各模型参数设置如表4所示。

表4 其他预测模型参数设置

3.4 预测结果对比分析

为了准确评价上述模型的预测性能，引入平均绝对误差EMA、均方根误差ERMS、决定系数R2作为模型预测性能的评价指标：

(7)

(8)

(9)

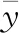
EMA和ERMS直观反映预测值与实际值的偏差，其值越小，模型的预测性能越好；R2用于描述回归模型对因变量随输入变量变化的解释程度，取值范围为(0，1)，数值越接近1，回归模型的可解释性越强，拟合效果越好。

以车速表(车速=40 km/h)功能检查结果为例，对比各模型在测试集上的预测性能。为更直观地对比各模型的预测表现，将预测结果按照车速实际偏转角度排序后绘图，实际偏转角度与测试数据组数并无任何关联。各模型在测试集1上的预测结果如图8所示，取均值后的性能评价指标如表5所示，其中，相对变化量[27]Δe=(emin-ek)/ek表示最小预测误差emin相对误差ek的改变程度，可以看出，CNN-SVR模型的EMA和ERMS均最小而R2最大，说明提出的CNN-SVR模型预测性能最优，模型的有效性得到验证。

(a)CNN-SVR (b)CNN (c)SVR

表5 各模型预测性能评价(车速为40 km/h)

为了进一步验证提出模型的泛化性，以转速表(转速为8000 r/min)功能检查结果为例，对比各模型的预测性能，在测试集1上的预测结果如图9所示，整体性能评价指标如表6所示。

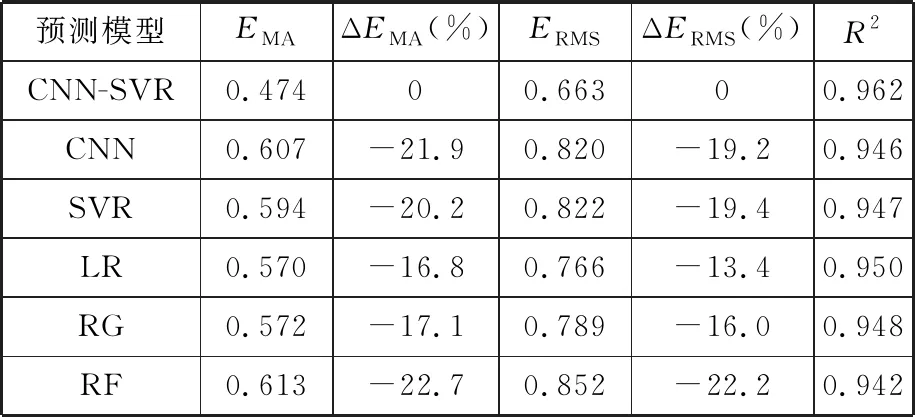
表6 各模型预测性能评价(转速为8000 r/min)

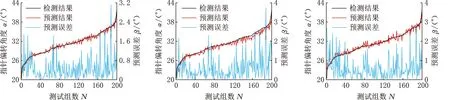
(a)CNN-SVR (b)CNN (c)SVR

对比分析以上案例可得：

(1)在预测有效性方面，各模型预测的误差较小，其中CNN-SVR模型的EMA和ERMS均为最小。在车速40 km/h的功能检查情况下，CNN-SVR模型的EMA和ERMS相比于其他模型至少减小了8%；转速8000 r/min下进行功能检查时，CNN-SVR模型的EMA至少减小了16%，EMSE至少减小了13%，因此CNN-SVR模型是更为准确有效的预测模型。

(2)在模型泛化性方面，CNN-SVR模型在不同案例中的决定系数R2分别为0.949、0.962，模型的可解释性强，拟合效果好。

(3)整体看来，各模型在对偏离平均值较大的指针偏转角度进行预测时的误差相对较大，这可能是组装过程数据的非线性所致；CNN-SVR模型的预测误差在各阶段波动较小即ERMS较小，这得益于CNN在自适应特征提取过程中保留了原始组装过程数据基础信息。

(4)车速表指针偏转角度预测案例中，与转速表案例相比，CNN-SVR模型的EMA和ERMS均减小，预测误差进一步减小，这是因为车速为40 km/h时，指针实际偏转角度波动范围较小(约26°～33)。因此在后续的工作中，还需要针对偏转角度波动范围较大的数据预测结果进行优化。

案例结果表明：本文提出的CNN-SVR模型实现了汽车组合仪表各表盘指针偏转角度的回归预测，其预测的有效性及泛化性比其他预测模型更佳。