钢-玄武岩纤维树脂混凝土结合面法向接触刚度数值计算研究
2022-04-18徐戍廷沈佳兴于英华
徐 平 徐戍廷 沈佳兴,2 于英华
1.辽宁工程技术大学机械工程学院,阜新,1230002.辽宁工程技术大学矿产资源开发利用技术及装备研究院,阜新,123000
0 引言
近年来,我国航空航天、轨道交通、船舶制造、核电等领域发展迅速,进而要求我国机床设备应具有更优越的加工性能[1-3]。玄武岩纤维树脂混凝土(basalt fiber polymer concrete,BFPC)材料是一种高阻尼、热稳定的矿物复合材料,用于制造机床能够有效提高机床减振抗振性能。经过机械加工的BFPC表面是粗糙的[4-5],因此结合面的实际接触面积只是名义接触面积的一部分[6],导致机床中不同零部件间接触表面的接触刚度等性能明显区别于实体材料。对于BFPC机床而言,钢-BFPC结合面的接触性能对整机性能有重要影响,因此研究BFPC机床结合面接触刚度等性能具有重要意义。
采用理论分析结合面接触刚度的核心问题是确定结合面的实际接触面积,结合面的实际接触面积的传统计算方法是通过分形理论计算得到[7-8],但需要确定最大接触点的面积,该面积往往难以获得,给接触刚度的理论计算带来困难。为解决这一问题,本文建立了一种基于离散法的实际接触面积计算方法,并将该方法与结合面接触刚度理论模型结合,建立了一种新的钢-BFPC结合面接触刚度计算方法。
1 钢-BFPC结合面实际接触面积计算
1.1 BFPC试件制造及参数获取
采用实验法获取BFPC材料参数及结合面拓片。玄武岩纤维树脂混凝土是由胶黏剂、骨料、填料以及玄武岩纤维组成。本文所选用的胶黏剂为环氧树脂E44和E51,二者比例为40∶60;骨料为玄武岩碎石骨料,其中骨料颗粒按照粒径大小分为五个等级,玄武岩骨料粒径分别为0.55~0.85 mm、0.85~1.2 mm、1.2~2.5 mm、2.5~5 mm、5~10 mm,质量比分别为7%、10%、20%、56.7%、6.3%;填料为粉煤灰;固化剂为T-31;增韧剂为邻苯二甲酸二丁脂;玄武岩纤维直径为0.015 mm。BFPC的最佳质量配比为:玄武岩矿物骨料80%、粉煤灰填料9%、环氧树脂6.5%、增韧剂1.5%、固化剂2.6%、玄武岩纤维0.4%[8]。采用浇筑的方法制造实验试件,试件为100 mm×100 mm×100 mm的立方体,如图1所示。在BFPC试件的接触表面采用车削的方式进行机械加工,经过机械加工的BFPC表面是粗糙的,如图2所示。

图1 BFPC试件
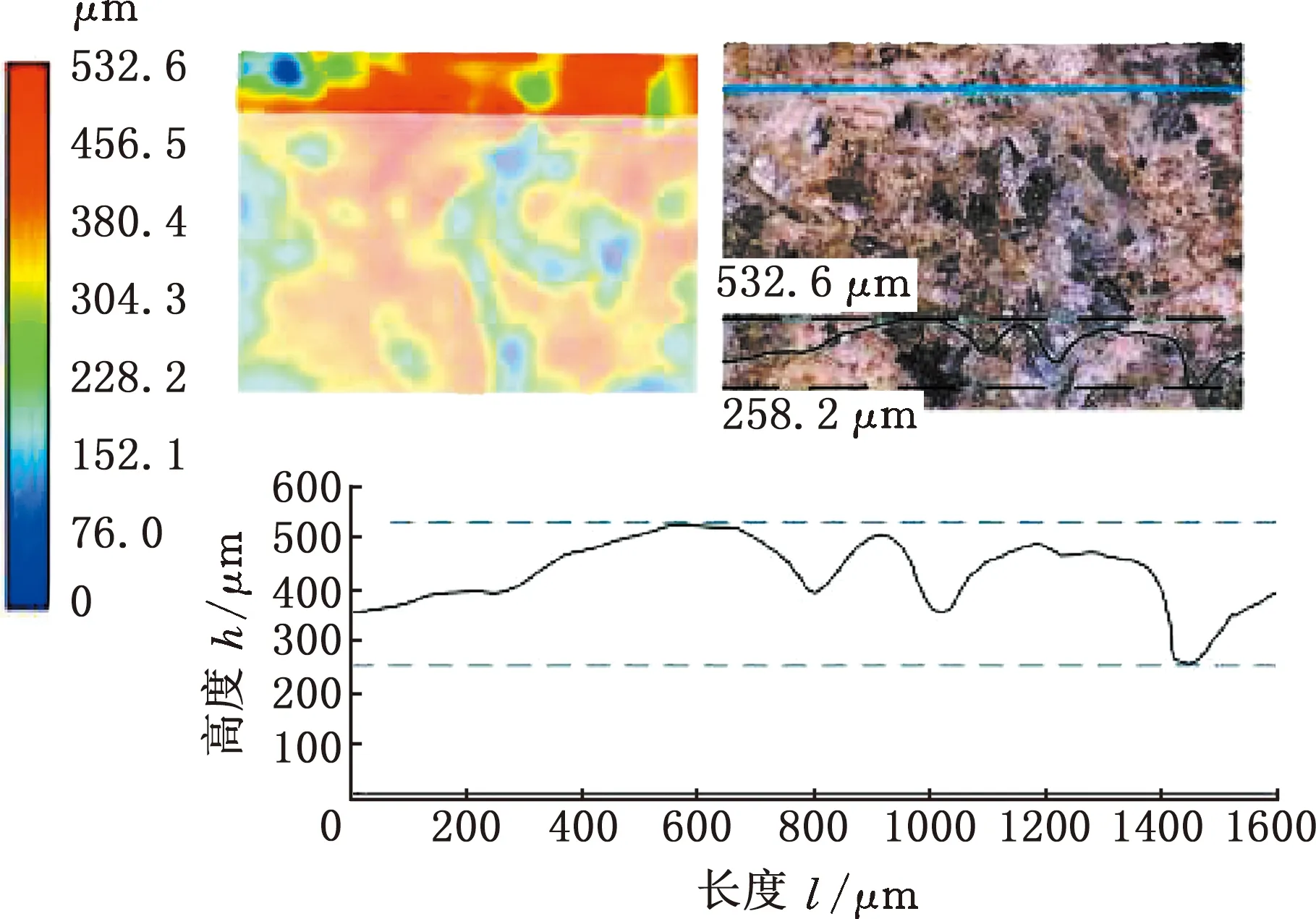
图2 粗糙表面
采用粗糙度测试仪测得试件表面的粗糙度为6.3 μm。将实验试件的机械加工表面涂覆上一层涂料,再通过YAM-2000C微机控制电液伺服压力机分别施加0.2 MPa、0.4 MPa、0.6 MPa、0.8 MPa和1.0 MPa的压力,并保留涂料印记拓片,如图3所示。利用ANS-CMT5205微机控制电子万能试验机以及配备的延伸仪器进行轴向压缩试验,将试件水平放置到液压机的载物台上,调整好其位置,设置液压机的活动压头以0.5 mm/min的加载速度进行加载,与试验机连接的电脑就可直接测得BFPC材料的抗压基本参数,压缩试验如图4所示,钢、BFPC材料基本参数如表1所示。

图3 预载荷为0.8 MPa时BFPC结合面拓片

图4 轴向压缩试验

表1 材料参数
1.2 实际接触面积的离散数值法计算
基于结合面的印记拓片,采用离散法计算实际接触面积。该方法是将钢-BFPC接触面积的问题转化为离散单元类型判断问题[9]。假设目标区域面积共有N2个离散单元,名义接触面积为An,每个离散单元面积为(Δx)2。如图5a所示,离散接触点分为两类:内接触点Ni,该点上、下、左、右相邻点均为接触点;边界接触点Nb,该点上、下、左、右相邻点存在非接触点;其中接触点的数量Na等于内接触点的数量Ni与边界接触点的数量Nb之和。对于数值法,一般认为N→∞时,计算精度最高。假设离散单元数量N2趋于无穷大,则实际接触面积Ar与名义接触面积An之比为
(1)
即
式中,β为接触边界修正系数,0<β<1。
离散单元的接触边界周长ld=MΔx与边界接触点的数量直接相关,其中M是在水平或竖直方向与接触区域相邻的白色格点的边的数量;Δx为离散单元的边长。离散化处理时,为提高计算精度,应将接触区域和非接触区域之间的矩形边界用光滑曲线边界代替,如图5b所示。故接触边界周长ld和平滑边界周长l之间的转化关系为
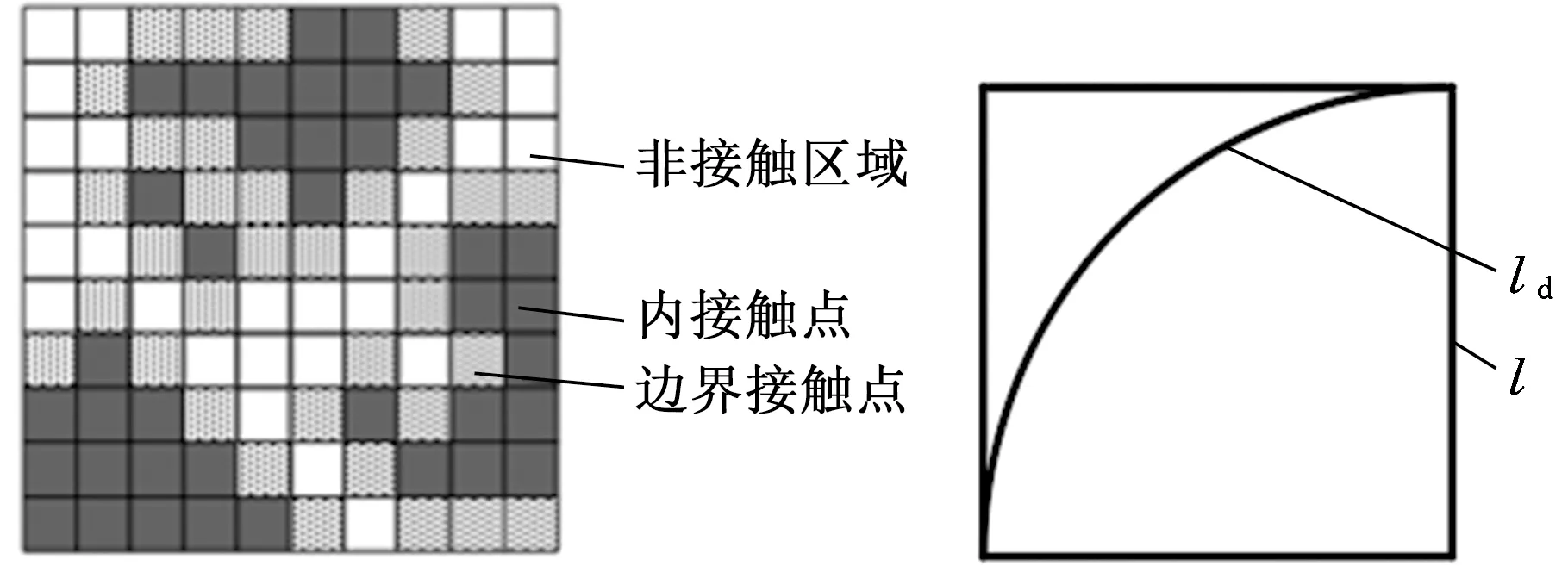
(a)离散化处理 (b)曲线转化
(2)
所以,实际接触面积与名义接触面积之比可按下式估算:
(3)
式中,Aa为离散化后的接触面积。
1.3 接触边界修正系数
对于过渡接触区,假设接触分割线将单个离散单元划分为非接触区和接触区,如图6所示,图中白色区域为非接触区,阴影区域为接触区,A为接触单元内接触面积;t为接触分割线与单元下边线交点到单元格角点的距离;θ为接触分割线与单元边的夹角。有t∈[0,Δx],θ∈[0,π];且假设t与θ均为均匀分布。综上可得
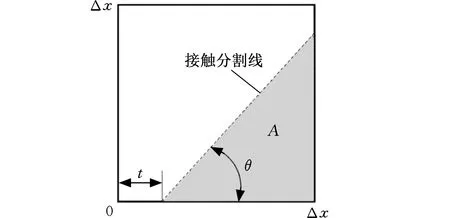
图6 离散单元接触面积
A=
(4)
A(t,θ)函数结果如图7所示,因t与θ均为均匀分布,可以得出针对单个过渡接触单元,A的积分均值即为β:
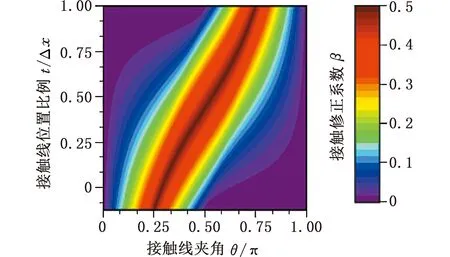
图7 函数彩虹图
(5)
结合式(3)可以进一步得到
Ar≈Aa-0.1181ldΔx
(6)
根据实验获得的结合面拓片,统计出拓片中边界接触点面积和内接触点面积,再根据式(6)计算可得不同面压下结合面实际接触面积。
根据式(6),采用MATLAB软件结合图像判别技术,开发适用于三维粗糙面的接触面积数值分析程序,流程如图8所示。首先将拓片图像导入MATLAB中生成图像矩阵数据,利用程序判别是否为接触位置、哪种接触类型,然后对各种类型的接触点进行统计,最后将数据代入公式求解。
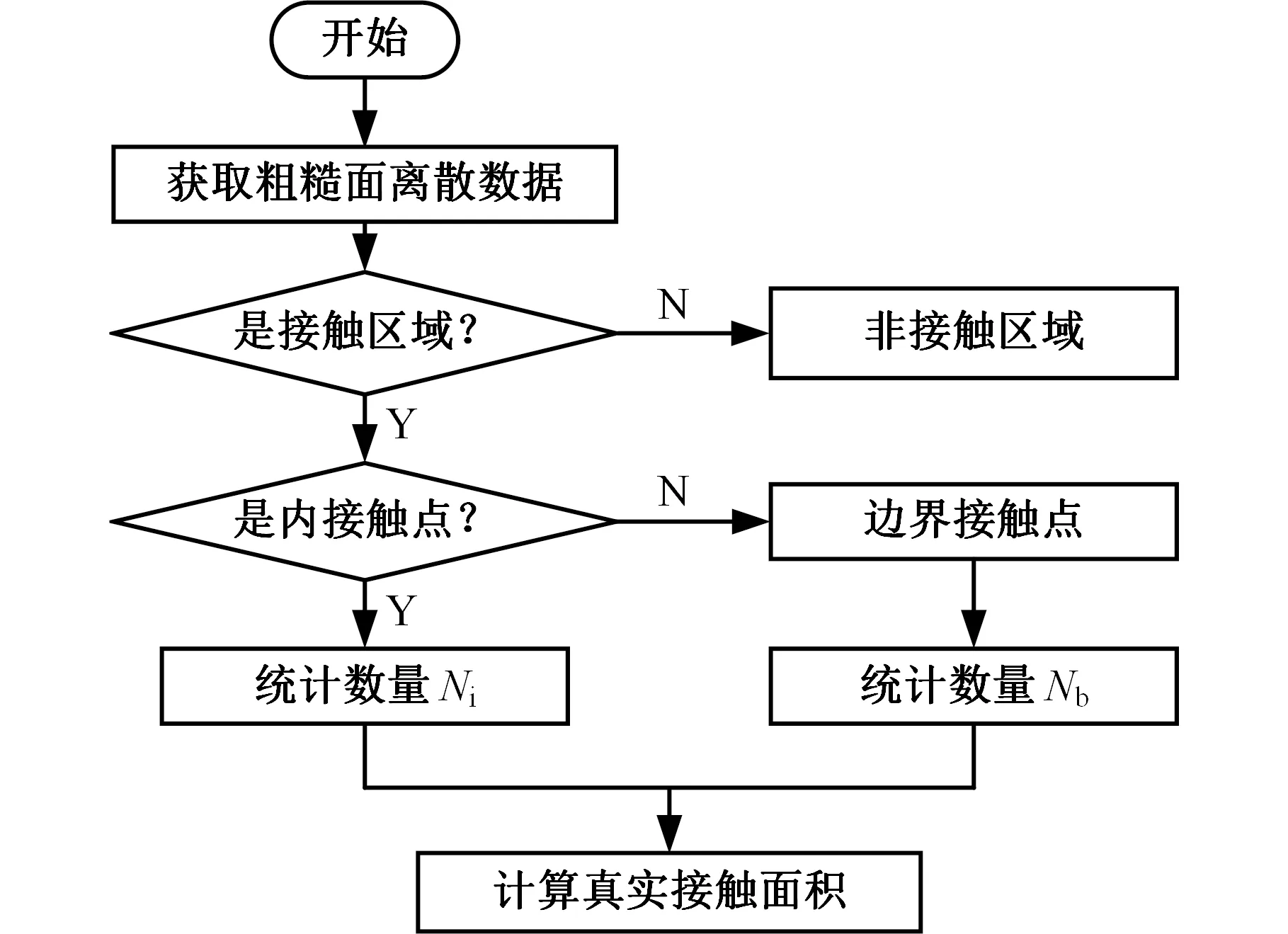
图8 粗糙面接触面积数值分析流程图
分别对接触区域和非接触区域的数据点的个数进行统计,经过统计得到在结合面面压为0.2 MPa、0.4 MPa、0.6 MPa、0.8 MPa和1.0 MPa时的边界接触点数量、内接触点数量以及总的数据点的数量。利用程序计算得到的钢-BFPC结合面实际接触面积如表2所示。
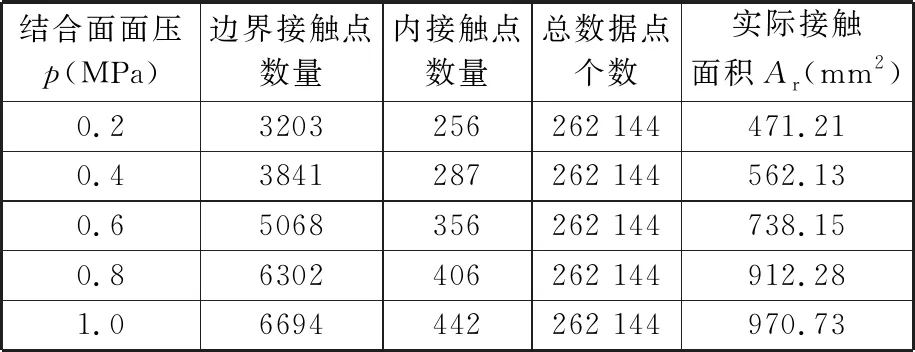
表2 数据点数量统计
根据表2绘制出结合面实际接触面积随法向载荷增大的变化曲线,如图9所示。
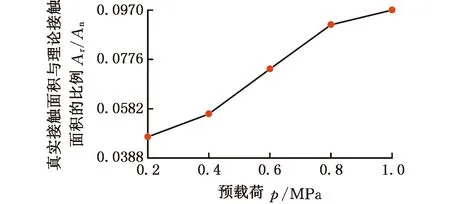
图9 实际接触面积随法向载荷变化曲线
2 结合面的法向接触刚度分形模型
研究表明,经机械加工的人造矿物表面微观轮廓具有分形特征[10],故本节采用分形理论建立粗糙表面的接触模型。通过对地形学的研究,MANDELBROT[11]发现海洋中岛屿的面积分布符合幂函数规律,即
N′(A′>a′)=(a′)-D/2
(7)
式中,N′(A′>a′)为面积A′大于面积a′的岛屿总数量;D为岛屿海岸线的分维。
假设最大接触点的面积为al,数量为1,代入式(7)中,有
(8)
因此接触点的面积分布密度为
(9)
临界接触面积为
(10)
k=H/σyφ=σy/E
式中,H为较软材料的硬度,本文中即BFPC材料的硬度,H=45 MPa;σy为BFPC材料的屈服强度;E为复合弹性模量[12];G为特征长度尺度参数。
当BFPC和金属形成结合面时,可以视作粗糙表面和刚性平滑表面相接触,如图10a所示。对于粗糙表面上的单个微凸体,可以将其近似等效为球体,等效曲率半径为R。当球体在法向载荷作用下与刚性平滑平面保持接触时,将产生法向接触变形δ,接触状态如图10b所示[13]。
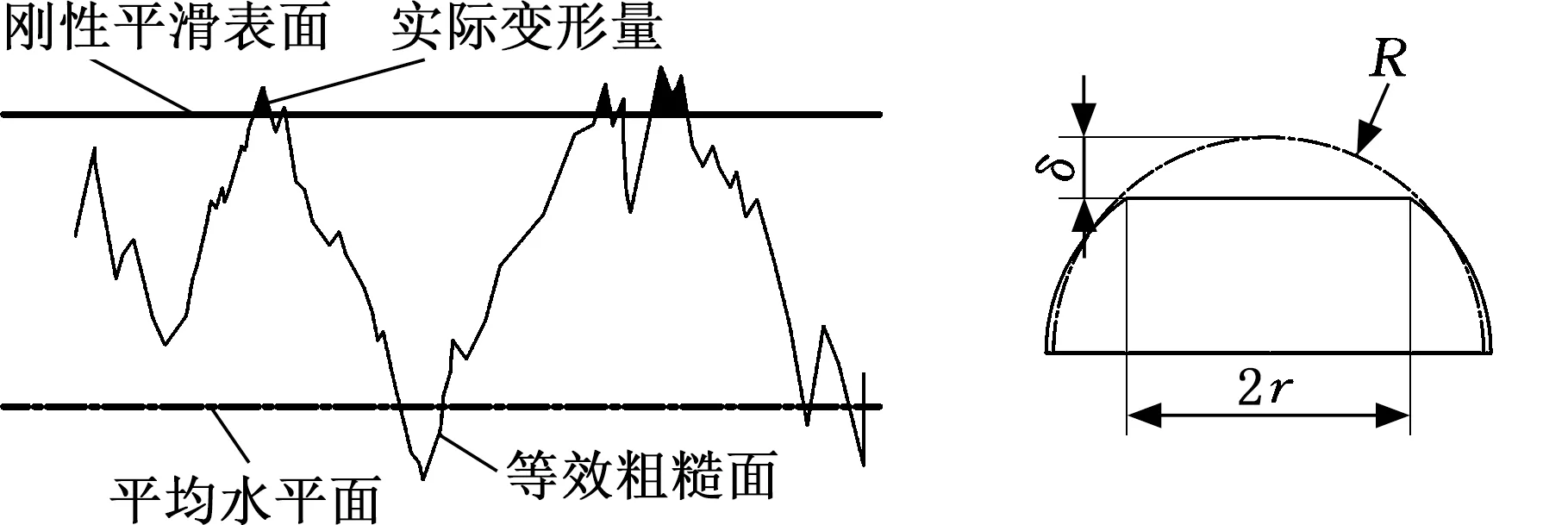
(a)接触示意图(b)微凸体接触状态
若接触区域半径为r,则有
(11)
(12)
(13)
式中,p′为微凸体上的法向载荷;δ为法向接触变形;E1、E2和ν1、ν2分别为钢和BFPC材料的弹性模量和泊松比。
根据式(11)和式(12),单个微凸体与平面接触的法向接触刚度kn可以由下式表示:
kn=2Er
(14)
由于接触区域的接触面积a可以表示为
永磁同步电机矢量控制实验系统调试及故障分 析 ………………………………………… 徐 婷,戴 怡(27)
a=πr2
(15)
于是有
(16)
假设粗糙表面上各微凸体之间的相互作用忽略不计[14],则结合面法向接触刚度可由下式计算:
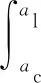
(17)
将式(16)、式(9)代入式(17)得
(18)
整理得
(19)
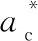
(20)
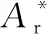
对图2所示的实验试件利用图11所示NANOVEAP550非接触式三维表面形貌测试仪观测表面形貌,得到粗糙表面的分形参数D=1.169,G=2.78×10-13。
图11 微观形貌数据采集实验现场图
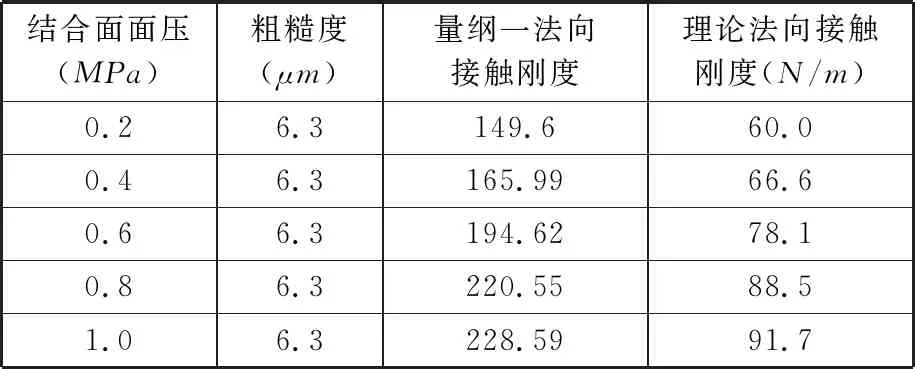
表3 法向接触刚度理论计算
3 实验验证
本实验通过测定钢-BFPC结合面固有频率来推导出结合面刚度。钢和BFPC试件受到法向载荷作用挤压形成结合面,如图12a所示。结合面刚度由结合面间相互接触的微凸体的接触特性决定,每一组相互接触的微凸体都可视为一组弹簧阻尼单元,因此钢-BFPC结合面模型可以表示为图12b的理论模型。
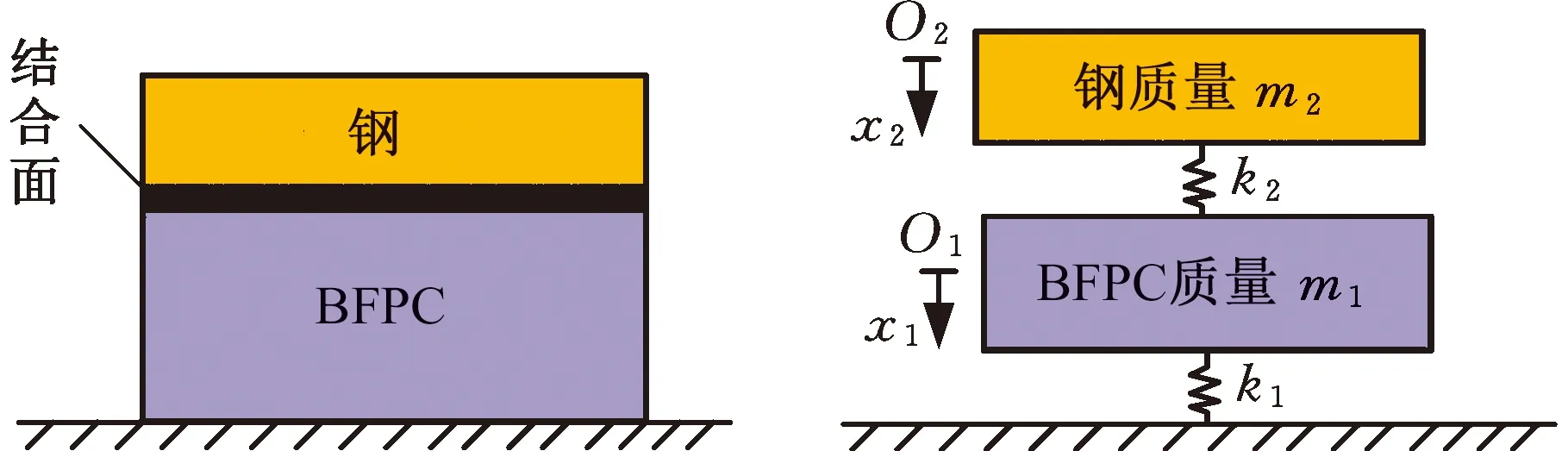
(a)组件结合面示意图 (b)等效动力学模型
通过电子秤测得BFPC试件的质量为m1,设BFPC试件自身与地面接触形成的总刚度为k1;钢试件的质量为m2,因为钢试件的刚度远大于钢-BFPC结合面的接触刚度,故忽略钢试件的刚度,设钢-BFPC结合面刚度为k2。由机械系统动力学可知,阻尼对系统固有频率影响较小,因此忽略其影响,将此模型看作两自由度无阻尼自由振动系统。根据图12b可得钢-BFPC试件的振动微分方程:
(21)
式(21)的特征方程为
(22)
k11=k1+k2k12=k21=-k2k22=k2
式中,ωn为系统角频率。
展开此行列式得
(23)
(24)
式中,f为系统频率;K为系统刚度;m为系统质量。
所以,通过实验测得式(23)中的ωn、m1、m2后即可求得钢-BFPC结合面刚度k2。
采用力锤激振系统测试钢-BFPC结合面的法向接触刚度,实验原理如图13所示。首先通过力锤对钢试件施加一个法向的脉冲激励,两个加速度传感器分别用于检测钢试件和BFPC试件的振动曲线,将加速度传感器检测的实时数据传递到DH5922N动态信号测试系统中进行记录,最后在计算机终端对数据进行处理。实验装置如图14所示。应用锤击法对试件进行激振,当结合面的面压为0.4 MPa时组件的模态响应测试结果如图15所示。
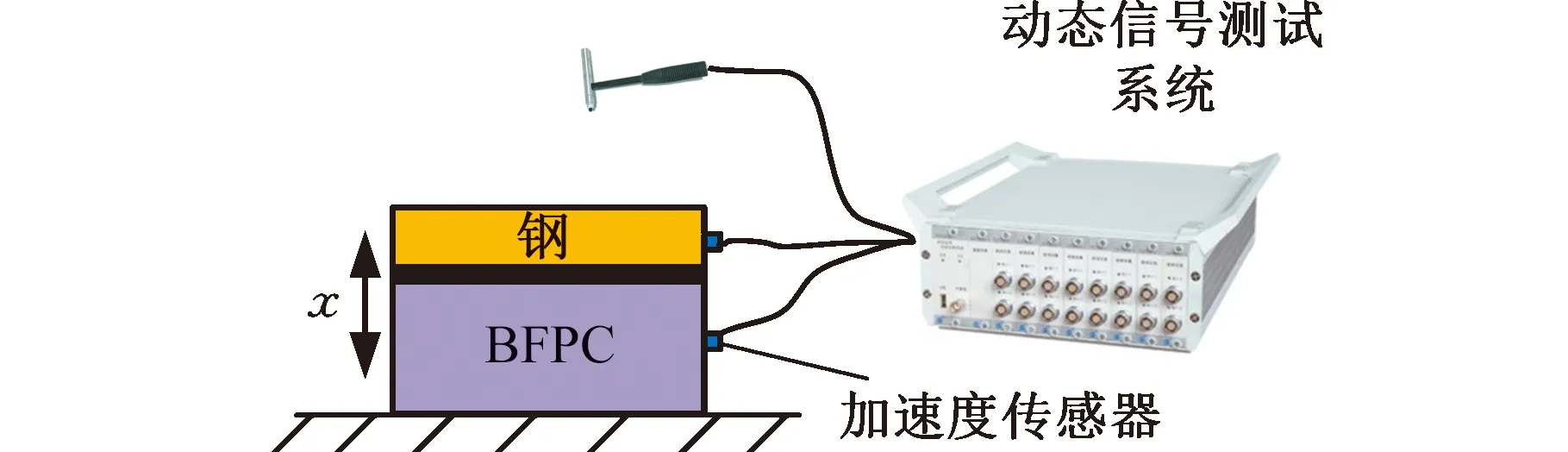
图13 实验原理示意图

图14 结合面实验实物图
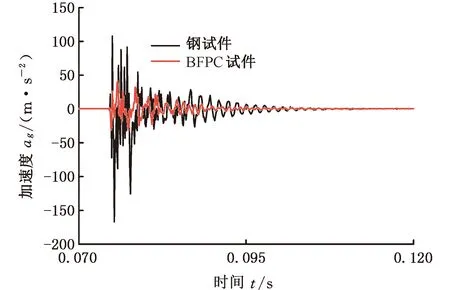
图15 预载为0.4 MPa时的振动曲线
根据实验测得的数据利用MATLAB软件求解式(23),得到钢-BFPC结合面刚度k2,然后通过实验测得不同面压时的振动曲线,再通过同样方法计算不同面压时的钢-BFPC结合面刚度,结果见表4。根据式(20)中理论计算的量纲一结合面法向接触刚度与有量纲接触刚度的关系,推导出有量纲的理论法向接触刚度,结果见表4。因为二者皆为同单位制下的刚度所以具有可比性,对比得到图16所示的法向接触刚度与接触载荷之间的关系。
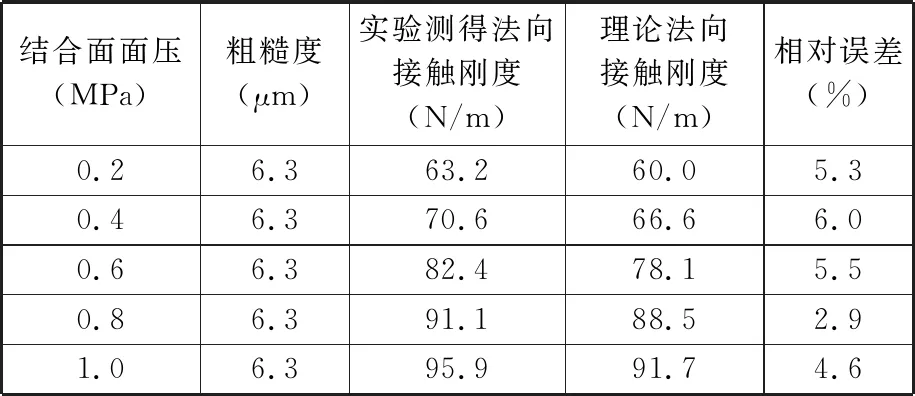
表4 结合面法向接触刚度实验数据
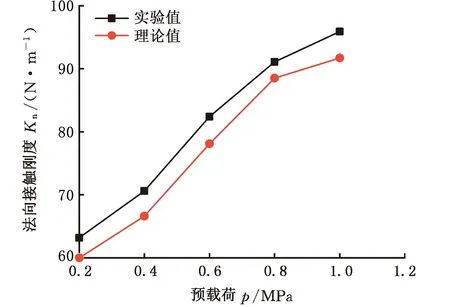
图16 预载荷对结合面刚度的影响规律
由表4和图16可以发现,结合面法向接触刚度随着预载荷的增大而增大。这是因为随着法向载荷的增大,结合面间的实际弹性接触面积增大。理论值和实验值之间的误差来源主要有两点:①在获得结合面拓片的过程中,由于人为因素与环境因素的干扰,导致获取的拓片不准确,比实际的接触面积小;②在对试件施加预载荷时,预载荷的大小存在一定误差,导致获取的拓片不能很好地反映实际接触面积。通过理论计算和实验得到的不同预载荷下钢-BFPC结合面刚度的相对误差均小于6.0%。
4 结论
(1)提出了一种计算结合面实际接触面积的新方法,并通过MATLAB软件与粗糙面三维数据开发了适用于三维粗糙表面的接触面积数值分析程序,计算得到在结合面面压为0.2 MPa、0.4 MPa、0.6 MPa、0.8 MPa和1.0 MPa时钢-BFPC结合面的实际接触面积分别为471.21、562.13、738.15、912.28、970.73 mm2。
(2)将实际接触面积计算方法与结合面分形接触刚度理论结合,得到新的结合面接触刚度计算模型,并通过实验检验理论结果,得到实验和理论两种方法的相对误差均小于6.0%,证明了该计算方法的正确性和有效性。
