基于混合回归模型的沿海平原河网洪水位预报研究

周 焕，闪丽洁，揭梦璇，汤 斌

（浙江省水利水电勘测设计院，浙江 杭州 310002）

1 研究背景

浙江省位于我国东南沿海、太平洋西岸的亚热带季风区，是一个洪涝台灾害易发多发的地区。东部沿海平原既是浙江省经济发展主导地区，也是人口和生产力要素聚集区，多处在河流中下游，背山滨海，上承山洪，下受潮汐顶托，地势低平，排水不畅。近年来，极端天气多发，风、暴、潮不利组合几率增加，竞赛式圩区建设导致外江洪水位不断抬升，加上部分区域地面沉降、入海排水口门外延等诸多因素，造成平原排涝形势“雪上加霜”，对平原感潮河网城市防洪排涝工作带来巨大的挑战［1-3］。

平原感潮河网城市防洪排涝的关键在于控制市区境内主要河道的水位。相比于山区的单一或树状河道，平原河网水文条件错综复杂，由此带来预报模型的方程组离散和求解更加困难，这是多年来人们研究河网问题的难点［4］。以往研究中，主要采用水动力模型，涉及控制方程组简化、方程组离散和求解、初边条件确定等一系列问题［5-7］。此类方法需要详细的河道地形资料及特征参数，且计算收敛稳定性受输入边界影响较大，规模庞大、时间长。近年来随着物联网技术的发展和数据感知技术的成熟，多元逐步回归模型、人工神经网络模型等基于大数据的数理统计方法快速发展，在气象、水文等方面得到了大量的应用［8-11］。都宏博［12］采用门限回归和BP人工神经网络模型建立了感潮河段水位预报模型，结果表明构建模型比较符合感潮河段水位变化的物理规律，适用于长江流域感潮河段水位预报。王竹等［13］将智能算法与半分布式水文模型相结合，构建了一种半分布式BP神经网络模型，并应用在辽宁省大伙房水库洪水预报工作中，取得了理想的预报效果。然而数理统计方法在平原河网洪水预报工作中应用较少。

本文以浙江沿海温瑞平原的9个特征断面为研究对象，以各断面2005年5号“海棠”台风、2007年13号“韦帕”台风、2009年8号“莫拉克”台风、2013年23号“菲特”台风等6场洪水过程为依据，尝试采用在水文产汇流预报模拟成果的基础上利用数理统计方法解决问题的思路，利用产汇流模型计算求得各水文分区洪水过程，与下游潮位过程一起形成预报因子库，并在此基础上针对各特征断面构建相应的混合回归模型，从而进行温瑞平原洪水位预报研究。

2 研究流域和数据资料

温瑞平原是浙江省东南沿海瓯江和飞云江之间多块平原的总称。温瑞平原总集水面积948 km2。地形总体上西部及西南部为山区、东部为平原，北临瓯江、南界飞云江、东濒东海，地理位置如图1所示。区域整体地形呈西高东低，山区无调蓄水库、山脚无集水沟，上游洪水直接排入城区或低地，城区易成为上游周边山区和较高地势来水的蓄水区［14］。平原河网水系分布较密，其中主要水系为温瑞塘河，北起温州，南至瑞安市城区，是沟通瓯江、飞云江两大水系的主要内河［15］。

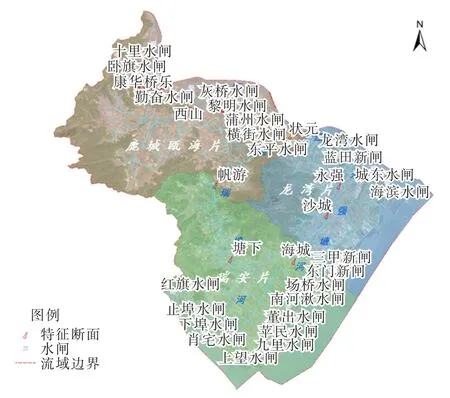
图1 温瑞平原流域分布图

经分析得知，温瑞平原排涝格局为向北排瓯江、向南排飞云江、向东排东海。为了更加准确地模拟特征断面水位，本文根据平原河网内水的排流情况，将温瑞平原流域划分为3个片区，分别为鹿城瓯海片、龙湾片和瑞安片，并对不同片区内的断面水位分别进行模拟。所选择的率定期为1999年9月3日—6日、2005年7月18日—21日、2007年9月18日—21日和2009年8月7日—10日共4场洪水，检验期为2010年7月24日—27日和2013年10月6日—9日共2场洪水。所用的资料包括6场洪水对应的流域内雨量站降雨资料、9个特征断面水位资料、临海闸门闸前水位资料、闸门参数资料以及瑞安站潮位资料等，时间尺度为小时。

3 研究方法

与山区型河道汇流速度快、汇流方向单一的特点不同，温瑞平原地势平坦，水系四通八达，特征断面洪水过程很大程度受周围片区水位变化的影响，因此平原地区洪水位预报更加复杂。参考传统的水动力模型如MIKE11的建模思路，首先对整个温瑞水系区域河道现状水力条件进行分析，结合水文站和雨量站分布划分为子流域，建立产汇流模型模拟各子流域的降雨径流过程，作为温瑞平原混合回归模型的预报因子库，并在此基础上构建混合回归模型，即首先分别构建门限回归模型和多元逐步回归模型，再采用多元线性回归模型进行集合预报，从而实现对温瑞平原洪水预报工作。

3.1 水文分区产汇流模型构建 根据流域特性将研究区域划分多个水文分区，根据站点观测的雨量计算各水文分区的流量过程，为混合回归综合模型提供预报因子库。依据河流水系、分水岭及下垫面情况等要素，本研究区域可细化39个山区分区和91个平原分区。采用泰森多边形法由8个雨量站点的雨量加权计算得到各分区的面雨量，再分别对山区和平原分区采用不同的模型计算产汇流过程。各分区边界范围如图2所示。

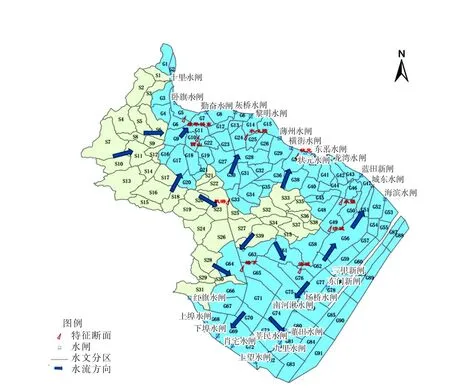
图2 研究区域水文分区图

山区分区采用蓄满产流模型进行产流计算，后根据分区集水面积大小，选用不同的计算方法，集水面积大于50 km2的采用瞬时单位线法，小于50 km2的采用“浙江省推理公式法”，具体计算方法参考论文［16］。平原分区按不同地类分别推算产水过程：水面按水量平衡方程由降雨扣除水面蒸发推求产水量；水田由降雨扣除水稻蒸腾及水田下渗并考虑水田最大持水深度推求产水量；旱地根据前期土壤含水量由降雨扣除一定的损失及下渗，并考虑旱地最大持水深度从而推求产水量；其他建成区则采用径流系数法由降雨推求产流过程。

3.2 预报因子的确定 预报因子筛选准确、全面与否，是对准确模拟洪水位工作的前提［17］。结合流域地理、气候、洪水特征等特点，采取物理成因分析与数理统计分析相结合的思路，从对洪水过程的贡献率、影响程度及其获取难易程度等方面综合考虑，识别洪水位的主要影响因子，为模型构建奠定必要的基础［18-19］。

为了得到更为合理准确的预报因子组合，本文采用相关系数与逐步回归耦合的方法分两步进行筛选工作［20］。首先选取足够数量的影响因子作为预报因子库，在成因分析的基础上分析洪水来源，同时分析特征断面周围的其他影响因素。其次，采用相关系数法从预报因子库中筛选出与断面洪水位过程相关性较强的因子，作为待选预报因子组合。最后，通过逐步回归模型对待选因子进一步筛选，得到最终的预报因子组合，作为混合回归模型的输入项进行洪水位预报。

3.3 混合回归模型构建 混合回归模型是在模拟洪水变化过程寻求相关链接因子的一种自适应统计学技术，主要由门限回归模型和多元逐步回归模型组成，思路为分别构建门限回归模型和多元逐步回归模型，并在此基础上采用多元线性回归法建立集合预报模型。

3.3.1 门限回归模型 门限回归模型由英籍华人H.Tong（汤家豪）博士首创提出，将传统的全局线性逼近分成几段进行线性回归逼近，分割由“门限”变量来控制［21-22］。其实质上是把预报问题按状态空间的取值进行分类，用分段的线性回归模式来描述总体非线性预报问题［23］。本文采用二分割门限回归模型，将待模拟洪水位序列及其它预报因子序列按最优分割点分为两段，分别进行多元回归计算。门限回归模型可表示为：

3.3.2 多元逐步回归模型 多元逐步回归模型是在多元线性回归分析的基础上派生的一种建立最优多元线性回归方程的算法技巧，核心是利用求解求逆紧凑变化法和双检验法，从大量因子中选择重要有效的因子建立最优回归方程［24］。目前，我国广泛应用的逐步回归算法，其实质是用高斯-亚当消去法解正规方程式，巧妙地把选取重要因子的思想结合进去，大大提高了计算效率［17］。

3.4 评价指标 本文所采用的洪水预报精度评定项目包括洪峰水位、洪峰水位出现时间和洪水过程。选择确定性系数Dc和合格率QR为洪水预报精度评价指标。依据《水文情报设计规范》中定义，计算公式如下：

4 结果与分析

4.1 预报因子筛选 首先，在成因分析的基础上分析洪水来源。温瑞平原洪水受上游山区洪水下泄、区间暴雨和下游潮位顶托的共同影响。其中上游山区洪水下泄、区间暴雨均可通过产汇流模型计算各分区产汇流过程进行体现。另外，温瑞平原沿海地区分布较多挡潮闸和排（退）水闸，为了在排洪水的同时防止潮水倒灌，闸门会随着外海潮位的涨落而不断启闭，闸上水位亦会随之发生变化。通过分析发现，康华侨东、西山、水心殿、状元等断面洪水过程均会不同程度受到沿海闸门启闭的影响，因此断面附近闸门闸上水位亦可作为预报因子，与各水文分区产汇流过程共同形成预报因子库。其次，通过相关系数法逐时计算因子与洪水位序列的相关系数，选出相关系数绝对值最大的10～15个因子为待选预报因子。最后，通过逐步回归模型对待选因子进一步筛选，得到最终的预报因子组合，作为混合回归模型的输入项进行洪水位预报。

需要注意的是，闸上水位过程需要通过堰流公式计算得出。首先根据流域实际情况，汇总水文边界入分区产流过程，对区域总流量过程进行模拟，并根据各闸门大小以及所处位置，模拟出总流量过程对各闸口断面流量的分配关系，从而进一步得到各闸口断面的流量过程。模型将闸门处至闸上断面间的河道概化为一个水库，依据水量平衡原理，采用堰流流量公式计算下泄水量和闸上水位过程。为了更加精确地模拟闸前水位和断面入流过程的变化，将时间尺度由1 h缩短至15 s，对应的流量过程和下边界潮位过程由插值所得。

结合温瑞平原各断面的地理位置、洪水来源等因素，最终筛选出的预报因子组合如表1所示。可以看出，西山、康华侨东和水心殿断面与勤奋水闸较近，断面水位过程与勤奋闸的闸前水位过程存在较大的相关性；永强和沙城断面与蓝天水闸接近，断面水位过程与蓝天水闸的闸前水位存在较大的相关性；帆游、塘下和海城断面离下边界水闸距离较远，需直接与各分区产汇流过程建立相关性求得。因此不同断面的洪水位过程需采用不同的因子组合进行模拟。

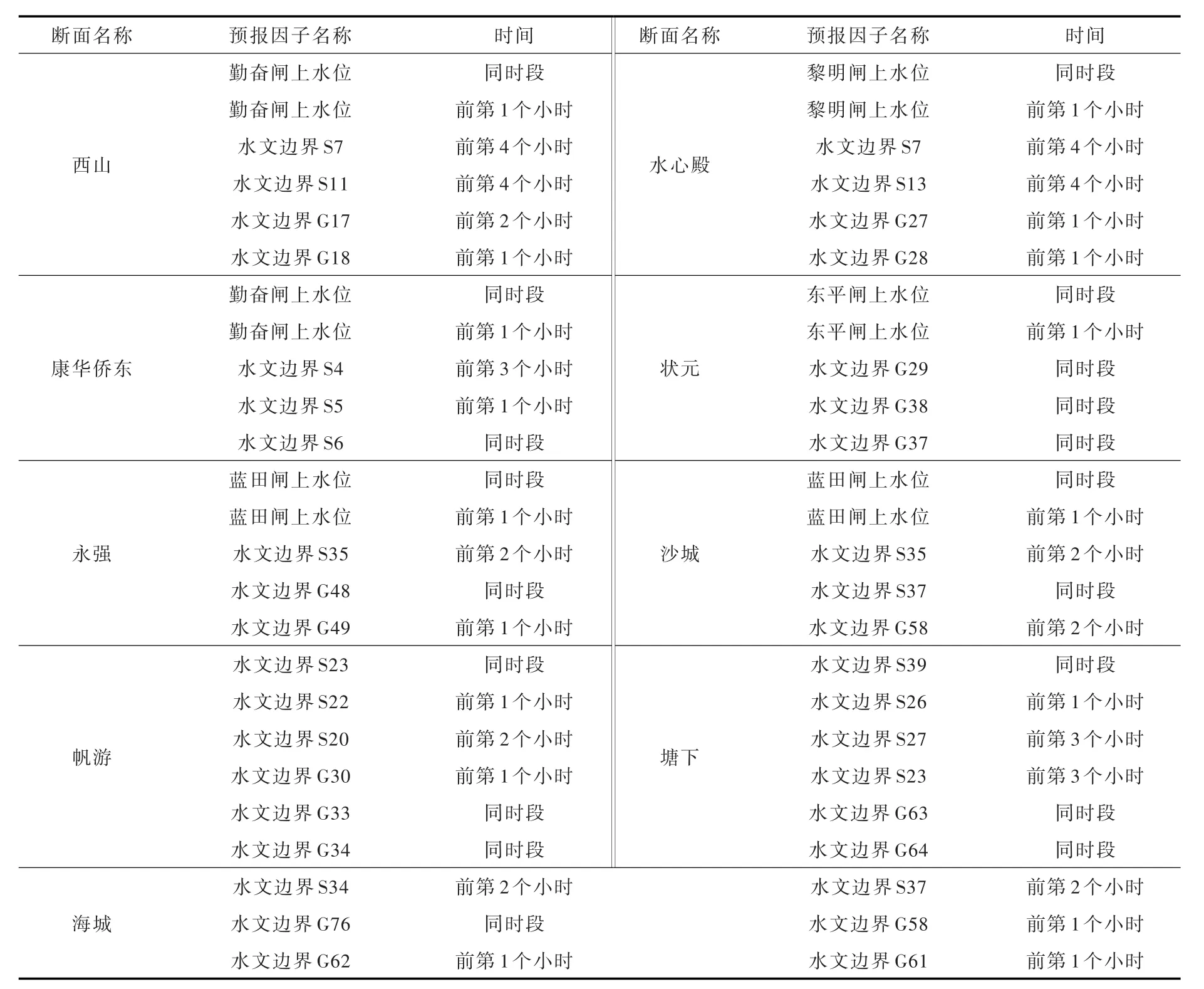
表1 温瑞平原流域各断面水位预报因子筛选结果

4.2 洪水位预报结果分析 基于筛选出的预报因子组合，构建混合回归模型。采用1999年9月3日—6日、2005年7月18日—21日、2007年9月18日—21日和2009年8月7日—10日共4场洪水作为率定期训练模型参数，对2010年7月24日—27日和2013年10月6日—9日对应的9个断面的洪水位进行预报研究。通过对比发现，西山与水心殿断面洪水过程相似。这是由于西山与水心殿断面距离较近，同处于北排瓯江的格局片区，河网水系连通，且洪水来源相同。永强和沙城断面、帆游和塘下断面也存在上述情况。由此可以得出，当进行沿海平原河网洪水预报工作时，可先结合洪水来源与排水走向，分析平原河网排涝格局，在此基础上合理布置特征断面，对其分别构建混合回归模型，即可快速模拟出整个平原的洪水位空间分布及洪水演进情况。

为节省篇幅，本文分别从各片区中选择一个代表站，以康华侨东、永强和塘下端面为例，对比六个场次洪水的实测与模拟过程，如图3所示。可以看出，在率定期，3个代表站水位的模拟值与实测值演变趋势相同，且对水位峰值出现时间和峰值大小模拟效果较好，其中2009年模拟效果最好；但对低水位及退水段模拟不佳，尤其是1999年，低水位时模拟值偏大，水位发生波动时的波谷值模拟也偏大，有待改进。

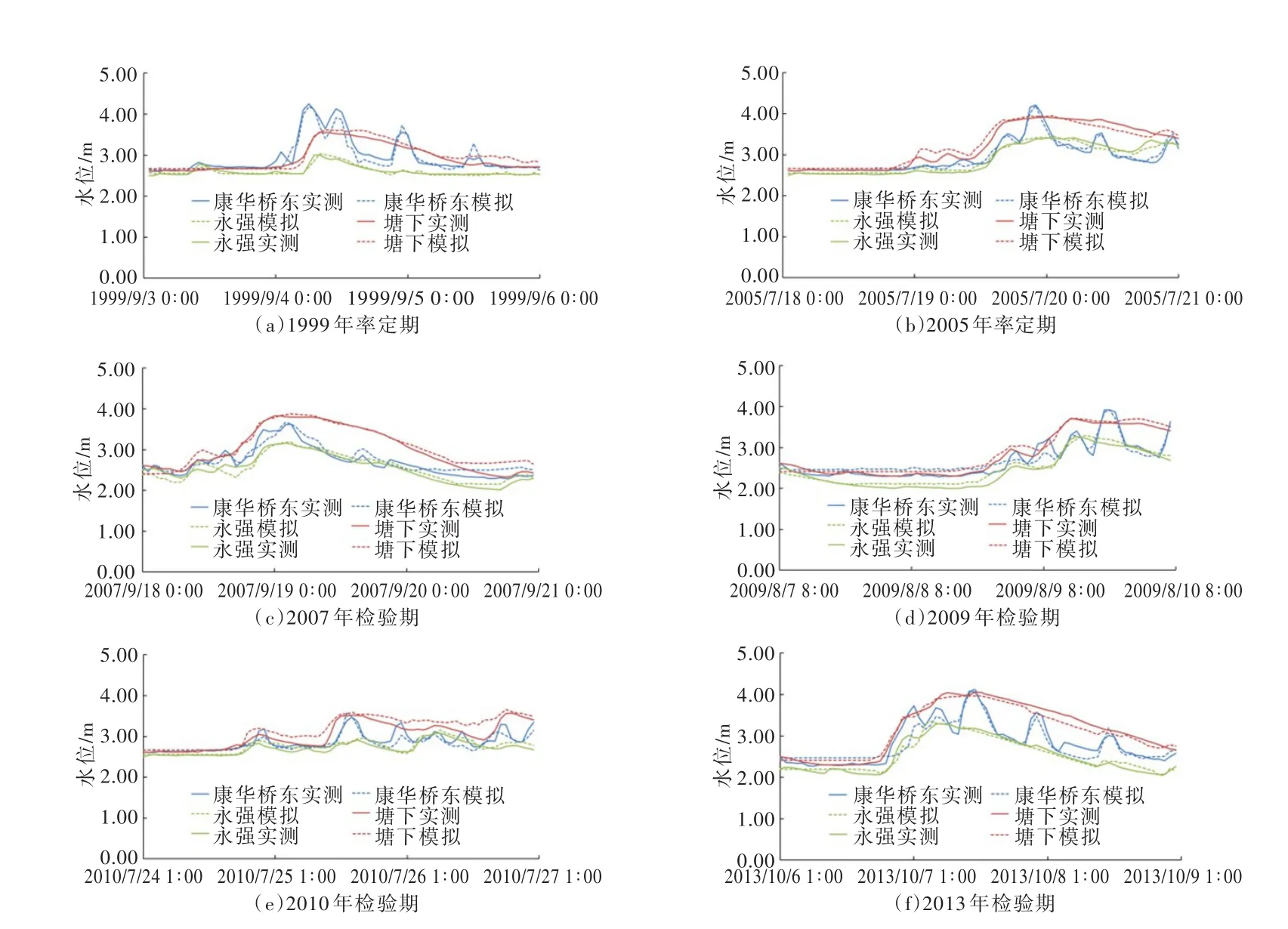
图3 温瑞平原特征断面洪水位实测与模拟对比过程图

为了更进一步评价模型的准确性，本文统计了每个特征断面每场洪水的特征值进行精度评价，本研究选取的预报精度评价指标为确定性系数（Dc）和平均合格率（QR），统计结果如表2所示。可以看出，洪峰水位计算值普遍比实际值偏大，但其差值小于0.10 m；峰现时间错时基本介于3 h以内；确定性系数均大于0.70，部分洪水场次确定性系数甚至高达0.97；合格率基本高于70%，预报效果整体较好。

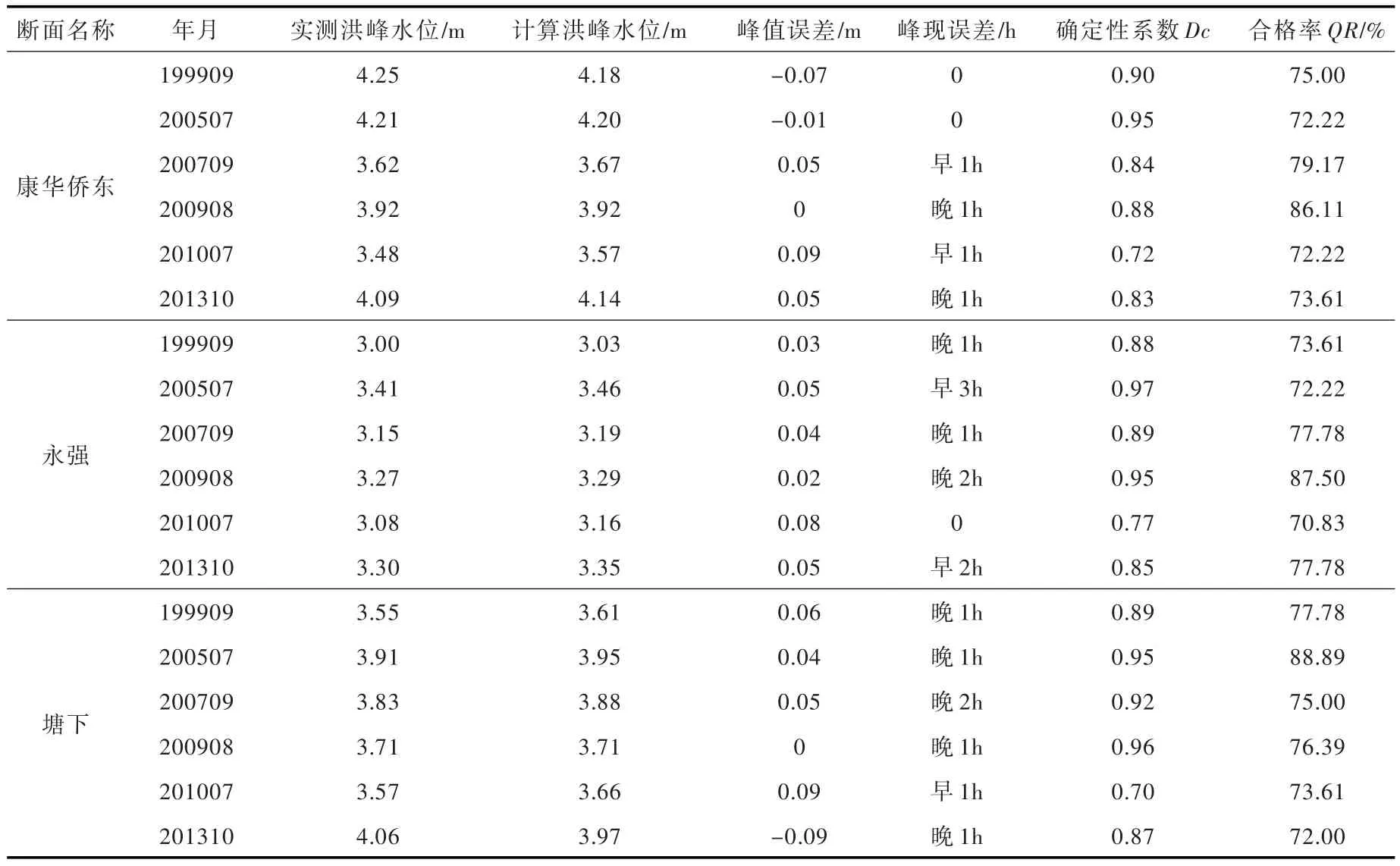
表2 混合回归模型洪水位计算结果

针对温瑞平原9个特征断面率定期和检验期分别进行精度评价，评价结果详见表3。可以看出，率定期的平均确定性系数为0.92，检验期为0.82，均处于0.80以上；率定期的平均合格率达80.71%，检验期平均合格率为75.60%，预报精度整体较高。从预报成果来说，采用混合回归模型进行洪水位模拟满足《水文情报预报规范》（GB/T 22482-2008）中规定的乙级预报精度标准，即合格率QR介于70.0%～85.0%，确定性系数Dc介于0.70～0.90，效果良好，可用于作业预报。

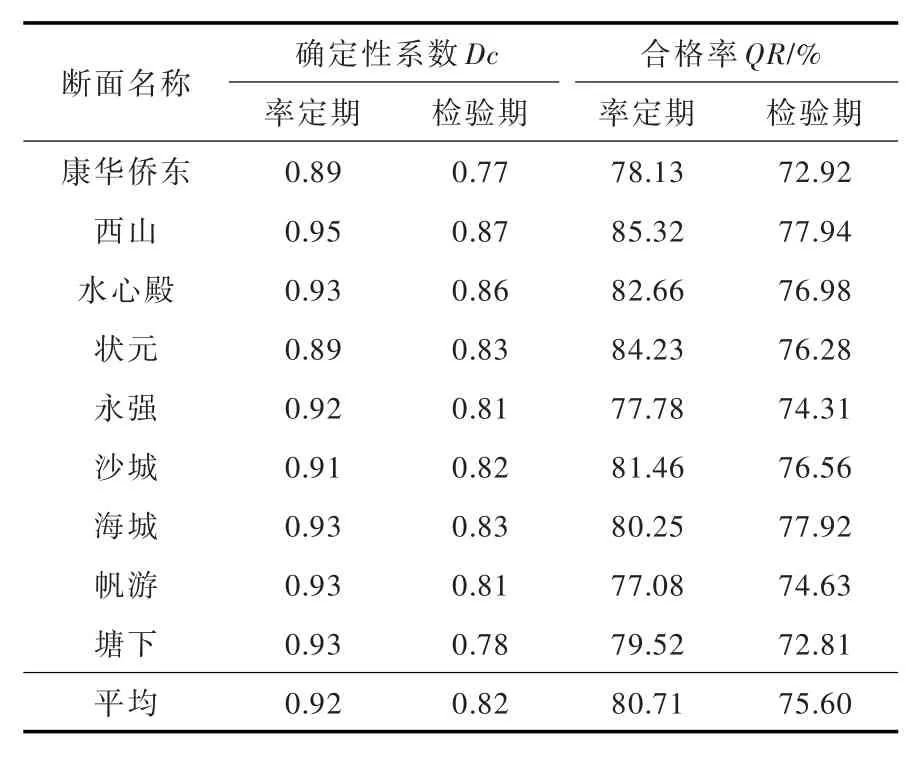
表3 混合回归模型洪水位计算精度评价

值得注意的是，从图3可以看出，康华侨东断面洪水位过程并不像山区河道具有明显的涨水段、退水段，而是波动剧烈，除了明显的峰值之外，还存在周期性的波动情况。这是由于康华侨东断面距离闸门很近，其水位受洪水与潮水双重作用的影响。结合其他断面水位过程得知，距离闸门越近，水位受闸门启闭影响越大，波动越剧烈。说明在进行沿海平原河网洪水预报研究时，潮位顶托和闸门控制是不可忽视的影响。

5 结论与建议

本文以温瑞平原流域为例，采取物理成因与数理统计分析相结合的思路对沿海平原河网洪水位预报工作进行研究，得到结论如下：

（1）根据平原河网洪水过程的时空变化特征，通过利用产汇流模型计算求得各水文分区洪水过程，与下游潮位水位过程一起形成预报因子库，并在此基础上针对各特征断面构建相应的混合回归模型。此方法思路清晰，计算简单，运行稳定，可为平原感潮河网洪水位预报提供一条有别于传统洪水预报模式的快速建模途径。

（2）利用2010年和2013年2场洪水的实测资料，对模型进行验证。结果表明，验证洪水模拟值与实测值演变趋势相同，且对水位峰值出现时间和峰值大小模拟效果较好，确定性系数为0.82，合格率为75.60%，预报精度较高。混合回归模型在温瑞平原河网洪水位预报中可以取得较好的效果。

（3）模型仍存在一定的优化空间。例如，若河网中建有闸、堰等水工建筑物，在筛选因子和构建模型时，还应考虑水工建筑物对洪水的调蓄影响；在预报模型对低水位及退水段模拟不佳的问题上，可尝试将洪水过程分段考虑，分别针对高水位和低水位进行预报因子筛选和混合回归模型构建工作。另外，混合回归模型的预测精度与输入的历史数据量有关，历史洪水样本越多，模型参数越向最优值靠近，因此在实际预报工作中，还需考虑实现模型的自我学习功能，这些有待日后的研究。