基于黏菌算法的热电联产机组负荷优化分配
2022-04-18卫治廷周兴野盛德仁
卫治廷,张 敏,周兴野,李 培,盛德仁,李 蔚
(1. 浙江大学 能源工程学院,杭州 310027;2. 中电投东北能源科技有限公司,沈阳 110179)
目前,我国燃煤机组热电联产进入了快速发展时期,如何进一步挖掘热电联产机组的节能潜力、降低发电成本显得尤为重要[1]。目前,我国仍存在较多母管制热电联产机组,相较于单元制机组,其锅炉与汽轮机之间的负荷分配关系更为复杂,如何进行合理的负荷分配优化,降低发电、供热成本及环境污染,成为亟待解决的问题。
热电厂在实际运行过程中大多采用3种传统方式进行热负荷调节:(1)热负荷平均分配;(2)由某一机组承担全部或基本热负荷,其他机组进行热负荷调节;(3)在保证热网供热指标的情况下由运行人员自主调节。但以上3种方式存在经济性不高、对人员运维经验依赖性强等缺点。
为解决这一问题,采用智能优化算法结合机理建模进行热电联产机组负荷分配优化方法成为热电负荷调节的主要手段。李蔚等[2]采用遗传-禁忌混合算法提高了负荷分配问题的求解速度。禹超[3]采用改进标准差分进化算法研究了热电机组的热力特性。顾慧等[4]利用禁忌粒子群算法分析了凝汽式、热电联产式和纯供热机组之间的组合对全厂可行域的影响。金洪吉[5]采用混沌粒子群算法进行负荷分配优化,并考虑了阀点效应对负荷分配的影响。廖金龙等[6]采用新型正弦余弦算法进行负荷分配优化,并引入一次调频约束,使优化后机组具有更高的一次调频能力与经济性。Yuan等[7]采用粒子群算法与人工鱼群算法的混合智能算法进行负荷优化分配,对2种不同种群进行测试,得出了该方法的适用范围。许可[8]采用蚁群算法,并利用Ebsilon对热力系统进行建模,验证了算法及模型的有效性。Jin等[9]采用带精英策略的快速非支配排序遗传算法(NSGA-Ⅱ),并考虑当地碳排放政策影响,进行多目标负荷优化分配。Shaheen等[10]采用蝠鲼觅食算法,结合可行域及阀点效应影响,进行了3次可行性测试,证明了该算法应用于热电联产能源系统的经济电力和热量调度问题的有效性。
然而,目前针对负荷优化分配的研究及新兴优化算法的应用主要集中在单元制机组,对于母管制热电联产机组的算法应用仍停留在二十世纪末兴起的粒子群算法、蚁群算法等。且不同于单元制机组,母管制机组锅炉与汽轮机数量通常并不匹配,主蒸汽由各个锅炉产出后统一汇入到一根母管,之后经由母管再分配到各汽轮机。因此,尽管母管制机组、单元制机组的负荷优化分配问题均属于低维度非线性优化问题,但母管制机组汽轮机与锅炉之间的负荷分配关系更复杂,负荷优化分配情况也更多样,在了解汽轮机、锅炉负荷特性以保证机理正确可行的基础上,需结合智能优化算法以提升求解效率,满足工程实际需要,降低系统整体能耗。黏菌优化算法(Slime Mould Algorithm,SMA)由 Li等[11]于2020年提出,其灵感来自于黏菌的扩散和觅食行为,属于元启发算法。该模型利用自适应权值模拟基于生物振子的黏菌传播波的正负反馈过程,形成具有良好探索能力的连接食物最优路径。自适应权值使SMA在保证快速收敛的同时保持一定的扰动率,避免捕捉局部最优解,并且在处理低维度问题时,表现出了良好的求解精度及鲁棒性,适用于母管制热电联产机组的负荷分配问题。SMA已被应用于光伏电池[12]、水电站运行[13]和风力发电[14]等领域。
因此,笔者以某“三炉两机”的母管制热电联产机组为研究对象,对汽轮机侧(以下简称汽机侧)、锅炉侧分别建立负荷优化分配的数学模型,首次将SMA引入机组负荷分配领域,按照先汽机侧、后锅炉侧的顺序,在满足供热需求的前提下分配汽轮机的抽汽量和排汽量,使汽耗率最低;并在此基础上,满足汽轮机总进汽量,对各锅炉主蒸汽量进行分配寻优,使全厂煤耗率最低。
1 母管制热电联产机组负荷特性
研究机组运行方式、获取正确的锅炉和汽轮机负荷特性是负荷优化分配的基础工作,也是确保负荷优化分配准确性的前提条件。
1.1 机组运行方式
某“三炉两机”母管制系统中,有3台循环流化床锅炉和2台 CB 30-13.24/3.5/0.981 型汽轮机。2台汽轮机为超高压单缸抽汽背压机,设计最大进汽量为 304.5 t/h,最大抽汽量为 80 t/h。抽背机组的电负荷完全取决于热负荷,属于“以热定电”机组,供热方式分为中压抽汽供热和低压排汽供热,运行方式如图1所示。
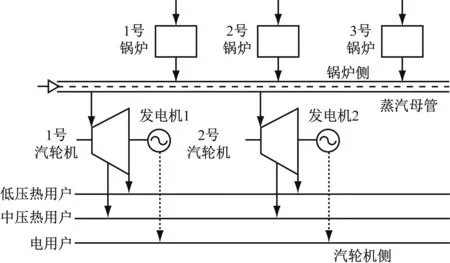
图1 运行方式示意图Fig.1 Schematic diagram of operation mode
1.2 锅炉负荷特性方程
3台循环流化床锅炉负荷特性通过现场试验获得。按照国家相关标准与试验规程,在1号锅炉、2号锅炉、3号锅炉布置测点,对各台锅炉的入炉煤煤质、排烟温度与成分、灰渣含碳量等参数进行测量。通过反平衡法对锅炉排烟热损失、气体未完全燃烧热损失、固体未完全燃烧热损失、散热损失以及灰渣物理热损失进行计算,得出3台锅炉在110~240 t/h 7种不同负荷下的锅炉效率,结果如表1所示。
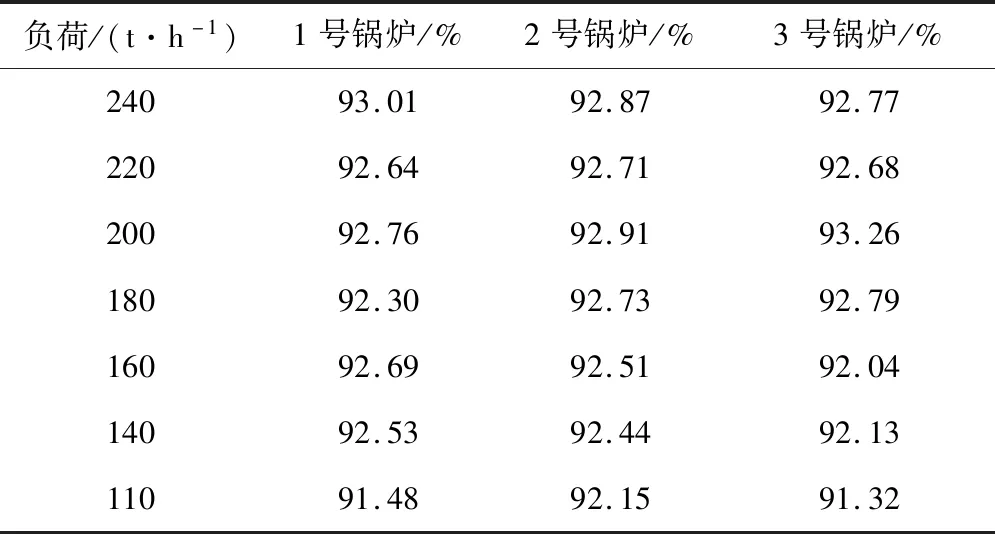
表1 不同负荷工况下各锅炉的锅炉效率Tab.1 Efficiency of the boiler under different load conditions
对3台锅炉的锅炉效率与产汽量特性方程进行多项式拟合,拟合方程为:
(1)
式中:ηi为锅炉效率,%;qm,bi为第i台锅炉产汽量,t/h;A0、A1、A2为多项式系数,如表2所示。
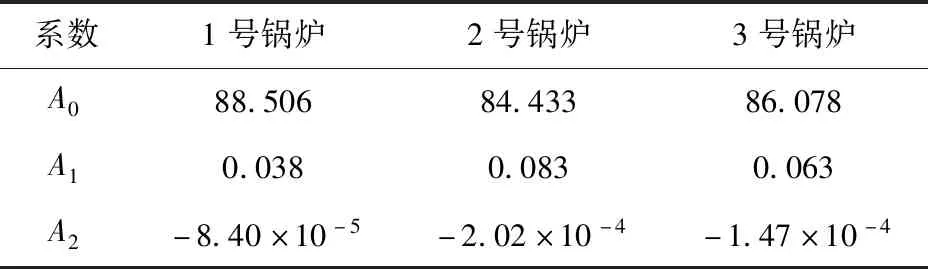
表2 特性方程多项式系数Tab.2 Polynomial coefficients of characteristic equation
由式(1)和表2得出的锅炉负荷特性方程如下:
(2)
式中:Bi为第i台锅炉煤耗量,kg/h;Hs,i、Hg,i分别为第i台锅炉主蒸汽焓值和给水焓值,kJ/kg;Q为煤的低位发热量,kJ/kg。
1.3 汽轮机负荷特性方程
汽轮机进汽量qm及发电功率P与中压供热抽汽量qm,g、低压排汽量qm,p之间存在函数关系。故当中压供热抽汽量和低压排汽量已知时,可根据对应函数关系确定汽轮机进汽量和发电功率。汽轮机进汽量特性方程f和汽轮机发电功率特性方程g分别为:
qm=f(qm,p,qm,g)
(3)
P=g(qm,p,qm,g)
(4)
为得到不同抽汽量、排汽量下汽轮机特性方程的具体参数,采用1号汽轮机、2号汽轮机的实际运行数据,分有中压抽汽、无中压抽汽2种情况对汽轮机的负荷特性方程进行拟合。以1号汽轮机为例,实际拟合汽轮机的负荷特性方程见表3。

表3 1号汽轮机负荷特性方程Tab.3 Load characteristic equations of No.1 steam turbine
2 负荷优化分配数学模型
母管制热电联产机组具有“以热定电”的特性,因此在进行负荷优化分配时,总体目标为在满足外界供热要求的前提下,通过对各汽轮机、锅炉间合理的负荷分配,实现全厂发电效率最大化,降低煤耗率,节约成本。针对母管制热电联产机组汽轮机、锅炉数量不匹配的特点,按照先汽机侧、后锅炉侧的顺序进行负荷分配。首先满足汽机侧的的供热需求,并可由此计算汽机侧总进汽量;再在满足汽机侧进汽量的前提下对锅炉侧进行分配,从而达到系统整体发电效率的最大化。
2.1 汽机侧负荷优化分配数学模型
汽机侧负荷优化分配的整体思路为:在满足总体中压供热量、低压供热量的前提下,通过改变不同汽轮机中压抽汽量和低压排汽量,按照式(3)和式(4)计算出对应汽轮机的进汽量和发电功率,再对比分析不同分配方式下的汽耗率,寻找最优的负荷分配方式。
2.1.1 汽机侧优化目标
目标函数为汽耗率最低:
(5)
式中:d为汽耗率,t/(MW·h);m为汽轮机数量;qm,i、qm,pi、qm,gi分别为第i台机组的进汽量、排汽量和抽汽量,t/h;Pi为第i台机组的发电功率,MW。
2.1.2 汽机侧约束条件
机组容量约束为:
qm,i,min≤qm,i≤qm,i,max
(6)
Pi,min≤Pi≤Pi,max
(7)
式中:qm,i,min、qm,i,max为第i台汽轮机允许最小和最大进汽量,t/h;Pi,min、Pi,max为第i台汽轮机最小和最大发电功率,MW。
抽汽量约束为:
qm,gi≤qm,gi,max
(8)
式中:qm,gi,max为第i台汽轮机允许最大中压供热抽汽量,t/h。
排汽量约束为:
qm,pi,min≤qm,pi≤qm,pi,max
(9)
式中:qm,pi,min、qm,pi,max为第i台汽轮机最小、最大排汽量,t/h。
供热负荷等式约束为:
(10)
(11)
2.2 锅炉侧负荷优化分配数学模型
锅炉侧负荷优化分配的思路为:在汽机侧优化得出最小汽耗率的分配方式下,计算得出汽机侧所需蒸汽量,即理论锅炉总产汽量;进而在满足锅炉总产汽量的前提下对各台锅炉产汽量进行分配,通过锅炉产汽量对应计算出各锅炉效率,结合给水焓值、主汽焓值以及煤的低位发热量可推算出各锅炉煤耗量,最后计算并比较整体煤耗率,得出最佳分配方式。
2.2.1 锅炉侧目标函数
目标函数为煤耗率最低:
(12)
式中:b为煤耗率;n为锅炉数量。
2.2.2 锅炉侧约束条件
容量约束为:
qm,bi,min≤qm,bi≤qm,bi,max
(13)
式中:qm,bi,min、qm,bi,max为第i台锅炉的最小和最大产汽量,t/h。
产汽量等式约束为:
(14)
式中:(qm,i)opt为第i台机组负荷优化分配后的进汽量,t/h。
3 黏菌优化算法
SMA中的黏菌主要依靠生物振荡器产生的传播波改变静脉内的细胞质流动,使其处于较好的食物浓缩位置。该模型利用自适应权值模拟基于生物振子的黏菌传播波的正负反馈过程,形成具有良好探索能力的连接食物最优路径。SMA具有收敛精度高、鲁棒性强的特点,且在低维度下尤为明显。
将黏菌的逼近食物行为模拟为数学方程,其位置更新方程如下:
X(t+1)=
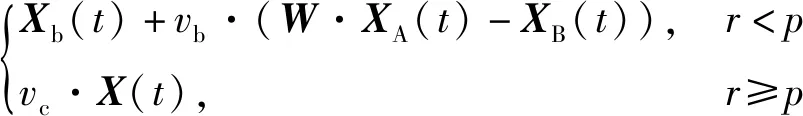
(15)
p=tanh|S(i)-FD|
(16)
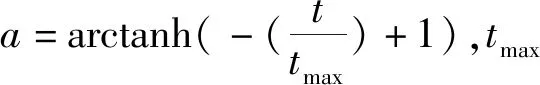
黏菌自适应权值W的表达式为:
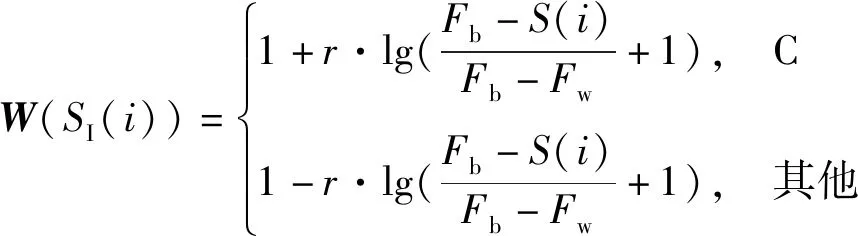
(17)
式(17)中参数r模拟了静脉收缩模式的不确定性。C表示S(i)中排名前一半的种群,模拟黏菌根据食物的权重调整其搜索模式。Fb表示在当前迭代过程获得的最佳适应度,Fw表示在当前迭代过程获得的最差适应度,SI(i)表示适应度序列(最小值问题中为递增序列)。
以汽机侧为例,应用SMA的具体步骤为:
(1)根据式(5)确定适应度。
优化变量为第i台汽轮机排汽量qm,pi和抽汽量qm,gi。
(2)模型与算法参数初始化,设置最大迭代次数。
(3)计算初始种群各个体适应度即汽耗率d的值。
(4)趋化循环。根据式(15)~式(17),进行个体位置更新,并保存种群中适应度最小的部分个体。
(5)判断是否达到迭代次数或满足迭代停止条件,若不满足转至步骤(3)。
(6)若满足条件,输出优化问题最优解,获得满足约束条件的使汽机侧汽耗率最低的抽汽量、排汽量。
对于锅炉侧算法,仅需基于步骤(1)~步骤(6)所得抽汽量和排汽量,得到所需总进汽量,并以煤耗率最低为目标函数,以各锅炉产汽量为优化变量即可获得最终优化结果。
4 算例分析
对母管制热电联产机组进行负荷优化分配,由于现场实际运行需要,中压供热量通常较小,汽机侧中压抽汽量由其中一台汽轮机抽出;主要通过改变低压供热量的分配,即2台汽轮机低压排汽量进行汽机侧的优化分配。
以某外界供热需求较高的典型工况为例,初始化设置最大迭代次数为500,根据外界供热需求量设置供热负荷等式约束,即排汽量为386.69 t/h,并由机组参数设置机组容量约束、排汽量约束等,优化前后的数据对比如表4所示。由表4可以看出,优化分配前后汽机侧中压供热抽汽量与低压排汽量总和不变,且机组整体汽耗率降低0.063 t/(MW·h),锅炉侧煤耗率降低0.126 kg/t,机组运行经济性得到提升。
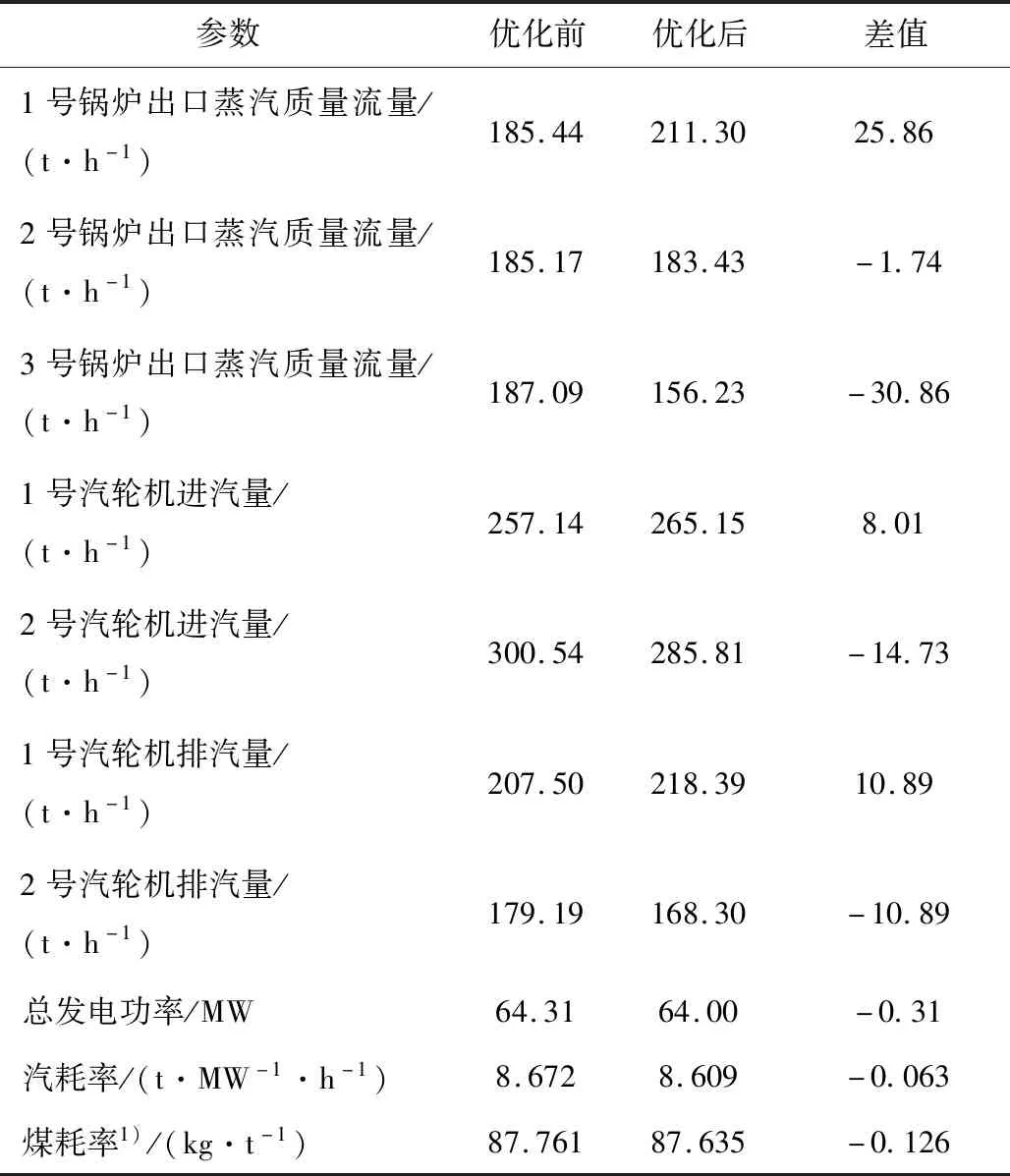
表4 SMA优化前后主要参数对比Tab.4 Comparison of main parameters before and after SMA optimization
为比较不同算法的求解精度,在相同工况下应用遗传算法(Genetic algorithm,GA)进行求解,优化前后结果见表5。
对比表4、表5可知,相同工况下,应用黏菌优化算法机组的整体汽耗率下降0.063 t/(MW·h),锅炉侧煤耗率降低0.126 kg/t;应用遗传算法机组的整体汽耗率降低0.054 t/(MW·h),锅炉侧煤耗率下降0.098 kg/t。因此,相较于遗传算法,应用黏菌优化算法求解负荷优化分配问题具有更好的求解精度。
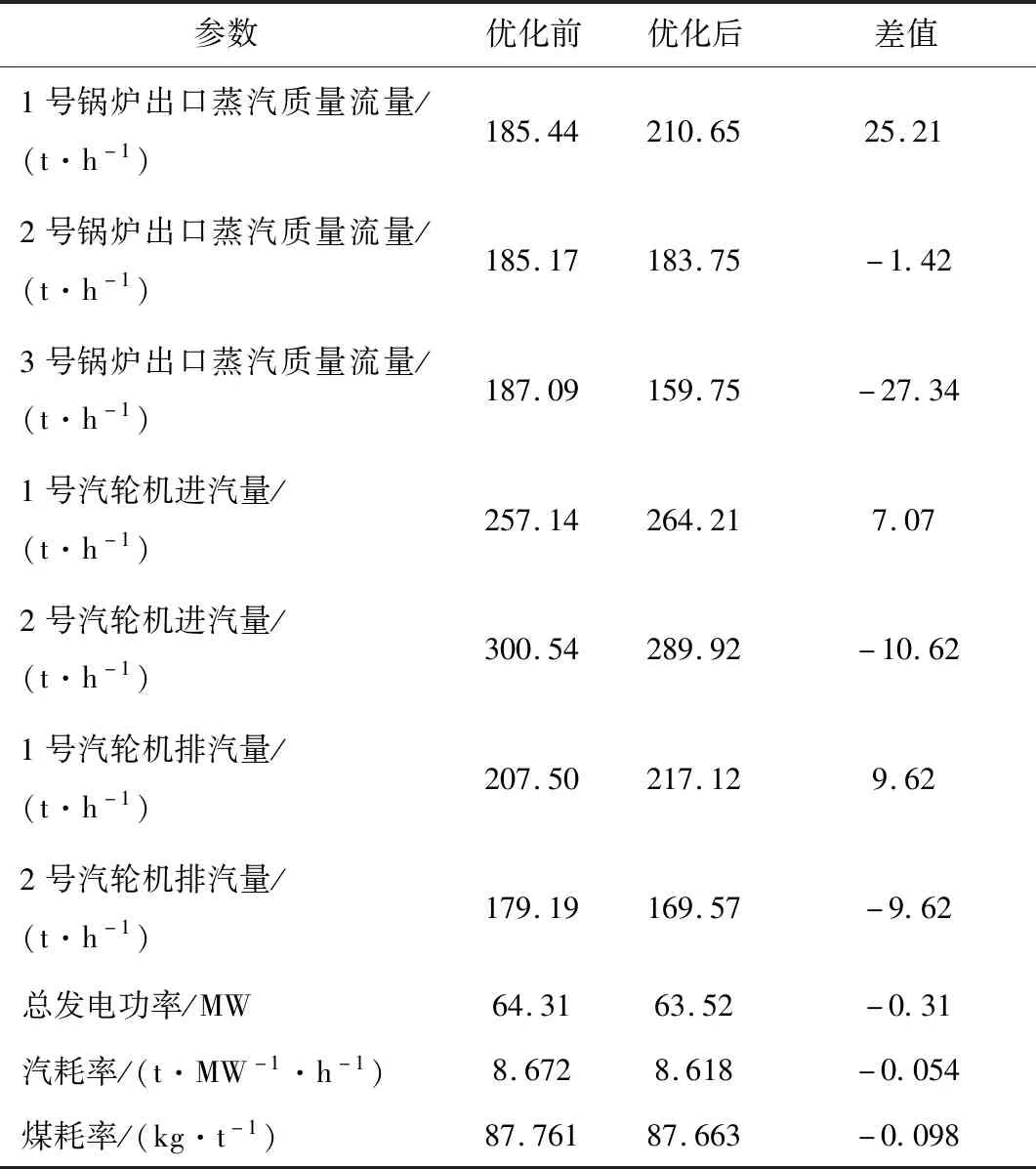
表5 GA优化前后主要参数对比Tab.5 Comparison of main parameters before and after GA optimization
为研究全工况下应用黏菌优化算法后的负荷优化分配效果,选取该电厂11月某全天现场数据进行分析。汽机侧排汽量变化如图2所示,表示了2台汽轮机承担的热负荷大小。结果表明在热负荷需求较低的00:00—08:00,可由2号汽轮机带全部热负荷;在热负荷需求较高时(09:00—17:00),应调整使1号汽轮机机承担更多热负荷,2号汽轮机相应降低热负荷;热负荷逐渐下降时(18:00—22:00)应调整使2号汽轮机承担更多热负荷,1号汽轮机相应降低热负荷,使汽耗率降低。
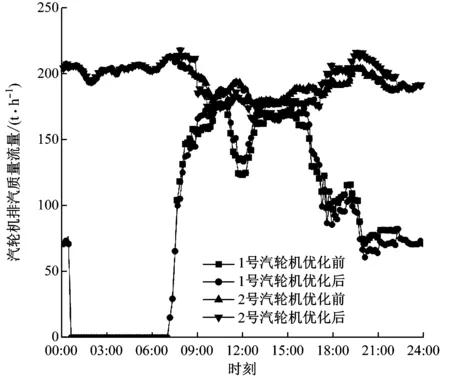
图2 排汽量变化曲线Fig.2 Variation of the exhaust flow
汽机侧优化分配后的汽耗率变化见图3。由图3可知,在各工况下,优化后的汽耗率均有不同程度降低,在热负荷较低的时间段(17:00—22:00),优化效果最好,最大汽耗率可降低0.289 t/(MW·h),节能效果可观。

图3 汽耗率变化曲线Fig.3 Variation of the steam consumption rate
对于锅炉侧,在满足汽机侧进汽量要求的前提下对不同锅炉产汽量进行分配,使煤耗率最低,优化结果见图4。由图4可知,锅炉侧负荷优化分配结束后,锅炉煤耗率在不同工况下均有不同程度的下降,且在低供热负荷工况下仍表现出较好的优化效果。
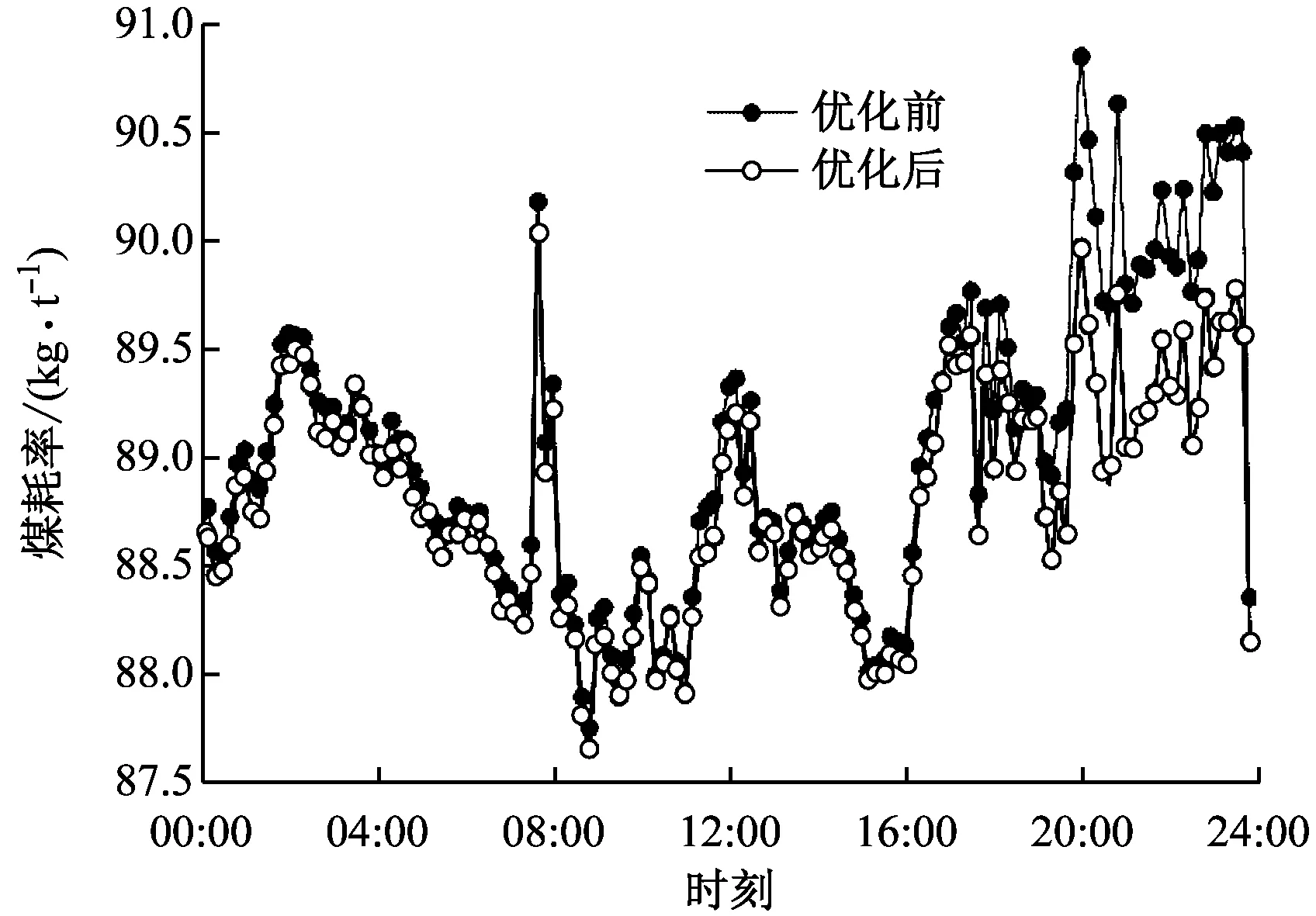
图4 锅炉煤耗率变化曲线Fig.4 Variation of the coal consumption rate
5 结 论
(1)基于锅炉、汽轮机负荷特性,针对母管制热电联产机组,提出了按先汽机侧、后锅炉侧的顺序分段进行负荷优化分配的方法,并引入最新的黏菌优化算法进行求解。
(2)对比黏菌优化算法与遗传算法的优化结果可以看出,将黏菌优化算法应用在负荷优化分配领域具有较好的求解精度。
(3)以某“三炉两机”的母管制热电联产机组为例,对比优化前后电厂实际运行结果发现,优化后的分配方案比优化前具有更低的汽耗率和煤耗率,且在较低供热负荷工况下仍表现出较好的优化效果,验证了模型的有效性。
