风力机变桨故障叶片双向强流固耦合研究
2022-04-18王渊博刘青松
王渊博,李 根,李 春,2,刘青松
(1.上海理工大学 能源与动力工程学院,上海 200093;2.上海市动力工程多相流与传热重点实验室,上海 200093)
风力机已实现大规模安装、运行和并网发电[1],但针对变桨故障[2]的气动及结构研究鲜见报道,故采用气动-结构耦合方法对风力机特定状态下的变桨故障叶片进行计算分析,以探究其在多物理场耦合作用下的气动特性及结构响应显得尤为重要。
对于风力机变桨故障,国内外学者进行了一些研究。Ronsten[3]基于相关实际测量数据,提出风力机停机后叶片状态将影响其力矩大小及压力分布。Chen等[4]通过研究台风“天兔”袭击汕尾红海湾风电场事件,指出变桨系统故障与风力机大面积严重损毁情况存在很大联系。Etemaddar等[5]经过对兆瓦级三叶片水平轴风力机桨距角传感器误差产生的影响进行分析,发现误差越大风力机主轴轴承振动越明显。任年鑫等[6]研究了台风环境下水平轴风力机顺桨停机后变桨故障与变桨成功叶片的受载情况,模拟结果表明变桨故障叶片载荷总是大于变桨成功叶片。从上述研究可知,变桨故障对风力机叶片受载影响极大,故此时叶片结构也最危险,然而目前关于结构侧应变或应力分布的研究还较少。此外,风力机切出风速下停机后变桨故障叶片入流风速及受载均较大,但该风况下的变桨故障研究却鲜见报道。
虽然针对风力机变桨故障气动与结构的研究较少,但在风力机其他方面气动-结构耦合的研究成果相对较多。Behrouzifar等[7]提出结合风力机致动盘模型与有限元分析梁单元进行兆瓦级风力机气动-结构耦合数值模拟,将计算结果与已有研究数据进行对比后得出,该方法能较准确地模拟风力机气动特性及结构动力学响应。但此方法不能计算风力机周围流动状况,因此无法对影响固体域结构响应的流体域因素进行更深层次的分析。王渊博等[8]耦合开源计算流体力学软件OpenFOAM与风力机气弹软件FAST对串列布置的2台NREL 5 MW风力机的风场进行数值计算,发现下游风力机受上游风力机尾迹影响严重,输出功率及结构动力学响应与上游风力机均不相同。然而,该研究中固体域采用多体动力学模型[9]结合模态叠加法[10]进行叶片结构动力学响应求解,无法获得叶片详细应变情况及内部应力分布。
综上,笔者基于计算流体力学及有限元法相结合的双向强流固耦合方法,研究NREL 5 MW风力机在切出风速下停机后的变桨故障叶片流体域和固体域状态,以期为叶片结构设计及风力机运行提供更全面的参考数据。
1 流固耦合及研究对象
1.1 双向强流固耦合
流固耦合既涉及流体流动求解,还需对固体结构进行计算,同时还要保证流体域与固体域之间数据交换的正常推进,并考虑交换频率及两侧数据插值等[11]。此外,还需根据所分析问题及研究目的选择强流固耦合或弱流固耦合,这主要基于流体域与固体域间物理变量场耦合程度(受结构侧响应速率影响)的差异进行区分,其中强流固耦合的流体域与固体域变量需在非常小的时间步长内保持一致。所研究切出风速下变桨故障叶片的气动侧和结构侧变量场耦合程度极高,故采用双向强流固耦合,其流程如图1所示。

图1 双向强流固耦合流程图Fig.1 Flow chart of two-way strong fluid-structure coupling
双向强流固耦合运算时固体域结构变形数据需传递给流体域计算对象,以使流体域空间形状作出相应改变,因而流体域网格亦需重新布局。流固耦合流体域网格再次调整方法较多,如网格重构、网格变形及重叠网格技术等,笔者基于计算流体力学软件STAR-CCM+的Morphing功能实现网格变形。在流固耦合数值运算过程中,Morphing功能在流体域内布置若干控制点以控制流体域网格顶点移动,故可使流体域计算对象与固体域结构变形始终保持匹配,同时还能保证流体域网格具有较高质量。
图2为Morphing功能的控制点(位置固定不变的圆点)及网格变形示意图。

(a)变形前
1.2 叶片参数化建模及复合材料
叶片是风力机最关键的部件[12],对其基于参数化技术进行建模是风力机整机实体模型构建过程中难度最大的环节。利用Unigraphics NX软件建立NREL 5 MW风力机叶片三维实体模型,共分为以下3个步骤:(1)准备叶片各形状控制截面对应翼型的二维归一化坐标及其弦长和扭角数据;(2)根据形状控制截面上翼型的弦长和扭角,对归一化后翼型二维坐标(x,y)点集进行相应缩放及旋转变换;(3)将全部翼型数据导入Unigraphics NX软件,并通过一系列相关操作最终实现叶片成型。步骤(2)中利用式(1)进行翼型的缩放及旋转变换:
(1)
式中:x、y分别为翼型归一化后的横、纵坐标;xAero为翼型气动中心;c和β分别为弦长和扭角;x′和y′分别为缩放及扭转变换后翼型的横、纵坐标。
最终NREL 5 MW风力机叶片三维实体模型及局部关键部位放大图如图3所示。

图3 NREL 5 MW风力机叶片模型Fig.3 Blade model of the NREL 5 MW wind turbine
完成NREL 5 MW风力机三维实体建模后,双向强流固耦合气动侧数值模拟可直接基于该模型进行流动计算。但结构侧相对较复杂,因为对固体结构进行有限元分析还需三维模型具备相关材料属性。对于风力机而言,塔架、机舱和轮毂等部件材料较为单一,无论工业制造还是数值分析在材料设置方面相对叶片均较简单,而叶片需通过极其复杂的铺层技术设计复合材料以保证结构性能[13]。为满足该风力机叶片结构力学性能要求,共选取9种单一材料,每种材料性能皆不相同。通过对单一材料种类、纤维方向以及铺层顺序进行组合便可得到适用于风力机叶片各部位的复合材料。如叶片主梁帽需要承担弯曲载荷,故可选择抗拉性强的碳纤维和玻璃纤维,并使纤维方向顺着叶片展向进行铺层,其他部位铺层方法类似。分析叶片所有部位对复合材料性能的要求并结合各单一材料属性统一规划之后,最终铺层方案如图4所示。该方案与真实风力机叶片结构设计、制造工艺相同[14],从而保证计算结果能够直接为相关设计制造及实际工程问题提供参考。
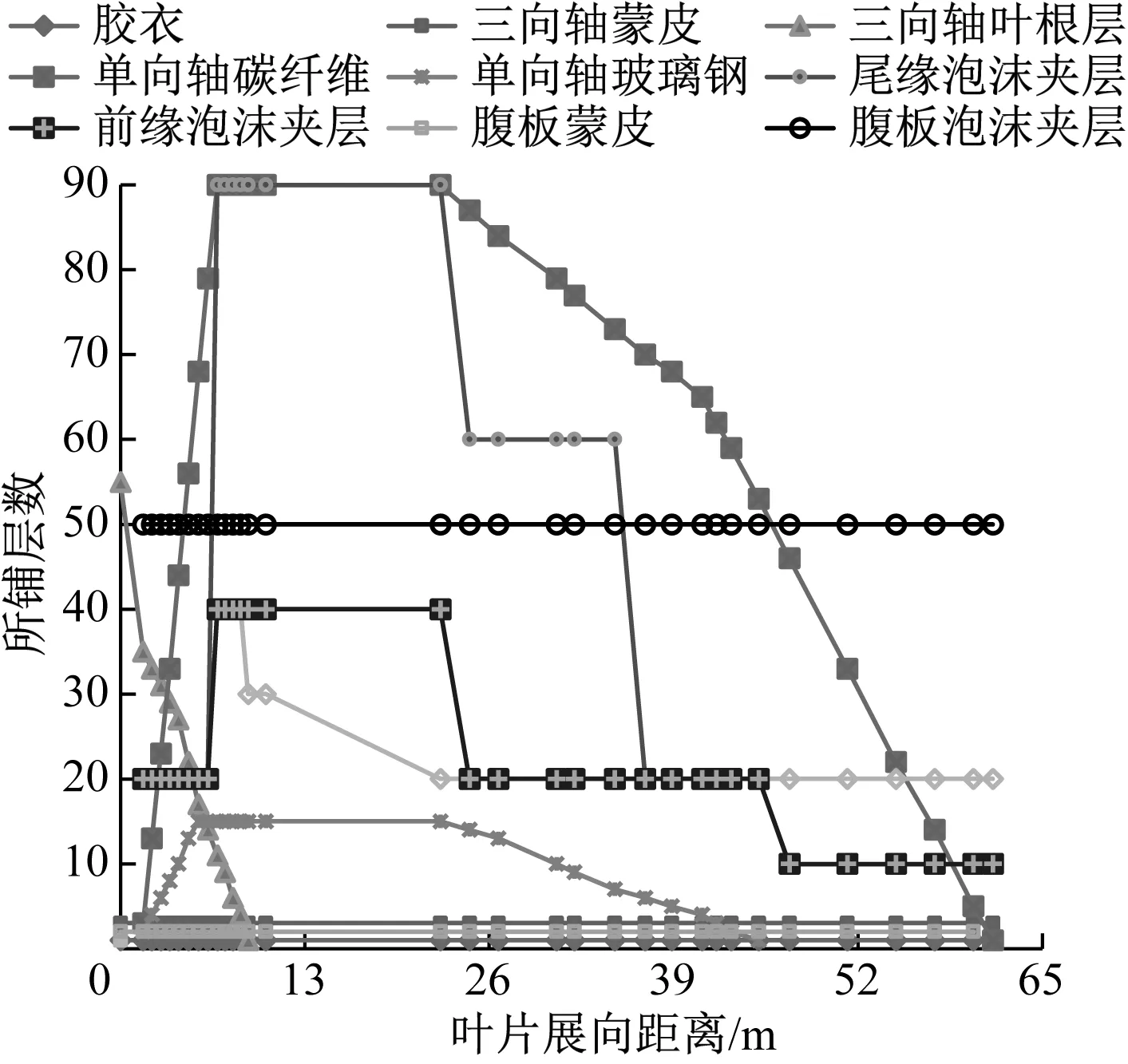
图4 叶片铺层方案Fig.4 Blade laying scheme
2 数值计算
2.1 气动侧模型
变桨故障叶片气动载荷及流场特性与变桨成功叶片不同,这也是引起结构响应变化的根本原因。因此,首先需要对变桨成功叶片和变桨故障叶片的气动载荷及流场特性进行分析,以探究引发结构侧状态产生变化的气动侧因素。同时通过对比全叶轮模型(Full Rotor Model,FRM)和单叶片模型(Single Blade Model,SBM)的数值计算结果,为减少双向强流固耦合计算量方面提供理论依据。
NREL 5 MW风力机轮毂高度为90 m,叶轮直径达126 m,属大型水平轴风力机,故风剪切对其影响不可忽略。目前,风剪切模型主要有对数率和指数率2种[15],此处选用指数率进行计算:
vH=v0×(H/H0)λ
(2)
式中:H0为参考高度,此处取轮毂高度90 m;H为海拔高度;vH为海拔高度H处的风速;v0为参考高度H0处的风速;λ为地面粗糙度指数。
风力机气动载荷分析需通过局部坐标系(整个计算域坐标系为全局坐标系)定义各叶片不同方向力矩。本文叶片坐标系位于叶根,其中Z轴从叶根指向叶尖,X轴由叶片前缘指向后缘,Y轴根据右手定则与Z轴以及X轴所定义平面垂直。需指出的是,风力机进行变桨时叶片坐标系也绕变桨轴与叶片同步旋转,因此可基于该局部坐标系定义叶片各方向力矩。将叶片力矩分解为基于X轴的挥舞力矩和基于Y轴的摆振力矩,图5为叶片坐标系及各方向力矩示意图。

图5 叶片坐标系及各方向力矩Fig.5 Blade coordinate system and torque in all directions
为降低计算域边界对数值模拟的影响,并减小风洞阻塞效应[16-17],需尽可能扩大计算域尺寸以增加风力机叶片与各边界间的距离。本文计算域如图6所示,其中右下角坐标系为数值模拟全局坐标系。以D(126 m)表示风力机叶轮直径,计算域在X方向尺寸为8.0D,Y方向尺寸为6.0D,Z方向尺寸为3.5D,风力机在X方向距入口以及在Y方向距两侧面均为3.0D。入口边界条件为指数率风剪切速度入口,参考高度处风速大小是风力机切出风速25 m/s,地面粗糙度指数选为0.16[18];出口为压力出口,参考压力值为101 325.0 Pa(一个标准大气压);地面为无滑移壁面,顶面是对称平面,两侧面采用周期性边界条件,即计算域一侧面网格节点与另一侧面网格节点一一对应,某侧周期边界计算域外“镜像单元”信息由紧邻另一侧周期边界计算域内的单元提供。

图6 计算域以及边界条件和风力机位置Fig.6 Calculation domain,boundary conditions and wind turbine location
计算域最终网格分布如图7所示,可以看出其全部采用多面体网格类型。

(a)叶片表面网格
需要说明的是,与四面体网格相比,多面体网格能以更少数量达到相同计算精度。多面体网格最大的优点为有较多相邻控制体,故能更精确地计算网格中心点间的梯度,当其被拉伸时亦不像四面体网格那样非常敏感,甚至在计算域边角处可正常计算梯度及局部流动,因此更适合基于计算流体力学和有限元法的双向强流固耦合数值模拟时实现网格变形。STAR-CCM+计算流体力学求解器采用有限体积法,故能基于多面体网格进行计算。利用STAR-CCM+前处理创建高质量多面体网格,且由于达到切出风速时叶片多处于失速分离状态,因此壁面边界层需采用低y+处理方式(y+<1)。近壁面网格高度为5×10-4m,边界层网格共24层,总厚度0.1 m。同时为使风力机数值模拟准确度更高,需对其尾迹区域加密。
数值计算采用隐式非定常算法,时间步长为0.001 s,对流项与时间项的离散均使用二阶格式,压力-速度解耦基于Simple算法,湍流处理采用SSTk-ω模型,湍流强度取0.05,湍流长度尺度为1.0 m。根据叶片坐标系在计算过程中监测并存储叶片各方向力矩,当数值模拟运行至载荷处于相对稳定或呈周期性振荡时则判定为已收敛。
2.2 结构侧模型
图8为流固耦合结构侧计算模型。

图8 流固耦合结构侧计算模型Fig.8 Structure calculation model of the fluid-structure coupling
风力机叶片几何模型由片体(无厚度曲面)构建,这是由于有限元分析中若三维结构某一方向尺寸远小于另外2个方向尺寸即可采用片体模型[19],既能保证精度又可节省计算资源。同样为节省计算资源,将风力机叶片划分为结构化网格。有限元分析中片体结构化网格适合使用S4R单元,这是一种通用壳单元类型,既可应用于厚壳问题求解,也能应用于薄壳模型计算。S4R单元为基于减缩积分的四节点单元,采用减缩积分是因为完全积分在求解承受弯曲载荷的结构时易产生剪切闭锁现象,将会导致单元过硬,此时即使划分非常精细的网格,其计算精度仍很差,而减缩积分相较于完全积分在每个方向上少使用一个积分点,可消除剪切闭锁现象,且能保证较高的计算精度[20]。此外,风力机叶片根部采用Abaqus中的运动耦合约束,未采用分布耦合约束是由于其为一种较柔软的约束,而真实风力机叶根通过一圈螺栓固定在轮毂圆形接口上,并不会发生明显变形,因而刚度较大的运动耦合约束与实际情况更为吻合。将叶根一圈通过运动耦合约束在叶根圆形的中心点(即约束点)上,然后为该约束点施加ENCASTRE边界条件[21],可对6个自由度同时全部进行约束。不对叶根直接使用ENCASTRE边界条件是因其会作用于叶根最外边一圈S4R单元节点的自由度,最终会影响数值模拟结果的准确性。
3 结果与分析
3.1 无流固耦合气动模拟结果
载荷过大会造成风力机结构破坏,其周期性变化引发的振动也会导致疲劳失效。故需从时间维度分析风力机气动载荷时域脉动特征。图9为SBM和FRM的挥舞力矩、摆振力矩时域图。对比图9(a)和图9(b)可知,SBM与FRM的挥舞力矩和摆振力矩时域曲线基本重合,初步证明基于SBM计算的可行性。
为研究载荷脉动频率特征,对力矩脉动时域数据进行频域分析,进一步对比SBM与FRM载荷脉动值的差异。将SBM和FRM的挥舞力矩和摆振力矩脉动时域序列进行快速傅里叶变换(Fast Fou-rier Transform,FFT),得到表1中的载荷脉动主要刺激频率。由表1可以看出,SBM与FRM的挥舞力矩和摆振力矩的主要刺激频率相同或极其接近,这也进一步证明水平轴风力机SBM与FRM载荷脉动的差异非常小,使用SBM代替FRM进行数值计算具有较高的准确性及可行性。

(a)挥舞力矩

表1 SBM和FRM的载荷脉动主要刺激频率Tab.1 Main stimulation frequencies of load pulsation in SBM and FRM Hz
流场参数是外在物理现象的内在原因,为更深层次地比较SBM与FRM的数值模拟结果,截取经过叶片顶点且与Z轴垂直的平面,对比该截面上SBM与FRM在Z轴方向的叶尖涡量场,如图10所示。可以观察到SBM与FRM的叶尖涡大小及位置几乎完全相同,说明SBM与FRM的流场流动状况极为接近,这也是SBM与FRM载荷脉动主要刺激频率和力矩时域曲线差别甚微的根本原因。
3.2 双向强流固耦合分析
基于SBM模型对切出风速下顺桨停机后的变桨故障叶片进行双向强流固耦合数值模拟。其中流固耦合模拟流体域气动载荷利用STAR-CCM+求解,固体域结构响应采用Abaqus计算,气动侧与结构侧数据交换基于Co-Simulation程序进行。此外,为保证计算过程稳定且收敛,双向强流固耦合时间步长比3.1节的气动计算小一个数量级,为5×10-4s。这是因为若时间步太长,则每个时间步内风力机叶片变形比较大,此时结构侧与气动侧进行数据交换时很可能因位置不匹配而失败,最终将导致计算中断[22]。

(a)SBM
图11为双向强流固耦合变桨故障叶片与变桨成功叶片气动力矩时域图。从图11可以看出,双向强流固耦合计算的挥舞力矩波动范围比图9无流固耦合挥舞力矩波动范围更大,这是因为流固耦合作用下叶片结构会发生变形,导致组成叶片叶素的入流角、攻角及相对速度等均发生改变,最终造成叶片升阻力处于动态变化中而产生较大波动。双向强流固耦合各方向力矩的平均值与气动模拟基本相同,仅波动范围差别较大,说明本文计算结果准确性与可信度均较高。对比双向强流固耦合变桨成功与变桨故障叶片的气动力矩,能够发现在切出风速下变桨故障叶片挥舞力矩比变桨成功叶片整体大一个数量级,变桨故障叶片最大挥舞力矩为变桨成功叶片最大挥舞力矩的13.8倍。因此,若风力机出现变桨故障,其在切出风速下受到的载荷较大,如果风速继续增大,风力机叶片结构将会有发生断裂失效的风险。
图12为流场中过叶片展向中点且与Z轴垂直截面的速度云图。对比图12(a)和图12(b)可以看出,变桨故障叶片发生了显著变形,而变桨成功叶片变形并不明显,这与图11中力矩大小吻合较好。切出风速下变桨故障叶片桨距角仍为风力机额定风速时的桨距角(0°),此时来流不仅风速较大,且与叶片压力面几乎垂直,因此可产生相当大的气动载荷。同时叶片因为柔性发生变形,导致气动力大小频繁改变。而对变桨成功叶片,来流从叶片前缘吹向叶素尾缘,虽然切出风速较大,但此时攻角几乎为0°,故所产生的气动力非常小,不足以使叶片发生明显变形且气动力较为稳定。此外,还可以发现变桨故障叶片后方的尾迹比变桨成功叶片更为明显,范围更大且速度更小,说明变桨故障叶片从来流中吸收了更多能量,因此比变桨成功叶片所受载荷更大。

(a)挥舞力矩

(a)变桨故障
图13为双向强流固耦合数值模拟过程中基于叶片坐标系监测的叶尖挥舞方向(Y轴)和摆振方向(X轴)位移。由图13可知,变桨故障叶片挥舞方向的位移比变桨成功叶片挥舞方向位移大一个数量级,变桨故障叶片最大叶尖位移为变桨成功叶片的14.1倍。这与图12流场速度云图和图11气动力矩变化相吻合,证明了本文计算结果的准确性及可信度。

(a)变桨故障
从图13还可以看出,无论变桨故障叶片还是变桨成功叶片,挥舞方向叶尖位移均为叶片Y轴负方向。这是因为对于变桨故障叶片,叶片坐标系Y轴负方向为来流方向,此时来流几乎垂直吹向变桨故障叶片的压力面,因此变桨故障叶片挥舞方向为Y轴负方向。对于变桨成功叶片,来流从叶片前缘吹向叶片尾缘,因此叶片挥舞方向位移为叶片吸力面方向,即叶片坐标系Y轴负方向。
双向强流固耦合可基于有限元分析计算出叶片的应力及应变,图14为切出风速下变桨故障叶片和变桨成功叶片在数值模拟过程中0.9 s时的Mises应力示意图,选取0.9 s是由于图13中显示该时刻叶尖位移最大。从图14可以看出,变桨故障叶片应力比变桨成功叶片的应力大一个数量级,这与前文分析的气动力矩和叶尖位移结果完全匹配。从图14可以看出,与变桨成功叶片相比,变桨故障叶片应力集中分布范围更广。且放大图显示,变桨故障叶片出现了轻微压缩屈曲不稳定现象,这是因为叶尖位移在0.9 s时最大,叶片应变此时也最明显。但紧接着叶尖位移减小,压缩屈曲迅速消失,因此该瞬态失稳并未造成叶片结构破坏。相对于应力超限造成的结构强度破坏,屈曲不稳定对风力机结构的危害更大[23]。因为上述这种瞬态失稳现象一旦出现其他因素影响,很可能不会消失反而变得更为严重,从而导致屈曲不可逆,最终造成叶片断裂。而变桨成功叶片并未发生压缩屈曲不稳定现象,这是因为相较变桨故障叶片,变桨成功叶片的叶尖位移小一个数量级,叶片变形较弱,不足以使叶片出现瞬态失稳,这也证明风力机在达到切出风速时顺桨操作对于风力机结构保护非常有效。此外,变桨故障叶片在叶根圆柱向翼型过渡区也产生了比其他区域更明显的应力集中现象,虽然在目前风况下未表现出屈曲失稳,但若环境因素发生变化则应变很可能继续增大,故该位置的应力集中应引起足够重视。

图14 双向强流固耦合叶片Mises应力Fig.14 Mises stress of blade under two-way strong fluid-structure coupling
4 结 论
(1)SBM与FRM的力矩时频域数据、主要刺激频率以及涡量场强度和分布差别均较小,故采用能节省大量计算资源的模型SBM进行双向强流固耦合数值计算是可行的。
(2)变桨故障叶片比变桨成功叶片的受载及叶尖位移更大。且结构侧有限元分析结果显示,变桨故障叶片应力、应变集中现象比变桨成功叶片更为严重,且出现了瞬态屈曲失稳现象。
(3)叶片在双向强流固耦合方法下的挥舞力矩波动范围比无流固耦合时明显更大,但两者平均值大小基本相同。
