中国海域及邻区自适应空间平滑地震活动模型

吴 果 冉洪流 周 庆 谢卓娟

1)中国地震局地质研究所， 活动构造与火山重点实验室， 北京 100029 2)应急管理部国家自然灾害防治研究院， 北京 100085

0 引言

中国领海幅员辽阔， 沿海地区是中国的经济重心。随着近年来“21世纪海上丝绸之路”战略构想的提出， 滨海及海域的工程建设和资源开发日益增多。然而， 中国海域及邻区受到欧亚板块、 印度-澳大利亚板块、 菲律宾海板块和西太平洋板块的相互作用(图 1)， 构造背景复杂， 地震频发(刘光鼎， 1992； 臧绍先等， 1996； 彭艳菊等， 2008)。海域地震严重影响沿海地区的经济建设和社会稳定， 也威胁到海洋资源开发的安全(丁海平等， 2011； 谢卓娟等， 2020)。因此， 分析中国海域及邻区的地震活动特征， 建立相应的地震活动模型成为日益迫切的需求， 也是中国下一代地震区划图的工作重点之一(李小军等， 2020)。

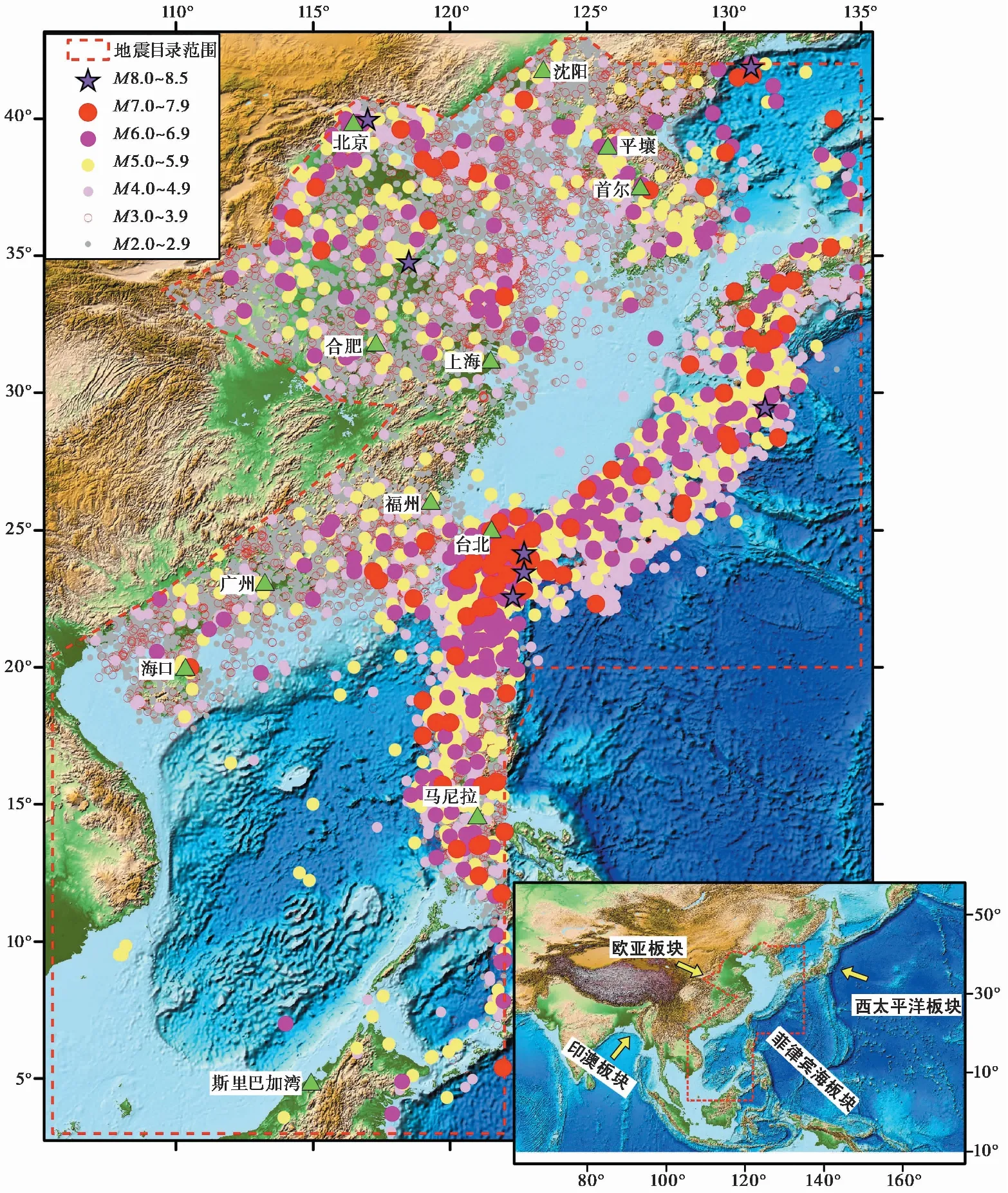
图 1 中国海域及邻区震中分布图(1767BC—2018年10月)Fig. 1 The distribution map of earthquakes in China seas and adjacent areas(1767BC—2018-10).高程数据引自文献(1)https： ∥www.ngdc.noaa.gov/mgg/global/。

地震目录是地震活动分析的重要基础资料之一。与大陆地区不同， 海域的地震监测台网密度有限、 地震资料积累不足(林趾祥等， 1999)。长期以来中国的地震目录编录工作都集中于中国大陆及外延的近海地区(李善邦， 1960； 中央地震工作小组办公室， 1971； 顾功叙， 1983a， b； 国家地震局震害防御司， 1995； 中国地震局震害防御司， 1999； Chengetal.， 2017)。这些成果在中国的抗震设防、 地震预测预报等工作中发挥了重要作用， 但是对于远海、 俯冲带及周边邻近海域鲜有涉及， 只有吴戈等(2001)对黄海及其沿岸的历史地震目录进行了编目和研究。依托于国家重点研发计划项目“海域地震区划关键技术研究”， 谢卓娟等(2020)通过广泛收集全球地震台网的地震资料， 首次编录了中国海域及邻区统一震级标度为MS的地震目录(图 1)。该目录为进一步分析中国海域及邻区的地震活动特征提供了基础。

空间平滑模型(Smoothed Seismicity Model， SSM)是目前国际上应用最为广泛的基于地震目录的地震活动模型之一， 该模型通过空间平滑函数/核函数(Kernel function)将记录到的中小地震发生率向震中附近平滑分配以预测未来的发震概率分布(Kafkaetal.， 2000)。SSM自Frankel(1995)提出至今， 已经在国际上得到广泛应用， 并成为美国国家地震区划图的一种基础模型(Frankeletal.， 2000； Petersenetal.， 2008， 2015； Fieldetal.， 2014； Khodaverdianetal.， 2016； Akincietal.， 2018； Assatouriansetal.， 2019)。由于传统的SSM对同一震级档的地震的平滑半径取相同值， 因此又被称为固定平滑半径的SSM(Petersenetal.， 2015)。

Helmstetter等(2007)提出了自适应空间平滑地震活动模型(Adaptively Smoothed Seismicity Model， ASSM)， 对传统的SSM做了改进： 1)根据预测效果自动确定每个输入地震的平滑半径； 2)自动调节平滑半径适应地震的空间分布密度。ASSM模型连续2次在“地震可预测性合作研究”计划(Co1laboratory for the Study of Earthquake Predictability， CSEP)的5a期中长期地震预测竞赛中取得最佳成绩(Zecharetal.， 2013； Straderetal.， 2017； Schorlemmeretal.， 2018)。因此， ASSM迅速地被广泛应用于全球的地震预测和地震危险性分析中(Kaganetal.， 2010； Werneretal.， 2010， 2011； Zecharetal.， 2010； Wangetal.， 2011； Helmstetteretal.， 2014； Moschetti， 2015； Talebietal.， 2017； Karaca， 2018)， 并于2014年被正式引入美国国家地震区划图(Petersenetal.， 2015， 2020)和美国加州地震概率工作组(Working Group on California Earthquake Probabilities， WGCEP)的UCERF3模型中(Fieldetal.， 2014)。

国内和国际一些学者和机构已经多次将SSM用于中国研究区。Rong等(2002)将SSM用于评估中国大陆的潜在发震能力； 多位学者以中国北部或者中国大陆为研究区， 用SSM建立地震活动模型并以此为基础开展地震危险性分析(Yangetal.， 2008； Xu， 2019； Fengetal.， 2020)； 中国第5代全国地震区划图中将SSM引入并作为确定潜源空间分布函数的因子之一(潘华等， 2013)； 最近的研究用SSM来描述中小地震的发震概率分布， 以配合断层模型建立川滇地区或中国大陆的地震活动模型(程佳等， 2020； Rongetal.， 2020)。

国内学者对于ASSM的研究较少， 只有Wu等(2019)将其用于建立青藏高原东部地区的中长期地震预测模型。在该工作中， Wu等(2019)针对中国历史地震记录时间长、 地震记录水平随时空变化的特点， 改进了Helmstetter等(2007)的算法， 使其可以充分利用完整性随时间和空间同时变化的地震记录， 同时采用空间扫描的方法求取b值， 以更好地体现地应力的分布(吴果等， 2019； 王少坡等， 2020)， 从而实现预测效果的优化。

通过上述分析可知， 由于此前缺乏海域统一的地震目录， 前人对于SSM的研究都是以中国大陆及邻近地区为研究区， 尚未以整个中国海域及邻区作为研究对象。只有张力方等(2013)在福州—天津沿线近海地区做过相关研究， 而其他海域的相关工作尚属空白。此外， Helmstetter等(2007)提出的ASSM在地震中长期预测中表现优异， 但国内相关研究很少， 尚未将其应用于中国广大的海域地区。

本文基于谢卓娟等(2020)编录的中国海域及邻区的统一震级标度的地震目录， 采用分震级档累积地震数-时间曲线分析各个地震带的地震目录完整性， 进一步采用极大似然法拟合地震活动参数。在此基础上， 采用Wu等(2019)改进后的自适应空间平滑算法， 充分利用完整记录水平随时间和空间变化的地震数据， 建立中国海域及邻区M≥5.0地震年发生率的分布模型， 并采用概率增益函数对不同参数设置下的模型表现予以评价。最后分析了模型的优点和局限性， 并给出使用建议。

1 地震目录和完整性分析

1.1 地震目录来源和前处理

本文的地震数据来自谢卓娟等(2020)新编录的中国海域及邻区的地震目录， 该目录汇集了中国大陆、 中国台湾、 日本、 韩国、 菲律宾等国家和地区的地震数据， 时间跨度从公元前1767年—2018年10月， 是截至目前数据收集最为完整的中国海域及邻区地震目录， 共包含M2.0以上地震事件61285条。为了满足后续用于编制海域地震区划图的需要， 该目录的统计范围除了渤海、 黄海、 东海和南海等主要海域外， 还向邻区有所延伸， 乃至包括中国大陆沿海的地震区带(图 1 中红色虚线框)。此外， 考虑到面波震级MS是国内工程地震界通用的震级标度， 为了与前人的工作保持延续性， 谢卓娟等(2020)采用正交回归法拟合了不同震级标度之间的转换关系， 将地震目录的震级标度统一为面波震级MS(Xieetal.， 2021)。

类似前人在地震预测和地震危险性分析时的工作(Helmstetteretal.， 2007； Wangetal.， 2011； Petersenetal.， 2015； Talebietal.， 2017； 程佳等， 2020)， 本文采用国际上广泛应用的Gardner等(1974)提出的算法删除前、 余震(Wiemer， 2001)。共发现地震丛集6353个， 包括31835个地震事件。除丛后的地震目录包含29450条地震记录， 其中M5.0以上主震分布见图2a。

1.2 完整性分析

采用记录时间长但不完整的地震目录会给地震活动参数的评估带来偏差， 无益于提高地震活动模型的质量(徐伟进等， 2014； Talebietal.， 2017)， 故在建立模型之前需要分析地震目录的完整性。区别于Wu等(2019)的做法， 本研究并没有采用空间扫描的方法求取每个网格点的地震目录完整性， 这是基于2方面考虑： 1)海域的地震监测台网密度有限， 有地震完整记录的时间较短(林趾祥等， 1999)； 2)如图 1 所示， 研究区内的地震分布极不均匀， 在东海、 南海等大片海域地震记录十分稀少。以上原因导致若采用空间扫描法， 很容易遇到地震记录达不到数据分析所需的样本量下限的情形。

因此， 本研究延续中国第5代全国地震区划图的做法(潘华等， 2013)， 即以地震区带为统计单元进行完整性分析。“海域地震区划关键技术研究”项目组依据新编制的海域活动构造框架图中主要构造单元的边界对第5代区划图的地震区带划分方案做了部分调整， 使得地震区带的边界基本与二、 三级构造单元的边界重合(高战武等， 2021)。主要调整了东海地震带、 台湾东部地震带和南海地震区的边界， 其中对台湾东部地震带进行了调整并扩充了范围， 改称台湾南-马尼拉海沟地震带。同时， 沿琉球海沟划分出琉球海沟地震带。调整后的地震带分布见图2b。

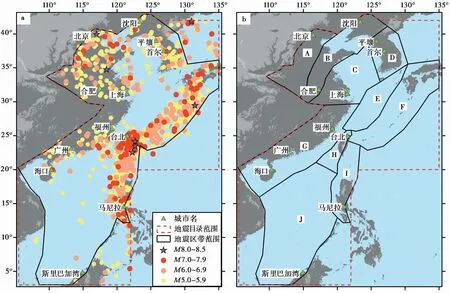
图 2 a 中国海域及邻区M5.0以上主震的震中分布图； b 研究区内的地震带分布图(引自高战武等， 2021)Fig. 2 The distribution map of M≥5.0 main shocks in China seas and adjacent areas(a)； the locations of seismic zones in the study area(b)(Cited from GAO Zhan-wu et al.， 2020).A 华北平原地震带； B 郯庐地震带； C 长江下游-南黄海地震带； D 朝鲜地震带； E 东海地震带； F 琉球海沟地震带； G 华南沿海地震带； H 台湾西部地震带； I 台湾南-马尼拉海沟地震带； J 南海地震带

由于难以理清广大海域的台站分布和记录能力随时间的变化， 只能通过分析地震目录判断其完整性。常用的方法有G-R关系曲线法(Gutenbergetal.， 1944)和累积地震数-时间曲线法， 二者通过观察曲线的线性程度是否优良来判断某起始震级的地震目录是否完整(黄亦磊等， 2016； 史翔宇等， 2020)。由于G-R关系本身是对数线性关系， 对于小地震的缺失并不敏感(任雪梅， 2011； 徐伟进等， 2014)。同时G-R关系曲线法需要预先假定高质量地震目录的时间起点， 不便于区分不同大小地震完整记录的起始时间(吴果等， 2014)。通过累积地震数-时间曲线法可以直观地观察累积地震数随着时间的变化趋势， 便于判断地震完整记录的起始时间。但累积地震数-时间曲线法也存在缺陷， 当活动水平随时间波动的不同震级档的地震数据混在一起时， 该方法难以加以区分(吴果等， 2014)。因此， 本研究采用分震级档的累积地震数-时间曲线， 即以0.5个震级单位为间隔分档绘出累积地震数-时间曲线， 再判断该震级档地震记录完整记录的起止时间。

各地震带分震级档的完整性分析结果见表1。由于地震带和震级档较多， 受篇幅限制， 本文仅就完整性分析过程中的关键问题进行论述：

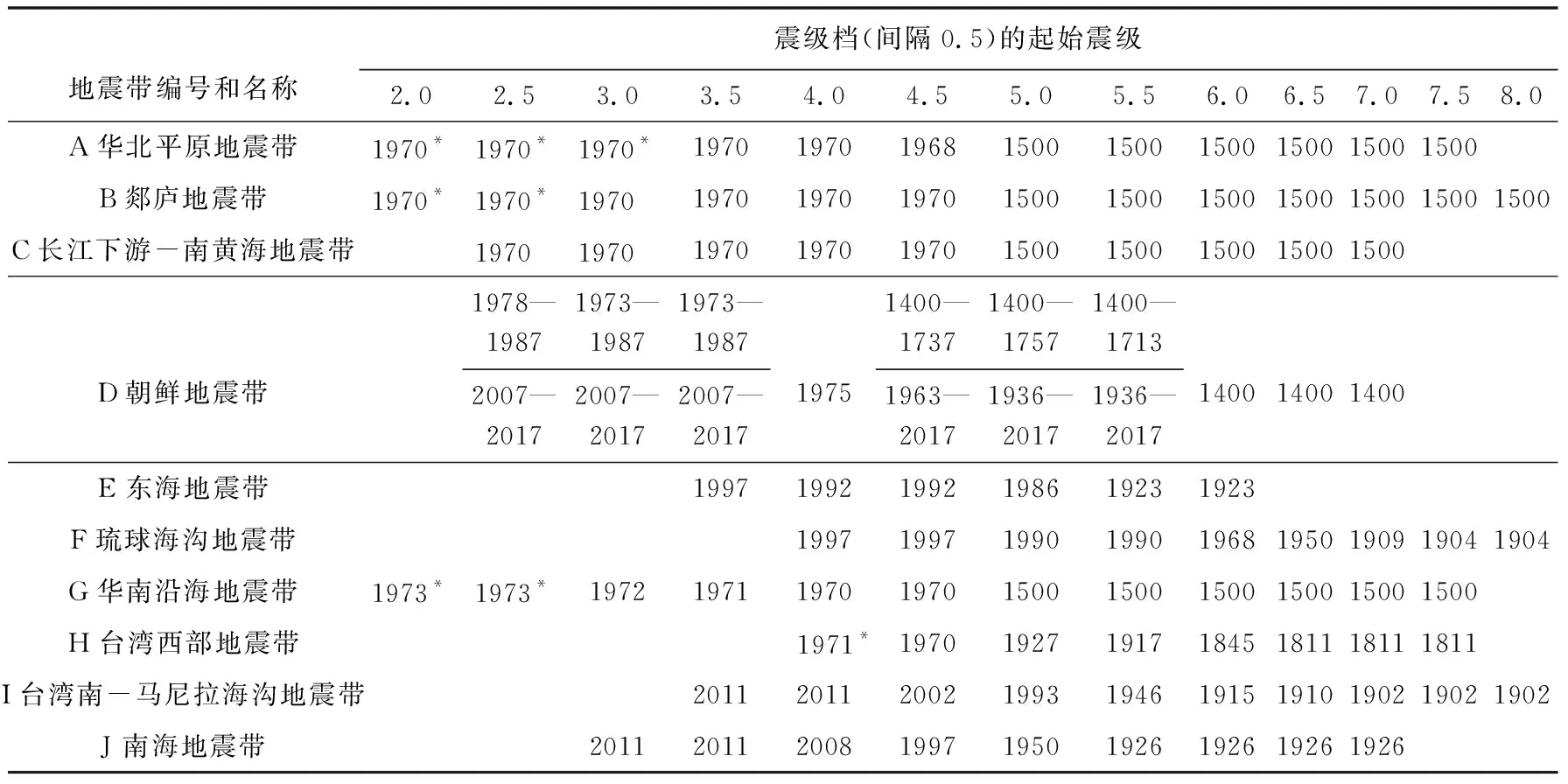
表 1 中国海域及邻区地震带各震级档对应完整记录的起始年份Table1 The start years from which the earthquake catalogs within different magnitude intervals are completely recorded for the seismic zones in China seas and adjacent regions

(1)总体而言， 大陆内部或近海的地震带历史地震记录悠久， 仪器地震记录大致始于1970年后， 如华北平原地震带、 郯庐地震带、 华南沿海地震带等； 远海的地震带缺乏历史地震记录， 且仪器地震数据完整记录的时间很短， 如东海地震带和南海地震带， 这与台网的布设时间以及密度、 精度直接相关。

(2)地震目录的截止时间为2018年10月， 故2018年的地震记录尚不完整， 因此表1 中默认的截止时间是2017年。华北平原地震带、 郯庐地震带、 华南沿海地震带以及台湾西部地震带的小震级档存在2010年以后数据不全的现象。本文以华北地震带M2.5～2.9的数据为例予以展示(图3a)。该现象与中国地震台网中心不再公布部分地区2010年后的小地震数据有关(Chenetal.， 2006)。

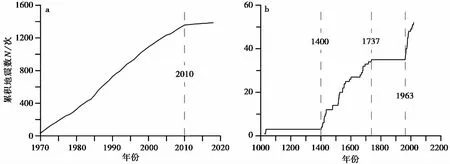
图 3 分震级档的累积地震数-时间曲线Fig. 3 The curve of cumulative number of earthquakes versus time for a magnitude interval.a 华北平原地震带M2.5～2.9； b 朝鲜地震带M4.5～4.9

(3)华北平原地震带、 郯庐地震带、 长江下游-南黄海地震带和华南沿海地震带M≥5.0的地震记录从1500年以来记录完整(表1)， 该结果与黄玮琼等(1994)、 潘华等(2006)和徐伟进等(2014)的分析结果基本一致。

(4)如图3b 所示， 朝鲜地震带的M≥4.5地震记录的完整记录时间最早可以追溯到1400年， 这一判断与翟文杰等(2004)的工作一致。此外， 朝鲜地震带的地震目录在1737—1963年约200a间缺少M4.5～5.9的地震记录。假设地震活动服从泊松分布， 则可以估算出该现象属于正常地震活动水平波动的概率约为10-31， 属于极低概率事件。因此， 可初步判定该现象是由于地震记录不完整或数据收集不充分导致的。然而， 由于本文采用的算法具有很大的灵活性， 同一震级档对应2个乃至更多个完整记录时段的数据仍然可被有效利用。

(5)随着震级增大， 高震级档的地震数逐渐减少， 给完整性分析带来困难。因此， 对于同一地震带， 依据高震级档的完整记录起始时间不晚于相对低的震级档的原则予以约束。

观察表1 可知， 不同地震带或不同大小的震级档对应的完整记录时长差异巨大， 若想要模型充分地利用有限的地震记录数据、 增加样本量， 对上述分震级档的地震目录进行完整性分析是很有必要的。

1.3 地震活动参数拟合

基于上述地震目录完整性分析结果， 采用Weichert(1980)提出的方法计算各个地震带的a值和b值(式(1))及b值的标准差(式(2))。该方法可利用不同震级档对应不同完整时段的地震数据(吴果等， 2019)。

(1)

(2)

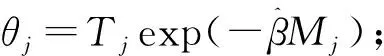
各地震带的地震活动参数拟合结果见表2， 表中Mmin为拟合参数时使用的地震数据的震级下限； 各地震带的震级上限Mmax主要参考中国第5代地震动参数区划图(潘华等， 2013)和高战武等(2021)的工作， 同时结合地震目录中记录到的最大历史地震对其进行调整。

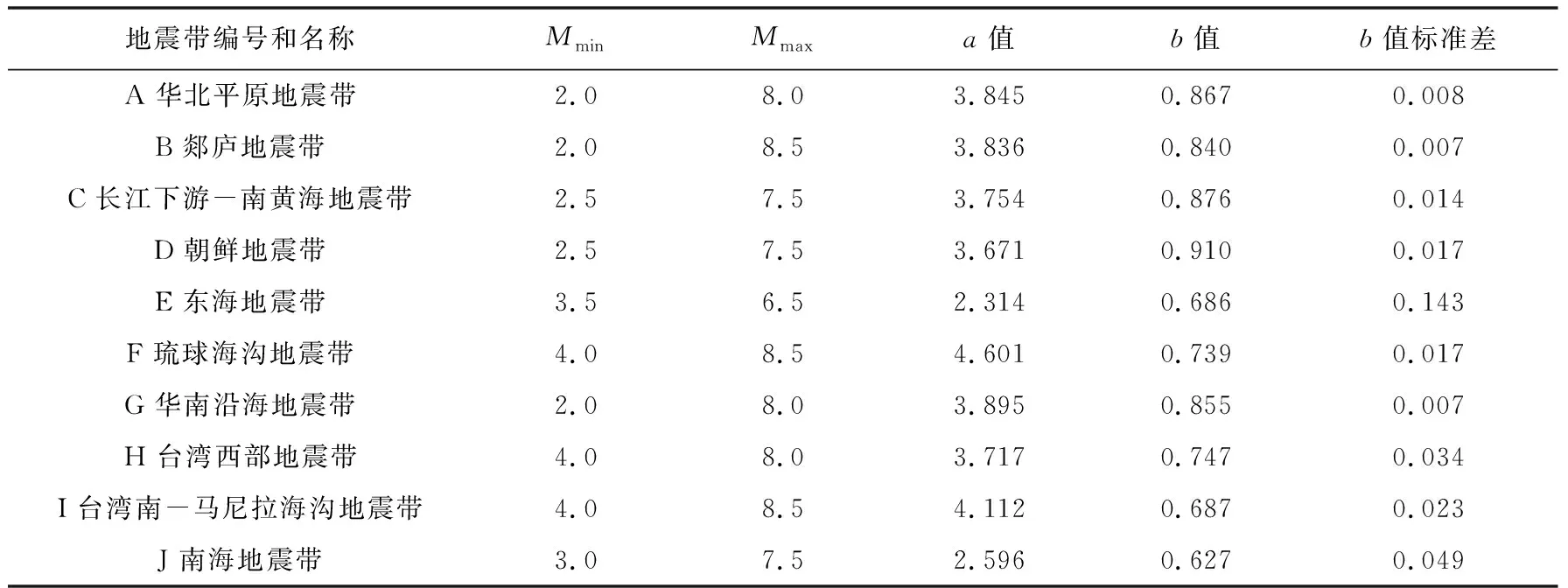
表 2 中国海域及邻区各地震带的a值、 b值及b值的标准差Table2 Parameters including a-value， b-value and the standard deviation of b-value for each seismic zone

2 自适应空间平滑模型原理

ASSM与传统的SSM都属于空间平滑模型， 二者的基本原理相同， 都是利用已经发生的中小地震的分布预测未来的地震分布， 在一定程度上类似于国内常用的地震“原地重现”理论。但空间平滑模型主要针对没有明确发震构造背景的中小—中强地震， 与“原地重现”理论存在一定差异。此外， 地震不可能绝对精确地“原地重现”， 未来地震的发生位置具有很大的不确定性。已有的地震密集或者稀疏的地区只能相应地代表该地区未来发生地震的可能性更大或者更小， 具有概率含义。因此， ASSM和SSM都需要利用空间平滑函数将记录到的中小地震发生率向震中附近平滑分配， 使地震发生率的高低变化在研究区内呈现平滑过渡的趋势， 而不是简单地“落”在已有地震记录的位置上。前人已对上述理论的可靠性进行了验证(Kafkaetal.， 2000)， 同时ASSM在CSEP计划中的优异表现也可看作是对该理论可靠性的重要检验(Straderetal.， 2017； Schorlemmeretal.， 2018)。

广大海域地区缺乏大陆地区丰富的地震地质、 地球物理探测等多学科研究数据， 地震目录是开展其地震活动性研究最重要的基础资料。同时， 如图 1 所示， 广大海域地区地震分布十分不均， 例如两大海沟俯冲带地震分布的密集程度远超过东海和南海地区。因此， 考虑到ASSM模型是目前国际上应用十分成功的基于地震目录的地震活动模型， 且能充分体现地震分布密集程度的空间变化， 本研究在中国海域及邻区建立ASSM模型具有一定的合理性和应用价值。

基于前文的地震目录完整性分析和地震活动参数拟合的结果， 进一步采用Wu等(2019)改进的自适应空间平滑算法建立ASSM模型， 下文将简述其原理。

2.1 学习目录和检测目录

ASSM与SSM的最大区别在于ASSM将整个地震目录划分为2部分(图 4)， 第1部分为学习目录(Learning catalog)， 第2部分为检测目录(Testcatalog)。首先用学习目录建立模型， 再用检测目录中的地震评价预测效果， 从而实现参数优化。学习目录中的地震并非都能被利用， 在使用前要采用各个震级档对应的完整记录时段对其进行筛选(表1)， 筛选后的地震可称为输入地震(Input earthquakes)。国际上最新的地震危险性分析研究一般将起算震级定为M5.0(Petersenetal.， 2015)， 因此本研究将检测目录的目标震级Mt定为M5.0， 即用检测目录中M≥5.0的地震测试模型的预测效果。

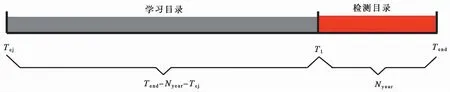
图 4 自适应空间平滑地震活动模型中的学习目录和检测目录划分示意图Fig. 4 Schematic diagram of the division of learning catalog and test catalog in adaptively smoothed seismicity model.

2.2 空间平滑函数

将研究区网格化， 网格大小设为0.1°×0.1°， 然后采用空间平滑函数将学习目录中的输入地震发生率向四周的网格平滑分配以预测未来的发震概率分布。本文采用应用最为广泛的高斯平滑函数：

(3)

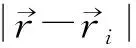
2.3 输入地震对地震年发生率的贡献

式(3)中默认每个输入地震对研究区内地震年发生率的贡献相等。为了改进模型的地震预测效果， 需要尽可能充分地利用有限的地震数据， 扩大样本量。然而如表1所示， 不同地震带、 不同震级档的地震记录来自不同时长的完整记录时段， 如果不对式(3)加以调整， 则输入地震不再符合原有的震级-频度关系， 得到的模型也不合理。

为了解决上述问题， 需要求出每个输入地震对研究区内地震年发生率的贡献v(i)。假设地震i属于震级档j， 那么v(i)为

(4)

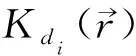
(5)

利用G-R关系可以将最小输入地震震级Mmin以上地震的年发生率转化为任意目标震级Mt以上地震的年发生率：

(6)

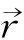
(7)

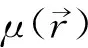
(8)

式中，Nyear为检测目录时长， 一般为5a或10a。

2.4 平滑半径

ASSM与SSM的另外一大区别在于对平滑半径的取值方式不同。传统方法中， 同一震级档的地震记录都采用相同的平滑半径(Frankel， 1995)。而ASSM中每个输入地震i的平滑半径di均取决于其周边地震的密度， 衡量标准是地震i到第n个最近地震的水平距离(Helmstetteretal.， 2007； Werneretal.， 2011)。因此， 当选定任意n时， 地震密集区的平滑半径较小， 地震稀疏地区的平滑半径较大。

然而， 如前文所述， 本研究中不同地震带和震级档的地震都可能对应不同的完整记录时长， 因此需要对求取平滑半径的算法做相应调整： 令地震i的平滑半径bi等于以地震i的震中为圆心的圆的半径， 要求该圆内的所有地震的年发生率的和等于设定值RS， 本文将RS称为周边地震年发生率。计算时由小到大尝试不同的RS值， 依次计算出模型结果并评价其优劣， 最终选取令模型表现最优时的RS作为最终值。确定RS后， 即可相应地计算出每个输入模型的地震i的平滑半径bi， 其平均值为

(9)

式中，Ni为输入地震总数。

2.5 模型优化和概率增益函数

采用前人推荐的概率增益函数对模型的优劣予以评价(Kaganetal.， 1977； Helmstetteretal.， 2007； Werneretal.， 2010)。假设每个网格内地震的发生过程服从泊松分布， 均值为μ′(ix，ii)(式(8))， 那么在检测目录相同的时间段内网格(ix，iy)中发生n个地震的概率为

(10)

假设研究区内所有网格都恰好发生检测目录中该网格记录到的地震数， 对其发生概率取对数似然函数：

(11)

引入一个空间均一模型(Lunif)作为参考， 在该模型中发震概率在研究区内均匀分布， 类似于美国国家地震区划图中的背景地震模型(Frankel， 1995)。将检测目录中震级大于目标震级Mt的地震数Nt除以研究区的网格数Ntg即可得到空间均一模型网格的地震发生率。

最终， 模型的优劣可通过概率增益函数G体现，G越大则对应模型表现越优， 选取使G达到最大时的周边地震年发生率RS作为最终的参数设置。G的形式为

(12)

3 模型计算结果及分析

为了检测不同参数设置对模型的影响， 基于上述原理建立了不同的模型， 模型参数和检测结果见表3， 表中展示了该参数设置下概率增益函数G最大时的结果。选取2013—2017年共5a的目录作为检测目录， 目标震级Mt定为M5.0， 目标震级以上地震数Nt共87条。学习目录中的地震最早可追溯到1400年， 对应朝鲜地震带历史地震记录的完整记录起始时间(表2)。学习目录的截止时间为2012年， 与检测目录之间互不重叠。

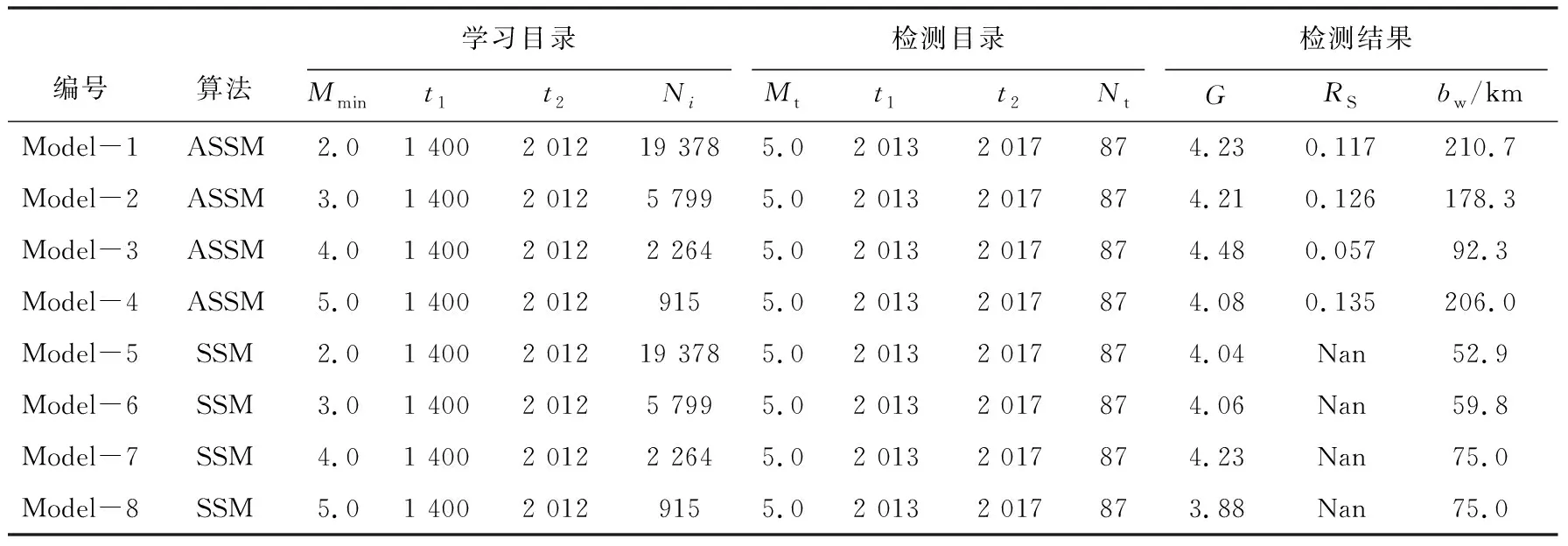
表 3 不同参数设置下模型预测结果的对比Table3 Forecast results for models with different parameter settings

3.1 输入地震最小震级

模型Model-1、 Model-2、 Model-3和Model-4对应的学习目录输入地震最小震级Mmin分别为M2.0、M3.0、M4.0和M5.0(表3)。Mmin越小， 输入地震数Ni越多， 随着Mmin的减小Ni从915条增长为19378条。其中表现最优的是Model-3， 对应的G值为4.48。事实上，G值与周边地震年发生率RS直接相关。上述模型的G值随RS变化的曲线如图 5 所示。4条曲线的总体趋势均为： 随着RS增大，G值较为快速地增大， 随后G值增加速率逐渐减小直至达到最大值， 然后G值开始缓慢下降。

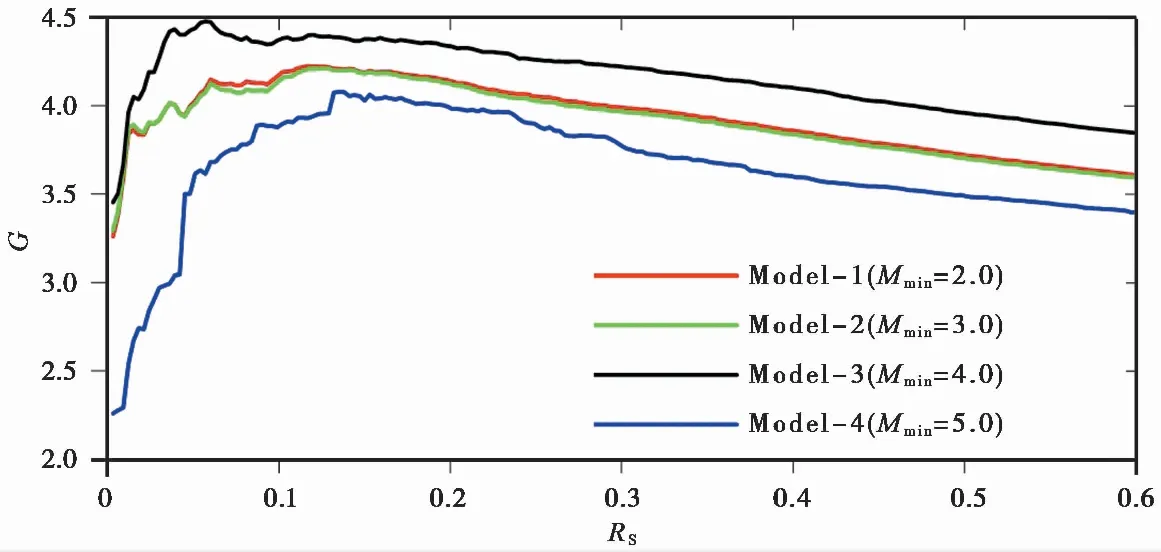
图 5 不同模型的概率增益函数G随周边地震年发生率RS的变化曲线Fig. 5 The curves of the probability gain per earthquake(G)versus the annual occurrence rate of surrounding earthquakes(RS)for different models.

从图 5 可以看出， Model-3的G值始终占优， Model-1和Model-2居中， Model-4的最差。这说明当模型的Mmin从5.0降低到4.0， 模型的表现显著优化， 这与输入地震数从915提高到2264直接相关。

然而Model-1和Model-2的表现不如Model-3， 这说明对于本研究区而言Mmin并不是越小越好。分析其原因可知： 琉球海沟地震带和台湾南-马尼拉海沟地震带的最小完整震级均为M4.0(表1)， 因此当Mmin为2.0或者3.0时， 这2个地震带并没有增加输入地震数， 反而受到其他地震带小地震过度平滑的影响。同时， 这2个地震带的地震最为密集(图 1， 2a)， 对结果造成影响的权重最大。因此， 建立模型时需要综合考虑研究区内的地震分布和各个地震带最小完整震级的情况。

3.2 ASSM与SSM的效果对比

为了对比自适应空间平滑模型(ASSM)和传统的固定平滑半径的空间平滑模型(SSM)的表现， 建立了4个SSM模型Model-5、 Model-6、 Model-7和Model-8(表3)， 分别与Model-1、 Model-2、 Model-3和Model-4相对应， 区别在于选用了固定的平滑半径。参考美国国家地震区划图的做法(Petersenetal.， 2015)， SSM中对M4.0以下输入地震的平滑半径取50km，M4.0以上输入地震的平滑半径取75km。2类模型的概率增益函数G的对比见图 6， 图中输入地震最小震级Mmin逐步从2.0上升到5.0， ASSM的G值始终大于SSM， 这说明ASSM相比SSM具有稳定的优势。

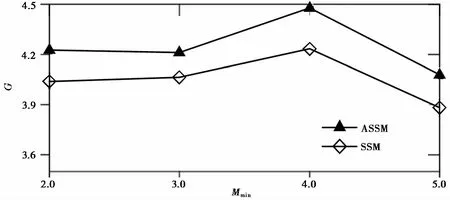
图 6 ASSM和SSM的概率增益函数G随输入地震最小震级Mmin 变化的曲线Fig. 6 The curves of the probability gain per earthquake(G)of ASSM or SSM versus the minimum input magnitude(Mmin)of the learning catalog.

3.3 最终模型

经过上述对比分析， 选取Model-3作为本研究的最终模型， 该模型采用M4.0以上的地震数据建立模型， 对应的周边地震年发生率RS为0.057， 所有输入地震的平均平滑半径bw为92.3km。Model-3预测的M≥5.0地震的年发生率分布见图 7。

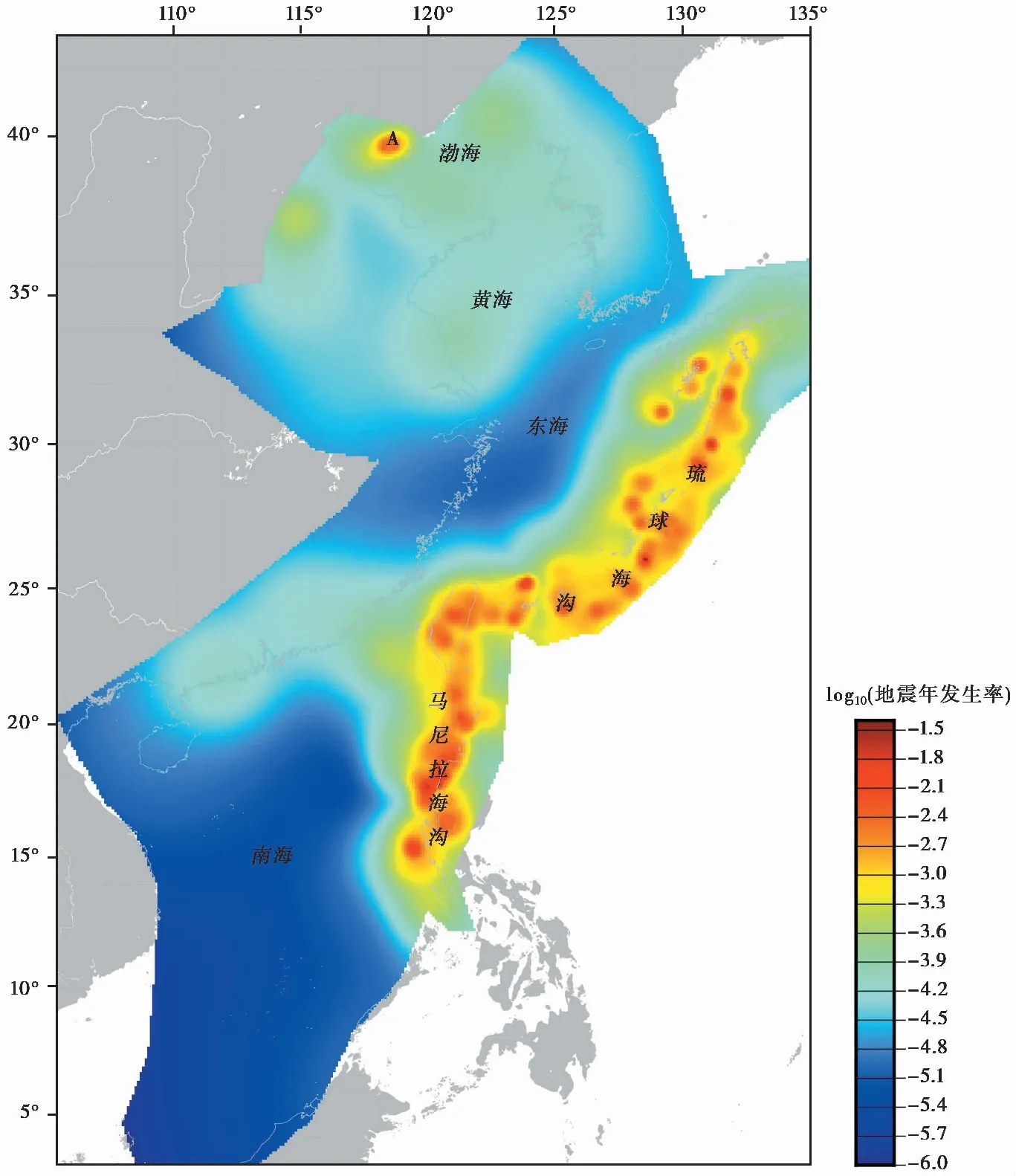
图 7 M5.0以上地震的年发生率预测结果(表3中的Model-3)Fig. 7 Forecasted seismicity rates of M≥5.0 annually in each cell from Model-3 in Table 3.

观察图 7 和图2a可发现， 图 7 中地震年发生率的高低变化与图2a中地震分布的密集程度一致， 同时地震年发生率由高到低平滑过渡。年发生率最高的地区位于琉球海沟、 中国台湾、 马尼拉海沟一带， 这源于该地区的俯冲带背景； 其次是华北平原地震带的北段， 其中一处显著高于周边地区(图 7 中的A区)， 这是由于1976年唐山地震后有大量余震出现(万永革等， 2008； 蒋长胜等， 2013)， Gardner等(1974)提出的除丛算法无法完全有效识别； 渤海、 黄海、 朝鲜半岛的地震活动水平与广东、 福建沿海一带接近， 浙江沿海、 东海和南海的地震活动水平最低。

3.4 模型的优点和局限性

本文的ASSM模型的主要优点有：

(1)本模型完全基于历史和仪器地震记录数据， 可以非常方便快捷地建立模型， 并且ASSM的地震预测效果已得到了前人研究的证实(Straderetal.， 2017； Schorlemmeretal.， 2018)。

(2)本模型在利用地震数据时具有较强的适用性和灵活性： 通过对算法进行调整， 完整记录水平随时间和空间变化的地震数据都可以被本文的模型充分利用。当遇到类似于朝鲜地震带的情况， 即同一个震级档有2个以上完整记录时段(图2b， 表1)， 在式(4)中扣除记录水平较差的时段的时长即可， 这在程序中很容易实现。

(3)本文的ASSM与传统的SSM相比， 预测效果具有稳定的优势。最新的美国国家地震区划图也从单独使用SSM改为同时使用ASSM和SSM(Petersenetal.， 2015， 2020)。

本文的ASSM模型的不足和局限性有：

(1)本模型只能给出目标震级Mt以上的地震年发生率， 不能给出震级上限， 而震级上限是地震活动和地震危险性分析中的重要参数。

(2)本模型基于历史和仪器地震记录数据， 不能体现活动构造、 地球物理、 大地测量等学科的研究成果， 例如断层的空间分布、 滑动速率、 闭锁程度等(程佳等， 2020)。近年来CSEP的研究发现， 同时考虑地震目录和活动断层等多种资料和手段的混合模型的预测效果要优于单一的预测模型(Rhoadesetal.， 2018； Taronietal.， 2018)， 因此建议在进行地震危险性分析时将本模型与其他模型相结合使用。

(3)大地震的能量积累和释放具有一定的时间相关性(Matthewsetal.， 2002； Lietal.， 2017)， 而本文的ASSM模型假设网格内地震的发生服从时间泊松分布， 属于时间独立的地震活动模型。

4 结论

通过建立中国海域及邻区自适应空间平滑地震活动模型， 并比较不同参数设置时模型的表现， 得到以下几点结论：

(1)通过算法的调整， 本文的模型可以充分利用完整记录水平随时间和空间变化的地震数据， 显示出较强的适用性和灵活性。

(2)当输入地震最小震级设为M4.0时模型的表现最优。这提示建立模型时并非输入地震最小震级越小、 地震数越多， 模型的表现就越好， 而是需要综合考虑研究区内地震的分布情况和各个地震带的完整记录水平。

(3)本模型与传统的固定平滑半径的平滑模型相比具有更大的概率增益函数值， 这种优势不受模型的输入地震震级的影响。

(4)本文的模型存在不能计算震级上限和反映断层分布、 未能考虑大震复发的时间相关性等不足和局限性。因此， 本模型可以单独用于描述中小—中强地震的发震概率， 也可作为确定潜在震源区的空间分布函数的重要因子之一。但在进行地震危险性分析时， 建议结合地震地质、 GPS等其他学科的成果形成混合模型， 从而进一步提高模型的适用性和有效性。本文的工作将为中国海域地震危险性分析和建模提供依据。