人民币利率互换定价研究——基于Ho-Lee模型实证分析

乔克林，罗 钧

（延安大学数学与计算机科学学院，陕西延安 716000）

标准利率互换合约是合约双方在相同名义本金额以及相同货币下一方支付固定利率，一方支付浮动利率，利率互换的意义在于为合约双方提供各自所需的利率支付方式，利率互换的定价结果对于互换双方是一个重要的参考指标。目前为止，标准利率互换依旧在场外市场上流行。在标准的利率互换合约中，一方向另一方支付在今后指定的若干年或者若干月下名义本金按浮动利率所产生的现金流，同样的，这一方将会收取相同时间内和相同名义本金上按固定利率产生的现金流。利率互换的意义在于减少双方的融资成本和规避利率波动带来的风险，并使双方获得自己想要的支付方式［1］。从2006—2021年，人民币利率互换已经经历了长达15年的发展，利率互换的定价问题一直都是研究的重点内容。对利率互换交易的合理定价，是利率互换交易中的关键环节，是利率互换交易顺利完成的保障，也能够在一定的程度上活跃交易量，增强利率互换市场的流动性，使得利率互换的定价效率提高，从而优化了资源配置。利率互换的定价主要受利率波动的影响，所以用哪一种方法去估计利率的波动是利率互换定价的前提。

为了更好的去研究利率的动态变化，研究者提出了均衡模型和无套利模型。均衡单因子模型一般假设短期利率服从的过程是平稳的，从而确定收益率曲线的形状，其研究代表包括VASICEK等［2］、COX等［3］及CHAN等［4］，均衡模型可以近似地匹配今天的利率期限结构，但无法完全匹配。而无套利模型以收益率曲线作为输入变量可以做到完全匹配，无套利模型对于利率衍生品定价效果更好，无套利模型的代表包括HO等［5］、BLACK等［6］、HULL等［7］、HEATH等［8］给出的模型。国内的学者在无套利模型的基础上对利率互换以及利率互换的应用进行了研究，黄佐钘等［9］利用利率互换对套期保值进行了研究，刘承承［10］系统的对人民币利率互换定价问题进行了研究。

然而国内学者关于Ho-lee模型的定价过程以及定价结果研究较少，而且没有将Ho-Lee模型应用到互换付息周期较短的利率互换定价中。本文基于Ho-Lee模型对6个月期的SHIBOR_3M利率互换进行定价分析，其结论进一步对其他几种定价模型的比较提供了分析基础，定价日期的选取处在新冠疫情期间，所以能够从定价结果反映出Ho-Lee模型是否具有稳定性。

1 利率互换模型的定价机制及树图结构

1.1 Ho-Lee模型

Ho和Lee提出了一种无套利模型，短期利率满足以下过程：

其中，短期利率的瞬时标准差σ为常数，θ(t)为时间t的函数。变量θ(t)定义了r随时间t移动的平均方向，他与r的大小无关，其中

其中，F(0，t)为时间0所观察的在时刻t的瞬时远期利率［11］，t∈[t j，t j+1](j=0，1，…，N-1)，令F(0，t)=f j，其中t j+1=t j+Δt，下标t表示对于t的偏导数。

1.2 建立基于Ho-Lee模型各期限的利率二叉树结构图

在该模型下，每期的波动率可以由（3）式得出：

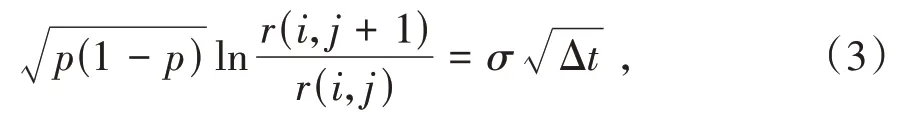
其中，r(i，j)表示在节点(i，j)时的短期利率，p表示利率上升的概率，1-p表示利率下降的概率，Δt表示上个支付日到下个支付日间隔的时间。本文假设在这个模型之中利率上升的概率都是0.5，利率下降的概率也都是0.5，将其带入（3）式能够得到（4）式：

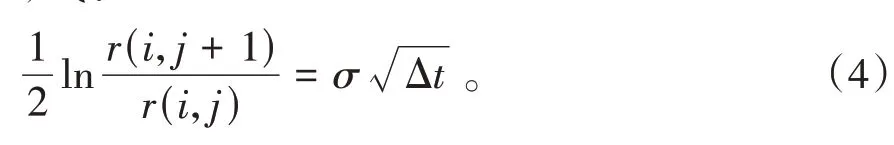
（4）式等式两边同时取以e为底的指数就可以得到（5）式：

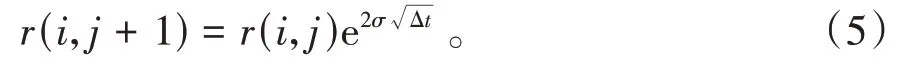
所以，若r(i，j)一旦确定，则r(i，j+1)就可以由（5）式计算出来，r(i，j)是由两期零息债券通过二叉树贴现计算出来，因为在金融市场中不存在套利机会，所以贴现后的价格等于债券的市场价格，通过二叉树计算出r(i，j)以及r(i，j+1)，这样得出来的r(i，j)与r(i，j+1)就能够匹配第一期的零息债券的收益率。上述第一期利率二叉树［12］构建如图1所示。

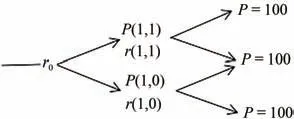
图1 第一期利率二叉树结构图

图1中P(1，1)和P(1，0)分别是通过模型得出的零息债券贴现到第一时期的上升价格和第一期下降时的价格，P为100元，因为零息债券的终值为100。其中P(1，1)和P(1，0)的贴现过程如下：

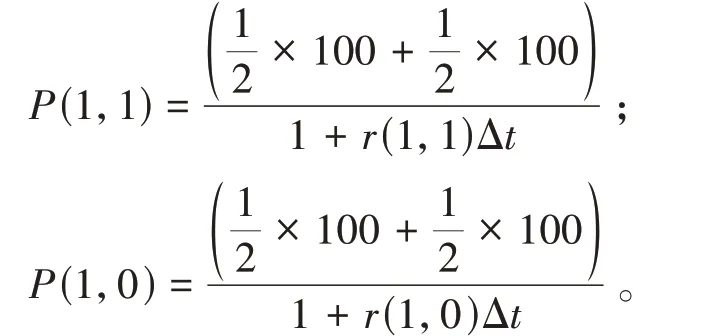
期初的价格P0可以由P(1，1)和P(1，0)继续贴现，从而有

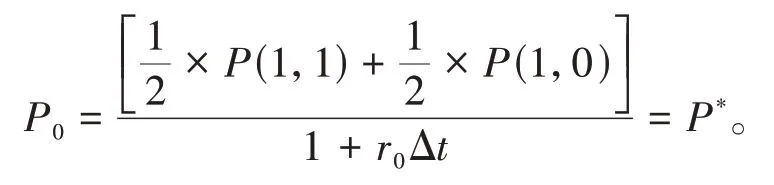
因为是无套利模型，所以不存在套利的机会，那么由零息债券的终值所贴现到起初的价格P0必然与零息债券实际的期初价格P*相等，通过上述公式，就可以计算出满足条件的r(1，1)，r(1，0)。

下面用同样的方法构建第二期利率二叉数结构图，如图2所示。

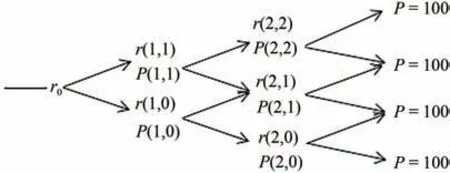
图2 第二期利率二叉树结构图

利率上升的概率和利率下降的概率都为0.5。r(2，2)为在第一期支付日上升且在第二期支付日也上升的利率，r(2，1)为是第一期支付日上升但第二期支付日下降或者第一期支付日下降但第二期支付日上升的利率，r(2，0)表示的是第一期支付日和第二期支付日都下降的概率。

由（4）式可以得到

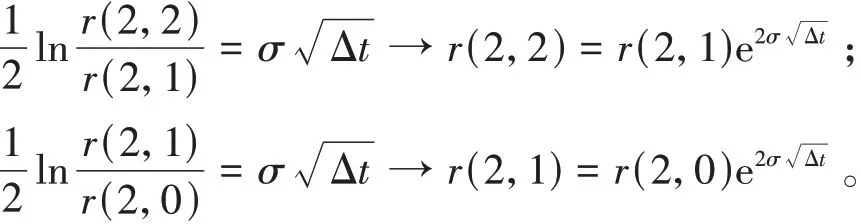
从而，如果能够计算出r(2，1)，那么r(2，2)，r(2，0)就可以计算出来。并且可以得出r(2，2)，r(2，1)，r(2，0)三者之间的关系：

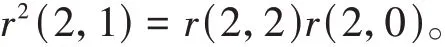
借鉴之前的方法，可以用如下的计算过程得到第二期的各个利率。

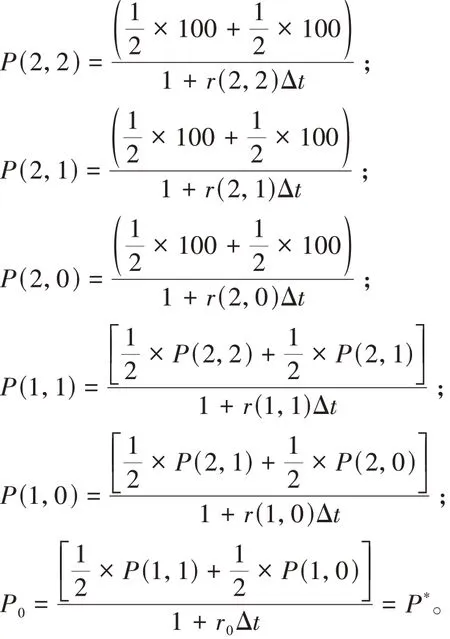
之前通过第一期二叉树已经计算出来了r(1，1)和r(1，0)，再通过上面的式子可以求出r(2，0)，r(2，1)，r(2，2)。

同样的方法，可以构建第三期利率二叉数结构图，如图3所示。

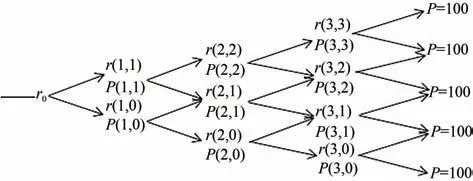
图3 第三期利率二叉树结构图

根据（4）式可以得到

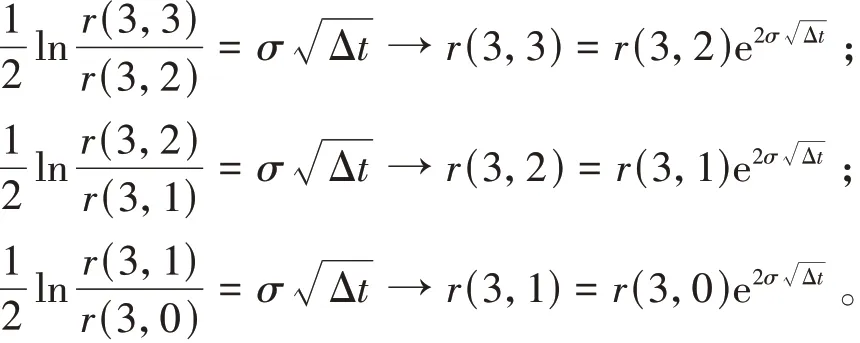
从而如果计算出其中一个利率，那么其他两个利率就可以算出来了。可以计算出多期二叉树的远期利率，算出每个状态的远期利率后，就可以对利率互换进行定价，因为是无套利定价模型，对互换本金进行浮动利率也就是用得出的远期利率贴现恰好等于固定利率贴现的现值，从而可以得出固定利率。

2 实证分析

2.1 估计波动率公式

其中，Si为基于SHIBOR各期限利率在i天末的值，ui为第i天的连续复利收益率。

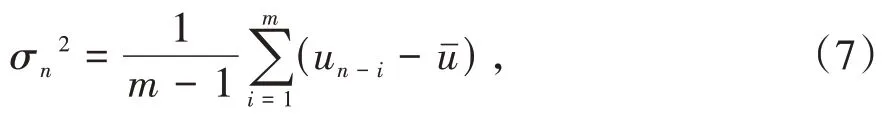
其中，σn为第n-1天所估计的基于SHIBOR各期限利率在第n天的波动率，σn2为日方差率。

其中，为ui的平均值。

2.2 利率互换定价公式

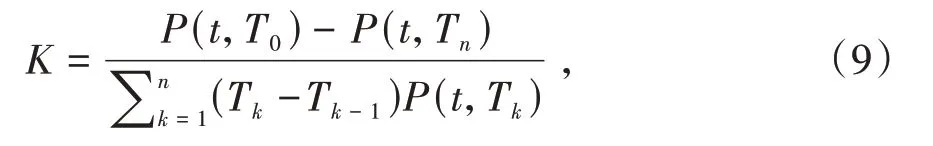
其中，K为固定利率也就是利率互换的价格，P(t，T k)表示在随机利率下的第k期的折现因子，T k为到期日，T k-T k-1是两个支付期的间隔时间，以年为单位。

2.3 数据的选取

利率互换以FR007和SHIBOR_3M作为基准利率的交易量最多，所以本文选用中国货币网公布的SHIBOR数据来确定利率期限结构，运用Ho-Lee模型对6个月期的SHIBOR_3M利率互换进行定价，定价结果同公布的当日利率互换的成交价格进行比较分析。

本模型设定不考虑违约风险，要对利率互换进行定价，就要知道互换合约的内容，包括参考利率、固定利率、浮动利率、交易日、起息日以及到期日等等。一个标准的6个月期的SHIBOR_3M利率互换合约如表1所示。

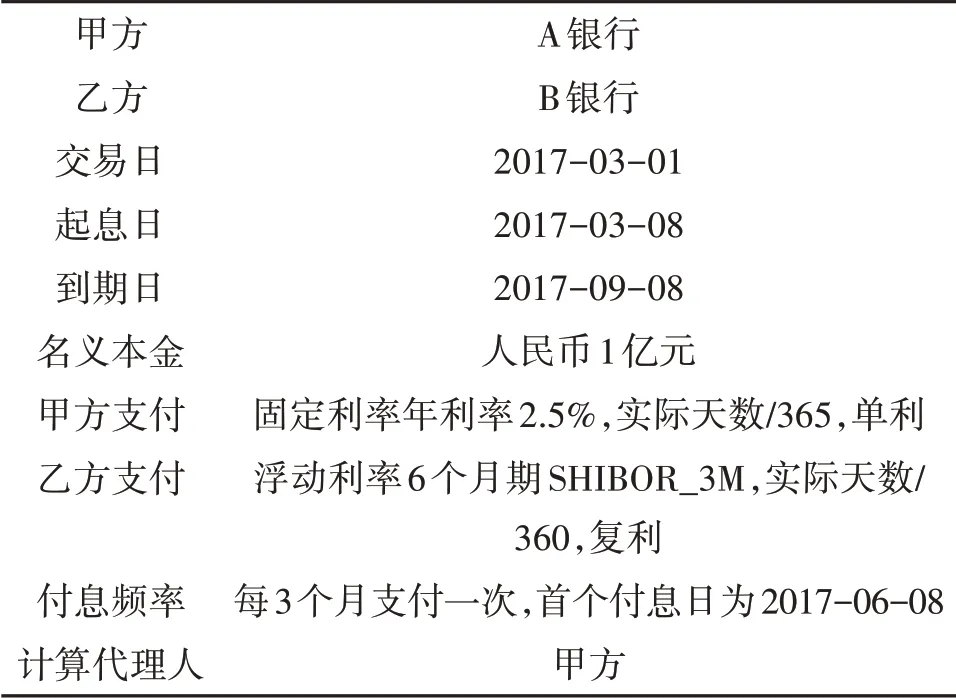
表1 [13]6个月期的SHIBOR_3M利率互换合约

6个月期的SHIBOR_3M利率互换每3个月交换一次利息，浮动利率为每3个月重置一次。需要知道每个付息日的利率期限结构，本文选取了2021年6月10日—2021年9月3日共60 d的SHIBOR期限数据结构分别对当日的6个月期SHIBOR_3M利率互换进行定价。表2列出了2021年8月31日—2021年9月3日的有关数据。

表2 SHIBOR期限数据结构

2.4 Ho-Lee模型的实证分析

利用Ho-Lee模型进行定价时需要知道各个利率的年化波动率，由于Ho-Lee模型中的波动率是一个不与时间有关的常数，所以为了反映6个月期SHIBOR_3M利率互换中短期利率的波动率，本文假设在SHIBOR_3M利率互换交易日时，就已经确定了SHIBOR_3M利率互换中短期利率的波动率，6个月期的SHIBOR_3M利率互换各期限波动率是用该日前60个交易日的计算数据得到，一年中的交易日为250 d。本文选取2021年6月10日—2021年9月3日60个交易日的数据，用以下方程求得年化波动率：

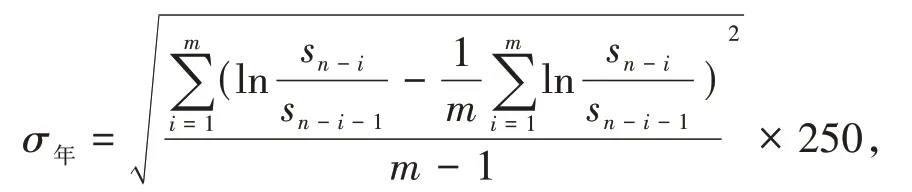
其中，n为SHIBOR_3M利率互换中短期利率的波动率的起始日期，以天为单位，S n-i是在n天以前的有关利率数据。表3列出了2021年9月3日与2021年9月2日的有关数据。

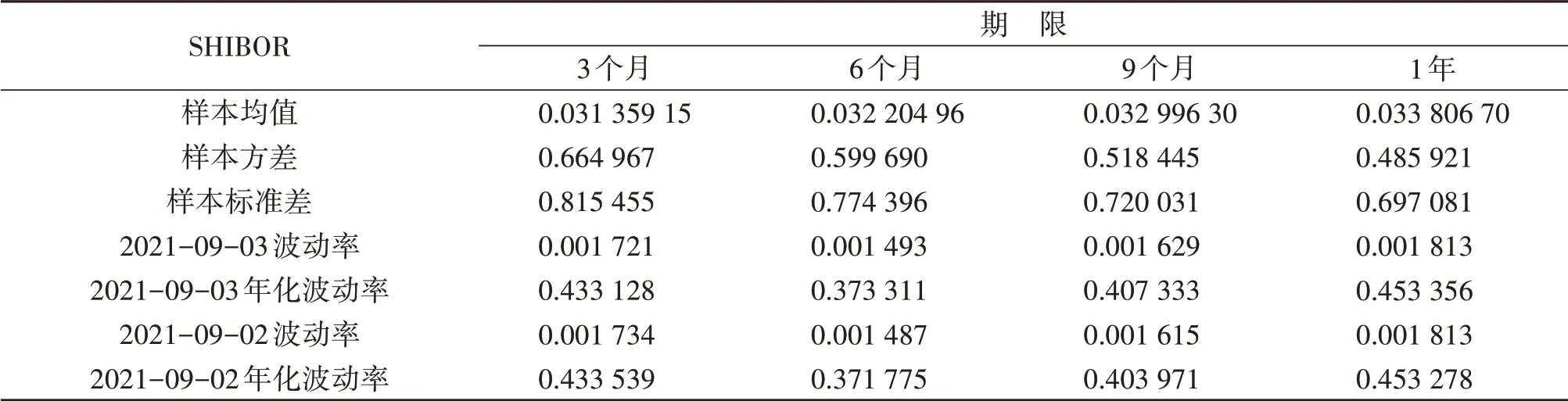
表3 年化波动率

这样就得到了2021年9月3日与2021年9月2日的年化波动率。下面使用Matlab［14］编程，基于Ho-Lee模型来构造利率二叉树，得到每个时间点的远期利率，从而利用公式计算出利率互换的固定利率值。结果如表4所示。由表4可以看出来，Ho-Lee模型的定价结果与实际成交价格在短期时间内没有巨大的差异，但是在价格趋势的变化上来看有所不同。这是因为由于数据有限，本文假设选取的由国家发行的贴现债券发行价格在不同的日期是固定不变的，所以导致了9月3日的定价结果与成交价格相对偏差较小，而其他时期与成交价格相对偏差略大的情况，还有一个原因就是Ho-Lee模型中的波动率为常数，也就是不同时间下利率互换的利率波动率相同，然而这在现实情况中可能性很小。

表4 Ho-Lee模型成交价格与定价结果比较

3 结束语

Ho-Lee模型在基于6个月期的SHIBOR_3M利率互换中定价结果较成交价格误差较小，可以给投资者一个很好的参考。本文只是基于Ho-Lee模型对短时间的利率互换合约进行定价，不过此模型在一年期或者一年期以上的定价结果还需要验证。无套利模型下还有其他几种模型，定价出来的结果可以相互比较进行分析，并在这个基础上继续完善模型，使模型在特殊的时间段比如疫情期间也有一个很好的表现。