NL-fuzzy拓扑空间与L F完备映射

王延军

（延安大学数学与计算机科学学院，陕西延安 716000）

在文献［1］中，先由分子网的收敛定义了普通集X上的N-开集，再由N-开集定义了N L-fuzzy拓扑空间，最后在fuzzy集上定义fuzzy完备映射。文献［2］中定义了N紧空间，并研究了N紧空间的性质。文献［3-14］从不同层面对fuzzy拓扑空间或Lfuzzy拓扑空间中相关问题进行了讨论，并得到了一些好的结果。如在N-fuzzy拓扑空间中任一映射f：X→{x}是fuzzy完备的，NL-fuzzy拓扑空间X到T2空间Y的连续映射也是fuzzy完备的等等。本文将这一结果合理的推广到L-fuzzy拓扑空间中，定义了新的NL-fuzzy拓扑空间与L-fuzzy完备映射，简称L F完备映射。讨论了NL-fuzzy拓扑空间与L-fuzzy拓扑空间之间的关系，证明了L F完备映射在Lfuzzy拓扑空间中与N L-fuzzy拓扑空间中的许多性质。从而丰富了已有的结果。

在本文中L表示fuzzy格，X表示非空集，L X表示X上的全体L F集。f：L X→L Y指L值Zadeh型函数，1X和0X分别表示L中的最大元和最小元。A′与-A分别表示A的伪补与闭包，M(L)表示L中全部分子之集，M∗(L X)表示L X的全体分子之集，其他未说明的概念、记号和术语请参见文献［1-10］。

1 预备知识

定 义1.1［2］设(L X，δ)是L-fuzzy拓 扑空 间，A∈L X，φ∈L X称为A的α-远域族，如果对于每一个LF点xα∈A，有P∈φ使得xα∉P，φ称为A的α-远域族，如果存在λ∈β∗(α)使得φ是A的λ-远域族，这里α∈M(L)，β∗(α)是α的标准极小集。

定 义1.2［2］设(L X，δ)是L-fuzzy拓 扑空 间，A∈L X，称A为N紧集，如果对于A的每一个α-远域族有有限子族构成A的α-远域族。当1X是N紧的，称(L X，δ)是N紧空间。

定义1.3［2］设(L X，δ)是L-fuzzy拓扑空间，L X中的分子网是一个映射S：D→M∗(L X)，记为S={S(n)，n∈D}，D是一个定向集。

2 N L-fuzzy拓扑空间

定义2.1设(L X，δ)是L-fuzzy拓扑空间，xα∈M∗(L X)，A∈L X且为N紧集。如果xα∉A，则称A为xα的N紧远域，记xα的所有N紧远域之集为Nη(xα)。

定义2.2设(L X，δ)是L-fuzzy拓扑空间，S是L X中的分子网，xα∈M∗(L X)。

1）称xα为S的N极限点，或称S为N收敛于xα，如果对于每一个P∈Nη(xα)，S最终不在P中，并记作S的一切N极限点记为NlimS。

2）称xα为S的N聚点，或称S为N聚于xα，如果对于每一个P∈Nη(xα)，S经常不在P中，并记作。S的一切N聚点记为NadS。

由定义2.1和定义2.2不难证明下面的定理2.1：

定理2.1设(L X，δ)是L-fuzzy拓扑空间，S={S(n)，n∈D}是L X中的分子网，xα∈M∗(L X)，则

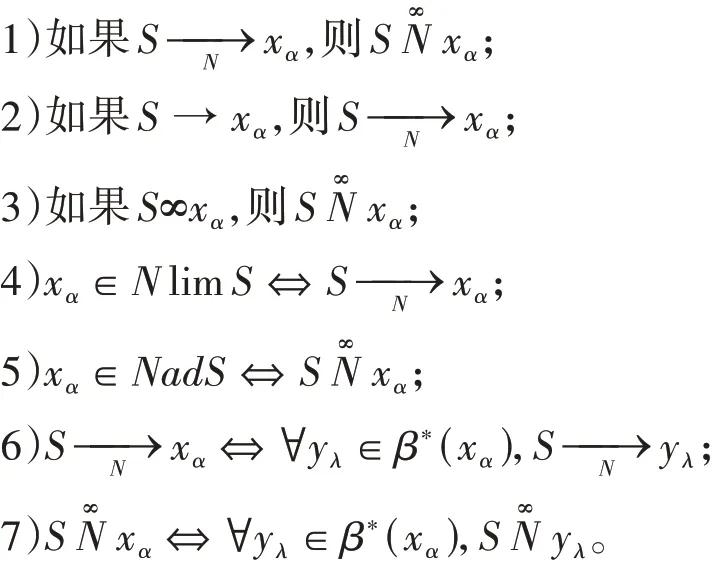
定理2.2设(L X，δ)是L-fuzzy拓扑空间，S={S(n)，n∈D}是L X中的分子网，xα∈M∗(L X)，则

1）当且仅当存在S的子网T使得

证明1）“⇒”设S={S(n)，n∈D}是L X中的分子网，xα∈M∗(L X)且，对∀n∈D及∀P∈Nη(xα)，存在k∈D使得S(k)∉P，且k≥n。取k=N(n，P)，有映射N：D×Nη(xα)→D。由于S(N(n，P))∉P，故令E=D×Nη(xα)，定义(n1，P1)≥(n2，P2)当且仅当n1≥n2，P1≥P2。对∀(n，P)∈E，E是定向集，取T(n，P)=S(N(n，P))，则T={T(n，P)，(n，P)∈E}是S的子网，且

“⇐”设T={T(m)，m∈E}是S的 子 网，且由子网的定义知存在映射P：E→D且m，m0∈E，当m≥m0时，对∀n0∈D有P(m)≥n0。由于，故存在m1∈D，当m≥m1时，对∀P∈Nη(xα)有T(m)∉P。于是存在m2∈E，当m2≥m0，m2≥m1时，有T(m2)∉P且P(m2)≥n0。取n=P(m2)，S(n)=S(P(m2))=T(m2)∉P，且n≥n0，则S经常不在P中，所以。

2）由定理2.1的2）直接可得。

定义2.3设(L X，δ)是L-fuzzy拓扑空间，A∈L X，如果A中每一个α分子网S都N收敛于高度为α的某个点，则称A为N开集。若A为N开集，则A′为N闭集。L X中的所有N开集构成的拓扑称为N L-fuzzy拓扑，记为Nδ，称(L X，Nδ)为N L-fuzzy拓扑空间。

定理2.3设(L X，Nδ)为NL-fuzzy拓扑空间，则(L X，Nδ)是L-fuzzy拓扑空间。

证明1）显然0，1∈Nδ；

2）证明若A，B∈Nδ，则A∧B∈Nδ。

设M是A∧B中的任一α分子网，则M既是A中的α分子网又是B中的α分子网，即且由定义2.2知，一方面对∀P∈Nη(xα)，M最终不在P中，另一方面对∀Q∈Nη(yβ)，M最终不在Q中，取R=P∧Q，则R∈Nη(xα)∧Nη(yβ)，M最终不在R中，故A∧B∈Nδ。

3）证明若∀t∈T，A t∈Nδ，则∨t∈T A t∈Nδ。

设U是∨t∈T A t中的任一α分子网，则存在t0∈T使得A t0∈Nδ且U是A t0中α分子网，故U将N收敛于高度为α的某个点，于是∨t∈T A t∈Nδ。

推论2.1设(L X，Nδ)为NL-fuzzy拓扑空间，则L X中的所有N闭集构成NL-fuzzy余拓扑。

证明设A为N开集，则A中每一个α分子网S都N收敛于高度为α的某个点。由定义2.3，则A′为N闭集。从而L X中的所有N开集构成的拓扑为N Lfuzzy拓扑，故L X中的所有N闭集将构成N L-fuzzy余拓扑。

推论2.2设(L X，Nδ)为NL-fuzzy拓扑空间，则(L X，Nδ)中的常值L F集是开集。

证明由定义2.3和推论2.1可得。

3 LF完备映射

定义3.1设(L X，δ)和(L Y，τ)是2个L-fuzzy拓扑空间，称映射f：L X→L Y为LF完备映射，如果f是LF连续的、闭的且对∀B∈L Y，f-1(B)是L X中的N紧集。

定理3.1设(L X，δ)和(L Y，τ)是2个L-fuzzy拓扑空间，f：L X→L Y为L F完备映射，且(L X，δ)是T2空间，则下列条件等价：

1）f是LF连续的、闭的且对∀B∈L Y，f-1(B)是L X中的N紧集；

2）f是LF连续的、闭的且对∀B∈L Y，f-1(B)是L X中的f紧集；

证明因为(L X，δ)是T2空间，故N紧⇔f紧，从而1）⇔2）。又因为是L F连续的、闭的，故1）⇔3）。于是1）⇔2）⇔3）。

定理3.2设(L X，δ)和(L Y，τ)是2个L-fuzzy拓扑空间，f：L X→L Y为L F连续映射，则下列条件等价：

1）f是LF完备映射；

2）对于每一个分子网S，如果则

证明类似于文献［1］中定理4.2的证明，可证得。

定理3.3设(L X，δ)、(L Y，τ)及(L Z，σ)都是Lfuzzy拓扑空间，如果f：L X→L Y与g：L Y→L Z都为LF完备映射，则g∘f是LF完备映射。

证明因为f与g都是LF完备映射，故f是LF连续的、闭的，g是L F连续的、闭的。于是由LF连续映射的性质知g∘f是LF连续的，从而g∘f是闭的。另一方面，对∀B∈L Z，g-1(B)是L Y中的N紧集，而(g∘f)-1(B)=f-1(g-1(B))，设C=g-1(B)，则C∈L Y，因为f是L F完备映射，所以f-1(C)是L X中的N紧集，即g∘f是LF完备映射。

定理3.4设(L X，δ)和(L Y，τ)是2个L-fuzzy拓扑空间，f：L X→L Y为L F完备映射，A∈L X且是闭集，则f|A：L A→L Y为L F完备映射。

证明由定义3.1可以直接得证。

推论3.1设(L X，δ)和(L Y，τ)是2个L-fuzzy拓扑空间，f：L X→L Y为LF完备映射，B∈L Y且是闭集，则f|f-1(B)：L f-1(B)→L Y为L F完备映射。

证明由定义3.1和定理3.4可得。

定理3.5设(L X，δ)和(L Y，τ)是2个L-fuzzy拓扑空间，f：L X→L Y为LF完备映射，如果(L X，δ)是T2空间，则(L Y，τ)也是T2空间。

证明设(L X，δ)是T2空间，S={S(n)，n∈D}是L X中的α分子网，则f(S)是L Y中的α分子网，且由于f是LF完备映射，则S有子网T={T(m)，m∈D}且f(T)是f(S)的子网，由文献［3］中的定理5.2.12知|supp(limS)|≤1。于是由定理2.2的2）可得故|supp(limf(S))|≤1，从而(L Y，τ)是T2空间。

定理3.6设(L X，δ)和(L Y，τ)是两个L-fuzzy拓扑空间，f：L X→L Y为L F完备映射，如果对∀A∈L Y且A是N紧集，则f-1(A)是L X中的N紧集。

证明设S={S(n)，n∈D}是f-1(A)中的α分子网，则f(S)是A中的α分子网，又因为A∈L Y且A是N紧 的，所 以由 定 理3.2有。于是f-1(A)是L X中的N紧集。

推论3.2设(L X，δ)和(L Y，τ)是两个L-fuzzy拓扑空间，f：L X→L Y为满的LF完备映射，如果(L Y，τ)是N紧的，则(L X，δ)是N紧的。

证明由定理3.6直接可得。

定理3.7设(L X，Nδ)为NL-fuzzy拓扑空间，则f：L X→{x}是L F完备映射。

证明由N L-fuzzy拓扑空间的定义知f-1(x)是L X中的N紧集，而f：L X→{x}是连续的、闭的，由定义3.1知f：L X→{x}是L F完备映射。

定理3.8设(L X，Nδ)和(L Y，Nτ)是2个满层的、T2的NL-fuzzy拓扑空间，若f：L X→L Y为L F连续映射，则f是L F完备映射。

证明因为(L X，Nδ)和(L Y，Nτ)是满层的、T2的N L-fuzzy拓扑空间，从而它们也都是L-fuzzy拓扑空间，故如果A∈L X，且A是N紧集，则A是闭的。所以由定理3.6知，对∀B∈L Y且B是N紧集，则f-1(B)是L X中的N紧集。于是f-1(B)是闭的。故f是闭的，所以f是LF完备的。

定理3.9设(L X，δ)和(L Y，τ)都是N紧的、T2的L-fuzzy拓扑空间，则f：L X→L Y为LF连续映射当且仅当f是LF完备映射。

证明“⇒”由定理3.9直接可得。

“⇐”由LF完备映射的定义直接可得。