基于SARIMA-LSTM的 零售生鲜品库存需求预测

熊芷瑶 李林

摘  要：针对零售业的生鲜类商品存在易损耗、货架周期短、明显的季节性等特点，提出一种新的组合预测模型。采用SARIMA-LSTM组合模型综合供应商、零售商、用户三方面考虑需求影响因素如准时交货率、综合成本、气温状况、销售金额等，并结合贝叶斯优化算法对LSTM进行超参数选择，将SARIMA的模型预测值和实际值间的误差序列进行修正并得到预测值。实验证明，考虑需求影响因素的组合预测模型比单一传统统计方法的预测精度要高，并对以后零售业库存管理有一定的建设意义。

关键词：SARIMA;LSTM;组合预测模型;贝叶斯优化算法;库存需求预测

中图分类号：F253    文献标识码：A

Abstract： Aiming at the characteristics of fresh goods in retail industry， such as easy wear and tear， short shelf cycle and obvious seasonality， a new combination forecasting model was proposed. The SARIMA-LSTM portfolio model integrated suppliers， retailers and users demand three aspects to consider factors such as on-time delivery rate， comprehensive cost， the temperature condition， the sales amount， etc.， and combined with bayesian optimization algorithm for super LSTM parameter selection， the SARIMA model error between the predicted value and actual value sequence modification and predictive value. The experimental results show that the combined forecasting model considering the demand influencing factors has higher forecasting accuracy than the single traditional statistical method， and has a certain construction significance for the future retail inventory management.

Key words： SARIMA; LSTM; combination prediction model; bayesian optimization algorithm; inventory demand forecast

0  引  言

库存需求预测指根据物料历史库存需求状况来预测未来的需求量，属于库存管理中重要的一部分。随着近几年零售市场库存物料种类繁多，生命周期短，库存需求预测越发困难。尤其是生鲜类商品，它有着极大的消耗需求，同时本身具有易损耗、易变质等特点，其库存控制是需在短时期内立即做出决策判断的，因此及时准确的预测库存需求变得越发困难。

对于库存需求量时间序列预测方面，主要包括统计方法和机器学习两大类。比较经典传统的统计方法有加权平均法、指数平均法、灰色预测[1]等。后来渐渐出现机器学习在预测方面的应用，如BP神经网络[2]、前馈神经网络与蝙蝠算法和缩放共轭梯度算法结合[3]提高了传统神经网络的学习能力和预测结果的精度。近年来，单一的预测模型不能满足复杂的库存需求，逐渐出现考虑需求特性或需求影响因素的预测模型以及组合预测模型。龚巍[4]在库存需求预测不仅考虑了电力物资的包括重要性、紧急性等需求特性，并且运用GA-BP组合预测模型最终实现动态库存控制。Elcio， Tarallo等[5]运用机器学习在短保质期和易腐产品在预测方面的好处，降低零售店的库存率。

本研究提出基于SARIMA和LSTM的组合预测模型，并且将领域专家的意见和生鲜类商品库存的特性结合起来。考虑需求影响因素成为预测变量的一部分，应用该模型对零售生鲜类商品做出库存需求预测，并通过H零售企业的生鲜品每月库存需求量進行验证。

1  理论方法

1.1  SARIMA预测模型

ARIMA全称为差分移动平均模型，通常被记作ARIMAp，d，q。p表示自回归项数，d表示让时间序列平稳差分的次数，q表示移动平均项数。

ARIMA模型的数学表达式如下：

X=λX+λX+…+λX+μ+φμ+φμ+…+φμ                            （1）

其中：X是平稳变量，λ是自回归项系数，μ是残差，φ是移动平均项系数，δ是常数项，ω是白噪声序列，也称为残差。

SARIMA是建立在ARIMA模型基础之上的，考虑了其季节性元素，形式为ARIMAp，d，q×P，D，Q，S，其中p为非季节性回归项数，d为非季节差分阶数，q为非季节移动平均项数，P为季节性回归项数，D为季节性差分阶数，Q为季节性移动平均项数，S为季节性时间跨度[6]。

本文的研究对象为零售企业生鲜类商品，具有明显的季节性特征，因此拟用ARIMAp，d，q×P，D，Q，S进行建模预测。

1.2  LSTM预测模型

LSTM是一种特殊的RNN，具有记忆数据序列的长期依赖关系，有着强大的自学习能力和非线性拟合能力[7]。如图1所示，LSTM模型结构中各单元的更新方式如下：

图1中，x表示该时刻的数据信息，激活函数σ、tanh表达式通常取如下值：

σx=                      （2）

tanhx=                      （3）

f表示遗忘门，能够过滤前序时刻的状态信息，识别前序时刻对后序时刻的影响程度;i表示输入门，用来控制输入信息进入本时刻信息的比例;o表示输出门，用于控制本时刻状态信息输出的比例，计算公式分别为：

f=σ

W

h，

x

+b                                         （4）

i=σ

W

h，

x

+b                                         （5）

o=σ

W

h，

x

+b                                         （6）

其中：W、W、W均是权重矩阵。如公式（7）所示，c表示本时刻状态信息，其值由本时刻输入信息以及上一时刻状态信息决定：

c=f×c+i×                                             （7）

其中：=tanh

W

h，

x

+b。h表示本时刻隐藏层的状态信息：

h=o×tanh

c                                              （8）

1.3  贝叶斯优化算法

贝叶斯优化算法能够在每次迭代中，根据代理模型拟合实际目标函数的结果选择最优评估点，减少目标函数的迭代次数，可提高模型泛化能力并避免过拟合现象。

贝叶斯优化算法的迭代过程分为三部分：根据最大化采集函数选择最优评估点;将评估目标函数加入观测数据;更新目标函数的后验概率分布和采集函数。文中采用高斯过程作为代理函数，期望提高函数为采集函数。

1.4  模型實现及评估方法

研究基于Anaconda环境下的Python语言对SARIMA模型和LSTM神经网络模型进行编程实现。其中，SARIMA模型主要通过调用Statsmodels库进行实现;而LSTM神经网络模型主要通过Tensorflow作为后端，采用Keras进行实现[8]。

关于模型评价，研究选用均方误差MSE、平均绝对误差MAE、平均绝对百分比误差MAPE三个指标来评价这几种模型对于该库存需求的时间序列预测性能，指标数值越小，说明预测精度越高，预测效果越好。这四种评价指标表达式分别为：

MSE=

-y                                          （9）

MAPE=

（10）

其中：y为实际观测值，为预测值，n代表测试集的样本数量。

2  组合模型的建立

2.1  数据描述

本文采用H零售企业2010年至2020年连续11年132个月份的生鲜类商品的库存需求量数据作为基础研究数据。其中前120个的月份数据作为训练集，后12个的月份数据作为测试集。

2.2  组合模型中SARIMA模型建立

2.2.1  序列平稳化

（1）平稳性检验及平稳化处理

根据人们对生鲜类商品的购买习惯，夏季以及全网大促的特定月份会出现非常大的库存需求量，因此存在明显的周期性。将序列的趋势、季节和随机效应分解出来绘制时间序列分解图（图2）。通过ADF检验结果可知，检验统计量的值为0.73，并且在90%、95%和99%的置信度下，检验统计量的值均大于对应的临界值，所以认为该初始时间序列是非平稳的。因此，需要进行平稳化处理。

对原始的序列作1阶12步差分来提取原序列的趋势效应和季节效应，由差分后的ADF检验结果可知，1阶12步差分后的序列是平稳的。

2.2.2  模型识别及定阶

通过网格搜索遍历参数的不同组合，利用AIC准则评价选取最优模型参数。所得AIC值最低为286.84时，模型为ARIMA1，1，1×1，1，1，12。

2.2.3  模型拟合及检验

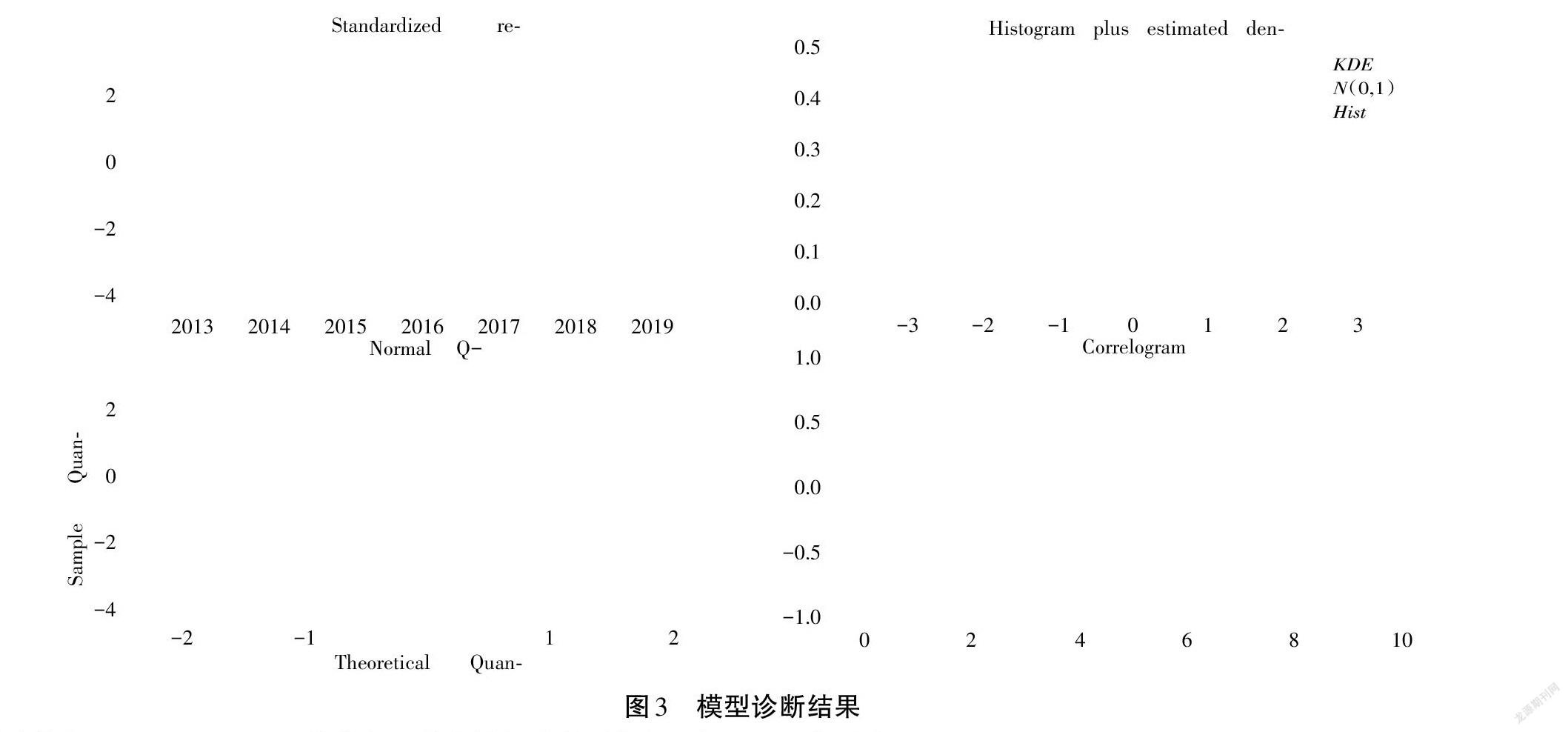
根据拟合结果每个变量的P值均小于0.01，MSE=1.88，MAE=0.9025，MAPE=2.001%，因此可以认为拟合的模型是合理的。然后对残差采用LB检验法进行白噪声检验，检验结果显示Q统计量的P值均大于0.05，拟合模型已经充分提取了时间序列中的信息。最后对残差的分布进行模型诊断，诊断结果如图3所示，残差分布较为正常，时序图基本稳定，服从正态分布且自相关图中不存在自相关。综上，该模型ARIMA1，1，1×1，1，1，12拟合效果很好，具有较好的预测性能。

2.3  组合模型中LSTM模型建立

将上文SARIMA模型的残差指标、准时交货率、零售综合成本、销售金额以及气温状况共五个指标作为LSTM模型的输入变量，预测2020年中12个月的SARIMA模型的残差指标。

2.3.1  数据归一化

当激活函数为sigmoid或者tanh时，需要把数据标准化，此时LSTM比较敏感。因此采用sklearn.preprocessing模块中的最大最小值标准MinMaxSealer

函数将每一维的特征映射到指定区间——0到1之间。

2.3.2  模型训练

LSTM神经网络模型包含三层：输入层、LSTM层、输出层，其中LSTM层包含三层LSTM模块进行训练，最后加一层普通的神经网络用于输出结构的降维。其中超参数运用贝叶斯优化算法进行选择，迭代次数设为50次。其中超参数及取值范围如表1所示。

3  算例分析

3.1  SARIMA时间序列预测

将2020年12个月份的库存需求量进行回代预测，得到预测图如图4所示。其中MSE=5.0035，RMSE=2.2369，MAE=1.7205，MAPE=3.85%。所得预测值与实际值进行相减，得到的残差作为后续LSTM模型的输入变量之一，对残差进行修正。

3.2  LSTM残差修正

利用上文中SARIMA模型的2020年12个测试样本所得的残差序列进行考虑需求影响因素的LSTM神经网络模型预测。由图5验证误差迭代图所示，利用贝叶斯优化算法对LSTM模型进行超参数优化得到误差值最优为第30次。

模型预测得到的残差修正值如图6所示。其中各项评价指标分别为MSE=5.72，RMSE=2.39，MAPE=6.22%。

最后，将SARIMA模型预测所得的12个月的预测值与LSTM神经网络的残差预测修正值进行累加，所得最终结果为2020年12个月的库存需求量预测值。最终累加得到的预测值计算出的各项评价指标分别为MSE=4.7862，MAE=1.4797，MAPE

=3.34%。

4  结果分析

为评估提出的方法，实验选取几种主流文献中的传统方法进行对比分析，对比方法包括灰色理论、样条回归、SARIMA、单特征LSTM和多特征LSTM。

以上六种方法所得最终预测结果计算得到的三个误差指标对比如表2所示，以及2020年12个月份的预测结果图如图7所示。

由对比结果可知，灰色理论的整体趋势捕捉较好，但是对于特殊月份的预測精度很差;而通过加入有效输入变量，样条回归模型对部分特殊月份的预测效果较好，但整体的波动趋势并未准确捕捉。单特征LSTM预测模型的预测效果最差，预测精度最低，该模型既未考虑季节因素的影响，也未考虑库存需求影响因素，因此具有较大偏差。考虑了需求影响因素的多特征LSTM预测模型的预测精度明显较高，但是相比加入了季节因子的SARIMA预测模型的预测效果还是要差一些，未准确抓取季节波动规律。SARIMA预测模型考虑到了时间序列的季节效应，整体预测精度显著提升，但对于某些月份的预测还是具有一定差异。而SARIMA-LSTM组合预测模型既考虑到季节性又考虑到需求因素影响，尽管LSTM易发生过拟合现象，但是该组合预测模型中的LSTM模型仅仅对预测残差进行修正，对其整体预测效果影响较小。因此相比其他五种预测模型，该组合模型的预测精度最高。

5  结束语

针对本文零售业生鲜类商品库存需求量时间序列数据，采取的是一种基于SARIMA-LSTM组合预测模型，与传统预测方法不同的是该方法既考虑到了生鲜类商品的季节性特点，还考虑到四点库存需求的相关性较高的影响因素，如准时交货率、零售综合成本、销售金额、气温状况。通过利用SARIMA模型良好地捕捉季节性规律的能力进行预测，然后构建LSTM神经网络模型加入多个影响指标辅助预测SARIMA模型的残差，尽可能地降低LSTM过拟合现象。对比传统预测模型，得到组合模型的预测性能最佳。因此该组合预测方法对于零售业生鲜类商品库存需求量时间序列数据预测具有一定合理性和参考性，利于库存管理和控制，并且对于其他领域的预测具有一定参考性。

参考文献：

[1]  Paul H K H. Forecasting Construction Manpower Demand by Gray Model[J]. Journal of Construction Engineering and Management， 2010，136（12）：1299-1305.

[2]  X G， C L， W X， et al. A Prediction-Based Inventory Optimization Using Data Mining Models： 2014 Seventh International Joint Conference on Computational Sciences and Optimization， 2014[C] // Computational Sciences and Optimization （CSO）， 2014：611-615.

[3]  P M R B， J A N P， M R A C， et al. A bat optimized neural network and wavelet transform approach for short-term price forecasting[J]. Applied Energy， 2018，210：88-97.

[4] 龚巍. 基于需求特性分类的电力物资库存控制与需求预测方法研究[D]. 沈阳：东北大学（硕士学位论文），2013.

[5]  Elcio T， Getúlio K A， Camilo I S， et al. Machine Learning in Predicting Demand for Fast-Moving Consumer Goods： An Exploratory Research[J]. IFAC PapersOnLine， 2019，52（13）：737-742.

[6]  Nari S A， Diane A. A hybrid seasonal autoregressive integrated moving average and quantile regression for daily food sales forecasting[J]. International Journal of Production Economics， 2015，170：321-335.

[7] 王淑平，李敏，杜敏，等. ARIMA與LSTM模型在医院出院人次预测中的比较研究[J]. 公共卫生与预防医学，2021，32（1）：18-21.

[8] 张晓卉，姚婷婷，陈阳，等. 基于Python语言的ARIMA模型在天津市结核病发病率预测中的应用[J]. 中国感染控制杂志，2020，19（7）：634-642.