夏季太湖北岸的波浪组成及演变特征分析

赵巧华 徐嘉 王健健

摘要： 波浪是驱动大型浅水湖泊中水生生态系统演变的关键动力过程。基于太湖北部近岸区的波浪方向谱、同期风速、风向的观测资料，分析了波浪组成及其演变特征。结果表明：太湖北部近岸区的波浪频率谱主要为单峰或双峰型，属于中高频波;风是波浪形成的主要驱动力，风向（或周边地形）对有效波高的调制作用可用三角函数定量表征;风浪的有效波高、谱峰频率及其平均方向与风速、风向的关系证实了太湖北部近岸区的波浪由涌浪和风浪组成，且涌浪占比较高。岸界的反射作用提高了北部近岸区涌浪的比例;涌浪的有效波高随耦合风速（风速、风向的耦合）不仅呈e指数增长，而且有快、慢分化的现象。研究成果有助于提高大型浅水湖泊中近岸区波浪估算的精度，确保水生生态修复效应。

关 键 词： 波浪组成; 风浪; 涌浪; 有效波高; 太湖

中图法分类号：  P642

文献标志码：  A

DOI： 10.16232/j.cnki.1001-4179.2022.03.029

0 引 言

波浪不仅影响着航运，而且也影响水体中的生物-化学过程。波浪通常包含不同子波浪系统  [1-2] ：① 风浪。它的能量主要通过水-气共振或平行流的不稳定性机制摄取于风场，因而风浪的生成、发展与风场密切相关  [3-4] ;② 涌浪。当风浪离开风的直接作用区域，或在风的直接作用区域内风速突然减小或风向骤然改变，岸界对风浪的反射会使风浪演变成涌浪，因而涌浪散布的区域大于风的作用区域。可见，风场与风浪关系密切，而与涌浪的关系相对疏远  [5] 。

基于实验室分析和野外观测，逄勇等通过对波浪切应力、临界切应力的估算，验证了波浪与太湖悬浮物浓度、透明度的关系  [6] ，证实了波浪是大型浅水湖泊中沉积物再悬浮、营养盐内源释放的主要驱动力  [3-4] ，進而可能也是水华频发，久治不愈  [7] 的关键原因之一。为此，诸多学者针对太湖的波浪要素（波高、周期等）进行了大量的观测和模拟分析，揭示了在开阔湖区波浪有效波高随风速呈e指数增长的规律  [4，8] 。但在近岸区，由于岸界的反射、湖底地形的摩擦及风区变化等作用，风速与有效波高的关系弱化  [8] ，使得近岸区波浪的特征和演变规律远比湖心区复杂。范成新等的研究成果显示：在湖流的长期作用下，太湖的沉积物主要分布于近岸区域（尤其是西岸），湖心区的沉积物分布相对较薄  [9] 。可见，揭示近岸区的波浪特征及其演变规律对水生生态修复有重要意义。迄今为止，近岸区波浪与风速之间的定量关系并未得到足够的关注，导致其生态效应常被忽略，进而可能弱化了水生生态修复效果。

就大型浅水湖泊而言，依据波浪的产生机制和演化规律分离近岸区的波浪组成（风浪和涌浪），揭示近岸区波浪的特征和演变规律，提高近岸区波浪参数的估算精度，有利于水生生态系统的精准修复。由于太湖是典型的大型浅水湖泊，它对气象场的响应迅速，因而其中波浪通常属于中高频波  [10] ，与风浪频率较为接近，增加了分离风浪、涌浪的难度。本文拟基于太湖近岸区的波浪方向谱，结合同期风速、风向数据，探究波浪的组成和演变特征，为太湖水生生态修复奠定基础。

1 研究数据与方法

1.1 研究数据

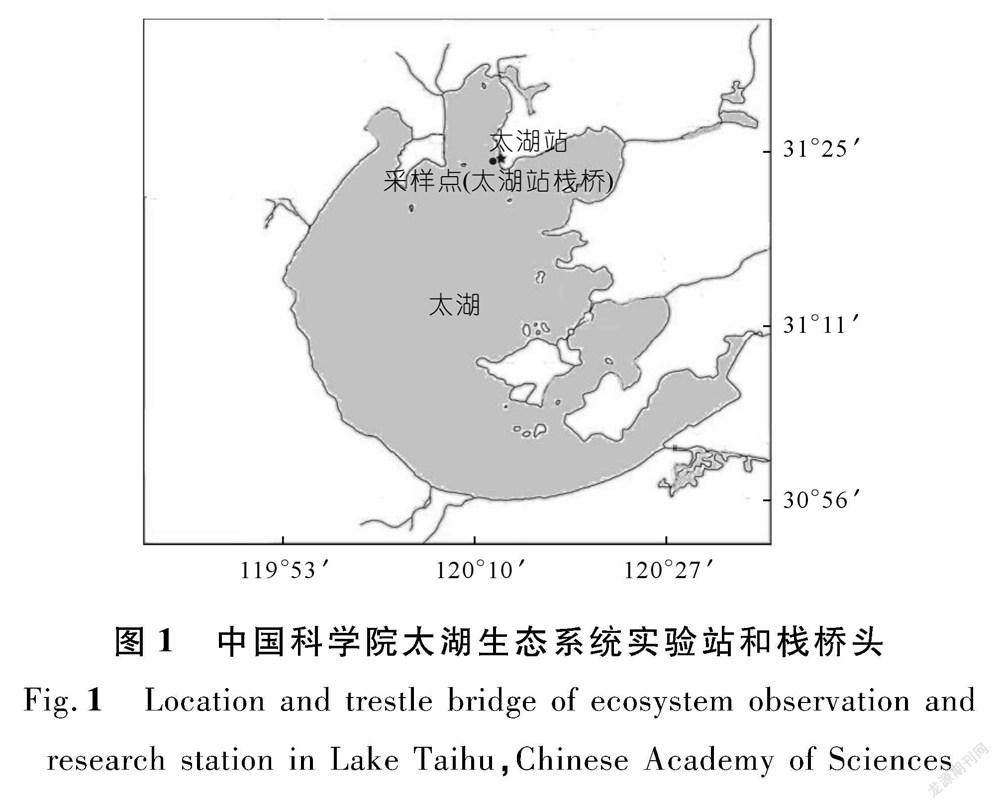
太湖是典型的大型浅水湖泊，面积为2 338 km  2 ，平均水深不超过2 m。波浪的观测点位于中国科学院太湖生态系统试验站的栈桥头（见图1）。

本文所用资料的观测时段为2018年8月21日17：00至9月4日05：00。

利用MIDASDWR方向波浪仪观测波高、波周期等参数，测定频率为8 kHz，每30 min观测一次，观测时间持续10 min。

同期的风速、风向数据来源于中国科学院太湖生态系统试验站的观测资料。风场的观测频率为逐小时，其中正北风向为0（rad），按顺势针方向旋转，正南风向为π（rad）。

为了研究风场对波浪的影响规律，选取整点的波浪方向谱数据和风速、风向资料。

1.2 波浪分离方法

波浪是局地风浪和涌浪的综合，其能量是不同方向、不同频率的波浪分量的总和。本文采用Hanson 和Phillips  [2] 介绍的方法实现波浪分离。 H，F，Θ 分别表示有效波高、谱峰频率及其平均方向，并用下标 w，ww，sw 分别表征观测波浪（综合波浪）、风浪和涌浪。

1.3 非线性分位拟合

由于有效波高是刻画波浪能量的关键参数，是风速、风向等因子的综合反映，在近岸区，风向对波浪的影响尤为突出，但对它的定量描述却一直未能得到有效的解决。为此，本文依据有效波高对风向的敏感特征，采用分位拟合的方式定量表征风向对有效波高的影响。

2 结果与分析

2.1 风场及有效波高的特征

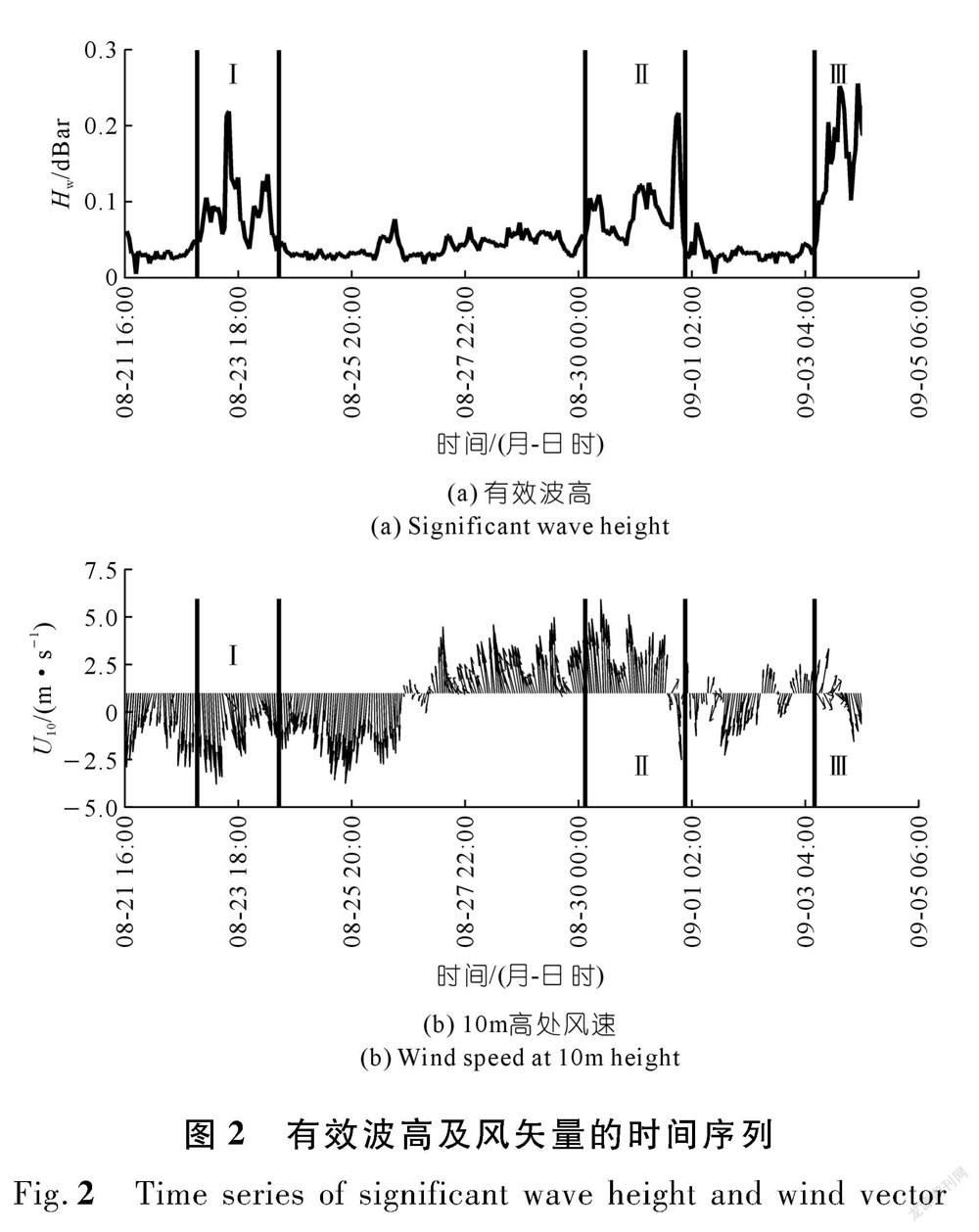
图2（a）描述了有效波高的时序变化。该时序变化包含了3个主要过程（各子图中均已标注）：① 时段为8月23日00：00至8月24日12：00，有效波高呈现三峰状，中峰最强，且右肩峰强于左肩峰（简称Ⅰ过程）;② 时段为8月30日03：00至8月31日23：00，同样也存在三峰，右峰最强且窄（简称Ⅱ过程）;③ 时段为9月3日10：00至9月4日05：00，基本呈两峰（简称Ⅲ过程）。整个观测时段内，最大有效波高为 0.26  dBar左右，平均为0.056 dBar。

从10 km高处风速（ U   10 ）的时序变化来看，平均风速为3 m/s，最大风速为5.8 m/s（见图2（b））。在该时段，受台风（苏力）外围的影响，风速偏大。随着台风逐渐靠近苏南及随后远离、消亡过程中，风速整体偏大。与有效波高的过程相对应，每个过程的波高峰值均对应风速的峰值，但风速的峰值大小并不能完全对应波高峰值的强弱，如Ⅲ过程对应的风速显著小于前两个过程，但波浪峰值却最强。可见，风速是影响波高的关键因子之一。

从观测时段开始至8月26日18：00，风向均偏北，包含了Ⅰ过程（见图2（b））。Ⅰ过程中左峰对应的风速大于最强的中峰所对应的风速;与此类似，8月24日 20：00 至8月26日06：00的风速略大于Ⅰ过程对应的风速，但有效波高基本呈最低值（0.02～0.03 dBar左右），约为Ⅰ过程有效波高的1/10。二者之间的细微差别说明北风或东北风对有效波高影响偏弱，而西北风的影响明显（见图2（b））;Ⅱ过程的西南风、东南风对有效波高影响差别较小。结合观测点的周边地形可以发现，北风或东北风（含东风）的吹程最小，波浪从风场中获得的能量最小，进而说明该风向对有效波高影响远小于西北风和偏南风。可见，风向是影响有效波高的另一关键因素。

2.2 波能频谱特征、风速与有效波高的关系

波能的频谱时间序列刻画了不同频率（ f ）的波能随时间的变化规律，图3中色阶表示波能频率谱 （ S（f） ） 的对数值。为了便于比较，在图3中标注了波浪时序变化的3个主要过程。最大波能基本分布于0.5 Hz的频率附近，而且可以看到在Ⅰ过程至Ⅱ过程过渡期间还有2个相对弱的过程（见图3）。结合波能分布和风矢量变化可以发现，东北风阶段所对应的波能很弱（见图2～3）;除位于0.5 Hz的波能主峰外，某些时段（如Ⅲ过程）位于高频（1.0 Hz附近）处也呈现了次峰：如I过程的中峰及右肩峰;Ⅱ过程中最强的右峰;Ⅲ过程中的两峰;在Ⅰ、Ⅲ过程中的更低频率处，隐约呈现了弱波能分布（见图3）。结合风速、风向的分布特征（见图2）可知，风速、风向是影响波能频率谱呈双峰分布的关键因素。

2.3 风向对有效波高的影响

水体波浪的能量主要来源于风场，其中风区的长短是波能从风场中获取能量多少的关键。本文的观测站点位于太湖北部近岸区，使得周边地形对风区的影响远强于湖心区，可见风向是通过影响风区的方式修正风速对波浪的驱动效应。有效波高是定量表征波能的关键参数，也是波浪对多因子（风速、风浪状态、水深等）的综合响应。因而可通过非线性高分位回归拟合法  [11] 筛选出对风向最为敏感的有效波高样本，进而定量描述风向对有效波高的影响。

由于采样点位于梅梁湾和贡湖湾连接处的北部近岸区，靠近太湖东岸（见图1），从正北向（0 rad）开始，随顺时针旋转，即风向转向东，由于周边地形作用使得风区逐渐变短，导致风能转化为波能减弱，随着风向的持续增大，其风区又逐步延长，风向的限制作用减弱，一直持续到西北向，风向的限制作用才再次逐渐显现出来。可见风向对风区的影响与角度密切相关，且呈周期性，为此采用三角函数的高分位法（95%）拟合有效波高随风向的变化，拟合函数形式为

H w（W d）=a sin （bW d+c）+d （1）

式中： W d为风向，a，b，c，d 为常数。

通过高分位的方法筛选出有效波高对风向敏感的样本，采用三角函数形式拟合有效波高对风向的依赖，拟合效果良好（见图4），说明三角函数可以定量表征风向对有效波高的影响。

2.4 风场与有效波高的关系

依据波浪的组成及其形成机制可知：风浪是由局地风场通过摩擦引起的不稳定或共振方式形成的，因而风浪的有效波高必定与风速呈现密切的相关性，但涌浪通常与局地风场无显著相关性。

采用指数函数形式  [3] 对综合波浪的有效波高（ H  w  ）与风速进行拟合， H  w  与风速之间的确定系数为0.04，说明二者之间无显著的相关性，可见除风速外，另有其他因子影响风速与有效波高关系。此类因素主要有两种：① 风向影响风区的长短，进而调制风能转化波能，从而降低了有效波高对风速的依赖;② 波浪中的风浪、涌浪与风速的关系差异显著，因而波浪中涌浪的比例是影响有效波高与风速关系的另一关键因子。

为此，采用风向对波高的调制形式定量表征耦合风向的风速 W  sd  （简称耦合风速）：

W  sd =U  10 [a sin （bW d+c）+d]/（a+d）

进而利用e指数函数形式拟合 H  w 随W  sd  的變化，发现二者的相关性得到显著的升高，其决定关系 R  2  为0.45（见图5（a））。风速、耦合风速分别与 H  w  相关性的差别说明风向是影响波浪关键要素，风场为波浪能量的主要来源; W  sd  可以有效表征风向、风速的耦合。

为了探究耦合风速对北部近岸区波浪组成比例的影响，选择 W  sd  大于2 m/s的样本与对应的有效波高进行拟合，发现二者之间的关系急剧下降（见图5（b））：结合风向的调制作用， W  sd 越大，风场对波浪的驱动效应增强，综合波浪可能受到边界反射等影响增大，涌浪的比例增加，进而导致其与局地W  sd 相关性急剧减弱。可见，波浪中包含了涌浪;W  sd 与H  w 的相关性及其随W  sd 的变化证实了随着W  sd  的增大，涌浪比例升高。

2.5  风浪有效波高、平均频率及平均方向的特征

风场是太湖波浪产生的主要驱动力，使得波浪中涌浪比例提高，因而通过比较耦合风速 （W  sd ）与风浪的有效波高（H  ww ）、风浪的谱峰频率（F  ww ）及风浪的平均波向（Θ  ww ） 的相关性，探究太湖北部近岸区的波浪组成特征，验证波浪分离方法的有效性。

北部近岸区波浪的 H  ww 随W  sd  的变化与湖心区基本一致，即二者之间呈现e的负指数函数关系，其决定系数（ R   2 ）为0.65（见图6（a））;当 W  sd 大于2  m/s ，W  sd  与相应的 H  ww  的决定系数（ R  2  ）略有降低，其值为0.62（见图6（b））。

通过比较 W  sd 与H  ww 、W  sd 与H  ww  的关系变化（见图5～6），可以发现太湖北部近岸区波浪对耦合风速的响应迅速，风场是太湖波浪的关键驱动因子;岸线的反射等作用使得北部近岸波浪中包含一定比例的涌浪，且涌浪的比例随耦合风速的增大而提高，从而使得当 W  sd  大于2 m/s时， W  sd 和H w 的相关关系急剧下降;同样条件下，风浪的有效波高 （H  ww ）和W  sd  的相关关系证明分离出的风浪中基本未受涌浪污染。波浪分离方法切实可行，且适用于太湖北部近岸区。

风浪的平均频率（ F  ww  ）为1.37 Hz，最大为2.23 Hz，最小为0.42 Hz，并随 W  sd  的增大呈现递减的趋势（见图7）。通常波浪的能量主要集中于波峰; F  ww  远大于波浪的谱峰频率，是对快变风场特征的响应  [12] 。通常风浪的能量直接获取于风场，获取的能量一方面弥补于高频处的能量耗散（湍流、波浪破碎等）;另一方面通过非线性作用向低频传输，促进波浪的发展，使得其频率降低。诚然，当从风场中获取的能量不足，低频处的能量同样补充高频处能量损耗，导致波浪的减弱甚至消亡。因而， F  ww 随W  sd  的变化也从侧面证实了波浪分离的有效性。

风浪是由风直接驱动产生的，对风场的响应迅速，因而其波长相对较短，平均方向也与风场方向较为接近。观测点离岸界较近，且岸界基本围绕在观测点的正北到东南方向（见图1），因而在岸界对波浪的反射作用下，观测波浪中涌浪比例提高。波浪方向与风场方向接近反向，因而从正北到东南方向，波浪方向与风场基本成负相关;随着风向角度的继续增大，岸界离观测点的距离逐渐加大，岸界对风浪的反射作用基本消失，涌浪比例偏低，因而观测的综合波浪方向与风向接近，二者呈正相关（见图8（a））。从风浪平均方向与风向关系来看，二者呈线性关系，其决定系数为0.57，绝大部分样本均围绕在拟合直线周围（见图8（b）），但也存在少量的样本偏离该直线。这些少量样本对应的风向在正北（0 rad）附近，波浪方向也接近2π rad（见图8（b）），其中0 rad和2π rad的方向实际上是围绕在正北向附近，说明上述样本的风向和风浪的平均方向也呈线性关系，即分离出的风浪平均方向与风向基本一致，这也证实了波浪分离方法适用于北岸区。总之，从风场与风浪的谱峰频率、平均方向及有效波高的关系3个方面，证实了耦合风速为波浪的关键驱动因素，岸界的反射作用造成北部近岸区波浪中含有较高比例的涌浪，同时也从风浪方向、频率等方面证实了波浪分离的方法适用于太湖。

2.6 涌浪特征及其与耦合风速的关系

波浪平均方向和风向的关系证明北部近岸区的波浪组成中包含了涌浪，为此有必要探究涌浪的特征及其对耦合风速的响应规律。

图9描述了涌浪的有效波高 H  sw 随W  sd  的变化，该图呈现了两典型特征：①  H  sw 随W  sd  呈快速升高（简称快变趋势）;②  H  sw 随W  sd  呈缓慢增加（简称缓变趋势）。为此，采用e指数形式的分位拟合，分位数分别为85%和35%，拟合效果良好。快变趋势可能是由于风向偏西南，即观测点波浪受岸界反射叠加作用最强，随耦合风速的增大，岸界反射造成的叠加效应增强，使得 H  sw 随W  sd  快速增长。当风向偏东或北时，岸界的反射作用对观测点影响微弱，因而 H  sw 随W  sd  增长相对偏弱。另外，由于太湖涌浪频率偏高，其涌浪传播过程中的衰减也较低频波快，因而反射传输路程越远，衰减越大，进而凸显快、慢变化趋势的分化。可见，上述原因是导致 H  sw 随W  sd  呈增长趋势分化的關键。

H  sw 和W  sd  之间存在线性关系，两者之间的 R   2 为 0.158 ，远低于 H  ww 、H w分别与W  sd  的关系。尽管涌浪的产生机制导致涌浪与局地风场难以存在显著的相关性，但由于太湖的波浪主要由风场驱动，风场作用于水体表面的吹程较短，使得由于岸界反射等作用形成北部近岸区的涌浪频率偏大，在一定程度上也携带了风场的信息，所以 H  sw 和W  sd  也存在弱相关性。

鉴于近岸区域波浪的生态意义极为重要，定量分析涌浪的比例有利于提高计算波浪切应力的精度。 从 H  sw /H w 随风向的变化来看（见图10），绝大部分  H  sw /H w  的样本均大于0.6。从其随风向分布来看，偏东风的风区较短，风直接驱动产生的波浪很弱，因而波浪中涌浪占比接近于1。为此，在评价近岸区波浪的动力过程中，应在风浪上叠加基于耦合风速估算的涌浪成分，提高估算波浪切应力的精度。

3 讨 论

太湖属于典型的大型浅水湖泊，平均水深仅有 1.8  m。其谱峰频率（0.5 Hz）远大于海洋的谱峰频率（ 0.075  Hz）;波峰最大能量（0.001 m  2 /Hz）远小于海洋的对应值（2.5 m  2 /Hz）  [13] 。在太湖北部开阔区域的波高随风速遵循e指数函数的形式，与本文中风向对有效波高的影响特征相吻合，但其参数受周边地形等因素的影响显著  [8] 。与海洋相比，太湖水浅，加之面积不大，使得湖泊水体从风场中获取的能量较少，因而其波能远小于海洋。也正是因为水浅，使得波浪引发的切应力可作用于湖底，成为导致底泥再悬浮、影响水生生态系统的关键因素。

太湖属于典型的内陆湖泊，风速和风向的耦合与综合波浪有效波高的关系证实了风速（尤其是耦合风速）是太湖的主要驱动力。内陆湖泊风向变化显著，风区长度的空间变化明显，使得风速、风向对波浪的驱动作用空间差异明显，其中风向通过三角函数的形式调制风速对波浪起驱动作用。加上沿岸对波浪的反射等特征，导致波浪组成比例时空差异突出，因而近岸区的波浪特征远比开阔区复杂，且呈现出显著的空间差异特征。

本文所用数据的观测时段超过13 d，期间经历了完整的台风（苏力）影响过程，其风速变化范围宽泛（见图2（b））;风向的变化也涵盖了0～2π的范围（见图4），可见观测到的波浪数据既体现了风场（风速、风向）的驱动效应，也包含了岸界的反射信息，甚至也反映了风场与岸界的耦合效应。因而，本文的数据涵盖了风场和波浪的多个过程及其演变规律（见图2（a）及图3），具有良好的代表性。

近岸区对波浪的反射作用会改变波浪的组成，提高涌浪的比例。这种改变效应也受风向及岸界的共同影响，因而近岸区的波浪中含涌浪比例很高，其比例最低大于0.6，最高大于0.9。由于在大型浅水湖泊中波浪对耦合风速响应迅速，加上近岸岸界反射作用使得涌浪在一定程度上携带了耦合风速的信息，因而太湖中波浪与耦合风速的关系较海洋中更为密切;但又和海洋一样，波浪中包含了较高比例的涌浪，因而本次研究的进展将提高近岸区波浪参数化方案的精度。

4 结 论

（1） 太湖北部近岸区波浪呈现中高频特征，三角函数可以表征风向对波浪的定量影响。

（2） 风速（尤其是耦合风速）是太湖波浪的主要驱动因素，该区波浪既包含风浪，也包含涌浪，其中涌浪的占比较高，且随风向变化。

（3） 太湖北部近岸区的涌浪随耦合风速呈现快速和缓慢的e指数增长现象。

致 谢

感谢中国科学院太湖生态系统实验站为本次研究提供相关的气象数据。

参考文献：

[1]  GARCIA  G W.Wave bimodal spectrum based on swell and wind-sea components[J].IFAC-Papers OnLine，2015，48-16：223-228.

[2] HANSON J L，PHILLIPS O M.Automated analysis of ocean surface directional wave spectra[J].Journal of Atmospheric and Oceanic Technology，2009，18：277-293.

[3] DING W，WU T，QIN B，et al.Features and impacts of currents and waves on sediment resuspension in a large shallow in china[J].Environmental Science and Pollution Research，2018，25：36341-36354.

[4] 罗敛葱，秦伯强.太湖波浪与湖流对沉积物再悬浮不同影响的研究[J].水文，2003，23（6）：1-4.

[5] 文圣常，余宙文.海浪理论与计算原理[M].北京：科学出版社，1984.

[6] 逄勇，庄巍，韩涛，等.风浪扰动下的太湖悬浮物实验与模拟[J].环境科学，2008，29（10）：2743-2748.

[7] 朱广伟，许海，朱梦圆，等.三十年来长江中下游湖泊富营养化状况变迁及其影响因素[J].湖泊科学，2019，31（6）：1510-1524.

[8] 胡维平，胡春华，张发兵，等.太湖北部风浪波高计算模式观测分析[J].湖泊科学，2005，17（1）：41-46.

[9] 范成新，刘元波，陈荷生.太湖底泥蓄积量估算及分布特征探讨[J].上海环境科学，2000，19（2）：72-75.

[10]  许遐祯，陶蓉茵，趙巧华，等.大型浅水湖泊太湖波浪特征及其对风场的敏感性分析[J].湖泊科学，2013，25（1）：55-64.

[11] BISSINGER J E，MONTAGNES D J S，SHARPLES J，et al.Predicting marine phytoplankton maximum growth rates from temperature：Improving on the Eppley curve using quantile regression[J].Limnol.Oceanogr.，2008，53（2）：487-493.

[12] PORTILLA J，MONBALIU J.Spectral partitioning and identification of wind sea and swell[J].Journal of Atmospheric and Oceanic Technology，2009，26：107-122.

[13] KPOGO-NUWOKLO KA，AILLIOT P，OLAGNON M，et al.Improvement ocean wave spectra estimation using the temporal structure of wave systems[J].Coastal Engineering，2015，96：81-91.

（编辑：胡旭东）

Analysis on wave composition and evolution characteristics in northern coastal  area of Taihu Lake in summer

ZHAO Qiaohua，XU Jia，WANG Jianjian

（ School of Hydrology and Water Resources，Nanjing University of Information Science and Technology，Nanjing 210044，China ）

Abstract：

Wave is the key dynamic process that drives the evolution of aquatic ecosystem in large shallow lakes.In this paper，the wave composition and its evolution characteristics were analyzed based on the observation data of wave direction spectrum，wind speed and wind direction in the northern coastal area of Taihu Lake.The results showed that the wave frequency spectrum in the near-shore area of northern Taihu Lake was mainly unimodal or bimodal，belonging to medium and high frequency wave.Wind is the main driving force for wave formation，and the modulation of wind direction or surrounding terrain on the significant wave height can be quantitatively characterized by trigonometric function.The relationship between the significant wave height，spectral peak frequency and its average direction of wind waves，and wind speed or direction confirmed that the wave in the northern coastal area of Taihu Lake were composed of surge and wind waves，and the surge proportion was relatively high.The reflection of the shoreline increased the surge proportion in the northern coastal area.The significant wave height of surge not only increased exponentially with the coupling wind speed （coupling of wind speed and wind direction），but also had the phenomenon of fast and slow differentiation.The research results can help to improve the accuracy of wave composition estimation in the near-shore area of large shallow lakes，and ensure the effect of aquatic ecological restoration.

Key words：

wave composition;wind wave;surge;significant wave height;Taihu Lake