基于EOF 迭代的自动气象站气温观测资料修复方法
2022-04-15沈王彬李昕秦正坤张冰
沈王彬 李昕 秦正坤 张冰
1 南京信息工程大学大气科学学院,南京 210044
2 南京信息工程大学资料同化研究与应用联合中心,南京 210044
3 南京气象科技创新研究院/江苏省气象科学研究所,南京 210009
1 引言
大气边界层是下垫面与自由大气进行物质与能量交换的重要场所,在大气边界层中时刻进行着诸如湍流动量和热量交换等过程,一些常见的天气现象如雾和降水以及一些爆发性气象灾害如暴雨和沙尘暴与边界层中的物理过程有密切联系。地表热力通量和水汽通量通过边界层上传自由大气,影响天气过程演变。因此,地面观测资料在天气预报预警中具有重要作用。
随着观测技术的发展,目前我国已经建立了巨大且密集的地面气象观测网络,全国已建成约七万个自动气象观测站,自动气象观测站能够定时、定点的观测和记录地面气象信息,并且能够在复杂的地形下进行无人观测(张慧, 2012)。但是自动化气象观测事业的发展同时也带来了些许问题,张颖超等(2017)、徐浩然(2019)指出随着观测自动化的实现,原有的业务模式发生改变,但是地面观测技术的不稳定导致地面观测资料更容易出现质量问题,一方面众多台站的观测资料往往由于采集、传输或仪器自身的系统问题,不可能达到完全正确无误,另一方面,区域自动站资料的质量控制和评估工作较为滞后,直接影响了资料在预报预测业务中的使用。
为了提高区域自动气象站观测的数据质量,需要通过质量控制来保证数据质量(Lorenc and Hammon, 1988)。近十年来,我国气象工作者在实时观测资料自动质量控制方面做了大量的研究工作。国内外有关地面气象资料的常规质量控制方法主要有气候学界限值检查、台站或区域极值检查、要素间内部一致性检查、时间一致性检查以及空间一致性检查等方法。王海军等(2007)、陶士伟等(2009)、陈兴旺(2011)、赵煜飞等(2011)都利用常规质量控制方法对我国的地面观测资料进行了质量控制试验。李良富等(2006)和叶小岭等(2016)还尝试了利用人工智能的黑板模型和基因表达式编程方法进行了质量控制。基于空间分析方法EOF(Empirical Orthogonal Function)分解方法,Qin et al.(2010)和邵宇行等(2021)针对全国高时间和空间分辨率的地面自动站观测资料,对前人提出的基于EOF 分析的质量控制方法进行适应性的调整,并利用我国中东部的自动站观测资料进行实际质量控制试验,发现该方法可以很好适用于高时空分辨率的地面自动站观测资料。
错误的自动站观测资料会对天气预报和气候变化研究带来严重的影响,根据研究目的不同,气象学家对错误资料的处理方法也不尽相同。气候研究往往是对资料的稳定性提出较高的要求,如何把误差的大小控制在气象业务所允许的范围内,提供一个在时间和空间上更加完整的观测资料数据集,以确保历史观测资料的连续性是自动站观测资料应用上面临的问题(王晓春等,1994;江志红等,2008;曹丽娟和严中伟, 2011)。而在资料同化应用中,为了保证同化增量的合理性,往往倾向于直接剔除可疑的观测资料(薛纪善, 2009),但错误资料也并非完全不可利用,在进行有效订正的前提下,通过对订正后资料进行合理的、定量化的观测误差调整,将使得这些资料在模式中的应用变为可能。
资料序列的订正方法研究是国内外学者所共同关注的问题之一,并已有不少研究。根据方法的原理不同,目前的错误资料或者缺测资料的修复方法大致可以分为以下三类:一是利用观测资料本身的规律或者不同气象变量之间的物理关系来进行资料修复,多用于气候资料(Annan and Hargreaves,2013; 李天祺等, 2015; 周芳成等, 2021),或者规律性 显 著 的 资 料(Göttsche and Olesen et al., 2001;Duan et al., 2012);二是利用随机模型方法,利用扰动的随机样本之间的相似性来修复数据,比如神经网络方法(Wu et al., 2019)、自组织映射法和期 望 最 大 化 法 等(Sorjamaa and Lendasse, 2007;Zhao et al., 2020);三是根据变量的时空特征,利用最优化和多维统计方法来修复资料,比如最优插值方法(朱江等, 1995; Everson et al., 1997)、经验正交函数(EOF)分解方法(Alvera-Azcárate et al.,2009; 盛峥等, 2009; Shen et al., 2019)。
同时,研究也发现没有绝对最优的空间内插方法,必须对所研究的数据进行空间探索分析,根据数据的特点,选择相应方法,对某一种气象要素合适的插值方法未必对另一种气象要素合适(蔡彦枫等, 2015)。我国目前已经建成了近七万个地面自动观测站,高时空分辨率的地面自动站资料最大的特征就是小尺度特征强,时空变率大,容易出现极值情况,尤其是对于天气变化尺度的研究,仅依赖于温度的日变化等变量固有的规律性特征进行修复容易出现较大的误差,而较多的极值情况也导致了基于随机性的修复方法存在一定的不足,所以依赖于周边资料来修复地面站温度资料是一种比较可行的方法。
最优化和多维分析方法都可以依据周边资料来修复单个错误资料,但是最优化方法往往需要资料的误差等先验信息,所以基于EOF 等多维分析方法的错误资料修复方法就成为更为简单易行的方法。基于EOF 分析的时空分离的特征,Alvera-Azcárate et al.(2009)和Shen et al.(2019)都提出了基于EOF 空间分析方法的错误资料修复方法。EOF 方法的优点在于利用空间降维技术将原始变量场的时空结构进行正交分解,得到为数很少的不相关典型模态来代替原始变量场。EOF 方法提取的典型模态存在两个重要特征,一是模态是在考虑了变量场时间和空间变化特征后确定的,不容易受到少数极值资料的影响,这种特征对于提取小尺度信号强的地表信息时尤为重要;二是EOF 方法提取的各个模态是相互正交的,各个模态及其对应的系数在处理过程中不会相互影响,所以可以考虑通过迭代的方法逐步确定各个模态的系数,不需要考虑不同模态系数之间的相互影响。利用EOF 分析方法的这两个特征,我们就可以建立一个基于迭代的错误资料修复方法。首先利用EOF 分析方法将研究区域的大气温度分离为不同尺度的空间模态,然后分别针对代表不同时空尺度的EOF 模态,通过迭代的方法消除错误资料对EOF 分析模态的影响。由于个别错误资料不会影响各个模态所对应的时间系数,结合迭代修正的EOF 分析模态和稳定的时间系数,我们就可以具有很好的时空连续性的修复结果。
本文将针对全国自动气象站观测资料高时空分辨率的特征,在有效识别自动气象站异常观测资料的基础上,利用EOF 分析方法,建立一个新的基于EOF 迭代方法的错误资料修复方法,并对中国东部自动站气温观测资料进行了错误观测资料的修复试验,希望为自动气象站错误观测数据的修复提供科学依据。
2 资料和方法
2.1 数据说明
本文选取的资料为江苏省气象局通过全国综合气象信息共享平台CIMISS(China Integrated Meteorological Information Service System)数据库实时接收的2019 年12 月1 日00:00 至7 日23:00(北京时,下同)的逐小时地面自动站观测资料,共168 个时次的地面观测站温度观测资料。选取的研究区域为(29°N~39°N,113°E~123°E)。高水平分辨率是自动站观测资料的主要特点,图1 给出了自动站站点的空间分布特征,其中站点分布最密的主要是在江苏、山东和安徽三个省份。

图1 地面自动观测站点(黑色点)水平空间分布Fig.1 Spatial distribution of ground automatic observation stations(black points)
由于观测资料中存在大量缺测资料,为了保证研究结果的普遍性,我们需要对某些时刻缺测值进行时间三次样条插值,但是由于某些站缺测时刻过多导致时间插值后存在极端异常值。所以为了尽可能的消除时间插值对检测结果的影响,我们首先对观测资料进行筛选;筛选的条件有:(1)前五个时次无缺测,(2)后五个时刻无缺测以及(3)168 个时次至少有1/10 资料无缺测;最终该区域包含4983 个观测站。
2.2 质量控制方法
对自动气象站气温观测资料进行质量控制,准确的识别出其中错误的资料是修复错误资料的前提。为此,邵宇行等人(2021)提出了基于EOF 的高时空分辨率自动站温度观测资料质量控制方法。按照该方法首先利用传统质量控制方法对资料进行了预处理,去除了数据中明显存在的误差。在此基础上,以ECWMF(European Center for Medium-Range Weather Forecasts)的ERA5 2 m 温度再分析资料作为背景场信息,使用EOF 质量控制方法对筛选出的4983 个站点进行了质量控制。
图2 给出了基于该质量控制方法识别出的168个时次的错误资料个数曲线。平均剔除资料为每日48 个,剔除率约为0.96%,大部分时间错误资料量都是稳定在50 个左右,只是在第136 时次和第146 时次错误资料个数异常偏多。

图2 2019 年12 月1~7 日质量控制方法剔除资料量的时间变化曲线Fig.2 Hourly data count of abnormal data detected by the quality control method during December 1–7, 2019
为了明确剔除资料的正确性,图3 给出了2019 年12 月1 日11:00 四个离群观测站点及其周围站点的气温分布情况,黑色阴影表示地形高度。该时次一共识别出89 个离群站点,主要分布在安徽省的中部及南部。根据四个错误站点以及周围站点的温度分布可以看出,错误站点在第36 个时次相较于周围站点观测温度均为异常高值,因此可以认定基于EOF 的质量控制方法识别的错误资料是合理的。虽然质量控制方法能够剔除绝大部分温度异常的站点,但是依然可能存在漏检现象,图3 中的区域中部(30.72°N,116.45°E)可以看到存在一个明显低于周边站点温度的资料,这可能还需要更长时间的资料来评估研究区域地面温度的空间连续性特征,后续研究中我们将引入更长时间资料来完善目前的质量控制方法。

图3 2019 年12 月1 日11:00(第36 时 次)局部温度数 值(单位:°C)。图中阴影表示地形高度(单位:m),红色为剔除站点Fig.3 Spatial distribution of the observed temperature (units: °C) at 1100 BJT (Beijing time) December 1, 2019 (36th hour). The shading indicates the terrain (units: m) and the red dots represent the abnormal stations
从错误站点的识别结果可以看出,自动站观测资料在每个时刻均存在50 个左右的错误资料,在数值天气预报需求日益精细化的背景下,错误资料会对天气预报带来很多消极的影响。因此,在对错误站点进行准确识别的基础上,本研究的主要的目的是对错误气温资料进行准确的修复。
2.3 地面自动站错误资料修复方法
在利用前期质量控制方法有效识别错误的气温观测资料基础上,我们将尝试对错误资料进行修复研究。为了不失一般性,我们将尝试修复其中任选的一个错误观测站s的气温观测资料。
高时空分辨率的地面自动站温度观测资料也具有时空变率强的特点,所以基于变量规律性特征或相似样本的修复方法存在一定的不足,因此利用周边观测信息修复某个站点的错误资料最为可行。基于最优插值方法和基于多维分析方法的修复方法是最常用的基于周边观测信息修复单个观测资料的方法。这里我们分别选用了两类修复方法,一是基于Cressman 空间插值方法的修复方法,二是利用Shen et al.(2019)建立的基于EOF 分析方法的迭代修复方法。
2.3.1 基于Cressman 空间插值修复方法
Cressman 插值方法是一种比较经典的非规则格点空间插值方法(Cressman, 1959),该方法的基本原理是基于相邻越近的站点在空间分布上具有越相近特征的假设,由于地面自动站高空间分辨率的特点,因此利用错误站点周围正确的气温观测资料,通过空间插值方法可以获得该点的观测信息。该方法的基本形式如下:

其中,fi是第i个需要被修复的观测站点的气温值,W(Di)是Cressman 权重系数,其形式为

式中,R为影响半径,这里经验的设定为0.75°,Di为错误站点与周围正确观测站点的距离。由权重函数可以看出,距离被修复的点越近的点权重函数越大,符合Cressman 插值基本原理。
2.3.2 基于EOF 迭代修复方法
基于EOF 的迭代修复方法首先是建立用于EOF 分析的数据矩阵。假定地面站s点被检测为错误观测站,再选取空间内所有观测站的观测资料,剔除其中已经检测的所有错误气温观测资料,剩余观测站数记为n。考虑到地面温度的日变化,对于已选的n个观测点,选择每个观测点上当日连续24 个时次的逐小时观测数据,假定修复某观测站第12 时次的气温观测资料,那么这里的24 个时次选为:当日00:00~23:00 连续24 个时次的观测气温,记为Ti, j,其中i=1,2,···,24 表示一共选取24个时次的观测资料,j=n表示一共选取n个站点进行重构。
最终用于修复的数据矩阵可以表示为Am×n:

其中,m=24,代表所选的24 个时次,假设其中第x个时次,第s观测点Tx,s为错误资料,也是用于重构的观测点。为了增强错误资料与其周边资料点之间的小尺度异常特征,可以设Tx,s=0。对上述矩阵A进行EOF 分解,我们可以得到:

式中,Vk一般称为模态向量,而Zk则是系数向量,k代表第k个模态,因为所选的观测站数肯定是大于时次数,所以EOF 分析获得的模态数最多为m个。
由于EOF 第一模态提取的是资料的平均特征,所以有理由认为第一模态不会包含异常点0 值的信息,那么利用第一模态进行重构就可以得到:
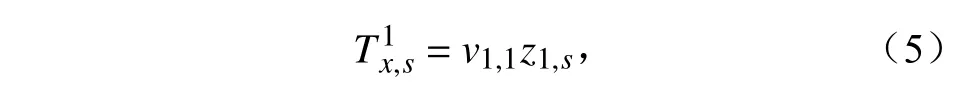
获得准确的第一模态信息是保证方法修复效果的前提条件。虽然0 值的异常信息不会被包含到第一模态中,但是0 值仍然可能使得应有的第一模态信息被分散到其他模态中。因此需要通过迭代的方式逐步完善第一模态所代表的平均特征。
在获得Tx1,s后,我们将该值带入到原来的数据矩阵,组成新的数据矩阵A1,即:

对矩阵A1再次进行EOF 分解可得:

同样获得基于第一模态重构获得的s点气温,即:
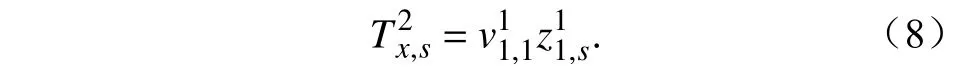



图4 2019年12月4日00:00~23:00(a)用来重构的气温分布(单位:°C)以及(b)随迭代次数的变化曲线Fig.4 (a) Spatial distribution of temperature (units: °C) for reconstruction and (b) variation of with the number of iterations for station s from 0000 BJT to 2300 BJT on December 4,2019
实现了第x个时次s点气温第一模态特征完全再现的基础上,我们继续提取第二模态的信息。经过t1次迭代后,构造的新的数据矩阵为At1为

对矩阵At1进行EOF 分解,并利用前两个模态重构s点地面温度:
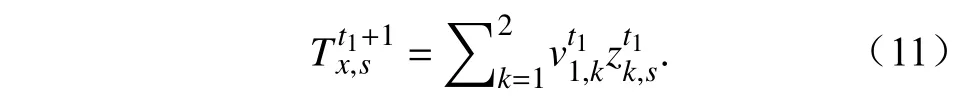
从前面的分析可以知道,我们已经获得了Tx,s稳定的第一模态信息,并构造了新的数据矩阵,这等同于将除第1 模态外的其他模态分量设为0,简单的重复上述迭代过程,我们可以获得具有前两个模态准确信息的T。同样通过对更多模态进行上述迭代过程,我们可以依据EOF 提供的周边观测点信息和其它未受干扰的通道观测信息的约束条件下,获取包含尽可能多正确观测信息。
理论上可以对所有模态进行提取,所以图5 也给出了不同模态迭代过程中误差的变化曲线,图中不同颜色分别代表不同的模态。可以看到,前七个主要模态迭代结束后,重构值趋于稳定,此时误差在0.5°C 左右。继续对剩余的模态进行提取,可以

图5 重构过程中观测值与重构值的差随迭代次数的变化曲线(单位:°C)。不同颜色分别代表不同的模态Fig.5 Temperature differences between the observed and the reconstructed temperature varying with the number of iterations (units: °C). Different colors represent different modes
看到,由于剩余模态包含一些小尺度的气温场信息,因此重构误差曲线出现了一些波动,但是当所有模态均被提取后,重构误差小于0.1°C。
3 结果与分析
3.1 重构方法精度分析
在新的修复方法适用之前,应该对该方法的修复精度进行评估。首先选取单个时刻的气温观测资料中的正确资料作为验证数据。图6 给出了2019年12 月4 日14:00(第87 个时次)用EOF 质量控制方法识别出的错误站点的分布。可以看到,该时次一共出现19 个错误站点。

图6 2019 年12 月4 日14:00(第87 个时次)EOF 质量控制方法识别出的错误站点(红色圆点)分布Fig.6 Spatial distribution of abnormal data (red points) at 1400 BJT December 4, 2019 (87th hour)
对该时刻所有正确资料逐个进行重构,将重构结果与观测进行对比,并统计其均方根误差可以有效的验证重构方法的精度。均方根误差的计算公式如下:
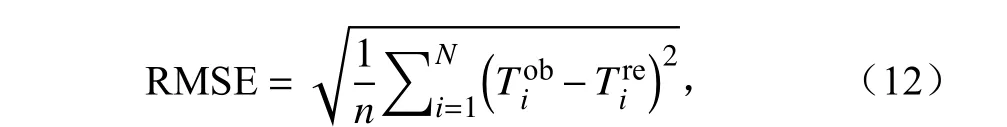
其中,n表示选取的站点数,T为站点的观测气?温值,T为重构得到的站点气温。若均方根误差越小,则表明重构结果精度更高。
图7 给出了2019 年12 月4 日14:00(第87 个时次)正确观测气温、两种方法重构的气温分布以及观测与重构的误差(观测减去重构)。从自动站正确观测资料的分布可以看到,自动站空间分辨率较高,因此能很好分辨更多小尺度的温度变化特征。空间分布形态也是评价插值方法的重要方面,对比基于EOF 迭代法和Cressman 插值法得到的气温分布,可以看到,EOF 迭代法重构的气温与观测非常接近,重构场不仅能准确的描述气温观测的空间特征,对于观测中存在的一些极值也能很好的还原,这是由于EOF 方法考虑了变量场时间和空间变化特征,不容易受到少数极值资料的干扰,也不易受观测站点分布的疏密程度和不均匀性的影响。而Cressman 插值法得到的重构场只能大致反映观测气温的特征,但是在极值和极值附近区域重构值与观测存在较大差异,原因是Cressman 方法只考虑周围站点的距离来确定其权重, 而不考虑它们之间的空间相关性,即是站点距离越近则变量值越大,分析值就越靠近,从而在极值及其附近区域出现偏向的特征。统计结果表明EOF 迭代法的重构均方根误差为0.41°C,而Cressman 插值的重构均方根误差为1.25°C,远大于EOF 迭代法,从重构误差的分布上可以看到,EOF 迭代法的重构误差基本在0.5°C 以内,并且误差的分布比较随机,与气温本身高低无关。Cressman 插值重构的误差较高,尤其在地形变化强烈的区域附近,如安徽省的大别山以及黄山附近。由于地形影响,气温在大地形附近出现了较大温度梯度,但是Cressman 插值仅考虑测站之间的距离,不能结合观测站之间的空间相关性,因此插值结果误差较大。

图7 2019 年12 月4 日14:00(第87 个时次)观测气温、重构气温以及误差(观测减去重构)的分布(单位:°C):(a)观测气温;(b)EOF 迭代法重构气温;(c)EOF 迭代法重构气温的误差;(d)Cressman 插值法重构得到的气温;(e) Cressman 插值法重构气温的误差Fig.7 Spatial distributions (units: °C) of observed and restored temperature and their difference distribution at 1400 BJT December 4, 2019 (87th hour): (a) Observed temperature; (b) restored temperature of EOF method; (c) restoration error of EOF method; (d) reconstructed temperature of Cressman interpolation method; (e) reconstruction error of Cressman interpolation method
为了增大样本数来提高统计可信度,我们又选择了2019 年12 月1~7 日 共168 个时次,共计808260 个正确的气温观测,分别使用EOF 迭代法和Cressman 插值法进行重构。经统计,EOF 迭代法和的重构均方根误差分别为0.48°C 和1.55°C,Cressman 插值的误差远大于EOF 迭代法,这与图7的结论一致。图8 给出了所有正确观测气温与重构气温的散点图,黑色点表示EOF 迭代法对应的散点,灰色点表示Cressman 插值法对应的散点。可以明确看到,EOF 迭代法重构的气温与观测值较为接近,重构误差较小,而Cressman 插值法由于受多方面的干扰重构效果较差,重构后的气温表现出来的特征不明显,其误差明显大于EOF 迭代法。

图8 观测气温与EOF 迭代法(黑色点)以及Cressman 插值法重构气温(灰色点)散点图(单位:°C)Fig.8 Scatter plots between the observed and reconstructed temperature of the EOF iteration method (black spots) and the Cressman interpolation method (gray spots), units: °C
进一步分析重构误差的分布情况,图9 给出的是观测值与重构值误差的概率密度函数分布曲线。可以看到,EOF 迭代法重构误差分布的峰度系数为210,误差绝对值基本集中在0.5°C 以内,只有极少数误差绝对值大于1°C,但是极值也在2°C 以内。而Cressman 插值重构误差峰度系数为83.67,很大一部分站点的重构误差大于1°C。因此,相对于Cressman 插值而言,EOF 迭代法具有更高的稳定性和更高的精度。
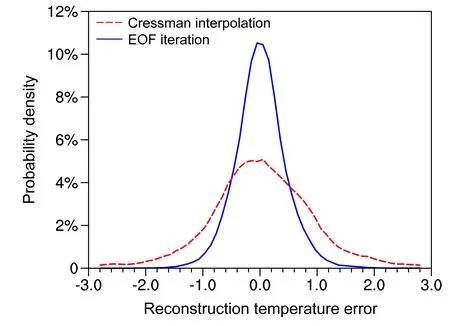
图9 EOF 迭代法(蓝色实线)以及Cressman 插值(红色虚线)的重构误差概率密度曲线(单位:°C)Fig.9 The probability density function of the reconstruction error for the EOF iteration method (blue solid line) and the Cressman interpolation method (red dotted line) during 1–7 December 2019(units: °C)
3.2 实际重构结果分析
在根据正确数据对EOF 迭代法的修复精度进行理想评估后,我们将修复方法应用到实际错误资料的修复中进行检验。分别使用EOF 迭代法和Cressman 插值法对基于EOF 的自动站质量控制方法识别出的错误站点进行修复。图10a 给出了2019 年12 月4 日14:00(第87 个时次)局部温度数值(红色为错误站点温度数值),图中的阴影表示地形高度。两个站点在第87 时次被判定为离群点,根据两个站点第87 时次的温度及其周围站点温度分布可以看出,两个站点在第87 时次相对于周围站点温度为异常高值,并且该错误站点的地面温度观测并未受地形的影响,因此可以认定质量控制方法判定的错误资料是合理的。使用两种方法对该错误站点进行重构,图10b、c 分别给出了基于EOF 迭代法和Cressman 插值法修复的地面气温,可以看到,EOF 迭代法重构的气温值明显低于错误的观测气温,并且修复值与周围观测值更加接近,而Cressman 插值结果与周围观测相比则异常偏低,这是由于错误站点南部出现了地形高度增加的情况,随着地形高度的增加地面温度也出现了明显的降低,因此区域南部气温普遍低于区域北部,由于Cressman 插值只考虑测站空间距离因素,南部的低温资料会使得最终插值结果偏低。EOF 迭代法则能综合考虑气温的空间典型分布特征,使得重构结果不受地形影响。因此,EOF 迭代法修复后的气温分布连续性更佳,其平滑性和规律性更好,修复效果也更好。
重构的气温分布已经验证了修复气温在空间分布上的合理性。另一方面,自动气象站逐小时高分辨率的气温观测资料为精细化研究气温的日变化差异、季节及气候特征带来了可能性,因此,修复后的气温随时间变化是否合理也是评估修复气温质量的一项重要指标。图11 给出了图10 中两个识别出的错误站点的观测以及修复后气温的日变化曲线,可以看到,与周围站观测气温相比,两个存在错误观测资料的站点均在第15 时次出现了异常偏高的观测气温(红色线),在该时刻远高于周围所有观测站的气温(灰色线)。对北部站点而言,经过EOF 迭代法修复后(蓝色线),错误站点气温的时间变化趋势与周围站点基本一致,符合气温日变化的规律,而Cressman 插值得到的气温(黑色线)在该时刻出现异常偏低的不合理变化趋势。这是由于EOF 迭代法不仅能考虑到气温的典型空间分布特征,同时其在气温的时间变化趋势约束下对错误观测进行重构,最终得到的重构结果能同时满足气温的时空特征,而Cressman 插值结果则受到观测站南部地形影响,插值结果异常偏低。

图10 2019 年12 月4 日14:00(第87 个时次)(a)局部观测气温、(b)EOF 迭代法重构气温以及(c)Cressman 插值气温分布,单位:°C。图中黑色阴影表示地形高度(单位:m)Fig.10 Spatial distribution of (a) observed temperature, (b) restored temperature by the EOF iteration method and (c) restored temperature by the Cressman interpolation method at 1400 BJT on December 4, 2019 (87th hour), units: °C. The shading indicates the terrain (units: m)

图11 2019 年12 月4 日10:00~20:00 观测气温(红色)、重构后气温(蓝色)、Cressman 插值后(黑色)气温以及周围站点的气温(灰色)序列(单位:°C)Fig.11 Time series of (a) observed temperature and (b) restored temperature by the EOF iteration method and (c) restored temperature by the Cressman interpolation method during 1000 BJT–2000 BJT on December 4, 2019 (units: °C)
4 结论与讨论
错误的自动站观测资料对天气预报和气候变化研究带来很大的限制,地面气候研究以及各个领域需要的专业气象服务往往需要完整的自动站观测数据,因此对异常观测的资料序列进行订正,确保观测资料的准确性和连续性至关重要。
本文利用江苏省气象局提供的2019 年12 月1日00:00 至7 日23:00,共168 个时次的地面自动站温度观测资料,在EOF 的质量控制方法有效识别异常观测资料的基础上,提出一种新的基于EOF 的迭代方法用于修复错误的自动气象站地面气温观测。
结果表明,利用本文提出的EOF 迭代修复法可以较高精度的对地面气温观测进行重构,其重构均方根误差为0.48°C,远小于Crssman 插值法,并且EOF 迭代法修复后的气温在时空特征上都具有合理性。这是因为EOF 迭代法不仅考虑了地面气温的典型空间分布,还利用了气温随时间变化的特征对重构进行约束,从而从整体上考虑了插补资料的效果。而Cressman 一类的插值方法只选取了错误点周边的部分资料,通过资料的连续性进行插值,但是其插值过程中不能考虑其他周边资料的约束,所以容易受到个别极端资料的影响,这对于小尺度信息较强的地表变量来说,更容易出现不稳定现象。
由于资料长度的限制,本文没有对长时间的气温观测进行修复试验,在后续的研究中我们将针对更长时间的观测资料进行重构检验。另一方面,目前的工作只针对地面气温展开,在以后研究工作中还应考虑利用EOF 迭代法对其他一些地面观测变量进行修复,例如相对湿度、降水等。
