Data Recovery from Cauchy Measurements in Transient Heat Transfer
2022-04-15ThourayaBarangerNouriandFakerBenBelgacem
Thouraya Baranger Nouriand Faker Ben Belgacem
1Universit´e de Lyon,Universit´e Lyon 1,LMC2,EA 7427,F69622 Villeurbanne Cedex,France.
2Universit´e de Technologie de Compi`egne,LMAC,EA 2222,BP 20529,60205 Compi`egne cedex,France.
Abstract.We study the ill-posedness degree of the reconstruction processes of missing boundary data or initial states in the transient heat conduction.Both problems are severely ill-posed.This is a powerful indicator about the way the instabilities will affect the computations in the numerical recovery methods.We provide rigorous proofs of this result where the conductivites are space dependent.The theoretical work is concerned with the unsteady heat equation in one dimension even though most of the results obtained here are readily extended to higher dimensions.
Key words:Data completion process,ill-posedness degree,Cauchy matrix,convolution equations,parabolic regularity.
1 Introduction
Computational recovery processes of missing boundary data or initial states from Cauchy measurements in transient heat transfer seem recurrent in many areas in sciences and engineering(see[5,6,23]).They turn out to be among few pertinent ways to proceed,if not the only one,when engineers are interested for example in quantifying front surface heat inputs of a(thin)plate from back surface outputs.Mounting measurements setup along the front surface may not be feasible due to harsh environmental conditions.Practitioners are therefore led to place sensors at the back surface;they are then left with the evaluation,by means of affordable(analytical and/or numerical)tools,of the heat transfer up to the front surface.The particularity of the related mathematical problem is the ill-posedness.Missing data to reconstruct suffer from high instabilities generated by unavoidable perturbations affecting the available data because of the finite accuracy of measuring instruments(see[2,3,14,17,18,22,31,32]).As a consequence,computing methods crudely employed for numerical handling of these inverse problems are most often doomed to fail unless they are used with relevant regularization techniques combined to suitable automatic selection rules of the regularization parameter(s).Readers are referred to[4,15,19,24,25,33]for a general exposition of these issues.We are exclusively focused on the issue of ill-posedness degree for the reconstruction problem of either the initial or the boundary data from Cauchy’s measurements.The purpose is then to perform a rigorous analysis on the severe ill-posed of the inverse problems under scope.We develop in details methodologies for the transient heat equation set in a rod.This choice is made only for seek of simplicity.We do not see why the central ideas discussed here cannot be effective for higher dimensions.
The contents of the paper are as follows.Section 2 is dedicated to the study of the initial state recovery from Cauchy’s conditions.After defining the linear operator to invert,we study some of its marked features.Expanding this operator along Fourier basis shows that the ill-posedness degree is connected with a Cauchy matrix.This matrix is spectrally equivalent to a Pick matrix.Using the theory elaborated in[7],we exhibit the asymptotics of its eigenvalues.They decay exponentially fast towards zero which is an indication of the severe ill-posedness of the reconstruction process of the initial state.In Section 3,we turn to the recovery of a missing boundary condition at one extremity of the rod,where the initial state is known.We follow a similar approach,we define the linear operator to analyze and underline its distinctive properties.The key point is to put it under an integral form using a suitable Green kernel.The smoothness and the flatness at the origin of that kernel is the clue to the analysis of the ill-posedness degree.It is derived in the appendix thanks to the Laplace transform and some comparison results.In Section 4,we provide two numerical illustrations by MATLAB of the technical results stated in the previous sections.
Notation 1.1.LetXbe a Banach space endowed with its norm ‖·‖X.We denote byL2(0,T;X)the space of measurable functionsvfrom(0,T)inXsuch that
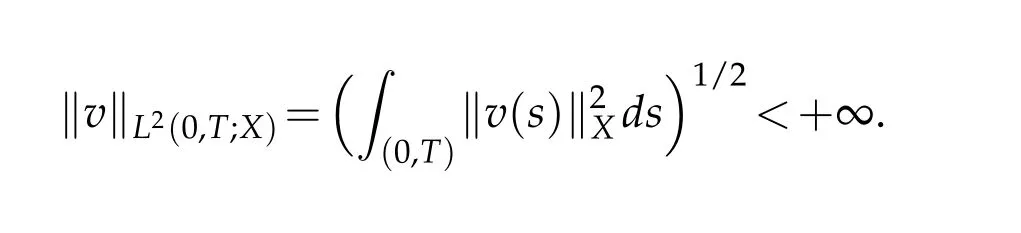
We also use the space C(0,T;X)of continuous functionsvfrom[0,T]inX.Denote byIa given interval in R,the Sobolev spaceH1(I)is the space all the functions that belong toL2(I)together with their first derivatives.
2 Initial condition reconstruction
Let a rod be geometrically represented by the segmentI=(0,π)andT>0 be a fixed realnumber.We setQ=I×]0,T[.The generic point inIis denoted byxand the generic time ist.Assume now be givenψinL2(I)and denote byyψthe unique solution of the heat problem

The symbol′is used for the space derivative∂x.The conductivity parameterγ(·)∈L∞(I)is piecewise continuously differentiable and is supposed to be positive and bounded away from zero.This means thatγm=minx∈Iγ(x)>0.We also setγ∞=maxx∈Iγ(x)=‖γ‖L∞(I).The functionyψexists and lies inL2(0,T;V)∩C([0,T];L2(I))(see[26,Chap.4]),where the spaceVis set to be
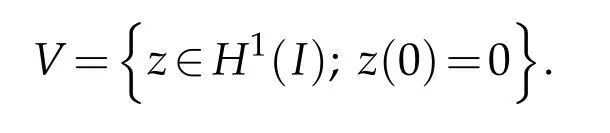
The inverse problem to deal with here is the reconstruction of the initial conditionψfrom an additional boundary data atx=π,related to abundant observations at that extreme-point.Hence,for a given functionh=h(t)∈L2(0,T),we intend to findψ∈L2(I)satisfying the following Dirichlet condition
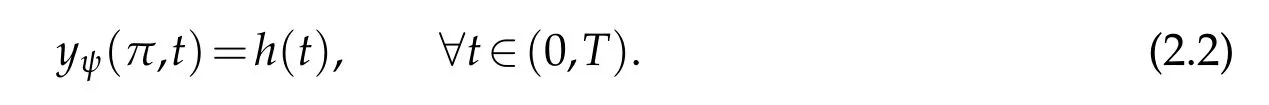
The point we focus on is the ill-posedness degree of this observation problem,an indication of how unstable it is.We refer to[36]for the general introduction of this notion and to[34](see also[24,35])for a definition specifically adapted to the problems under investigation.
2.1 Uniqueness and admissible data
That problem(2.2)is ill-posed is widely known.No existence is guaranteed and the hypothetical solutionψ(·)does not depend continuously on the datah(·).The identifiability is the only result one may obtain.Indeed,we have
Lemma 2.1.The inverse problem(2.2)has at most one solution.
The methodology followed in the subsequent consists in the investigation of the linear operator
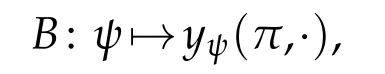
that is at the heart of the inverse problem(2.2).It is mappingL2(I)intoL2(0,T)continuously.It is also a compact operator,has a non-closed range and its inverse cannot be bounded.The goal we pursue is to assess the ill-posedness degree.We follow the methodology exposed in[8].
Tools from Fourier Series Theory enable us to know more aboutB.We construct the orthonormal basis(ek(·))k≥1inL2(I)of eigen-functions of the Laplace operatorψ→−(γ(x)ψ′)′,defined onH2∩V.The eigenvalues(λk)k≥1are all simple and positive.Ordered increasingly,the sequence is positive and grows to infinity.
For anyψ∈L2(I),we consider Fourier’s expansion
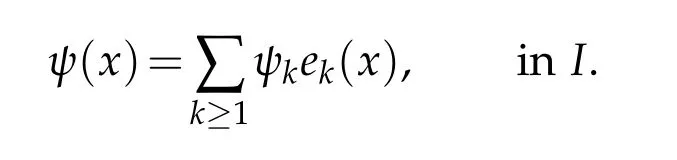
Inserting this series into the boundary value problem(2.1)yields the following expansion

Remark 2.1.Some results are needed in the sequel;they are linked to the spectral decomposition of the differential operator introduced above.Following[12,Chapter VI],we have the asymptotic formula
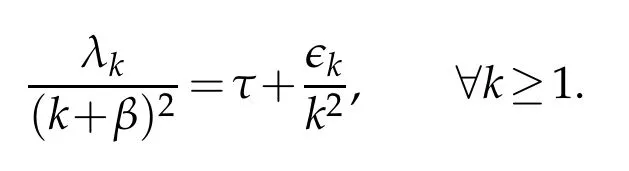
The real-numberτ>0 depends onγ(·);βis a real-number and(∊k)k≥1is a bounded sequence.Moreover,the uniform bound of the sequence(ek(π))k≥1is found in[28].The proof given there is when the conductivityγ(·)is C1.Actually,in the very case we are involved in,it can be extended to less smooth conductivities;for instance,to those that are piecewise C1.
The family(e−λkt)k≥1is linearly independent and total in R(B)(see[30]).Owing to Mntz-Szz theory,we derive the following characterization of of the range subspace
Proposition 2.1.The kernel of B is reduced to the null-subspace,i.e.N(B)={0}.The co-dimension ofR(B)in L2(0,T)is in finite.Moreover,all the functions in the closureareanalytic in]0,T]and we have

Proof.Notice that for anyk,we haveek(π)0;otherwiseek(·)≡ 0.The kernel ofBcontains therefore onlyψ=0.Then,given that(1/λk)k≥1is summable;according to the M¨untz theorem,the sequence(e−λkt)k≥1is not dense inL2(0,T).Another theorem by Clarkson and Erds[11](see also[10,Theorem 6.4])brings about more information on the closure spaceIn fact,any functionvinis analytic in]0,T]and the representation(2.4)holds true;the bound is a consequence of the fact thatv∈L2(0,T).Moreover,an in finite number of functionse−mtare necessarily outsideOtherwise it would coincide withL2(0,T).As a result,any finite dimensional subspace spanned by any sub-family,taken among those functions,belongs to a supplementary subspace ofThis yields that the co-dimension of R(B)inL2(0,T)is in finite.The proof is complete.
Now,to step further on the path of the singular values analysis for the operatorB,we need the adjoint operatorB∗which mapsL2(0,T)intoL2(I)continuously and compactly.It is easy to check out the formula
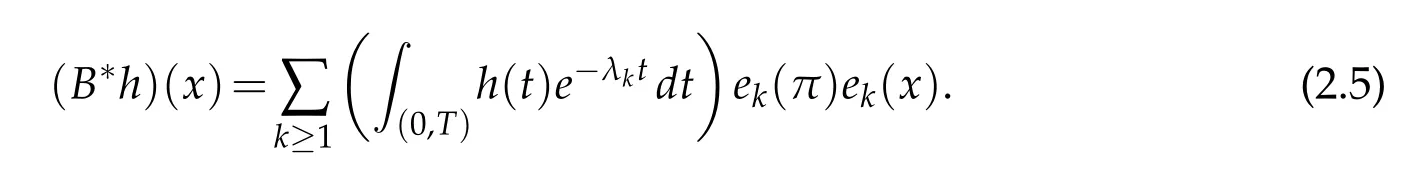
In view of Proposition 2.1,the kernel ofB∗is an in finite dimensional subspace.Indeed,its dimension is equal to the co-dimension of R(B).
2.2 Ill-posedness degree




3 Boundary data completion

3.1 Identifiability

3.2 Ill-posedness degree

4 Numerical discussion
To assess the severe ill-posedness of the Initial data recovery from Cauchy’s data,studied in Section 2,we provide some numerical illustrations.Therefore,we run some MATLAB computations to check out the estimates provided in Proposition 2.3.The singular values((σN)k)1≤k≤Nof the operatorBare calculated asthe eigenvalues of CN,theN-dimensional truncation of CT.They are represented in Fig.1,for a range ofN∈[5,25].An important fraction of the singular values are concentrated at the origin for high values ofN.The smallest ones goe towards zero with at a high speed.Observe that the singular values lower than 10−8suffer from inaccuracy.In fact,MATLAB fails to provide them and sends back incorrect values.Another feature to point out consists in the fact that if the final instantTis short,then only few singular values are not numerically zero(larger than 10−8).

Figure 1:The singular values for T=0.01(left),T=1(right).
The second illustration deals with the data completion problem adressed in Section 3.We show the flat behavior for the kernalg,at the heart of the analysis of the ill-posedness degree of our inverse problem.For constant conductivities,let us say whenγ(·)=1,it is expressed as follows
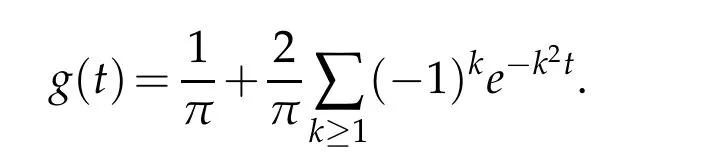
The behavior ofgis depicted in Fig.2.The representative curves ofg,g′,g′′andg′′′.The kernel is hence strongly flat and problem(3.2)is severely ill-posed.

Figure 2:The representative curves of the kernel and its first derivatives,g,g′(left)and g′′,g′′′(right).They are all flat at the vicinity of zero.
In this case of constantγ(·),Jacobi’s theta functions actually provides an elegant insight on howgand its derivatives varies at the vicinity of the origin.The kernel takes the following forms
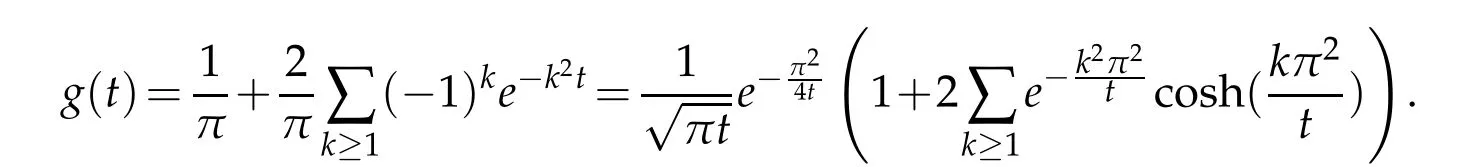
As a result,we have that for allm≥0
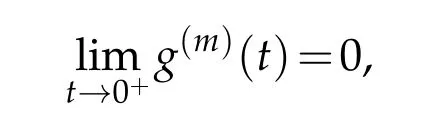
in agreement with the curves depicted in Fig.2.
5 Conclusion
The focus of the current work is the ill-posedness degree of the inverse problems(2.2),of the recovery of the initial state and(3.2),of the missing boundary data reconstruction from one sided Cauchy boundary data.The difficulties to compute a good quality solution of these problems is well known.This is a reliable indication of their severe ill-posedness.The novelty here is mainly echnical:the generality of the heat equation we work with;the conductivity is space dependent.The case where this parameter is constant has been already successfully studied(see[8,9]).Many issues related with both problems are worth to be deeply investigated,especially those related to a safe numerical approximation.Some have doubtless been treated in the specialized literature(see,eg,[2,3])and some others remain to be studied.We think particularly about the regularization strategies.What are the most efficient method to use and the best rule to fix the related parameters?
Appendix:Technical Lemmas


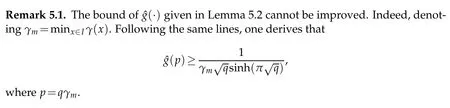
杂志排行
Journal of Mathematical Study的其它文章
- A Kind of Integral Representation on Complex Manifold
- Repdigits Base b as Difference of Two Fibonacci Numbers
- Gradient Bounds for Almost Complex Special Lagrangian Equation with Supercritical Phase
- Zeros of Primitive Characters
- s-Sequence-Covering Mappings on Metric Spaces
- On a Coupled Cahn–Hilliard System for Copolymer/Homopolymer Mixtures
