On a Coupled Cahn–Hilliard System for Copolymer/Homopolymer Mixtures
2022-04-15LaurenceCherfilsandAlainMiranville
Laurence Cherfilsand Alain Miranville
1La Rochelle Universit´e,LaSIE,UMR CNRS 7356,Avenue Michel Cr´epeau,F-17042 La Rochelle Cedex,France;
2Laboratoire de Math´ematiques et Applications,Universit´e de Poitiers,UMR CNRS 7348,Site du Futuroscope-T´el´eport 2,11 Boulevard Marie et Pierre Curie-Bˆatiment H3-TSA 61125,86073 Poitiers Cedex 9,France.
Abstract.Our aim in this paper is to study a coupled Cahn–Hilliard system for copolymer/homopolymer mixtures.We prove the existence,uniqueness and regularity of solutions.We then prove the existence of finite dimensional global attractors.
Key words:Coupled Cahn–Hilliard system,well-posedness, finite dimensional global attractors
1 Introduction
Our aim in this paper is to study a coupled Cahn–Hillard model for copolymer/homopolymer mixtures.
The original Cahn–Hilliard equation,

was initially proposed to model phase separation processes in binary alloys(see[6,7]).Since then,this equation,or some of its variants,were successfully applied to many other applications than just phase separation in alloys.We can mention,for instance,dealloying(this can be observed in corrosion processes;see[14]),population dynamics(see[11]),tumor growth(see[1,15,16,21,26]),bacterial films(see[22]),thin films(see[31]),chemistry(see[35]),image processing(see[5,8,13])and even astronomy,with the rings of Saturn(see[33]),and ecology(for instance,the clustering of mussels can be perfectly well described by the Cahn–Hilliard equation;see[24]).We refer the interested reader to[25,28]for reviews on the Cahn–Hilliard equation and some of its variants,as well as their mathematical analysis.The numerical analysis of the Cahn–Hilliard equation was addressed,e.g.,in[37,38,40,41](see also[25]for more references).
Block copolymer materials are important in engineering as they have the ability to create a wide variety of micro-structures resulting from a compromise between phase segregation and polymer architecture which prevents complete phase separation(see,e.g.,[4,12,20]).In particular,diblock copolymers have been studied from a mathematical and numerical point of view(see,e.g.,[9,17]and references therein).
In this paper,we consider a coupled Cahn–Hilliard system considered in[2,3](see also[10])to study the phase separation of mixtures consisting of a homopolymer and a copolymer.More precisely,the two phase variables were introduced to describe the macro-phase separation between the homopolymer and copolymer,as well as the micro-phase separation between the two components of the diblock copolymers.The model consists of the coupling of the Ohta–Kawasaki equation,
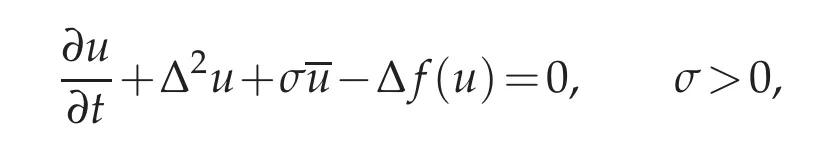
whereuis the difference betweenuand its spatial average(see[29];this equation actually is a variant of the Cahn–Hilliard–Oono equation,
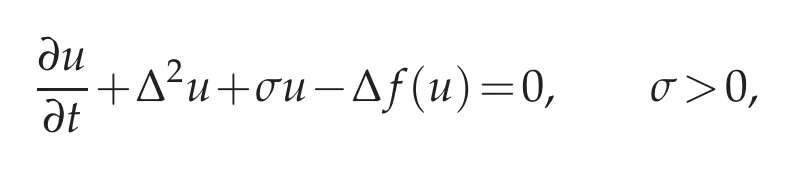
proposed in[30]to model long-ranged effects),describing microscopic phase segregation,and the Cahn–Hillard equation.A related sharp interface model was proposed in[34],where global energy minimizers were studied.More precisely,there,existence and characterization of minimizers,together with upper and lower bounds on their energy,were obtained in one space dimension.In higher space dimensions,one only has upper bounds.Another related three-components model was considered in[18,19],where the existence and stability of equilibria,which are minimizers of the energy,were studied(see also[36]for a similar model with nonlocal interactions).
Efficient numerical simulations for the coupled Cahn–Hilliard model were performed in[23],based on an uncoupled and second-order unconditionally energy stable scheme.More precisely,there,two time marching schemes were proposed and their unique solvability and unconditional energy stability were established.
In this paper,we address the mathematical analysis of the problem.More precisely,we first prove the existence,uniqueness and regularity of solutions.We then address the asymptotic behavior of the associated dynamical system,in terms of finite dimensional global attractors.
2 Setting of the problem


3 Well-posedness








4 Existence of finite dimensional global attractors




杂志排行
Journal of Mathematical Study的其它文章
- A Kind of Integral Representation on Complex Manifold
- Repdigits Base b as Difference of Two Fibonacci Numbers
- Gradient Bounds for Almost Complex Special Lagrangian Equation with Supercritical Phase
- Zeros of Primitive Characters
- s-Sequence-Covering Mappings on Metric Spaces
- Data Recovery from Cauchy Measurements in Transient Heat Transfer
