5182-O铝合金塑性成形性能表征

杨刚，张冲，娄燕山

5182-O铝合金塑性成形性能表征

杨刚1，张冲2，娄燕山2

（1. 台州科技职业学院，浙江 台州 318020；2. 西安交通大学 机械工程学院，西安 710049）

结合复杂加载状态试验、塑性和损伤断裂本构模型及有限元应用，实现AA5182-O铝合金在复杂加载状态下塑性变形和损伤断裂行为的精确表征。通过拉伸、剪切等试验，研究5182-O在剪切、单向拉伸、平面应变拉伸等复杂应力状态下的力学性能，应用pDrucker方程来表征其复杂加载状态下的塑性变形和损伤断裂特性。采用逆向工程方法实现pDrucker屈服方程和pDrucker断裂准则的精确标定。将标定后的塑性本构模型和损伤断裂准则应用到ABAQUS/Explicit中，预测不同试件的塑性变形和损伤断裂情况。通过有限元模拟与试验结果的对比，发现有限元仿真准确预测了5182-O在复杂加载状态下的力-位移曲线和损伤断裂情况。有限元模拟与试验结果的对比表明，pDrucker方程可以实现5182-O铝合金在复杂加载状态下塑性成形性能的精确表征。标定的pDrucker方程可应用于5182-O冲压成形过程的有限元分析、模具设计和工艺优化中。

冲压成形；损伤断裂；应力三轴度；Lode参数

数值模拟现在广泛用于钣金冲压成形的模具设计和工艺优化中，模拟结果的可靠性很大程度上取决于模拟中所采用材料模型的准确性。准确描述金属板材的塑性屈服、硬化和断裂，对钣金冲压成形过程有限元分析的可靠性至关重要。在过去的70年中，自Hill48各向异性屈服方程提出以来，各向异性屈服本构模型的研究已经取得了长足的进展。各向异性屈服方程主要有2类：基于主应力和基于应力不变量，其中基于主应力的典型各向异性屈服方程包括Yld91、Yld2000-2d[1]、Yld2004-14p[2]、Yld2011-27p[3]、rYld2004[4]等。最近20年，基于应力不变量的各向异性屈服方程获得越来越多的关注，这类屈服方程主要包括Cazacu-Barlat2001、Cazacu-Barlat2004、Yoon2014[5]、Hu-Chen2017[6]、各向异性Drucker[7]、pDrucker[8]等。最近10年，对各向异性的研究扩展到各向异性强化的表征，其中Stoughton等[9]、LEE等[10]、Hu等[11]、Chen等[12]的工作比较具有代表性。

随着车辆对燃油经济性、操纵性、安全性等要求的提高，铝合金、超高强度钢等轻质高强金属的应用日益广泛。轻质高强金属成形性差，冲压成形过程中容易发生损伤断裂等失效，因此，损伤断裂预测在近15年来得到越来越多的关注。提出的损伤断裂模型普遍考虑了应力三轴度、Lode参数、最大剪应力等对成形极限的影响，新提出的损伤断裂模型基本能够描述不同加载状态下的断裂应变。这类比较典型的断裂准则包括MMC、DF2012[13]、DF2014[14]、DF2016[15]等，近5年来，Mohr等[16]、Hu等[17]、Mu等[18]也提出了能够描述复杂加载状态下断裂极限的损伤断裂准则。这些断裂准则被应用到各种各样的成形过程中以预测断裂行为，并取得了比较可靠的预测结果。关于损伤断裂的最新研究进展，可参考文献[19-23]。

AA5182铝合金是Al-Mg系合金，使用范围广泛，是最有前途的合金，其耐蚀性好，焊接性优良，冷加工性较好，并具有中等强度。5182铝合金的主要合金元素为镁，具有良好的成形加工性能、抗蚀性、焊接性，强度中等，适用于制造飞机油箱、油管，以及交通车辆、船舶的钣金件，仪表、街灯支架与铆钉、五金制品、电器外壳等。文中以AA5182-O铝合金为研究对象，通过试验方法，研究其在复杂加载状态下的塑性成形性能，并基于pDrucker方程和Swift-Voce硬化准则，表征其塑性变形特性和损伤断裂特性。该本构模型通过逆向工程方法标定，以提高其表征精度。将标定的本构模型应用到ABAQUS/Explicit中，对单向拉伸、平面应变拉伸、剪切等复杂加载状态的力学反应和断裂行为进行预测，并与试验结果进行对比，通过对比结果评估pDrucker方程对其塑性变形和损伤断裂特性的表征效果。

1 力学性能试验

试验所用材料为AA5182-O，厚度为1.26 mm，为研究其复杂加载状态下的力学性能，设计了4种不同形状的试件，包括狗骨试件Ⅰ、中心孔试件Ⅱ、缺口试件Ⅲ和面内剪切试件Ⅳ，如图1所示。其中狗骨试件用于研究材料单向拉伸状态的塑性硬化特性，中心孔试件用于研究材料单向拉伸状态的断裂行为，缺口试件用于测量平面应变状态的断裂应变，面内剪切试件用于研究材料剪切状态下的断裂应变。设计的试样在材料万能拉伸试验机上在准静态条件下进行测试，测试速度参考Lou等[24]的研究结果。图1为试件加载过程中的变形和位移，通过新拓三维数字散斑采集系统完成变形过程中图片的采集和变形计算。将万能试验机上力偶所测量的力输入到新拓三维变形采集系统中，实现力和变形数据的同步同频率采集。应用新拓三维数字相关法的虚拟引伸计测量试件加载过程中的位移，虚拟引伸计的原始标距如图1所示，除了面内剪切试件的虚拟引伸计标距为60 mm外，其他3个试件虚拟引伸计的标距均为20 mm。所有试验及数据处理均在西安交通大学完成，试验系统如图2所示。

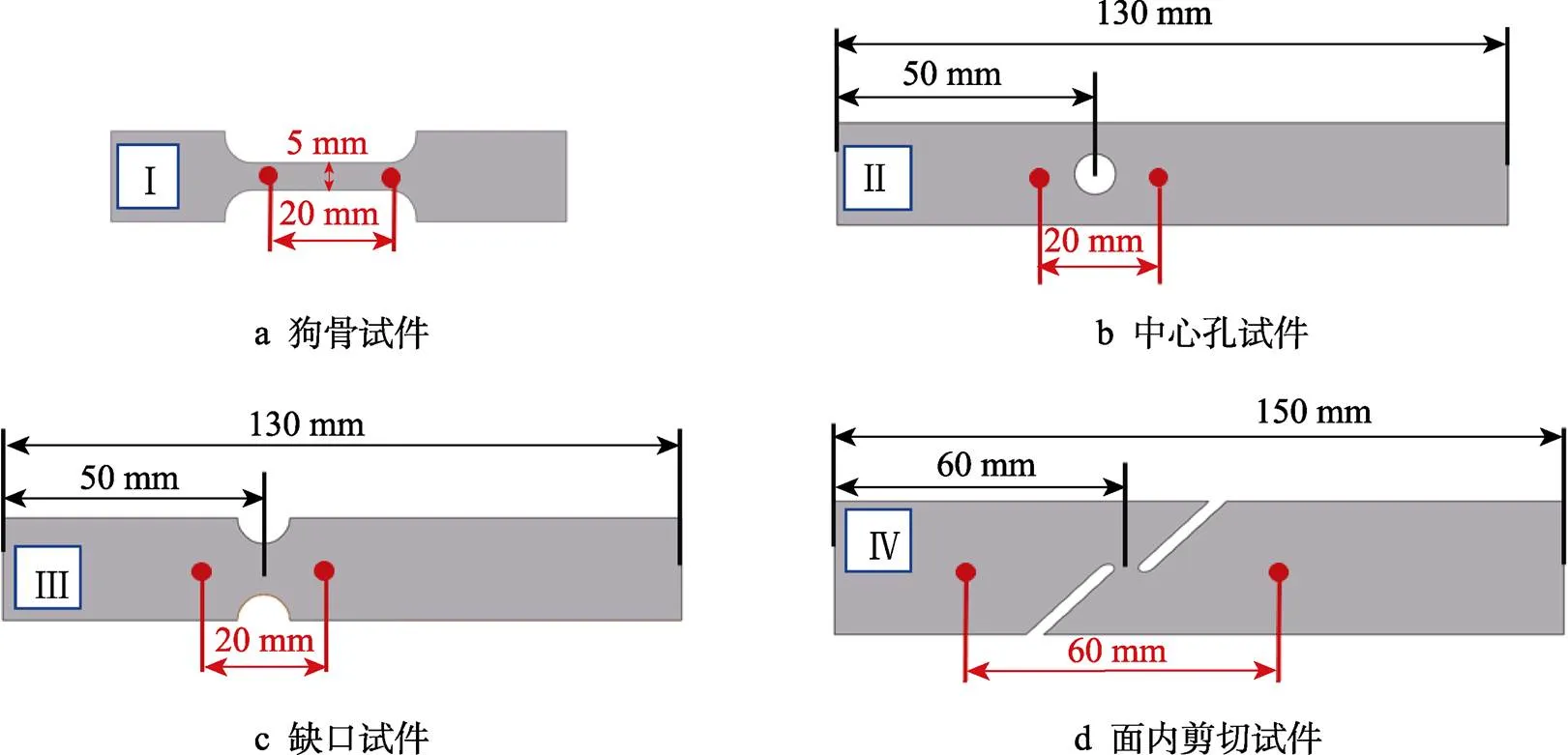
图1 不同加载状态试件

图2 力学性能试验测试及新拓三维数字图像相关法变形测量系统

狗骨试样沿轧制方向（RD）、对角方向（DD）和横向（TD）至少进行3次试验，如图3a所示，通过比较可以得出试验重复性较好，并且该材料在单向拉伸状态下的强度各向异性并不明显。图4a—c分别对比了沿3个加载方向的带孔试件、切槽试件和面内剪切试件的力-位移曲线。试验结果表明，这3个试件试验结果重复性较好，并且3个加载状态的加载方向对材料的力学性能影响不大。综上所述，该材料可以作为近似的各向同性材料。

2 本构模型

为了表征AA5182-O铝合金的塑性变形特性，文中采用Swift、Voce和Swift-Voce硬化模型来表征材料的应变强化行为，采用Drucker屈服方程表征材料在不同应力状态下的屈服特性，采用pDrucker准则来表征材料在剪切、单向拉伸、平面应变拉伸等复杂加载状态的损伤断裂特性。

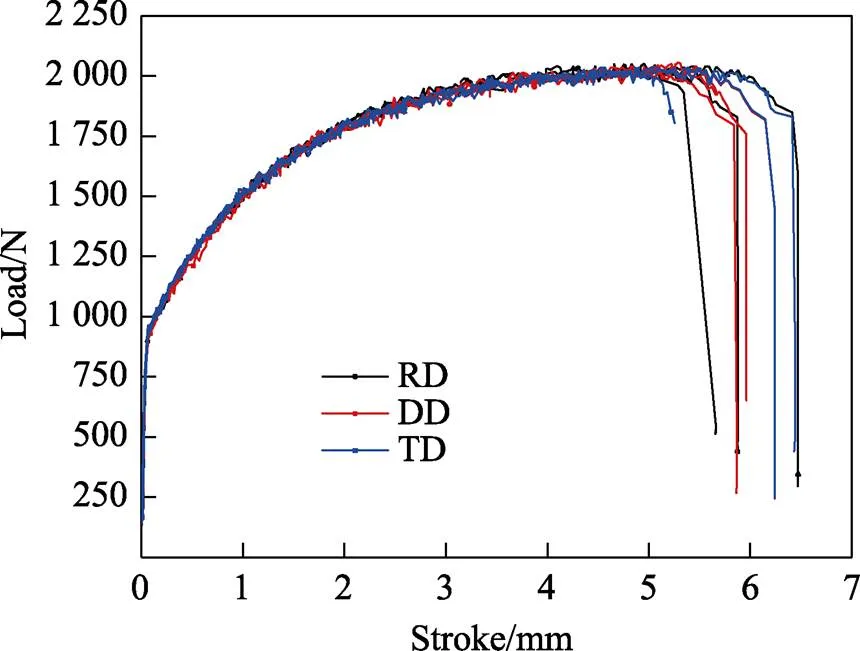
图3 狗骨试件沿3个加载方向的力-位移关系

图4 不同加载方向试验获得的力-位移曲线

2.1 应变强化特性表征

通过狗棒试件拉伸试验获得力-位移曲线如图3所示，通过理论计算得到颈缩前的真实应力-真实应变曲线，如图5的黑色曲线所示。在有限元模拟过程中，硬化曲线常用Swift和Voce模型来拟合表征，其表达式见式（1）—（2）：

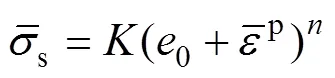
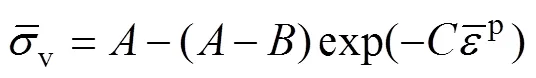
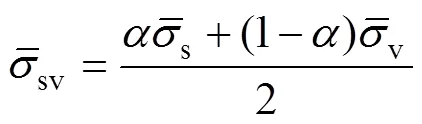
表1 狗棒试件3个加载方向的屈服应力和Swift、Voce模型参数

Tab.1 Yield stress and parameters of the Swift and Voce models of dog-bone specimens along three stress directions

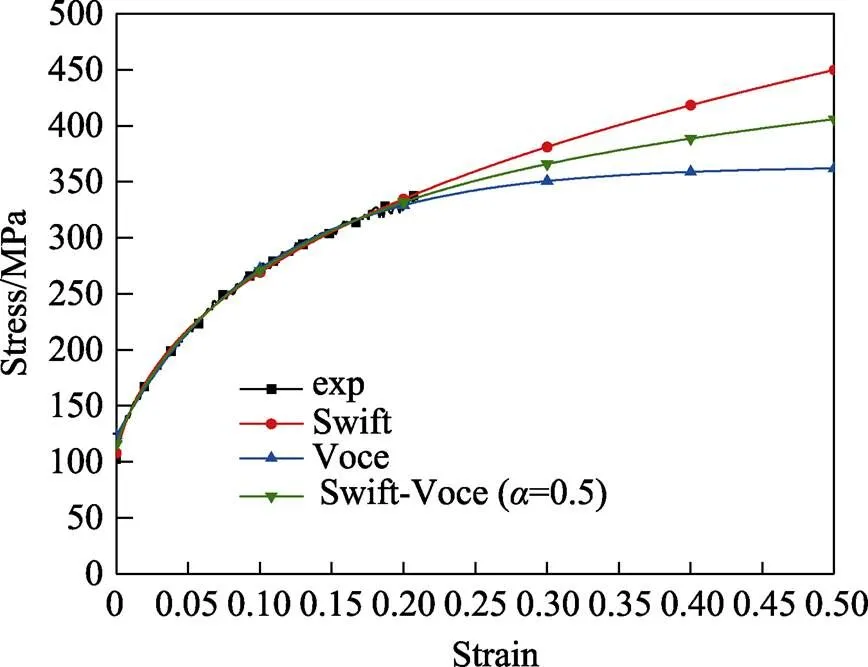
图5 硬化模型预测曲线与试验数据的对比

2.2 屈服特性表征

为了表征AA5182-O在复杂加载条件下的屈服行为，文中采用静水压力修正的Drucker方程[10]，标记为pDrucker，如式（4）所示：

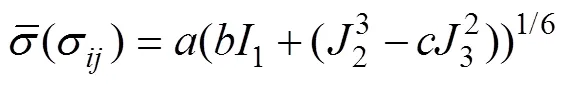
式中：1、2、3为应力不变量；、、为材料塑性变形行为参数。主应力可以通过应力三轴度、Lode参数和von Mises等效应力来计算[25]，公式见式（5）：

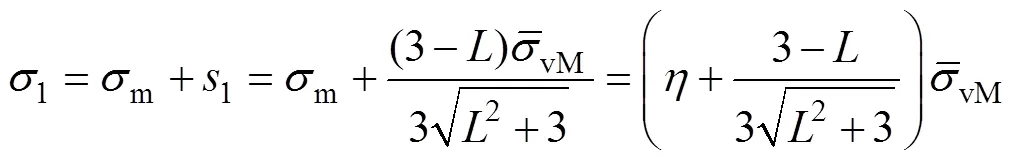
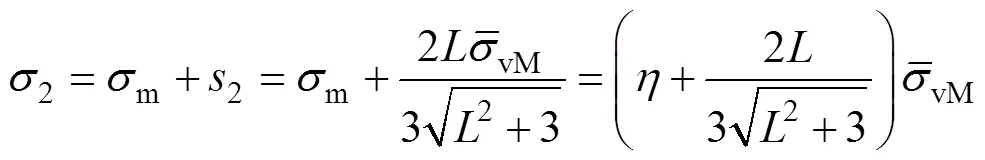
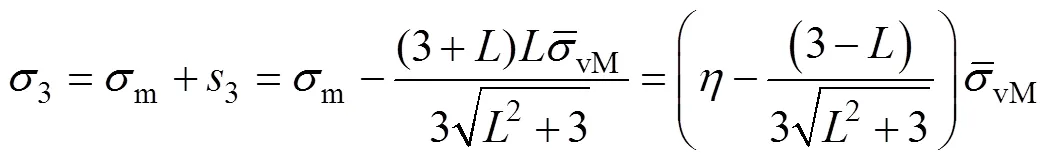
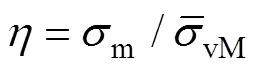
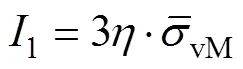
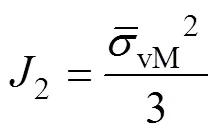
式中：s为偏应力张量。把式（8）—（10）代入式（4）可得：

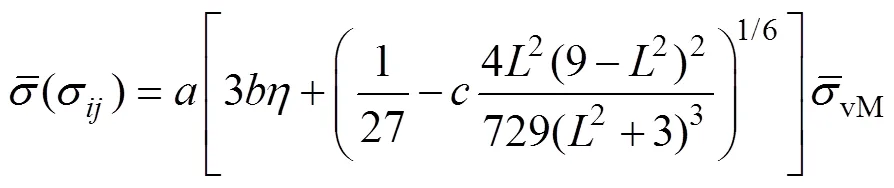
硬化曲线通过单向拉伸试验获得，则pDrucker方程参数的计算公式见式（12）。

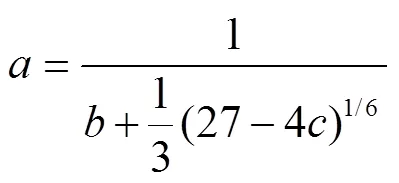
pDrucker屈服方程预测的屈服面与von Mises和Tresca屈服方程预测的屈服面对比如图6所示。在对比中，假设静水压力影响可以忽略不计，因此pDrucker方程退化为Drucker方程。Drucker方程可以通过其中的参数调整材料在平面应变或剪切状态的屈服强度，从而能够更为精确地表征材料在复杂应力状态下的塑性变形行为。

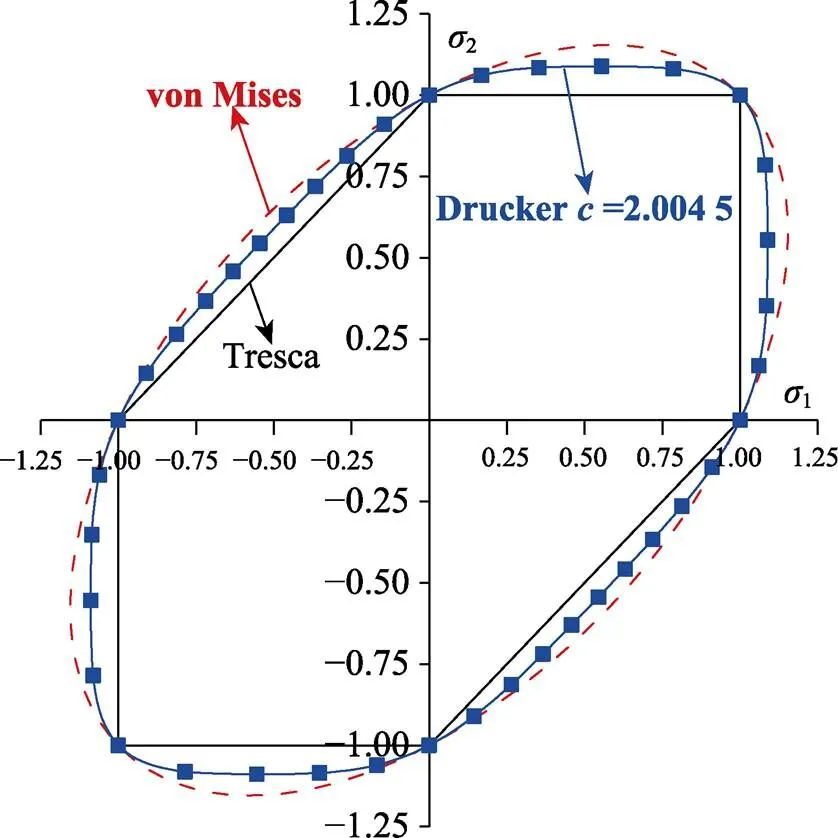
图6 典型屈服面对比

2.3 损伤断裂特性表征

为了表征AA5182-O在复杂应力状态的损伤断裂行为，文中采用pDrucker方程，其表达式见式（13）：

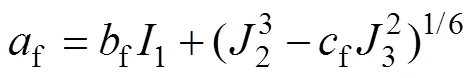
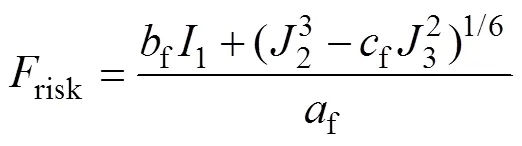
当risk<1.0时，不会发生断裂，当risk=1.0时，材料发生断裂失效。

3 塑性变形特性表征结果分析

为了表征AA5182-O的塑性变形特性，需要确定式（3）中SV模型中的参数和pDrucker模型中参数和。用于调整静水压力的影响，用于表征第三应力不变量的影响，决定了在超过0.21颈缩应变的大应变下的应力-应变曲线。这3个参数通过逆向工程方法确定，即通过对比中心孔试样、缺口试样和面内剪切试样在数值模拟和试验载荷-位移曲线的误差来确定。将图1b—d中3个试件的力-位移曲线试验结果与数值模拟进行比较，各试件的误差通过式（15）计算。预测误差由平均力归一化，因此不同强度试件之间的误差对总误差的贡献相等。3个测试的总误差用Total error表示，代表3个试样预测误差的总和，通过总误差的最小化，实现塑性模型本构参数的优化。

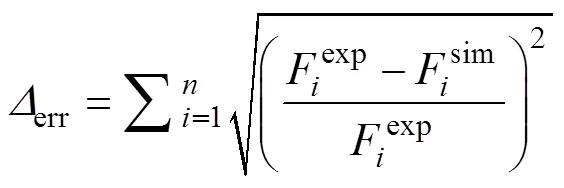
表2 逆向工程优化后的SV和pDrucker模型的参数值

Tab.2 Parameters of SV and pDrucker models optimized by inverse engineering method

将标定后pDrucker屈服方程屈服面与Tresca和von Mises进行比较，如图6所示。比较结果表明，pDrucker屈服函数预测的剪切和平面应变强度应力比Tresca屈服函数高4.44%，比von Mises屈服函数低5.70%。此外，Drucker屈服面在单轴拉伸、等双轴拉伸、单轴压缩和等双轴压缩时的曲率介于Tresca和von Mises屈服函数预测的曲率之间。

将标定后的SV硬化方程和pDrucker屈服方程应用到ABAQUS/Explicit中，模拟中心孔试件、切槽试件和剪切试件的加载过程，将预测的力-位移曲线与试验结果进行对比，如图7所示。图7a的结果表明，von Mises和Drucker函数可以高精度地预测中心孔试件的强度，但Tresca屈服函数低估了该试件的强度。在断裂前的大部分变形阶段，pDrucker屈服函数的预测值比von Mises屈服函数的预测值更接近试验结果。对于图7b中的切槽试件，当位移小于1.6 mm时，von Mises函数预测的强度具有良好的一致性，但当位移超过1.6 mm时，von Mises方程预测的结果比试验结果大，误差也随之变大，尤其是在最大载荷之后。Tresca屈服函数预测的试件强度要比试验结果低得多，尤其是在大变形时。对于Drucker屈服函数，预测的力-位移曲线与试验结果吻合得非常好，从塑性变形开始到断裂的误差基本小于1%，可以忽略不计。对于图7c的面内剪切试件，Tresca函数低估了该试件的强度，而von Mises函数在行程小于2.4 mm时预测的承载能力比试验结果要高出很多，而von Mises的预测结果在2.5 mm后远低于试验结果。pDrucker函数预测的力-位移曲线最大误差小于2%，但与其他2个屈服函数相比，预测精度提高非常大，总体误差是可以接受的。这3种试件试验和有限元预测的力-位移曲线的比较结果，证明文中所采用的SV硬化方程和pDrucker屈服函数能够高精度地表征AA5182-O在不同加载状态下的塑性变形行为，逆向工程方法能够准确标定SV硬化模型和Drucker屈服函数的参数。

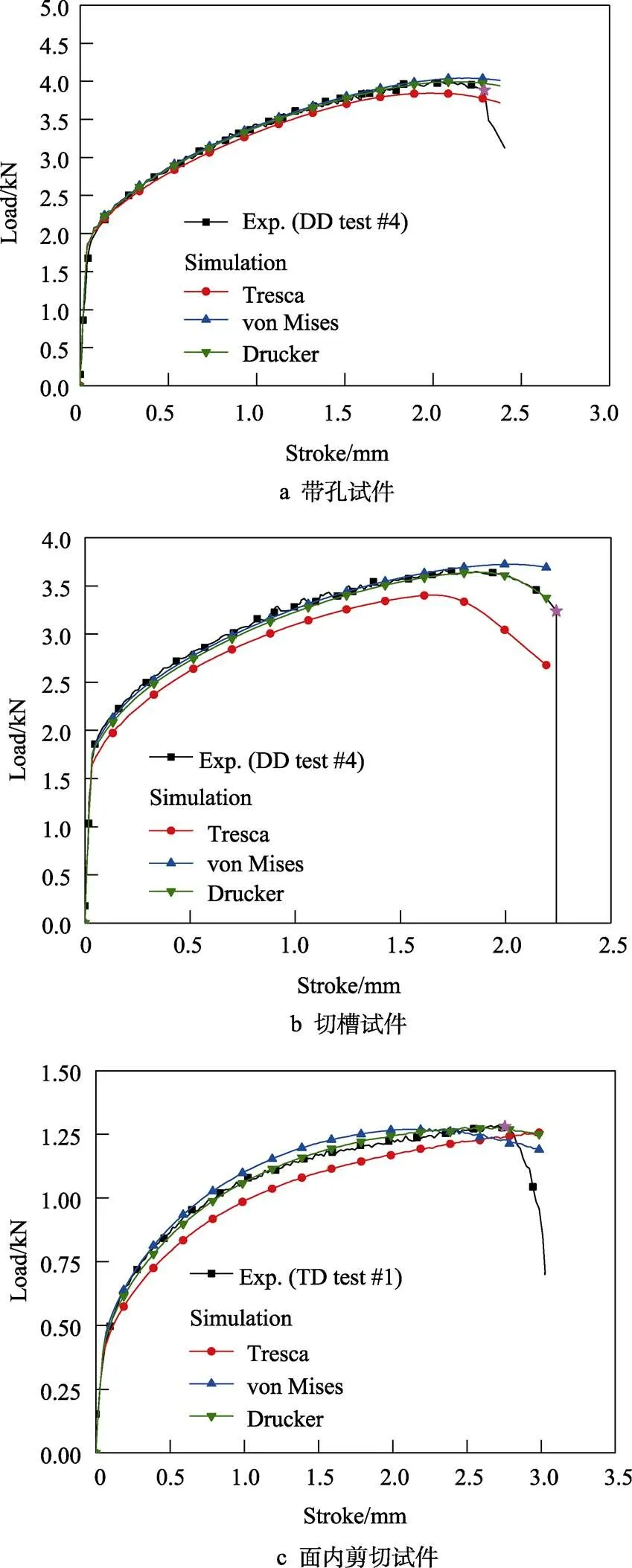
图7 预测的力-位移曲线与试验结果的对比

4 损伤断裂特性表征结果分析

文中采用式（13）所示的pDrucker方程来表征AA5182-O在复杂应力状态下的断裂特性。pDrucker断裂准则的参数通过逆向工程的方法来优化，即通过比较有限元预测的断裂位移与试验断裂位移，最小化有限元预测误差的方法，实现pDrucker断裂准则参数的标定和优化。参数优化的结果为f=0.207 2，f=0.022 0和f=2.629 4。应用表1的SV硬化模型参数和pDrucker屈服方程参数，以及本小节优化的pDrucker断裂准则参数，通过ABAQUS/Explicit完成图1b—d中的试件加载过程和断裂模拟，将有限元预测的结果与试验结果进行比较，从而验证pDrucker断裂准则对AA5182-O在复杂加载状态下损伤断裂行为预测的可靠性。

图8a—c为中心孔试件、切槽试件和面内剪切试件有限元预测的力-位移曲线和断裂位移与试验结果的对比。对于图8a所示的中心孔试件，试验的断裂位移为2.29 mm，有限元预测结果为2.34 mm，误差小于2.2%。对于图8b所示的切槽试件，试验的断裂位移为2.24 mm，有限元预测结果为2.12 mm，误差小于5.4%。对于图8c所示的面内剪切试件，试验的断裂位移为2.76 mm，有限元预测结果为2.77 mm，误差小于0.4%。3个不同应力状态下断裂预测的平均误差为2.7%，最大误差小于5.4%，因此，文中所采用的pDrucker断裂准则能够精确地预测AA5182-O在复杂应力状态下的断裂行为。另外，图8所示的有限元断裂位置预测结果与试验观察结果证明pDrucker断裂准则能够精确地预测断裂开始的位置。

5 结语

采用试验、理论和有限元分析的方法，系统研究了AA5182-O在复杂应力状态下的塑性变形和损伤断裂特性。研究结果表明，AA5182-O的塑性成形特性受应力状态影响非常明显；SV硬化模型和Drucker屈服方程能够准确表征该合金在复杂应力状态下的塑性变形特性；pDrucker断裂准则能够精确描述研究对象在复杂应力状态下的损伤断裂行为；逆向工程方法能够实现本构模型参数的精确表征。文中所采用的试验方法、SV硬化方程、pDrucker屈服方程和损伤断裂准则，可以应用到轻质高强材料塑性成形特性的表征中，提高轻质高强金属塑性成形模具设计、工艺分析和优化的可靠性。

[1] Barlat F, Brem J C, Yoon J W, et al. Plane Stress Yield Function for Aluminum Alloy Sheet-Part I: Theory[J]. International Journal of Plasticity, 2003, 19: 1297-1319.

[2] Barlat F, Aretz H, Yoon J W, et al. Linear Transformation-Based Anisotropic Yield Functions[J]. International Journal of Plasticity, 2005, 21: 1009-1039.

[3] Aretz H, Barlat F. New Convex Yield Functions for Orthotropic Metal Plasticity[J]. International Journal of Non-Linear Mechanics, 2013, 51: 97-111.

[4] LOU Yan-shan, Zhang Sai-jun, Yoon J W. A Reduced Yld2004 Function for Modeling of Anisotropic Plastic Deformation of Metals under Triaxial Loading[J]. International Journal of Mechanical Science, 2019, 161/162: 105027.

[5] Yoon J W, LOU Yan-shan, Yoon J H, et al. Asymmetric Yield Function Based on the Stress Invariants for Pressure Sensitive Metals[J]. International Journal of Plasticity, 2014, 56: 184-202.

[6] Hu Qi, Li Xi-feng, Han Xian-hong, et al. A Normalized Stress Invariant-Based Yield Criterion: Modeling and Validation[J]. International Journal of Plasticity, 2017, 99: 248-273.

[7] LOU Yan-shan, Yoon J W. Anisotropic Yield Function Based on Stress Invariants for BCC and FCC Metals and Its Extension to Ductile Fracture Criterion[J]. International Journal of Plasticity, 2018, 101: 125-155.

[8] LOU Yan-shan, Zhang Sai-jun, Yoon J W. Strength Modeling of Sheet Metals from Shear to Plane Strain Tension[J]. International Journal of Plasticity, 2020, 134: 102813.

[9] Stoughton T B, Yoon J W. Anisotropic Hardening and Non-Associated Flow in Proportional Loading of Sheet Metals[J]. International Journal of Plasticity, 2009, 25: 1777-1817.

[10] Lee E H, Choi H, Stoughton T B, et al. Combined Anisotropic and Distortion Hardening to Describe Directional Response with Bauschinger Effect[J]. International Journal of Plasticity, 2019, 122: 73-88.

[11] Hu Qi, Yoon J W, Manopulo N, et al. A Coupled Yield Criterion for Anisotropic Hardening with Analytical Description under Associated Flow Rule: Modeling and Validation[J]. International Journal of Plasticity, 2021, 136: 102882.

[12] Chen Zhe, Wang Yue, LOU Yan-shan. User-Friendly Anisotropic Hardening Function with Non-Associated Flow Rule under the Proportional Loadings for BCC and FCC Metals[J]. Mechanics of Materials, 2022, 165: 104190.

[13] LOU Yan-shan, HUH H, LIM S, et al. New Ductile Fracture Criterion for Prediction of Fracture Forming Limit Diagrams of Sheet Metals[J]. International Journal of Solids and Structures, 2012, 49: 3605-3615.

[14] LOU Yan-shan, YOON J W, HUH H. Modeling of Shear Ductile Fracture Considering a Changeable Cut-Off Value for the Stress Triaxiality[J]. International Journal of Plasticity, 2014, 54: 56-80.

[15] LOU Yan-shan, CHEN Lin, CLAUSMEYER T, et al. Modeling of Ductile Fracture from Shear to Balanced Biaxial Tension for Sheet Metals[J]. International Journal of Solids and Structures, 2017, 112: 169-184.

[16] MOHR D, MARCADET S J. Micromechanically-Motivated Phenomenological Hosford-Coulomb Model for Predicting Ductile Fracture Initiation at Low Stress Triaxiality[J]. International Journal of Solids and Structures, 2015, 67/68: 45-55.

[17] HU Qi, LI Xi-feng, HAN Xian-hong, et al. A New Shear and Tension Based Ductile Fracture Criterion: Modeling and Validation[J]. European Journal of Mechanics-A/Solids, 2017, 66: 370-386.

[18] MU Lei, ZANG Yong, WANG Yuan, et al. Phenomenological Uncoupled Ductile Fracture Model Considering Different Void Deformation Modes for Sheet Metal Forming[J]. International Journal of Mechanical Science, 2018, 141: 408-423.

[19] 顾彬, 何霁, 李淑慧, 等. 金属板料各向异性断裂模型及断裂实验研究进展[J]. 塑性工程学报, 2019, 26(1): 1-14.

GU Bin, HE Ji, LI Shu-hui, et al. Research Progress on Anisotropic Fracture Models and Fracture Tests for Sheet Metals[J]. Journal of Plasticity Engineering, 2019, 26(1): 1-14.

[20] 贾哲, 穆磊, 臧勇. 金属塑性成形中的韧性断裂微观机理及预测模型的研究进展[J]. 工程科学学报, 2018, 40(12): 1454-1467.

JIA Zhe, MU Lei, ZANG Yong. Research Progress on the Micro-Mechanism and Prediction Models of Ductile Fracture in Metal Forming[J]. Chinese Journal of Engineering, 2018, 40(12): 1454-1467.

[21] 李非凡, 雷丽萍, 方刚. 镁合金塑性变形及延性断裂预测研究进展(下)——延性断裂模型的开发及应用[J]. 塑性工程学报, 2020, 27(2): 1-12.

LI Fei-fan, LEI Li-ping, FANG Gang. Research Advances of Plastic Deformation and Ductile Fracture Prediction of Magnesium Alloys Part Ⅱ: Development and Application of Ductile Fracture Models[J]. Journal of Plasticity Engineering, 2020, 27(2): 1-12.

[22] 詹梅, 李锐, 郑泽邦, 等. 旋压成形损伤断裂缺陷预测研究进展[J]. 精密成形工程, 2019, 11(5): 13-29.

ZHAN Mei, LI Rui, ZHENG Ze-bang, et al. Research Progress on Fracture Prediction in Spin-Forming[J]. Journal of Netshape Forming Engineering, 2019, 11(5): 13-20.

[23] HU Qi, ZHANG Fei-fei, LI Xi-feng, et al. Overview on the Prediction Models for Sheet Metal Forming Failure: Necking and Ductile Fracture[J]. Acta Mechanica Solida Sinica, 2018, 31(3): 259-289.

[24] LOU Yan-shan, Huh H. Prediction of Ductile Fracture for Advanced High Strength Steel with a New Criterion: Experiments and Simulation[J]. Journal of Materials Processing Technology, 2013, 213: 1284-1302.

[25] LOU Yan-shan, HUH H. Extension of a Shear Controlled Ductile Fracture Model Considering the Stress Triaxiality and the Lode Parameter[J]. International Journal of Solids and Structures, 2013, 50: 447-455.

Characterization on Plastic Forming Properties of 5182-O Aluminum Alloy

YANG Gang1, ZHANG Chong2, LOU Yan-shan2

(1. Taizhou Vocational College of Science & Technology, Zhejiang Taizhou 318020, China; 2. School of Mechanical Engineering, Xi'an Jiaotong University, Xi'an 710049, China)

The work aims to precisely characterize the plastic deformation and damage fracture of AA5182-O aluminum alloy under complex stress states in combination with the test complex stress state, plastic and damage fracture constitutive model and finite element application method. Tensile and shear tests were conducted to study the mechanical properties of 5182-O under complex stress states of shear, uniaxial tension and plane strain tension. The plastic deformation and damage fracture behavior under complex stress states were characterized by the pDrucker equation. The accurate calibration of pDrucker yield equation and pDrucker fracture criterion was realized by reverse engineering method. The calibrated plastic constitutive model and damage fracture criterion were applied to ABAQUS/Explicit to predict the plastic deformation and damage fracture of different specimens. The comparison between finite element simulation and test results showed that the finite element simulation could accurately predict the stress-displacement curve and damage fracture of 5182-O under complex stress states. The comparison between finite element simulation and test results shows that pDrucker equation can accurately characterize the plastic formability of 5182-O aluminum alloy under complex stress states. The calibrated pDrucker equation can be applied to the finite element analysis, die design and process optimization of 5182-O stamping process.

stamping; damage fracture; stress triaxiality; Lode parameter

10.3969/j.issn.1674-6457.2022.04.008

TG381

A

1674-6457(2022)04-0061-08

2022-01-31

国家自然科学基金（52075423）；国家自然科学基金“叶企孙”科学基金（U2141214）；2021台州市第二批工业类科技计划（21gyb34）

杨刚（1989—），男，硕士，讲师，主要研究方向为铝合金冲压成形。

娄燕山（1983—），男，博士，教授，主要研究方向为塑性成形。

责任编辑：蒋红晨