基于改进蚁群算法的客运站到发线运用优化研究
2022-04-15王林杰
王林杰
(兰州交通大学交通运输学院,甘肃 兰州 730070)
随着我国高铁的蓬勃发展,截止2020年9月,“八纵八横”高铁网络主骨架已搭建七成,2020年底我国高铁里程达到38 000 km。高速铁路具有发车间隔小、作业时间短、作业过程简单以及列车开行密度大、进出站频率高等特点,因此对车站客运服务质量和列车正点率要求较高。到发线的运用直接关系着站场能力的利用,合理、高效地运用到发线能够促进客运站安全、顺利地完成各项客运作业。
关于到发线的优化问题有很多学者做了研究。部分研究把客运站优化问题划分为3个子目标问题,其中谢楚农等[1]建立了多目标模型,并且使用分支定界法来求解模型;郭吉安等[2]建立以均衡运用到发线、缩短旅客走行距离和减小列车在站作业时间为多目标的优化模型。林志安[3]等用捕食禁忌搜索算法来求解模型。部分研究建立了0-1整数规划的非线性客运站优化模型,可以自动制定车站到发线的运用计划,但没有考虑到发线的均衡性问题。吕红霞等[4]建立了0-1整数到发线优化模型,并采用了蚁群算法求解。何林[5]等引用时间片理念,以旅客走行距离最小为目标,规定了到发线权值大小,并以最大权值为目标建立了车站到发线运用模型。李琦[6]以旅客服务质量为目标,通过使用自适应克隆算法来优化其模型。青学江等主要研究了区段站到发线的优化问题,并采用遗传算法来求解模型。李涛等通过改进遗传算法来解决高铁客运站的到发线优化模型,改进算法达到了较好的效果。部分研究以优化到发线的排序为目标建立了优化模型。
以上研究大多数是基于普通的优化算法来求解的,这些方法求解过程复杂而且效率很低,无法解决更复杂的数学模型。也有部分研究是基于智能算法来优化模型,但这些智能算法对于复杂的大规模模型,收敛速度较慢,针对一些特大规模的高铁车站,无法实现客运站的智能化目标。为了实现铁路客运站作业智能化,通过改进蚁群算法的初始信息素、信息素更新规则、启发式信息和状态转移规律来解决大规模的优化问题,算法收敛速度很快,能够快速、高效、准确地求解,找到较优的到发线运用计划。
1 列车占用到发线问题分析
到发线运用是指在一定时间内,根据列车种类及作业性质,考虑各种时间标准的限制并协调咽喉进路,为图定旅客列车分配合适的作业股道、停靠站台并规定其相应的占用时间安排每列车合理地使用到发线,保证所有列车都能够按时完成作业计划。因此到发线的使用需要满足以下约束条件:(1)同一时间一条到发线只能接发1列车;(2)站台两侧的到发线应不同时安排其他列车在站作业;(3)占用同一到发线的相邻列车应该满足的最小安全间隔要求;(4)有换乘关系的两列车尽量安排在同站台停靠;(5)为车站方便、高效的组织作业,应该按照到发线的固定方案使用;(6)到发线使用时应尽量减少交叉干扰。上述条件是铁路安全作业的根本保障,在日常铁路生产中必须满足。
2 到发线运用优化模型构建
合理的到发线运用计划有利于保证列车不间断接发车,减少列车等待时间,合理分配车站设备能力,相互较少列车作业交叉干扰,保证列车顺利、安全、高效地通过车站且快速、合理地完成旅客乘降作业。所以到发线的运用优化可以从均衡使用车站设备、提高行车作业、提高旅客服务质量3个方面为目标进行研究。
2.1 模型构建
设客运车站站台集合为Q={1,2,…,q,…,u},其q为车站站台的编号顺序,u为站台数量总和;设列车集合P={1,2,…,p,…,m},其中p为列车到站的编号顺序,m为列车数量的总和;设到发线集合K={1,2,…,k,…,n},其中k为车站到发线的编号顺序,n为到发线数量的总和。
列车占用到发线状态用决策变量0-1来表示,xpk为到站列车p占用到发线的状态,取值表示为
(1)
2.2 优化模型
车站到发线运用计划的优化是为了列车能够正点、准时和安全地完成车站内的各项客运作业,在不影响其他线路和列车的作业计划前提下,高效地完成路局下达的运输生产任务,同时要考虑到旅客的满意度,提高为旅客服务的质量。因此,为了使高铁车站高效、安全地完成运输生产任务,以所有在站列车占用到发线时间最优和均衡使用到发线为目标。建模如下
(2)
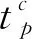
2.3 条件约束
根据到发线运用的基本原则与车站其他设备对其的限制,服从以下约束。
(1)某列车占用某条到发线,该列车不得转入其他到发线上直至列车离开车站。约束条件如下
(3)
(2)同一时间一条到发线只能接发1列车。约束条件如下
(4)
(3)同一到发线接发相邻列车时需满足最小安全间隔时间。约束条件如下:
|x(p+1)kts(p+1)-xpktep|≥T
(5)
式中:T为相邻列车占用同一到发线的最小安全间隔时间,本文取值为10 min。
(4)到发线使用时应尽量减少交叉干扰。组织平行作业来减小交叉干扰。约束条件如下
xpk≤1-hpkjp=1,2,…,m;k=1,2,…,m
(6)
式中:当p列车占用到发线k与其他作业j相互产生干扰时,hpkj=1,否则hpkj=0。
(5)有换乘关系的两列车尽量安排在同站台停靠。约束条件如下
(7)
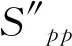
(6)两相邻站台同侧到发线的列车应当满足一定的时间间隔,防止旅客检票进站时两流线相互干扰。约束条件如下

(8)

3 改进蚁群优化算法
3.1 AOC算法改进
(1)改进初始信息素。
基本AOC算法在初始阶段信息素是一个定值,蚂蚁在初始搜索时具有盲目性,会导致搜索时间加长。因此提出一种信息素改进的方法,根据目前节点、下一节点与起点之间的位置距离计算初始信息值,公式如下
(9)
式中:dSE为从起点到终点的距离;dSi为从出发点到目前节点的距离;dij为目前节点到下一节点的距离;djE为下一节点到终点的距离;α0为常数;C为下一节点的集合。从上面公式可以看出当分母越小,信息素越大。为了避免算法在初始时盲目搜索,改善搜索效率,提出了根据相互位置关系设定初始信息素的不均衡分布。
(2)改进信息素更新规则。
信息素更新主要描绘了蚂蚁分泌的化学物质随时间的变化规律。蚁群在完成一次搜索循环后进行更新路径。全部的蚂蚁完成迭代后,所有的路径信息素都将更新,可以在所有的路径上找到最差结果与最优结果,如公式(10)所示,由当前结果可以对后续的迭代进行指导。最差的解将可以对其表述处理,加快了算法的收敛速度。
(10)
式中:Lbest为目前最优路径的长度;Lworst为目前最差路径的长度;为了防止算法停止,将信息素的范围设定为[τmin,τmax],如公式(11)所示
(11)
(3)改进启发式信息。
基本AOC算法的启发式信息是与下个节点到终点的距离成反比,这样有助于蚂蚁选择最优的路径。但是如果不考虑当前位置和下个位置的状况,蚂蚁选择的路径不一定为最优路径,而且在算法搜索后期为了加快算法收敛速度,会影响启发式信息对路径选择的指导作用。本文采用引入阻尼系数来改进启发式信息,如公式(12)所示
(12)
其中:
(13)
式中:NCmax为迭代次数的最大设定值,NC为目前的迭代次数。
(4)改进状态转移规律。
使用伪随机状态转移规律来改善算法质量和搜索效率。假设在t时刻蚂蚁k在i节点,那么蚂蚁k在t+1时刻的节点位置为
(14)
式中:q0为状态转移规律的转换率,取值在0-1之间;q为随机自然数,当q≤q0时,下个节点的位置直接由启发式信息和最大的信息素浓度值来确定。
随机选择模式的概率与确定性选择由q0直接决定。采用自适应计算q0的算法,q0的值由迭代次数Nc和最优路径的长度Lbest来计算,如公式(15)所示
(15)
式中:b为0-1之间的常数;N0为迭代次数阈值。
3.2 AOC算法流程
引入车站到发线时间片概念,改进的蚁群算法求解到发线运用流程如下:
Step1:参数初始化。包含的参数有蚂蚁数量m、算法最大迭代次数NCmax、起始位置S、蚁群信息素强度Q、信息素启发式因子α、期望启发式因子β等。m取100,NCmax取100,Q取200。
Step2:算初始信息素。常数α0取0.5,将dsi,dij,djE分别代入基本算法公式中计算。
Step3:到发线选择。假设蚂蚁k在t时刻上,此时列车在i到发线选择节点上,利用公式(14)由τij和α计算出到下一到发线节点的选择路径,在t+1时刻上到发线节点选择根据公式(14)计算出。
Step4:启发式信息和信息素的更新。当完整的到发线路径被建立后,将对启发式信息和信息素更新,将Δτij(t),ρ,1-ρ根据基本算法公式更新信息素,再根据公式(12)更新启发式信息。
Step5:全局更新信息素。当蚁群中所有的蚂蚁搜索完成一次后,找出此迭代过程中的最差和最优到发线路径,然后由基本算法公式和式(10)调整最优和最差到发线上的信息素。
Step6:自适应调整q0。当Nc大于N0时,可由当前Lbest,NCmax,dSE通过公式(15)计算出q0。
Step7:搜索结束。判断是否满足最优条件,如满足,输出最优解;否则将禁忌清单清除,使得Nc=Nc+1,转到step3继续计算。
4 算例分析
为了验证算法和模型的可行性,采用定西北站的运行图数据,选用高铁客运站9∶00~12∶00的数据来计算验证。在此时间段内共有18列车在该站办理旅客乘降作业,该站共有2条正线,4条到发线,2个站台。其中第I,II号为正线,只办理通过作业;第3,5号到发线接下行列车;第4,6号到发线接上行列车;1,2号站台分别分布在4,6和3,4之间。因为该车站上下行到发线都是同等级的,所以本文中的列车占用到发线的权值cpk都设为1。蚁群规模为m=100,最大迭代次数NCmax=100,信息素启发式因子α=0.8,期望启发式因子β=2.5。常数Q=200。算法在matlab2016b中求解,最终最优解稳定在6 967.56。由于0-1整数规划为离散型函数,目标值的收敛曲线如图1所示。模型收敛速度很快,在第51代的时候找到最优值。可以看出改进的算法具有良好的收敛效果,可以满足求解更加复杂的大规模寻优问题。

图1 改进蚁群算法收敛曲线
通过整理数据得到该站的到发线运用计划,列车序号是根据列车的到站时间先后排列的,如表1所示。
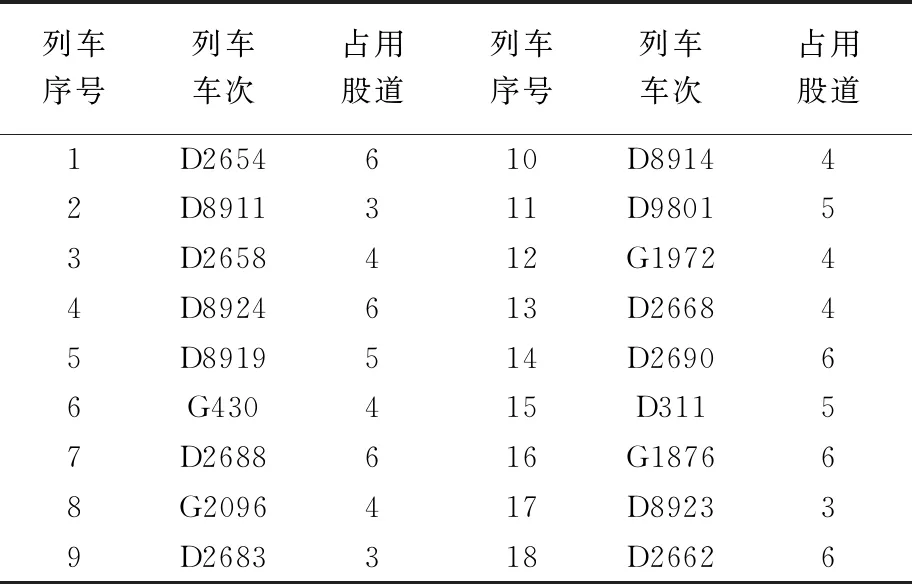
表1 客运站9∶00~12∶00的到发线运用计划
从该算例的结果可以看出,在目标函数最优的情况下上行列车均匀分布在4,6股道,下行列车均匀分布在3,5股道上,上下行列车均匀的分布在每条股道上,达到了到发线的均衡使用要求。主要用到发线占用率、占用时长标准差和各占用时间来评价到发线适应性指标。

表2 各到发线在9∶00~12∶00的占用累积时间
(1)到发线占用率。

(2)各条到发线在9∶00~12∶00的平均被使用时间。

(3)到发线占用时间标准差。
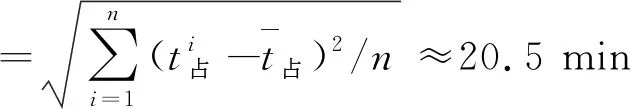
从上面计算的各项指标结果可以看出,每条到发线的利用效率比较高。模型和算法能够满足列车在车站按时按点地完成作业,用改进的蚁群算法可以快速地找到满足条件最优方案,为将来新建车站制定到发线运用计划提供一种参考方法。
5 结束语
在已有研究的基础上,采用相应的模型和算法来研究车站到发线运用计划,建立了以均衡使用到发线和列车在到发线停留时间最短为目标的0-1整数非线性规划模型,且采用改进蚁群算法进行求解,最后根据算例结果可以看出模型和算法能够快速地找到满足条件的方案。但目前是根据列车运行图的图定时间来研究的,没有考虑列车正晚点的影响,而且未考虑特殊情况下因出现大客流而导致列车密集到达的情况,该模型无法提供到发线运用计划的临时调整,在后期的研究中可以深入探究。
