长大桥梁健康监测系统数据灰色关联度分析
2022-04-15刘勇,杨康
刘 勇,杨 康
(1.江苏省交通工程建设局,江苏 南京 210004;2.苏交科集团股份有限公司工程检测中心,江苏 南京 211106)
在自动控制与机械工程领域内,为了提高监测系统自诊断的性能,需要充分利用监测系统的冗余信息,包括硬件设备冗余、时序冗余、分析计算冗余[1];这同样适用于桥梁结构健康监测领域。充分发掘数据的冗余性,提升鲁棒性,可以极大地促进监测系统自诊断技术的智能化、体系化。一般来说,长大桥梁健康监测系统预算成本充足,监测项目完整,测点多,因此硬件是欠冗余的,同时,长大桥梁健康监测系统应用的传感器类型复杂且数量较多,造成系统难以分析与监测数据无关的冗余信息。不过,长大桥梁健康监测系统中时序冗余效应突出,例如主梁不同截面位置上响应数据的相似性、相关性以及斜拉索上面内与面外加速度数据的相关性等[2]。
为了充分利用监测数据的冗余性实现监测系统的自诊断,需要对监测数据的冗余信息进行相关性分析。然而,传统相关性分析方法尚无法有效消除监测数据中通常存在的时滞对相关性指标带来的不利影响。数据时滞的表现特征是两组同类型传感器所测数据的时域波形相似,但监测数据对应的时刻点不同;其产生原因通常如下:不同传感器测到的数据往往由不同的数据采集卡记录,所以这些数据通常不能在同一时间进行采集,从而不同传感器测到的数据之间存在时滞[3,4]。
为此,针对数据时滞的数据异常情况,研究一种基于数据关联度的数据异常识别方法,进行监测系统的自诊断。首先介绍了关联度分析的基本理论;再以应变、加速度、位移等实测数据为例,验证灰色关联度指标对实测数据时滞的鲁棒性[5]。
1 关联度理论
首先,灰色系统是一种相对于白色系统和黑色系统的非确知信息的系统,这种系统同时包含已知信息和未知信息。灰色关联度分析是一种多因素的统计分析方法,它依据序化分析与关联测度量化不同层次中多个序列相对某一级别的关联性。灰色关联度分析的基本思想是假设已知某一个指标可能是与其他的某几个因素相关的,寻求这个指标与其他哪个因素相对来说更有关系,而哪个因素相对关系弱一点,依次类推,把这些因素排个序,得到一个分析结果,就可以知道关注的这个指标,与哪些因素更相关[6]。
对于多个时序数据,若其中两个变化趋势具有一致性,且具有时间同步变化特征,二者的关联度就较高;反之则较低。灰色关联分析是根据序列曲线几何形状的相似程度来判断其联系是否紧密,可以把握系统各个因素间时间趋势相关性的大小[7]。因此,灰色关联度分析对于系统的时间发展态势可进行量化,适用于动态历程系统的分析。
1.1 关联的度量
长大桥监测系统的关联性表现在监测系统与外界环境、荷载作用的相互作用,可以分为环境关联性、结构关联性、位置关联性、时间关联性、类别关联性等几类。传感器输出的数据都是结构在外部作用下的响应输出。按不同测点数据趋势的方向可以将传感器间的关联性分为无相关、正相关和负相关。
系统灰色关联度分析模型
R=E×W
(1)
式中:R为m个被评价对象的综合评价结果向量;W为n个评价指标的权重向量;E为各指标的评判矩阵。根据R的数值,进行排序。具体步骤如下。
(1)确定最优指标集。
设
(2)
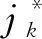
(2)指标的规范化处理。
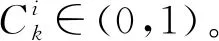
(3)
(3)计算综合评判结果。
(4)
式中:ρ∈(0,1),一般取ρ=0.5。
这样综合评价结果参考式(1),若关联度Ri最大,说明C与最优指标C*最接近,即第i个被评价对象优于其他被评价对象,据此可以排出各被评价对象的优劣次序。
1.2 关联度分析步骤
(1)首先确定反映系统特征行为的参考数列以及影响系统行为的比较数列。
(2)然后对所有参考数列和比较数列进行数据标准化的无量纲化处理。
设有序列
x=(x(1),x(2),…,x(n))
(5)
称映射
f:x→yf(x(k))=y(k),k=1,2,…,n
(6)
为序列x到序列y的数据变换。
进行数据标准化变换的数据变换包括初值化变换、均值化变换、百分比变换、倍数变换、极差最大化变换、区间值化变换等方法。
(3)求解关联系数ξ(Xi)。
依据式(4)可计算出关联系数ξ(Xi),作为各因素在各个时刻的关键程度指标。
(4)求关联度ri。
由于关联系数包含了各个时刻的相关程度值,所以它是随数据长度不同而不同的多个指标,造成信息过于分散,难以直接比较。因此对其进行平均处理,作为比较数列与参考数列间关联程度的量ri。
(5)排关联序。
从小到大将m个子序列对同一母序列的关联度进行排列,组成关联序{x},表示对母序列来说各子序列的“优劣”关系。若r0i>r0j,则称{xi}对于同一母序列{xi}优于{xj},记为{xi}>{xj};其中r0i、r0j分别代表参考数列、比较数列的特征值。
2 应用实例
采用江阴大桥的应变、加速度、位移等实测数据作为算例,利用同一传感器所测数据来构造具有时滞的相同数量的两组数据,以此考察灰色关联度分析方法对实测信号时滞的鲁棒性。
2.1 应变数据
江阴长江大桥共布设了80个应变传感器,分布于9个截面上。每个截面8个测点,光纤应变传感器布设在箱梁内部,传感器布局如图1所示。
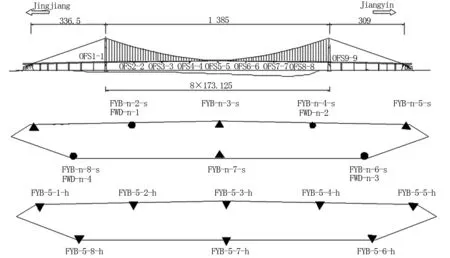
图1 光纤应变传感器的布局
采用2009年11月8日的应力数据为例,采样频率为1 Hz,以截面1上2号传感器所测数据构造5、10、15 min时滞的三组数据。以5 min为单位分别对287、286、285组测试数据进行相关性分析的计算结果见图2(a),由图2(a)所示关联度给出所对应概率密度如图2(b)所示。

图2 2009年11月8日截面1上应变数据的时滞对灰色关联度的影响
观察图2可知:虽然灰色关联度分析方法对实测应变数据时滞不如对仿真信号时滞的鲁棒性好,但在时滞为5、10、15 min的情况下,灰色关联度仍然较为集中地分布在0.68附近,其标准差在0.01左右;采用江阴大桥截面1上2号传感器所测2009年1月份每天的应变数据构造时滞为1 min的数据,以1 min为单位对计算得到的灰色关联度指标进行统计,可知:截面1上2号传感器所测数据的灰色关联度均值为0.613,标准差为0.008 3,与图相比没有明显不同。因此,综合计算结果与统计资料,得出如下结论:灰色关联度分析方法对实测应变数据的时滞具有较好的鲁棒性。
2.2 吊杆加速度数据
这里以吊杆上加速度传感器为例进行说明。
基于2009年12月30日的3号截面上传感器所测加速度数据,数据采样频率为50 Hz,以传感器AH3NEL所测数据构造5、10、15 min时滞的三组数据,以1 min为单位分别对1 439、1 438、1 437组测试数据进行相关性分析的计算结果见图3(a),由图3(a)所示关联度给出所对应概率密度如图3(b)所示。
观察图3可知:虽然灰色关联度分析方法对实测加速度数据时滞不如对仿真信号时滞的鲁棒性好,但在时滞为5、10、15 min的情况下,灰色关联度仍然较为集中地分布在0.67附近,其标准差是0.008;采用江阴大桥吊杆加速度传感器AH3NEL所测2009年1月份每天的加速度数据构造时滞为1 min的数据,以1 min为单位对计算得到的灰色关联度指标进行统计,可知:传感器AH3NEL所测数据的灰色关联度均值为0.631,标准差为0.0068,与图相比没有明显不同。因此,由综合计算结果与统计资料得出如下结论:灰色关联度分析方法对实测加速度数据的时滞具有较好的鲁棒性。
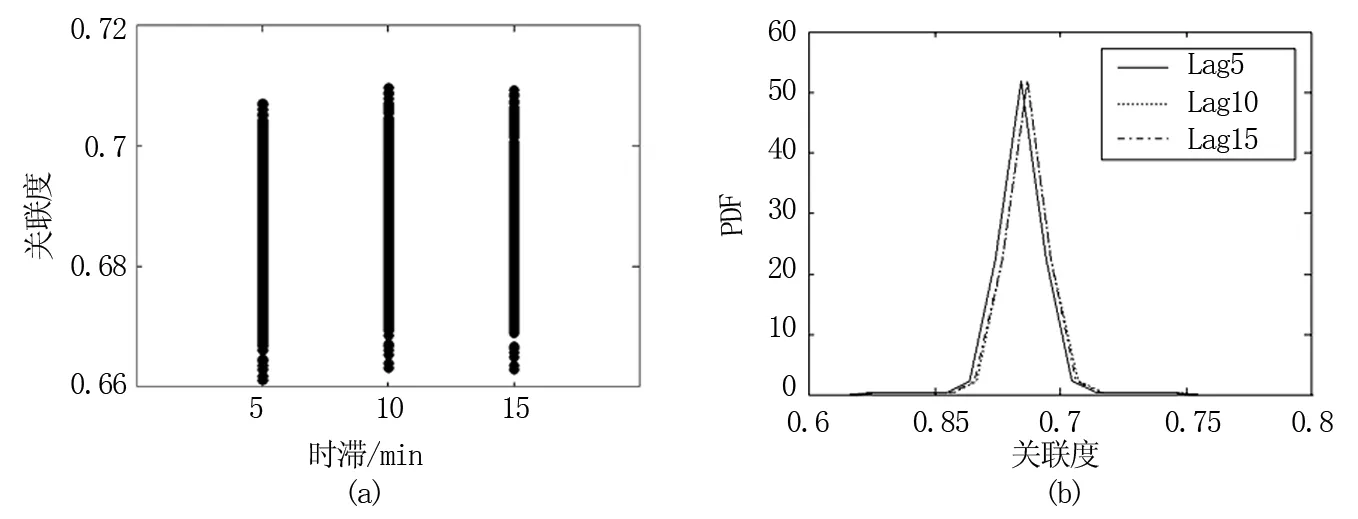
图3 2009年12月30日吊杆上加速度数据时滞对灰色关联度的影响
2.3 梁端位移数据
基于2009年3月19日的位移传感器所测数据,数据采样频率为50 Hz,采用传感器WYJ3NE所测数据构造5、10、15 min时滞的三组数据,以1 min为单位分别对1 439、1 438、1 437组测试数据进行相关性分析的计算结果见图4(a),由图4(a)所示关联度给出所对应概率密度如图4(b)所示。

图4 2009年3月19日梁端位移数据时滞对灰色关联度的影响
由图4可知:虽然灰色关联度分析方法对实测位移数据时滞不如对仿真信号时滞的鲁棒性好,但在时滞为5、10、15 min的情况下,灰色关联度仍然分别较为集中地分布在0.57附近,其标准差为0.009;采用江阴大桥梁端位移传感器WYJ3NE所测2009年1月份每天的位移数据构造时滞为1 min的数据,以1 min为单位对计算得到的灰色关联度指标进行统计,可知:WYJ3NE所测数据的灰色关联度均值为0.523,标准差为0.007 8,与图相比没有明显不同。因此,由综合计算结果与统计资料得出如下结论:灰色关联度分析方法对实测梁端位移数据的时滞具有较好的鲁棒性。
3 结 论
(1)灰色关联度分析方法是数据相关性的有效分析方法,适用于计算具有时滞特征的长大桥梁应变、加速度和位移数据的相关性分析。
(2)采用灰色关联度分析方法对存在时滞的江阴大桥的实测应变、加速度、位移数据进行关联度计算,结果表明虽然灰色关联度分析方法对实测数据时滞不如对仿真信号时滞的鲁棒性好,但在时滞为5、10、15 min的情况下,灰色关联度仍然分别较为集中地分布在0.55~0.75之间,其标准差在0.01~0.05之间;与根据相应传感器所测2009年1月份每天的实测数据得到的灰色关联度指标的统计结果相比没有明显不同。因此,灰色关联度分析方法对实测应变、加速度、位移数据的时滞具有较好的鲁棒性,从而验证了灰色关联度分析方法对实测数据的时滞具有较好的鲁棒性。
