两类正则图的邻点全和可区别全染色
2022-04-15常景智杨超程银万王芹姚兵
常景智,杨超,程银万,王芹,姚兵
1.上海工程技术大学 数理与统计学院 智能计算与应用统计研究中心,上海 201620;2.西北师范大学 数学与统计学院,兰州 730070
图的可区别染色问题是图论中的经典问题之一,随着可区别染色问题被广泛应用于计算机科学、生物学以及网络安全等领域,这一问题被越来越多的国内外学者所研究.近年来,关于把点和边所染颜色相加的可区别染色问题引起了人们的极大关注.文献[1]介绍和研究了图的邻和可区别边染色,并提出下述著名的1-2-3猜想:
猜想1[1](1-2-3猜想) 设G为一个阶数至少为3的简单连通图,则gndiΣ(G)≤3.
文献[2]证明了阶数至少为3的简单连通图的邻和可区别边色数不超过5.关于邻和可区别边染色的相关研究见文献[3-6].文献[7]提出了图的邻和可区别全染色的概念,并给出了此定义下的1-2猜想:
猜想2[7](1-2猜想) 设G为一个简单连通图,则tgndiΣ(G)≤2.
文献[8]得到了任意图的邻和可区别全色数不超过3.文献[9]考虑把任意点的关联边与其邻点所染颜色相加,定义了图的邻点被扩展和可区别全染色,且得到了一些特殊图的邻点被拓展和可区别全色数.文献[10]研究了仙人掌图的邻点被拓展和可区别全染色.不仅如此,文献[9]又在邻点被扩展和可区别全染色的基础上考虑加上点本身的颜色,介绍了下述关于图的一类新染色——邻点全和可区别全染色:

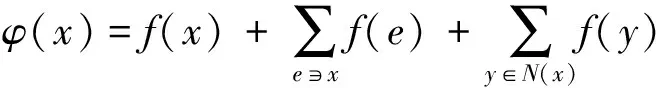
其中
N(x)={y∈V(G)|xy∈E(G)}
对任意的边uv∈E(G),如果有φ(u)≠φ(v)成立,则称f是图G的一个邻点全和可区别(简记NFSD)k-全染色.图G的邻点全和可区别全染色中最小的k值称为G的邻点全和可区别全色数,记为fgndiΣ(G).
本文研究了广义Petersen图和循环图的邻点全和可区别全染色问题,确定了它们的邻点全和可区别全色数.文中涉及的染色均为非正常的,不失一般性,约定下文证明过程中凡是未被染色的点和边均染颜色1.
1 广义Petersen图

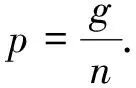
定理1当n为偶数,k为奇数时,fgndiΣ(P(n,k))=2; 其他情形时,fgndiΣ(P(n,k))≤3.
由定义2知P(n,k)是一类三正则图,则fgndiΣ(P(n,k))≥2.定理1分以下3个引理证明:
引理1当n为偶数,k为奇数时,fgndiΣ(P(n,k))=2.
证定义P(n,k)的一个2-全染色f:f(aiai+1)=f(aibi)=f(aibi+k)=1,f(ai)=2(i为奇数),f(bi)=2(i为偶数).由染色f可得P(n,k)中各点的权重为:φ(ai)=10(i为奇数),φ(ai)=8(i为偶数),φ(bi)=8(i为奇数),φ(bi)=10(i为偶数).因bi总与bi+k相连,所以内圈中的相邻点下标的奇偶性不同,则有φ(bi)=10(i为偶数)≠φ(bi)=8(i为奇数),证毕.
引理2当n为偶数,k为偶数时,fgndiΣ(P(n,k))≤3.
证根据不交圈的长度p,分以下3种情形讨论:


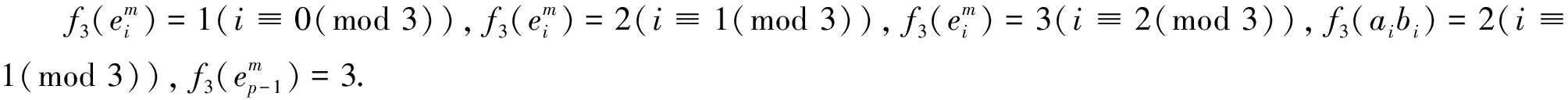
引理3当n为奇数时,fgndiΣ(P(n,k))≤3.
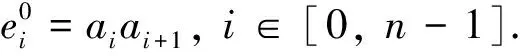
情况2 对内圈染色:令f(ai)=1,f(bi)=3.当p≢2(mod 3)时,令当p≡2(mod 3)时,令
2 循环图
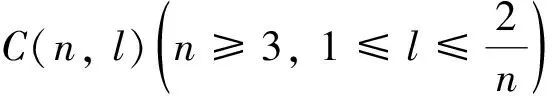

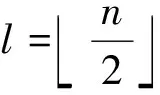
由定义3知C(n,l)是正则图,则fgndiΣ(C(n,l))≥2.定理2分以下4个引理证明:
引理4当n为偶数,l为奇数时,fgndiΣ(C(n,l))=2.
证定义C(n,l)的一个2-全染色f如下:f(aiai+1)=f(aiai+l)=1,f(ai)=2(i≡1(mod 2)).由染色f可得C(n,l)中各点的权重为:φ(ai)=10(i≡0(mod 2)),φ(ai)=13(i≡1(mod 2)),证毕.
引理5当n为奇数,l为偶数时,fgndiΣ(C(n,l))≤3.
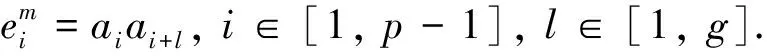
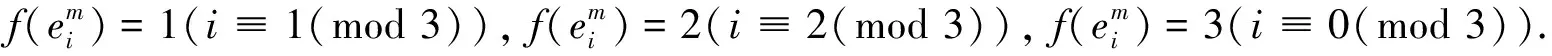
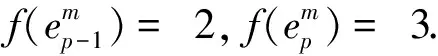
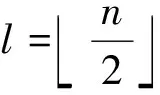
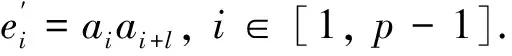

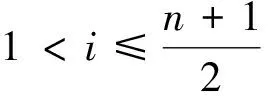
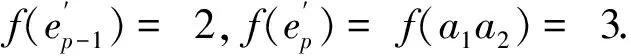
引理7当n=2l时,fgndiΣ(C(n,l))=2.



情形2 当l=3时,令f(a1a4)=f(a3a4)=f(a4a5)=f(a4)=2,得φ(a1)=φ(a3)=φ(a5)=9,φ(a2)=φ(a6)=7,φ(a4)=11.
情形3 当l=4时,令f(a1a5)=f(a3a7)=f(a3a4)=f(a4a5)=f(a5a6)=f(a5)=2,得φ(a1)=φ(a3)=φ(a6)=9,φ(a2)=φ(a8)=7,φ(a4)=10,φ(a5)=11,φ(a7)=8.
情形4 当l=5时,令f(a1a6)=f(a3a8)=f(a4a9)=f(a2a3)=f(a5a6)=f(a6a7)=f(a9a10)=f(a4)=2,得φ(ai)=9(i=1,3,5,7,9),φ(a2)=φ(a4)=φ(a8)=φ(a10)=8,φ(a6)=11.
