中学生数学学习投入与内在动机的关系：一项纵向研究

2022-04-15张勇强杨新荣

西南大学学报（自然科学版） 2022年4期

张勇强，杨新荣，2

1.西南大学教师教育学院，重庆 400715； 2.中国基础教育质量监测协同创新中心西南大学分中心，重庆 400715

长期以来，学生认知因素的培养是基础教育研究者关注的热点．而随着基础教育质量评估范式的转型和教育质量观的嬗变，目前，国际上对中学人才培养质量的关注不再局限于认知因素，而转向于学生学习获得感、学习过程[1-2]．学生学习投入作为与中学生学习收获、学习过程直接相关的关键因素，正日益成为国际教育研究者关注的焦点[3-4]．在数学学习上，研究表明学生学习投入得越多，不仅可以收获更好的学业成绩，也可以促进其身心健康的发展[5]．近年来，大量的实证研究也都表明数学学习投入对中学生学业成就、课堂表现、学习能力、个人发展等都有积极的影响[6-7]．不过调查发现，中学生数学学习投入水平在持续地呈下降趋势[8]．因此，系统探索中学生数学学习投入的影响因素，理清相关变量与数学学习投入间的相互作用，对于提升中学人才培养质量和数学教学质量具有重要的教育价值．

数学学习投入是指学生在数学学习活动过程中表现出对学习的一种持续的、充满积极情感的状态，主要包括数学认知、行为和情感投入等3个维度[9]．这些维度既相互影响，又相互独立．已有研究表明数学学习投入不仅受先赋性因素如性别和家庭环境等的影响[10]，也受到教育性因素如学习经验、课堂环境、学习兴趣、师生互动、同伴合作、学习机会等的影响[5，11-13]．近年来，众多研究发现除先赋性因素和教育性因素外，学生个性心理方面也是学习投入的主要影响因素．在个性心理特征方面，研究者普遍认为学习动机是学习投入的基础，也是学生学习行为的重要前提[14]．已有研究发现学习动机是影响学习投入的重要预测变量，不同类型的学习动机对学习投入有着不同的影响[15-16]．在Deci和Ryan的自我决定动机理论框架中，研究者依据行为产生的不同目标和原因，将学生的动机分为内在动机、外在动机和无动机等3种类型，其中最为基础的是内在动机和外在动机[17]．研究发现相较于外在动机，内在动机驱动的数学学习行为更加持久、表现更好，更有助于激发学生进行积极的、有策略的和高质量的学习活动，同时也能够培养学生的创新能力[18]．

对于学习动机与学习投入的关系，研究者普遍重视学习投入与内在动机的关系研究．内在动机是指个体为了满足个人兴趣、发展能力、好奇心、自尊等自我内发性精神需要所引发的一种伴有积极情绪体验的行为倾向[19]．研究表明，内在动机是学生进行学习行为与取得学业成就的动力源泉，是学习投入的积极预测因素[17]．若学生保持高水平的内部动机进行学习任务时，会在一定程度上表现出更高的投入水平和更好的表现．近年来，研究发现内在动机对不同类型的学习投入有着不同的影响，可以被认为是认知、行为和情感投入的重要推动力量．受内在动机激励的学生，他们在面对学习困难时会更加坚持、乐观和自信，也愿意花费更多的时间参与学习活动，最终通过吸收、分析、整合和理解学习内容提升自身认知策略，进而保持较高水平的认知、行为和情感投入[16，20]．多项实证研究也证明，内在动机不仅可以正向预测学习过程中的认知投入、行为投入和情感投入，还可以通过对学习投入的作用间接地影响学生的学业表现[15-16，21]．

另一方面，学习投入也是学生内在动机获得的重要影响变量．研究发现当学生积极付出更多的努力和投入而能够取得较好的学习结果时，他们的内在学习动机会得到进一步的提升．此外，实证研究也都表明学习投入对学生内在动机的发展具有显著的正向促进作用[22]．近年来，开始有研究者从学习投入的不同维度出发，探讨不同类型的投入对内在动机的影响和预测作用[16，18]．研究发现，情感投入的学生会对课堂任务更感兴趣和好奇，进而激发学生对获取知识的渴望，提升自身学习的内在动机水平．行为投入的学生会积极参与学习活动，并会在活动的过程中发展其个人兴趣和能力，提升个人内在动机水平．认知投入的学生更注重对学习内容的理解，表现出强烈的好奇心和求知心态，会在一定程度上促进内在动机的发展．此外，行为和情感投入也可以预测下一时间点的内在动机水平．

综上所述，虽然先前很多研究探讨了内在动机与认知、行为和情感投入的关系，但是仍存在一些局限．首先，以往研究主要关注非学科背景下两者的关系，还鲜有研究在数学背景下对内在动机与认知、行为和情感投入的关系进行探讨；其次，以往研究主要是横断研究，对二者的关系研究大多是单向预测，缺乏对两者相互预测关系的研究．基于此，本研究采用纵向数据和交叉滞后模型设计，探讨中学生内在动机与数学认知、行为和情感投入的相互预测关系，并作出如下初步假设：① 中学生的内在动机可以显著正向预测其数学认知、行为和情感投入； ② 中学生的数学认知、行为和情感投入可以显著正向预测其内在动机．

1 研究方法

1.1 研究对象

本研究采用整群抽样法选取重庆市、贵阳市和济南市的3所中学的初二年级和高二年级的学生为追踪调查对象，对其进行为期一年半共3个时间点的追踪调查．第一次调查是在2019年12月(T1)，第二次调查是在2020年12月(T2)，第三次调查是在2021年5月(T3)．3次调查结束后，删除3次调查中缺失、不认真作答及信息不一致等调查问卷，最终保留3次调查信息一致的参与者，共获得有效被试365人，其中初中生170人，高中生195人；男生172人(47.1%)，女生193人(52.9%)；城市学生281人，农村学生84人．

1.2 研究工具

1.2.1 数学学习投入问卷

采用Fredricks等人编制的数学学习投入问卷评估学生的数学学习投入[23]．该量表包含认知投入(9个项目)、行为投入(11个项目)、情感投入(11个项目)以及社会投入(7个项目)4个分量表，共38个项目．各分量表中所有项目采用Likert 5点计分(1=完全不同意，5=完全同意)，分数越高，表明数学学习投入水平越高．在本研究中，选取认知投入(如我会仔细检查所完成的数学功课来确保它们的准确性)、行为投入(如在数学课上，我会聚精会神地听讲)和情感投入(如我经常在数学学习上感到很有挫败感)3个分量表作为本次研究的调查工具．经项目分析和因素分析后，删除相关性不显著和因子载荷量较小的题项，最终数学学习投入问卷共保留13个项目，其中认知投入保留4个项目，行为投入保留3个项目，情感投入保留6个项目．在3次测量中，认知投入量表的Cronbach’sα系数分别为0.76(T1)，0.79(T2)，0.70(T3)；行为投入量表Cronbach’sα系数分别为0.77(T1)，0.79(T2)，0.77(T3)；情感投入量表Cronbach’sα系数分别为0.87(T1)，0.89(T2)，0.69(T3)．

1.2.2 内在动机问卷

采用Pintrich等编制的学习动机策略问卷(Motivated Strategies for Learning Questionnaire，MSLQ)评估学生的内在学习动机[24]．内在动机问卷中所有项目均由第一作者翻译成中文，并由具有良好中英文知识的数学教育研究员进一步检查，同时邀请两位经验丰富的中学数学老师检查所有项目的内容．该问卷在中国背景下得到有效验证，目前在中国被广泛用于调查学生的内在动机，包括数学学习的内在动机．修改后的中文版内在动机问卷包括7个项目(如理解数学对我而言很重要)．经项目分析和因素分析后，删除相关性不显著和因子载荷量较小的题项，最终内在动机问卷共保留4个项目．在3次调查中，内在动机问卷的Cronbach’s α系数分别为0.75(T1)，0.78(T2)，0.79(T3)．

1.3 数据处理

所有回收问卷在统一指导下进行团体整理与编码．使用SPSS 26.0和Mplus 8.0软件对收集的数据进行录入与分析．首先使用SPSS 26.0对整理后的数据进行项目分析和因素分析，然后对已处理的数据进行共同方法偏差检验，接着采用描述性统计考察中学生数学学习投入与内在动机在时间上的变化、采用单因素重复测量方差探究数学学习投入与内在动机的稳定性、采用相关分析考察数学学习投入与内在动机间的横向和纵向关系，最后使用Mplus 8.0数据处理软件对中学生内在动机与数学认知、行为和情感投入之间的相互预测关系分别进行交叉滞后模型分析．

2 研究结果

2.1 共同方法偏差的检验

由于数学学习投入和内在动机的调查数据均来自中学生的自我报告，因此本研究调查数据可能存在共同方法偏差．采用Harman单因素检验，因素分析结果显示，在未旋转的情况下分别得到4个因子，3次测量中最大因子的解释量为38.738%，小于40%的临界点[25]，故而认为本研究调查数据不存在明显的共同方法偏差．

2.2 数学学习投入与内在动机的描述统计及相关分析

表1 数学认知投入、行为投入、情感投入和内在动机的描述性统计

2.3 数学学习投入与内在动机的相关分析

中学生数学学习投入与内在动机的相关分析如表2所示．首先，相关分析结果表明，无论是在T1～T3时间点的同时性相关，还是在T1～T3时间点的继时性相关，内在动机与数学认知、行为和情感投入间的相关性都达到显著水平，相关系数在0.191～0.695之间．其次，内在动机与数学认知、行为和情感投入在相同时间点的相关性强于在不同时间点的相关性，相关系数在0.362～0.695之间．最后，通过比较发现，在T1～T3时间段，内在动机与数学情感投入的相关性强于内在动机与数学认知和行为投入的相关性，相关系数在0.212～0.695之间．这些差异表明，内在动机与数学情感投入间的关系比内在动机与数学认知和行为投入的关系更为密切．

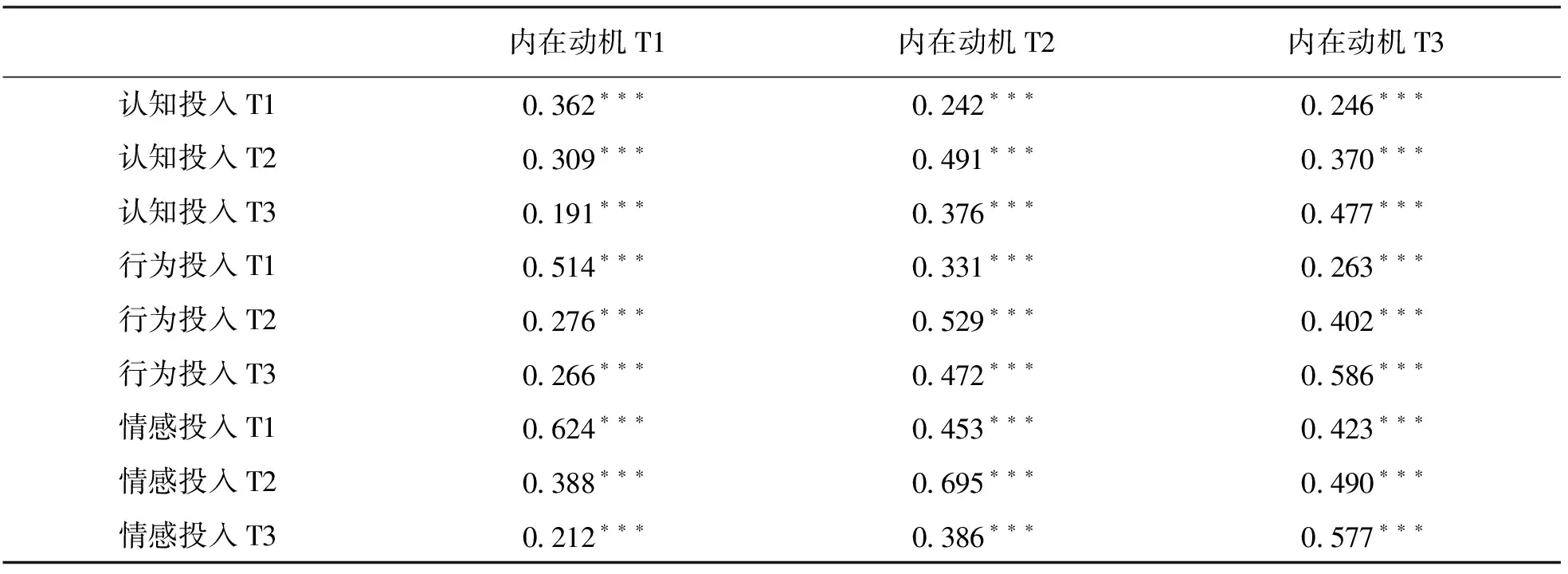
表2 数学认知投入、行为投入、情感投入和内在动机的相关分析

2.4 数学学习投入与内在动机的交叉滞后分析

本研究采用交叉滞后路径分析来检验中学生内在动机与数学认知、行为和情感投入之间的相互预测关系．首先，在Mplus 8.0中估计了内在动机与数学认知、行为和情感投入之间的稳定性系数．其次，关联了T1，T2和T3时间点内在动机与数学认知、行为和情感投入之间的残差相关．最后运用Mplus 8.0分析软件考察了各模型的拟和情况．

图1展示了中学生内在动机与数学认知投入之间的交叉滞后分析模型结果．分析结果显示，模型拟合指数良好：χ2/df=3.20，RMSEA(90%CI)=0.078(0.032～0.127)，CFI=0.985，TLI=0.947，SRMR=0.027．从路径分析发现，前测的内在动机均能显著正向预测随后时间点的数学认知投入，路径系数均为0.169(p<0.01)，说明中学生的内在动机越高，随后的数学认知投入就更多．而前测时间点的数学认知投入对随后时间点的内在动机预测作用不显著，路径系数分别为0.097，0.083(p>0.05)，表明中学生数学认知投入水平不能预测随后时间点的内在动机．

*** p<0.001； ** p<0.01； * p<0.05．图1 中学生数学认知投入与内在动机的交叉滞后模型

图2展示了中学生内在动机与数学行为投入之间的交叉滞后分析模型结果．分析结果发现，模型拟合指数良好：χ2/df=2.75，RMSEA(90%CI)=0.069(0.021～0.120)，CFI=0.989，TLI=0.960，SRMR=0.027．路径系数显示，中学生的内在动机在T1和T2时间点均能显著正向预测随后时间点的数学行为投入，路径系数分别为0.120(p<0.05)和0.274(p<0.01)，说明中学生内在动机越高，随后的数学行为投入也会更多．同时随着时间的推移，内在动机对数学行为投入的预测作用也在增强．此外，前测时间点的数学行为投入也均可显著正向预测随后时间点的内在动机，路径系数分别为0.154(p<0.01)和0.100(p<0.05)，说明中学生数学行为投入越多，随后的内在动机也会更强．但随着时间的推移，数学行为投入对内在动机的预测作用在减弱．

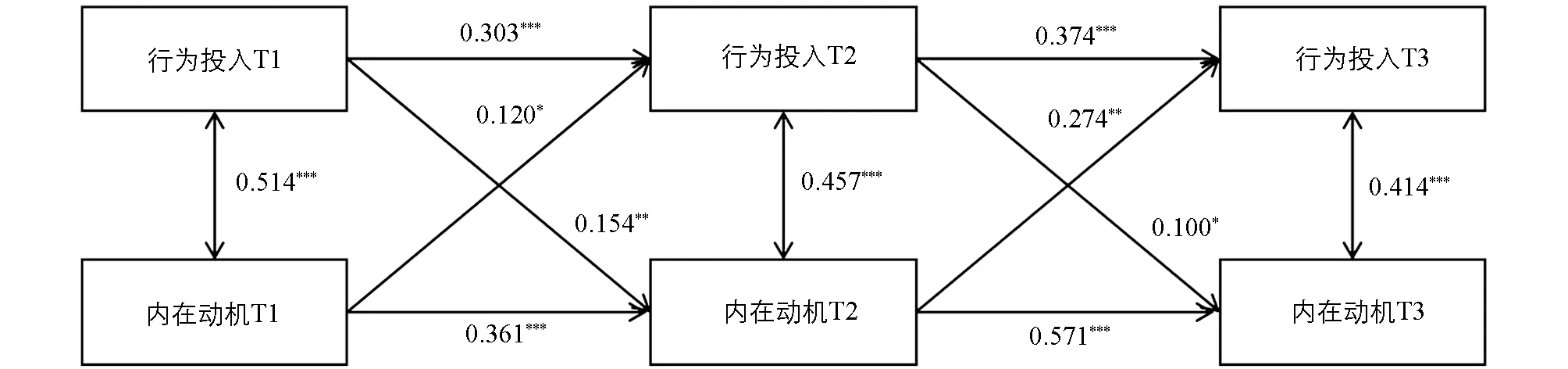
*** p<0.001； ** p<0.01； * p<0.05．图2 中学生数学行为投入与内在动机的交叉滞后模型

图3展示了中学生内在动机与数学情感投入之间的交叉滞后分析模型结果．分析结果发现，模型拟合指数良好：χ2/df=3.20，RMSEA(90%CI)=0.078(0.032～0.127)，CFI=0.988，TLI=0.960，SRMR=0.030．路径系数显示，前测时间点的数学情感投入均能显著预测随后时间点的内在动机，路径系数分别为0.296(p<0.001)和0.110(p<0.05)，说明中学生数学情感投入越多，随后的内在动机就更强．但随着时间的发展，数学情感投入对内在动机的预测作用在减弱．此外，内在动机仅在T2时间点能够显著预测随后时间点的数学情感投入，路径系数为0.229(p<0.001)，说明在T2～T3时间段，内在动机越高，随后的数学情感投入就更多．

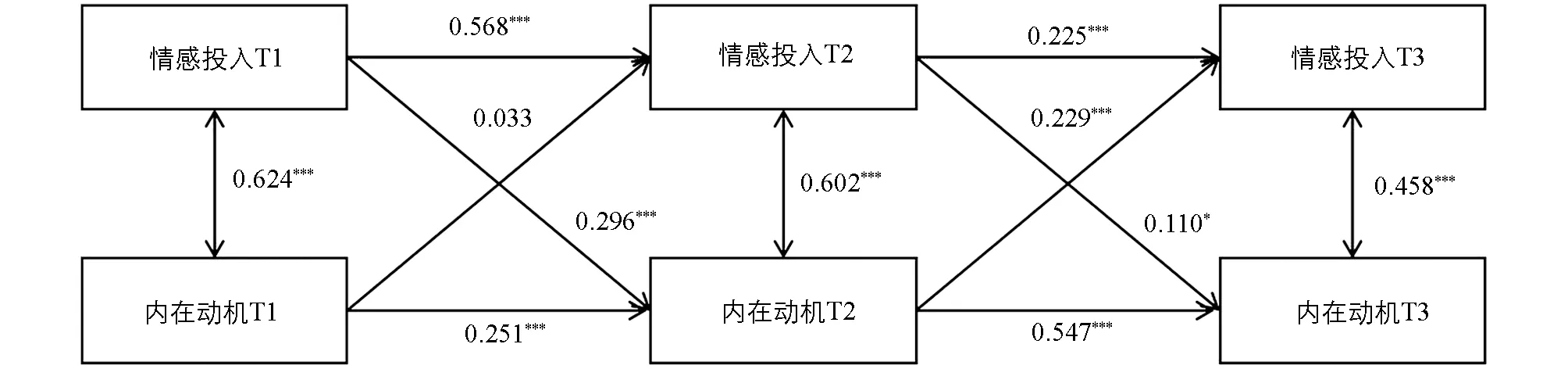
*** p<0.001； ** p<0.01； * p<0.05．图3 中学生数学情感投入与内在动机的交叉滞后模型

3 讨论

3.1 中学生内在动机与数学认知、行为和情感投入的发展状况及稳定性

另外，中学生内在动机与数学认知、行为和情感投入分别在T1，T2和T3时间点间的相关性较高，相关系数在0.362～0.695之间．这表明中学生的内在动机和数学学习投入表现出一定程度跨时间的稳定性，这与以往针对小学生数学学习投入和高中生内在动机的研究结果一致[20，28]．内在动机是一种在活动过程中所引发的伴有积极情绪体验的行为倾向，导致个体内在动机变化的因素有很多，如外在环境、个体需要、兴趣、情感因素、成就目标以及激励与反馈等[19]．此外，除外在因素的改变有可能在短时间内进行调整外，而其他内在因素的改变都需要比较长的时间，因此，中学生内在动机的变化在T1，T2和T3时间点呈现出一定的稳定性．由于学习投入是一种与学习相关的、持久的、积极的行为倾向，包括情感、行为和认知投入3个维度，同时在短时间内也具有一定的可塑性，所以数学认知、情感和行为投入在T1，T2和T3时间点也表现出相对的稳定性．

3.2 中学生内在动机与数学认知投入间的相互预测关系

中学生内在动机和数学认知投入的交叉滞后分析结果表明，在T1到T3时间段上，前一时间点的内在动机水平均能够显著正向预测个体后一个测量时间点的数学认知投入(β=0.169，p<0.01)，这表明中学生内在动机水平越高，其数学认知投入水平就越高，前面学者的研究也发现内在动机是中学生认知投入的重要预测变量[21]．中学生保持积极的内在学习动机可以促使其追求更加具有挑战性的数学学习任务，进而促使学生进行自我管理、反思以及获取解决问题的策略等[29]．先前研究也表明，内在动机可以加强学生对学习任务的感知，即感知学习任务的重要性、学习内容的有趣性以及学习知识的有用性等，而内在动机水平越高的学生，更容易在感知的过程中保持较高的认知和元认知策略的使用[29]．此外，当学生拥有较多积极的内部因素时，如学习情绪、自我效能感、信念等，会促进其内在动机的发展，这使得学生在应对遇到的困难和挑战时更能激发其学习策略并寻求相应的方法与策略解决问题，从而使得认知投入得到强化[30]．

另外，交叉滞后结果显示，在T1和T2时间点上的数学认知投入水平分别不能显著预测T2和T3时间点上的内在动机水平(β=0.097，β=0.083，p>0.05)，这意味着随着认知投入程度的增加，中学生内在动机水平没有显著增强，与我们的原假设不符．这可能与影响内在动机的因素和中学生这一群体有关．数学认知投入并不是导致中学生内在动机的唯一因素，研究显示，学生的自我效能感、成就目标、兴趣等心理变量也是诱发中学生内在动机的重要因素[31]，且中学生随着年级的增加，数学学习内容难度加深，学习负担日益加重，同时也承受着中、高考的竞争压力，导致中学生的内在动机被消弱[31]．这些都在一定程度上降低了数学认知投入对中学生内在动机的影响，进而导致数学认知投入并不一定直接影响其内在动机．

3.3 中学生内在动机与数学行为投入间的相互预测关系

中学生内在动机和数学行为投入的交叉滞后分析结果显示，T1时间点的内在动机显著正向预测T2时间点的数学行为投入(β=0.120，p<0.05)，且预测强度弱于T2时间点的内在动机正向预测T3时间点的数学行为投入的强度(β=0.274，p<0.01)，这表明中学生内在动机水平越高，数学行为投入水平就越高．同时，随着时间的推移，内在动机对数学行为投入的预测强度在增强．这一结果符合前人的研究结果，即个体的内在动机水平能够显著预测其行为投入的程度[32]．内在动机为持续的行为投入提供了燃料，内在动机水平越高的学生，其较强的认知需求对个体探究和求证的行为产生驱动力，且求知欲在很大程度上是出于个体的内在动机，内在动机不仅可以提升个体的行为投入，更能使个体在学习过程中产生沉浸状态，体现出较高的行为投入．也有研究发现，受内在动机驱动的学生，当他们面对学习挑战时，可能在学习活动中表现得更加持久、努力和专注，进而加强学生学习行为上的参与[21]．

此外，T1时间点的数学行为投入显著正向预测T2时间点的内在动机(β=0.154，p<0.01)，且预测强度强于T2时间点的数学行为投入正向预测T3时间点的内在动机的强度(β=0.100，p<0.05)．结果表明，数学行为投入水平高的学生内在动机水平也更高，但随着时间的推移，数学行为投入对内在动机的预测强度在减弱．这与先前研究者把内在动机作为情感投入，并发现行为投入对情感投入具有预测作用的结果是一致的[32-33]．中学生参与数学活动的强度和努力程度越高，越能积极地完成数学课堂活动和老师布置的数学任务，这些都有助于中学生在数学活动中表现得更好，同时在数学测试中获得更高的成就，从而促进其内在学习动机水平的提升[5，31]．

3.4 中学生内在动机与数学情感投入间的相互预测关系

中学生内在动机和数学情感投入的交叉滞后分析结果显示，数学情感投入分别显著正向预测T2和T3时间点的内在动机，且T2时间点的数学情感投入对T3时间点的内在动机的预测强度(β=0.110，p<0.05)弱于T1时间点的数学情感投入对T2时间点的内在动机的预测强度(β=0.296，p<0.001)，这表明中学生的情感投入水平越高，内在动机水平就越高，同时随着时间的推移，数学情感投入对内在动机的预测强度在减弱[18]．认知-动机理论认为，在学习过程中，情感具有动力性，可以激发并维持个体内在学习动机，使其学习活动得以保持下去[30]．除此之外，当学生在学习活动中有较高的情感投入时，他们表现得就更加积极主动，并在活动中伴有较多的情感体验，如乐趣、好奇心等，他们就更愿意主动参与学习和积极地完成学习任务，其内在动机水平就越高[19]．

另外，T2时间点的内在动机显著正向预测T3时间点的数学情感投入(β=0.229，p<0.001)，但T1时间点的内在动机不能预测T2时间点的数学情感投入(β=0.033，p>0.05)，这在一定程度上反映出内在动机对数学情感投入的预测是不稳定的．在T1到T2 时间段，中学生的内在动机不能预测其数学情感投入，这可能是由于高水平内在动机的学生也保持着较高的外在动机水平，学生的学习动机和学习态度由单纯的兴趣和好奇心变得具有一定的功利性和目的性，因此阻碍了学生的情感投入过程[34]．此外，早期的数学认知和行为投入均受到内在动机的正向影响，这也对后期中学生的内在动机对其数学情感投入的预测起到促进作用．积极的数学行为和认知投入会加强学生的学习强度和学习效率，可能促进其进行有意义的情感投入在数学中，这也就导致了T2到T3时间段内在动机对数学情感投入的预测作用[20]．