基于GAN 网络的时间序列预测算法

2022-04-15闫保中苏邓军

应用科技 2022年2期

闫保中，苏邓军

哈尔滨工程大学智能科学与工程学院，黑龙江哈尔滨 150001

通过挖掘多维时间序列相互之间的结构关系以及时间序列中反映出的变量随时间不断变化的趋势，利用历史数据对未来的数据进行预测，在商业和工业领域有着重要的意义[1-4]。如预测电力负荷数据，从而对发电量等资源的配置进行优化[5-6]。传统的时间序列预测模型，如差分自回归移动平均模型(autoregressive integrated moving average model，ARIMA)、指数平滑等，主要利用较为单一的数据特征，如数据的周期性、变化趋势等进行预测，对于单一的自回归序列，该类算法具有较好的预测效果，但由于其无法捕捉序列自身或序列复杂的结构关系，对于较复杂的多维时间序列等，该类算法不能获得较好的预测效果。随着深度学习技术的发展，国内外学者基于深度学习技术对时间序列预测开展了更深入的研究，如基于循环神经网络的编码器模型[7-8]以及注意力模型[9]。Qin 等[7]模仿人类注意力机制提出了一种双阶段注意力机制的自编码网络，解决了传统网络对多维时间序列无法捕捉较长时间内数据间的相关性，并选择合适的数据序列来进行预测的问题。但现有的预测网络模型主要存在2 个缺点：1）大部分网络采用自回归生成模式，由于网络特性[9]，随着预测时间的增长会导致预测中出现累积误差，从而影响预测精度；2）大部分网络其本质是探索目标序列的单一分布期望，面对不符合假设的序列，其预测效果往往不理想。

GAN 是一种通过网络的反向传播直接塑造输出分布的模型。受此启发，本文设计了一种将改进后的DA-RNN 网络和GAN 相结合的多维时间序列预测算法，利用GAN 网络中的判别器对DA-RNN 网络进行优化，从而在消除累积误差的同时加强网络对于随机变量的预测效果。受到Transformer 网络启发，本文采用多维注意力机制模型[10]对DA-RNN 网络进行改进，同时考虑到只有少数的历史数据在预测中起到决定性作用，因此本文利用 a-entmax稀疏映射[11-12]函数进行归一化变换，使得与当前预测无关的历史数据所占权重为零。

1 DA-RNN 算法改进

DA-RNN 算法是一种从仿生角度出发，模仿人类观察事物的机制提出的一种时间序列预测网络。网络利用编码器部分的注意力模型，实现从多维时间特征序列中挑选出与当前时刻相关性强的序列特征，并将其用于后续的预测。

1.1 提升网络运行速度

1.2 注意力模型改进

注意力模型是指网络根据循环神经网络上一时刻的隐藏状态，计算不同时刻的输入或当前时刻的不同输入与当前预测值的相关程度，从而给与输入序列不同的权重，使得网络更关注与当前时刻输出相关程度高的历史数据。传统的注意力机制包含 Query(Q)、Key(K)及 Value(V)三要素，算法通过计算某一特征空间中Q和K的相关性分数，经过归一化映射后成为V中各参数对应的权重值。但对于Q和K，相关研究表明，其各自应由多个相互解耦的特征组成，只在某一特征空间中计算二者的相关性分数，可能会导致结果不准确，进一步导致网络预测精度降低。本文引入多维度注意力模型，从多个子空间中计算Q和K之间的相关性分数，有效解决了相关性结果不准确的问题。

1.2.1 多维度注意力机制

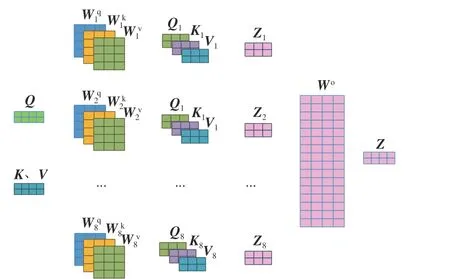
图1 多维注意力模型示意

1.2.2 稀疏映射

从图2 可以发现：当 α=1时，x=0部分对应的映射值不为0；当 α ＞1时，x=0部分的映射值为0，且随着 α值的增大，对应的映射曲线变化幅度越大。对应于注意力机制，随着 α值的增大，网络对于相关性分数高的历史数据会给与更高的权重值。

图2 不同 α 值下 a -entmax映射

1.3 网络优化目标改进

DA-RNN 网络中以最小化预测均方误差（mean square error，MSE）损失为优化目标。在满足预测值与真实值之间的残差为独立变量，且对于整个序列其方差不变的情况下，以MSE 有优化目标的模型能取得较好的效果，但对于不满足这一假设的序列，其效果并不好。结合分位数回归模型及GAN 网络中的判别器模型[13]，本文构建了新的网络损失函数，改进了网络的优化目标，使其在方差会发生变化或残差分布为非正态分布的序列上也能取得较好的效果。

分位数回归损失函数为

2 GAN 网络的构建

GAN 网络由生成网络和判别网络2 部分构成。生成网络目的在于通过训练生成与真实数据类似分布的数据，判别网络目的在于区分出生成的数据和真实数据。本文以改进后的DARNN 网络为基础构建生成网络。判别网络目的在于通过训练达到区分出生成网络生成数据和真实数据的目的。考虑到网络复杂度等因素，本文以全连接网络为基础，构建判别网络，网络具体结构见下表。

如表1 所示，网络由输入层，2 个隐藏层及输出层组成。其中，输入层大小为输入序列长度，输出层结果经过 Sigmoid函数映射为0～1 之间的值，表示当前输入为真实数据的置信度，值越接近1，表示当前输入值为真实数据的可能性越高；反之，输入数据为生成网络预测值的可能性越高。

表1 判别网络结构

3 实验验证

选用某公开纳斯达克指数数据集nasdaq100作为测试数据集，并选择数据集中的“AAL”参数作为预测指标，将本文算法与DA-RNN 算法进行对比，对本文算法的有效性和准确性进行评估。测试平台配置如表2 所示，数据集的特征数量为83，时间点数为40 561 个。

表2 测试平台配置

3.1 网络运行时间测试

针对1.1 节中利用GRU 网络单元替换LSTM网络单元，从而实现降低网络复杂度，提升网络运行速度的优化目标进行测试，分别选用滑动窗口序列长度T=10和T=50对网络运行速度进行测试，迭代轮次 (epochs)值均为50，在不同的测试轮次中，算法时间消耗时间t如图3 及图4 所示。

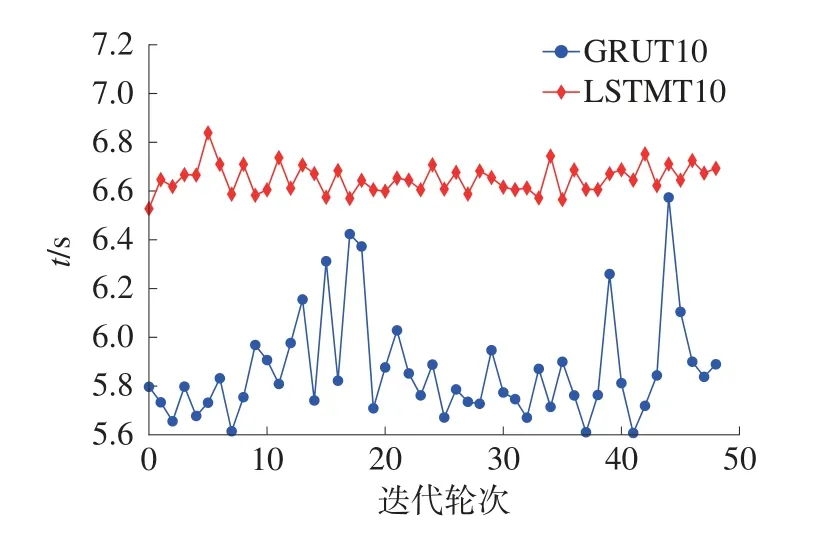
图3 输入序列长度为10 时网络运行时间对比

图4 输入序列长度为50 时网络运行时间对比

当T=10时，使用GRU 单元和使用LSTM 单元在运行时间上差距较小，约为1 000 ms；当T=50时，二者之间差距扩大到约5 000 ms。由此可见，随着输入序列长度的增加，利用GRU 单元替换LSTM 单元可以有效提升网络运行速度。

3.2 预测精度对比

本文选择数据集中“AAL”参数作为目标序列，使用sklearn 库中的MinMaxScaler 方法对数据集进行归一化预处理，使用MSE 作为预测结果衡量标准，分别对本文算法及DA-RNN 算法进行测试，具体模型配置如表3 所示。

表3 实验模型配置参数

本文算法与DA-RNN 算法对于“AAL”序列预测结果分别如图5 和图6 所示。

图5 本文算法预测结果

图6 DA-RNN 算法预测结果

由图6 可以发现，DA-RNN 网络在预测过程中存在较为明显的累积误差，随着预测时间的增长，网络的预测误差明显增大。而对比图5，本文提出的基于GAN 网络的时间序列预测算法则基本能消除累积误差对网络预测结果的影响。由此可见，本文算法明显优于DA-RNN 算法，原因在于RNN 网络在预测某一时刻值yˆt时，前一时刻预测值yˆt-1也会参与到其中，随着序列的增长，累积误差会越来越大，导致预测精度越来越低；本文结合GAN 网络，利用GAN 网络的判别器作为正则项来消除生成网络中的累积误差，并采用分位数损失作为网络优化目标，力求探索目标序列的完整分布，提高预测精度。2 种算法预测结果的MSE 损失LMSE如表4 所示。