一种改进的增强组合特征判别性的典型相关分析

高玉森，朱昌明，岳闻

上海海事大学 信息工程学院，上海 201306

多视角学习[1-2]是当前模式识别领域中的一个热点，吸引了许多学者进行研究。多视角学习旨在学习由多视角数据组成的多视角数据集的特征，并设计可行的分类器以对这些数据集进行分类。比较知名的多视角学习算法有协同训练、多核学习以及子空间学习等。假设有一个多视角数据集D，其中每个数据均包含来自2 个视角的特征，即 {(x1,y1),(x2,y2),···,(xn,yn)} 。 特征{(x1,y1),(x2,y2),···,(xn,yn)} 来 自 特 征 集X， 特 征{(x1,y1),(x2,y2),···,(xn,yn)}来自特征集Y。这里，X和Y也代表此数据集的2 个视角。多视角学习旨在从X和Y中学习并获得特征，从而设计一种可行的分类器。为了更好地学习特征，特征提取成为一种很好的方法，经典的特征提取方法是典型相关分析(CCA)[3-4]。CCA 旨在从2 个视角中寻找特征集之间的线性相关关系，处理分类任务时，CCA 首先提取出2 组典型相关变量，使得2 组数据间相关性最大；接着再利用这2 组典型相关变量的组合（串行或并行）进行后续分类，能够获得比只使用单组特征进行操作的更优的分类效果。在过去的几十年中，CCA 及其变体已成功应用于许多领域，例如图像处理[5-6]、模式识别[7-8]以及脑电分析[9-10]等。

尽管CCA 在特征提取方面具有不错的性能，但CCA 本身是一种无监督降维方法，没有利用样本的类别信息。为了解决这个问题，首先提出了判别典型相关分析(Discriminative CCA, DCCA)[11]，DCCA 在CCA 的基础上既考虑了2 个视角间的相关关系，又考虑了视角内数据的相关关系。在最小化视角类内相似度的同时最大化视角类间相似度，提取出了比CCA 更有判别性的相关特征。但DCCA 依旧采用对各视角提取的特征本身直接进行组合及分类输入，并没有针对分类任务来直接优化组合特征本身。针对这个问题，周旭东等[12-13]提出了一种优化组合特征的有监督降维方法：增强组合特征判别性的CCA(CECCA)，CECCA 通过结合判别分析，优化组合特征本身及其组成部分，获得了更利于分类的组合特征。

CCA、DCCA 和CECCA 等算法在处理分类任务时，仅关注于隐藏在“干净”数据中的信息，这些信息完全属于学习任务中存在的任何类别，称其为目标数据。Universum 学习提出了将关于应用领域的先验知识融入到学习过程中，这些知识与目标数据具有相同域但不属于任务目标类，被称为Universum 数据。已经提出了许多具有Universum 学习的学习机，例如陈晓红等[14]提出了一种改进的CCA(ICCA)。在ICCA 中，必须同时考虑目标数据之间的相关性和Universum 数据之间的相关性。这意味着在使用ICCA 时，特征提取会使用更多先验信息。ICCA 通过执行相关性分析，使目标数据上的相关性尽可能大，而Universum 数据上的相关性尽可能小。它可以获得具有与目标数据最大相关性和与Universum 数据最小相关性的理想方向。

CECCA 和ICCA 在特征提取方面都比CCA具有更好的性能，但是ICCA 和CECCA 都没有利用彼此的优势。故将Universum 学习引入到CECCA 中，通过结合判别分析与Universum 学习提出了一种改进的增强组合特征判别性的典型相关分析(ICECCA), ICECCA 在CECCA 的基础上，通过结合Universum 学习，实现在利用训练数据与Universum 数据获得更多先验信息的同时，做到对组合特征相关性与判别性的联合优化。

1 相关工作

1.1 典型相关分析

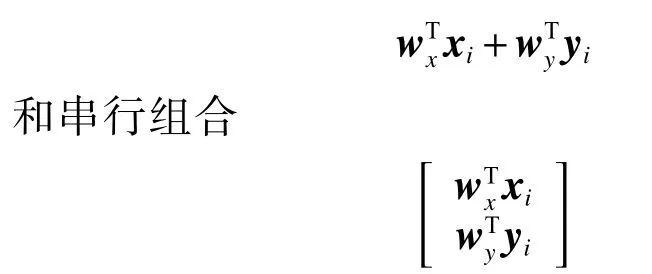
1.2 增强组合特征判别性典型相关分析

CCA 是一种无监督学习方法，做分类任务时直接利用提取出的特征，并没有利用样本的类别信息，缺少良好的判别性。CECCA 在CCA 基础上加入了一种判别性惩罚项，通过结合判别信息，使得抽取的特征更利于分类。

1.3 改进的典型相关分析

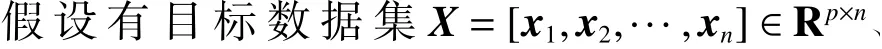
2 改进的增强组合特征判别性的典型相关分析

由于ICCA 和CECCA 具有彼此所没有的优势，ICCA 引入了Universum 学习，获得了更多的先验知识；CECCA 利用判别分析，实现对双视角特征相关性与判别性的同时优化。二者相比于CCA 都能更好地处理分类问题，但是它们都没有利用彼此的优势。因此在这里可将Universum学习与CECCA 结合，提出一种改进的增强组合特征判别性的典型相关分析(ICECCA)，以便能够同时利用Universum 学习以及判别分析。ICECCA 在ICCA 和CECCA 的基础上，通过结合二者优势，实现在获得更多先验信息的同时，做到了对目标样本特征相关性与判别性优化。

3 实验

在本节中，为了评估所提出的ICECCA 的性能，在多个数据集上进行了对比实验，比较的方法包括CCA[3]，ICCA[14]和CECCA[12]。使用的数据集包括人工数据集以及多特征数据集。

3.1 在人工数据集上的性能比较

为了公平起见，在本实验中采用和文献[14]中相同的人工数据集分布（分布是相同的，但是数据的生成是随机的），生成一个具有2 个目标类的双视角（X视 角和Y视角）数据集，每个类包含100 个二维样本，Universum 数据集包含200 个样本。X=[X1,X2]表 示为目标样本的X视角，其中Xi(i=1,2)是 第i类的样本矩阵。它们均通过高斯

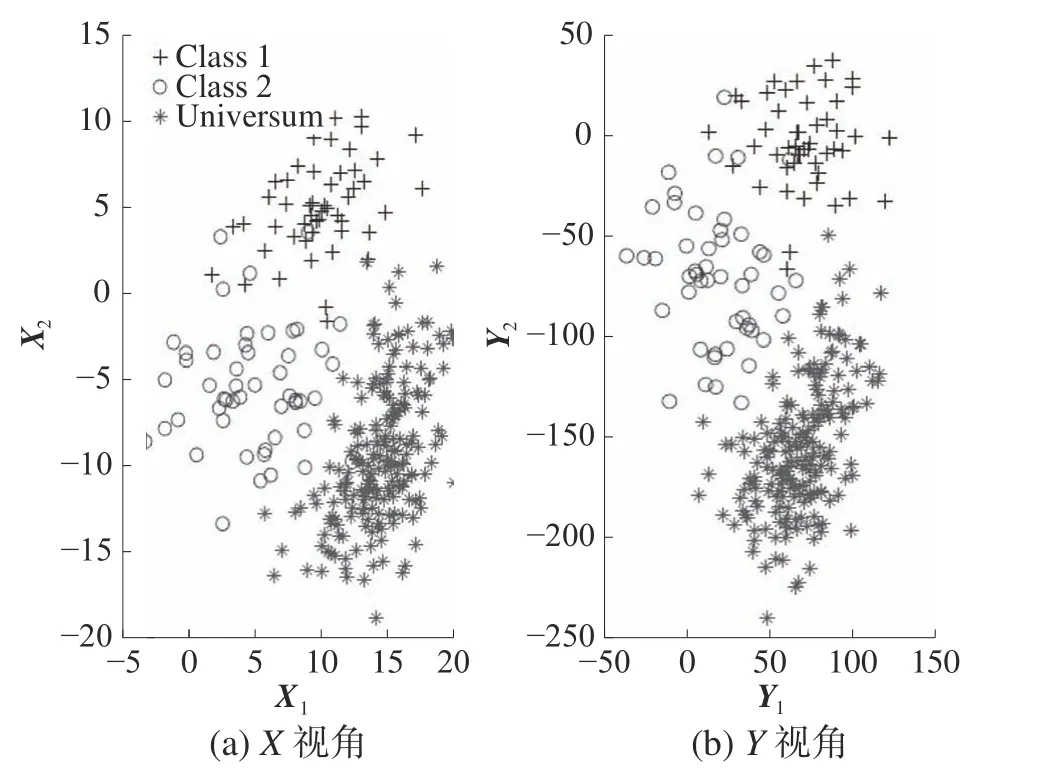
图1 训练样本分布

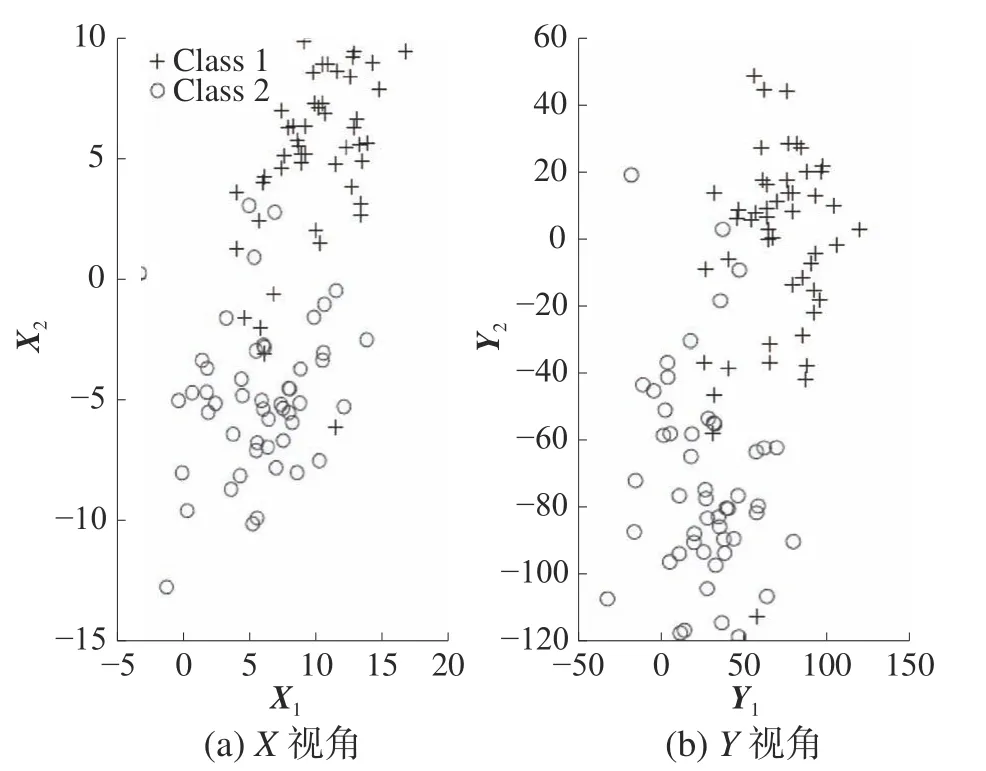
图2 测试样本分布

在实验中，参数 η的设置参考文献[14]，即η=2-4。图3 和图4 分别展示了从训练和测试样本中提取的第一对特征的分布。

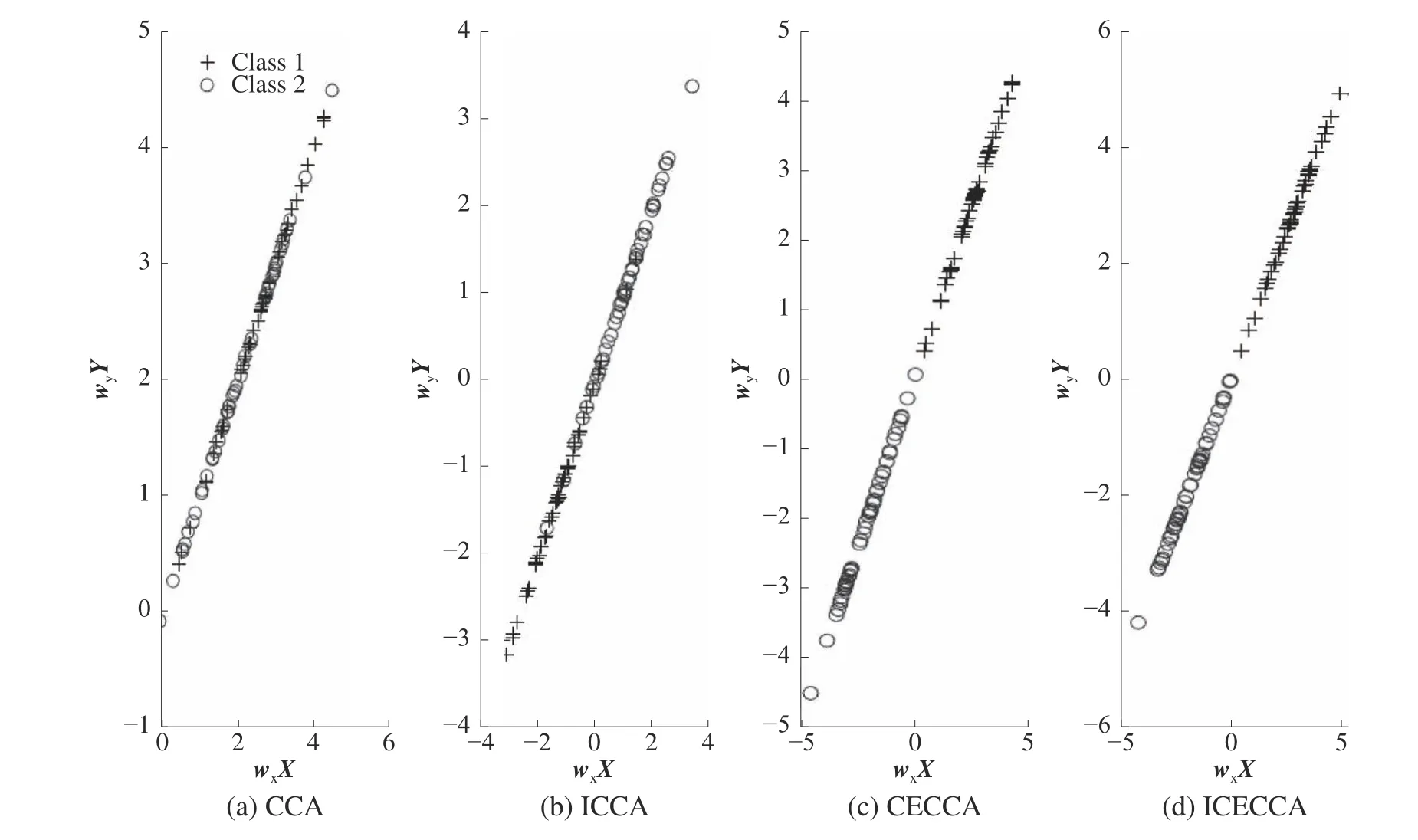
图3 X 视角和Y 视角的一维特征（训练样本）

从图3 和图4 中可以看出，CCA 虽然揭示特征间的线性相关关系，但2 类间存在严重重叠；ICCA 引入了Universum 学习，获得了更多的先验信息，取得了比CCA 更优的结果，但依旧存在重叠。CECCA 与ICECCA均引入类信息，2 类在第一对特征上的分布基本无重叠；并且ICECCA 还引入了Universum 学习，相比于CECCA，ICECCA得到的结果类内更紧凑，类间距更大，这说明ICECCA 所获取的组合特征更优。

3.2 在多特征数据数据集上的性能比较

在多特征数据集方面，采用从UCI 机器学习存储库中选择的多特征数据集(multiple features data set，MFD)[15]，该数据集由“0”-“9”的手写数字组成，每类200 个样本，共2 000 个。MFD 具有6 个特征，分别是轮廓相关性、字符形状的傅里叶系数、Karhunen-Love 系数、2×3 窗口中的像素平均、Zernike 矩特征以及形态学特征。这些特征的名称和维度分别为（fac，216），（fou，76），（kar，64），（pix，240），（zer，47）和（mor，6）。对于此数据集通常从6 个特征中随机选择2 组作为X视角和Y视角，因此共有15 种双视角组合。

根据表1 的结果可以发现，与CCA 相比，ICCA 和CECCA 的优越性分别表明了Universum数据的先验信息以及增强组合特征的判别信息对于提取多视角数据的特征都具有很好的意义。ICECCA 明显超过CCA，从4%～20%不等。ICECCA在15 种组合中的10 种上胜过CECCA。准确性的提高证明，同时利用Universum 数据编码的先验信息以及增强组合特征的判别信息对于多视角特征提取更有意义。ICECCA 的性能并不总是优于CECCA，原因可能是有些Universum 样本提供的先验信息不足，算法的性能受Universum 数据和目标样本的组合影响。

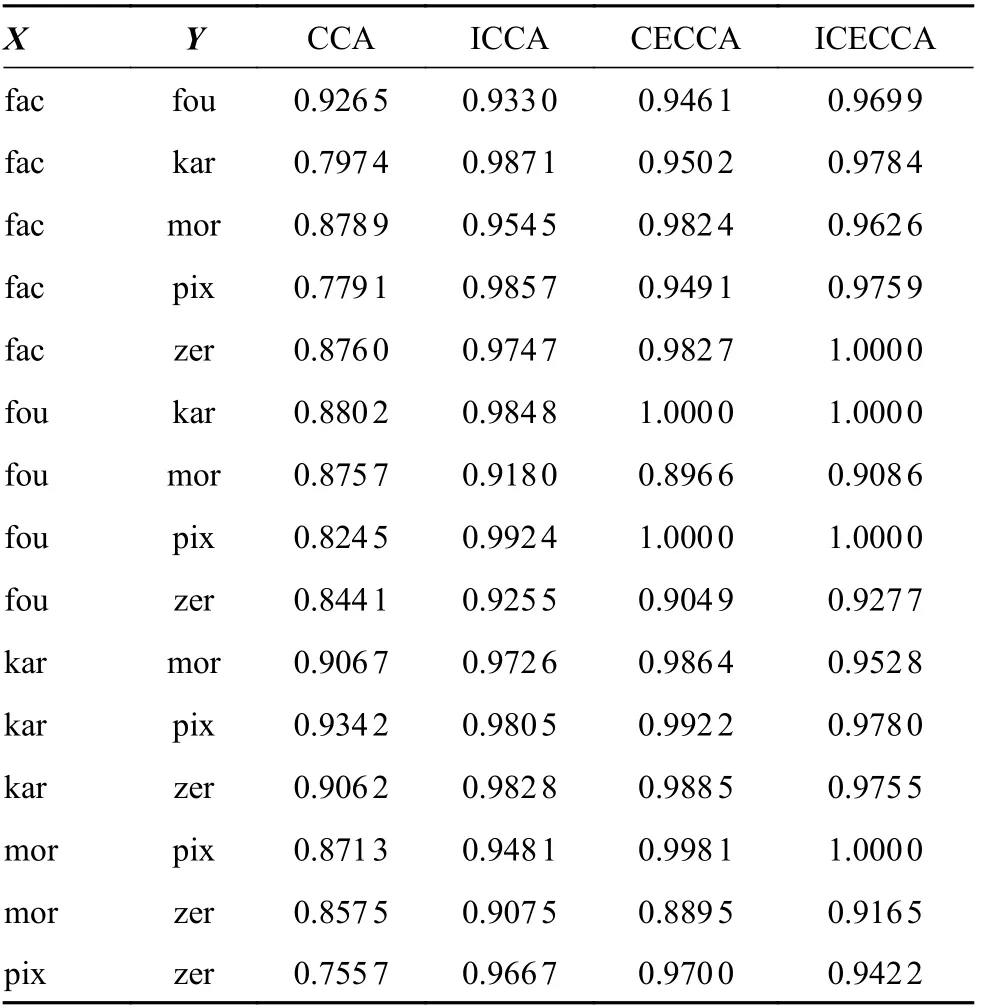
表1 在多特征数据集上识别准确率

3.3 在UCI 数据集上的性能比较

在本节中，从UCI 机器学习存储库中选择5 种常见的多类别单视角数据集作为实验数据。有关使用的数据集的详细信息见表2。

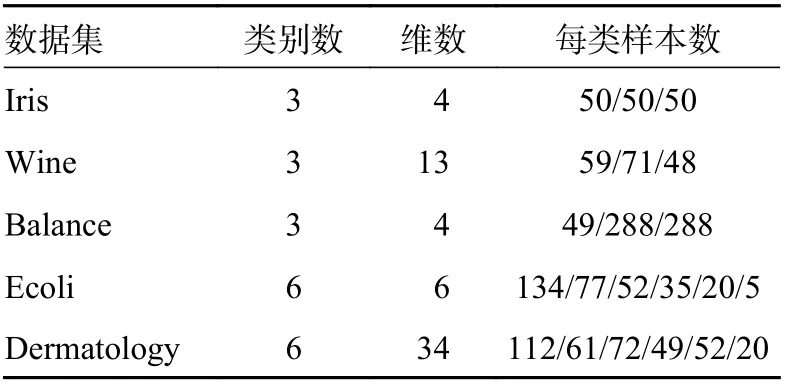
表2 UCI 数据集

由于每个数据集都是单视角，因此将它们本身视为X视角的数据，而对于Y视角的数据，根据文献[14] 中所述的方法来生成。例如对于Iris 鸢尾花数据集，它具有3 个类别xi,i=1,2,3。如果xi属于第1 类，则Y视角中的对应样本表示为yi=(1,0,0)T；如果xi属于第2 类，则yi=(0,1,0)T；如果xi属 于类别3，则yi=(0,0,3)T。其他数据集的Y视角根据其类别数进行相应的设置。

显然，不同的Universum 数据包含不同程度的域信息。假设目标数据集具有n个类别，采用2 种不同的方法来生成Universum 数据：1）将前n-1 类作为目标样本，将最后一个类作为Universum数据；2）选择与上述相同的目标样本，并根据高斯噪声生成具有与目标样本相同的数量和维度的的Universum 样本, 例如Iris 数据集的高斯噪声Universum 数据，如图5 所示。

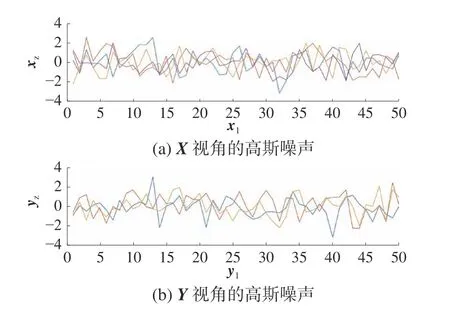
图5 通过高斯噪声生成的Universum 数据

对于这些数据集，仍然先采用CCA、ICCA、CECCA 和ICECCA 来 提 取 特 征， 接 着 使用SVM 根据提取的特征进行分类。参数 η=2-20，对于每个目标样本，随机选择每个类的一半作为训练，其余部分进行测试，并重复进行10 次实验。平均结果如表3 所示。其中ICCA_A 和ICCA_B分别表示将最后一类作为Universum 数据以及使用高斯 噪 声 作 为Universum 数 据，ICECCA_A 和ICECCA_B 同理。

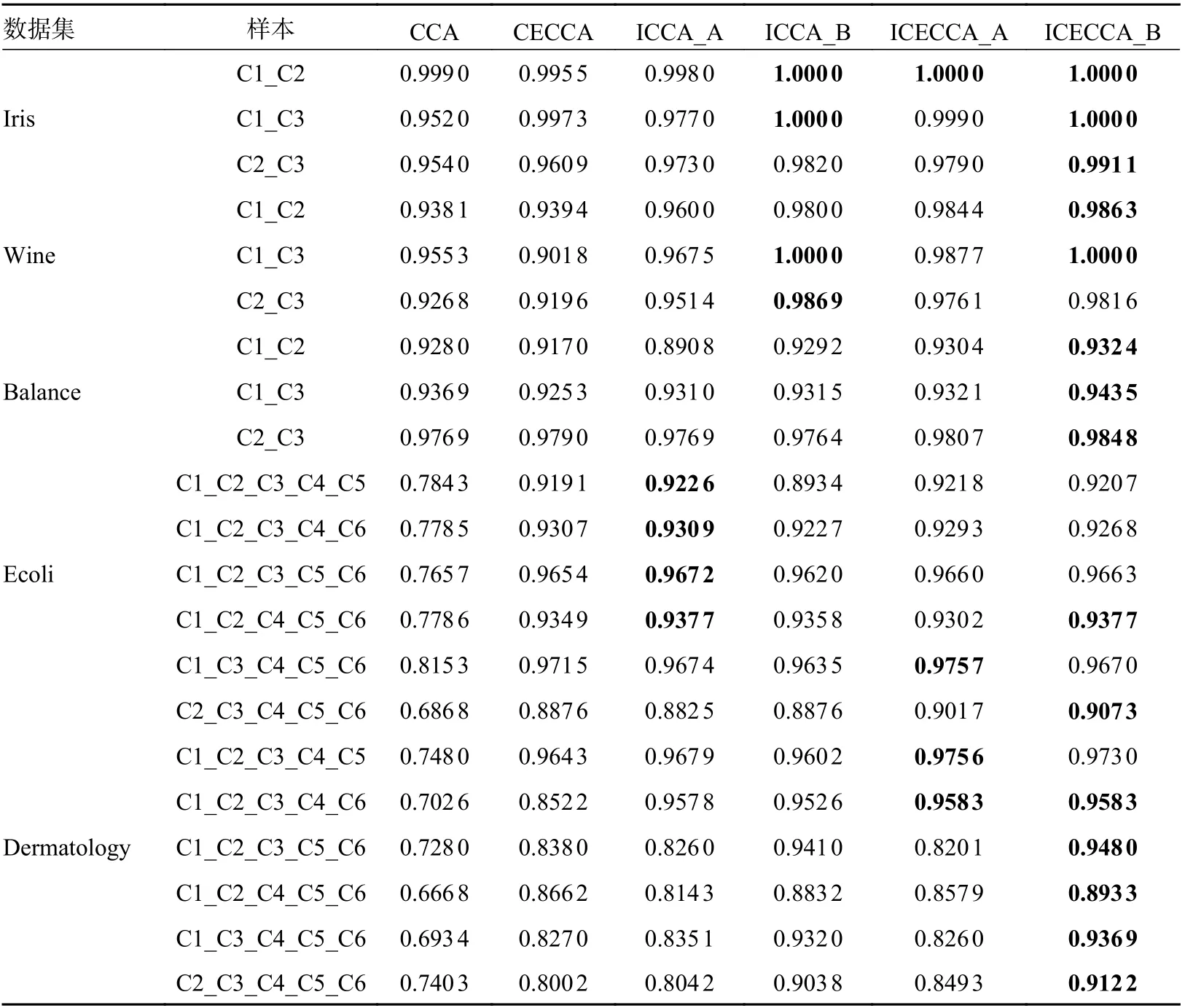
表3 在UCI 数据集上识别准确率

从表3 结果可以发现：1）几乎所有情况下，ICECCA 的 分 类 准 确 率 都 高 于CCA、ICCA 和CECCA，达到了最佳性能（以粗体显示）。结果验证了Universum 学习与样本判别信息的结合在降维中的有效性，Universum 学习提高了低维空间中不同类别样本的可分离性；2）ICCA_A 与ICCA_B、ICECCA_A 与ICECCA_B 识别结果的差异表明，并非所有种类的Universum 数据都包含针对即将完成的任务的有意义的信息，而同种类不同数量的Universum 样本也会对分类结果产生影响。因此，当Universum 与目标样本无关或Universum 样本数量过少，也即Universum 数据包含的先验信息过少时，基于Universum 的学习效果会很差。

4 结论

本文通过将ICCA 的先验知识与CECCA 的优化组合特征结合在一起，提出了一种改进的增强组合特征判别性的典型相关分析ICECCA，为了验证所提出方法的有效性，对包括人工、多特征数据集以及经典的UCI 数据集进行了实验，并采用现有的多视角特征提取算法进行了对比。相关实验验证了本文提出的算法的有效性.

本文为了减少时间开销使用Universum 学习来进行信息增强，但目前已经有很多其他方法可以生成额外的无标签样本，如对抗网络等，未来可以采用对抗网络等方式更好地增强样本信息。

目前深度学习是一个非常热门的研究领域，提出了许多与深度学习相关的特征提取算法，如深度典型相关分析(Deep CCA)[16]，相关实验已经验证了Deep CCA 可以很好地解决多视角特征提取问题，受此启发，未来将尝试把Universum 学习与Deep CCA 相关算法相结合，更好地解决多视角特征提取问题。