基于前摄效应的不耐烦行为建模与双向行人流动态*

张琦 渠静

(北京交通大学交通运输学院,北京 100044)

不耐烦情绪是一种因人而异的心理因素,且随环境实时变化.本研究构建了基于元胞自动机的行人微观模型,并用其研究了双向行人流在不耐烦行为决策影响下的动态特征.模型定义了潜在势能场表达行人对可用空间的占用倾向,合理体现双向流行人决策的前摄效应.提出在行人运动过程中,根据瞬时状态测量、记录和更新行人个体不耐烦水平的方法,并以此触发个性化行为.对比研究了3 种不同的不耐烦行为模式的作用效果.仿真试验结果显示,与不考虑不耐烦行为相比,当不耐烦水平用于触发横跨行为时,双向流在速度、流率和等待时间方面的表现均有改善;当不耐烦用于直接计算行人对有限空间的竞争力时,这3 项指标则在大部分密度水平下均呈恶化.针对不耐烦作用强度与决策阈值的参数灵敏度分析显示了模型在不耐烦作用表现方面的灵活性.同时,分场景的仿真试验还揭示了低比例慢速行人、步道宽度及混合行为模式等对双向流效率的作用.

1 引言

关于行人双向流行为的既有研究揭示了行人群集现象源于个体的协作行为.针对现实世界中公共区域采集数据的调查和对情景实验统计数据的研究表明:行人流的自组织,尤其是步道生成对双向流起着至关重要的作用[1,2].随着密度的增加,双向流比单向流效率更高[3],这也可能是自组织效应增强的结果[4,5].行人步道生成有助于有效缓解正面冲突[6],并防止形成僵局[7].因此,无论采用连续模型[8,9]还是离散模型[10-14],步道生成一直是行人双向行为模型验证的主要指标.然而,在不同情况下,行人对协作的态度是多变的.Nagatani[15]采用元胞自动机模型的实验研究表明,行人在低密度时倾向自由移动,而高密度时则试图生成步道.李明华等[16]构建了改进的格子气模型再现低密度下对向行人流不会出现分层现象的特性.Feliciani和Nishinari[17]对自组织步道生成的研究表明,步道生成后平衡的双向行人流十分稳定,然而步道生成的过程中则要求行人最大程度地横向移动.这解释了为什么平衡的双向流在低密度下效率高,但会快速导致高密度下的死锁.事实上,行人之间的协作是基于特定条件的,至少与密度[14,18,19]有关.一些研究探讨了高密度的建模解决方案[20,21],然而,问题的核心仍取决于协作机制是否正确合理地表达.

在现实世界中,行人个体根据用户最佳原则在微观层面上做出运动决策,在宏观层面上则体现为可能的系统最佳结果.例如,行人个体选择适时跟随前方的同向行人,避免与对向行人碰撞,这种利己的个体行为对应的群体现象即为步道生成,且提高了特定条件下整个群体的效率.因此,行人之间的所谓“协作”,实际上是个体基于其局部环境的个性化行为的集成表现.目前针对各种个性化行为的大量研究普遍集中在人群疏散场景上.Fu 等[22]引入了模糊理论表现性格各异的行人对危险信息的反应.Haghani 等[23]通过实验揭示了适度的竞争压力有利于中等规模人群的疏散,并引发了对传统的“快即是慢”效应的深入讨论.Fu 等[24]和Weng等[25]则分别探讨了行人差异化行为能力和速度对疏散效率的重要作用.针对行人流的研究也揭示了个性化行为的强大作用,包括随机减速[26]、右行偏好[27]、偏移倾向[28]以及跟从行为[29-31]等.基于个性化行为的协作可能提升群体效率,也可能导致群体表现的恶化,尤其是在高密度争夺有限空间[32,33]的条件下.关于人群疏散的研究表明,个体过于积极的疏散行为会导致整体效率降低[34,35].可见,群体现象的决定因素是个体的决策原则和行为模式,有必要正视个性化行为对群体表现的重要作用.

个性化行为视角的引入打破了由统一运动规则触发群体效应的常规思路.在双向行人流中,协作表现为基于个性化行为决策的步道生成过程.这里的个性化行为取决于行人个体对同向和对向行人潜在作用的反应,包括运动状态下的碰撞规避和停滞状态下的行为决策.碰撞规避基于行人对来自其他行人潜在作用的预判.Suma 等[36]和 Lü等[30]分别改进了势能场模型和社会力模型用于表现行人的预见性行为.Jin和Guo[37]针对上下楼梯场景改进了元胞传输模型,利用异向行人对元胞势能的影响驱动路径选择行为.这些研究揭示了前摄效应在行人行为研究中的重要性.停滞状态则源于排队或冲突导致的拥堵,并进一步引发行人的不耐烦情绪.近年来不少行人流动态研究[38,39]中也考虑到了行人的心理状况,不耐烦已被证明是影响人群疏散效率的一个关键因素[40,41].本研究假定不耐烦是可能引发双向流中个性化行为的一个因素,并进一步导致不同的群体表现.根据日常经验,在不耐烦的情况下,行人会更加渴望移动,更具竞争力或更加积极地寻找可用空间,从而也会影响其预判和碰撞规避的相关决策.值得注意的是,个体之间的不耐烦程度各不相同,而且不耐烦状态会随着行人周围的情势发生持续变化.因此,前摄效应和不耐烦触发的行为决策对双向流的步道生成过程至关重要,进而影响双向流的群体表现.

既有研究显示了基于元胞自动机的模型[13-15,21,24-26,32,41-43]在捕捉与重现个性化行为方面具有强大的表现力和有效性.本文构建基于元胞自动机的模型,通过定义潜在势能场合里表现双向流中行人决策的前摄效应.针对不耐烦触发的个性化行为及其作用,提出了行人个体不耐烦水平的计量和更新规则,对比研究了由不耐烦触发的3 种行为模式对双向流的作用效果.

2 行人双向流中的前摄效应与不耐烦行为

冲突和死锁是制约双向行人行为建模的瓶颈问题之一.在真实世界中,行人并不会盲目前进直至拥堵,而是在行走过程中通过不断观察和调整避免冲突和停滞[14,33],这种前摄效应在建模中尤为重要.行人在进行前摄决策时,同向和异向行人的相对数量发挥了潜在作用.通常同向行人相对较少的一方更倾向于转向换道,而人数相对较多的一方则具备更明显的优先权保持原前进方向.

如图1 所示,行人群体Ln和Rn对向行走,行人在行走过程中实时表示自己对前方空间的占用倾向.kLn和kRn分别代表两个群体的行人释放占用倾向的作用距离.从时刻t过渡到时刻t+1 时,行人L1(身后没有同向行人)感知到对向行人的占用倾向后随即选择换道至左侧以避免与R1及其身后的人碰撞.

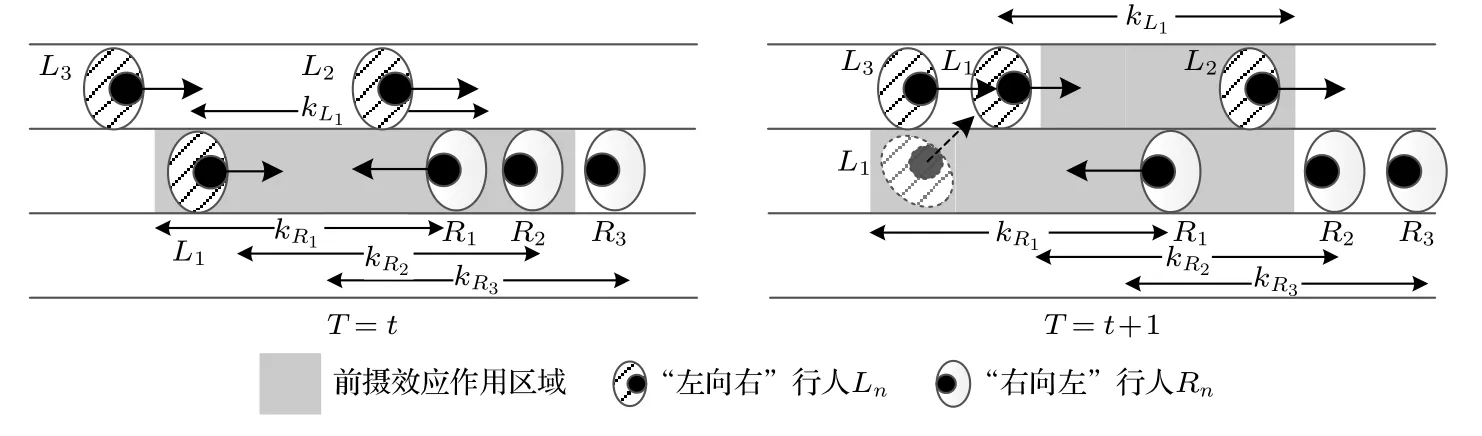
图1 双向行人的前摄效应Fig.1.Proactive effect of bi-directional pedestrians.

本文提出的模型中定义了由行人作用和更新的潜在势能场来表现上述前摄效应.每个行人个体对其前方空间的占用倾向以潜在势能场的方式予以记录、累加和比较.详细规则见3.2 节.

前摄效应的表达机制为缓解面对面冲突提供了途径,但随着人群密度的增加,拥堵不可避免.被迫停止和等待的行人可能产生不耐烦心理,这在真实世界中十分普遍.因此,不耐烦的行人可能基于其不耐烦的程度进行行为决策.一方面,不耐烦水平在行走过程中是动态变化的,当行人停止前进等待较长时间时,不耐烦水平较高,当其继续以期望速度行走时不耐烦水平可能降低甚至消失.另一方面,不耐烦对行人的行为决策可能产生不同的影响.一个不耐烦的行人可能横跨换道,也可能在占用前方有限空间方面更具竞争力.同向和异向不同个体之间差异化的动态不耐烦水平,使得每个行人面对的环境更加复杂和难以预测.本文针对3 种不同的不耐烦行为模式进行建模和对比研究.不耐烦水平的变化规则以及行为模式的表达详见3.3 节.

3 不耐烦行人运动模型

3.1 基础定义

仿真模型基于一个以方形单元格为基础结构的二维系统.单元格边长为 0.45 m,每个单元格在任一时间步只z 能由一名行人占用或者空闲.如图2所示,有两类行人以相反的方向相向运动,Lefts(L)代表“左向右”行人,Rights(R)代表“右向左”行人.每个行人作用并更新其影响的单元格上的潜在势能场值,从而生成和更新潜在势能场.潜在势能场影响并触发行人的移动决策.

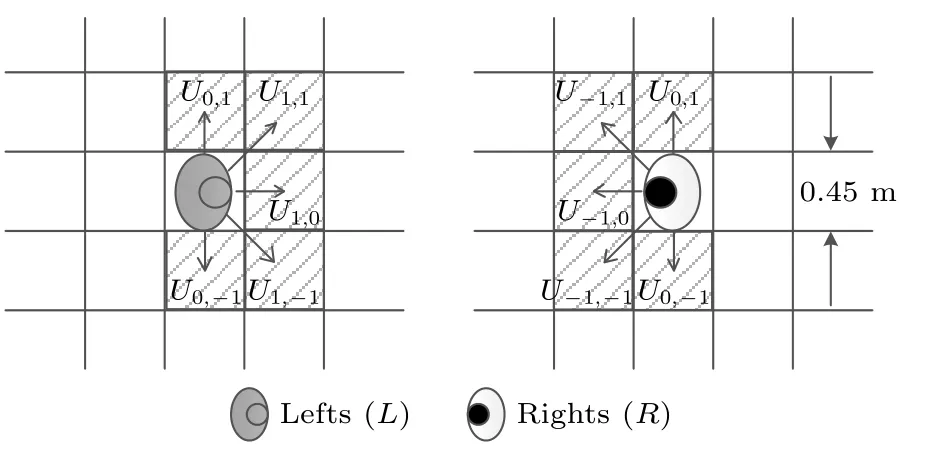
图2 行人移动的方位及概率Fig.2.Pedestrian movement space and tendency.

如图2 所示,每个行人每时间步尝试移动至其周围的5 个格子,具体位置与其行走方向相关.Ui,j表示行人移动至格子 (i,j) 的转移概率.对于任意一个格子,行人对其设定和更新两个潜在势能场值:和,分别表示通过右向左行人和左向右行人进行赋值的潜在势能场值.某个行人向其周围相邻格子的 (i,j) 的转移概率Ui,j由该格子的和值确定.每时间步每个行人向其影响距离内的所有格子设定潜在势能场值,每个格子累计所有对其作用的行人的潜在势能场值,并更新该时间步内格子的和.下个时间步,每个行人依据自己周围格子的和及其空闲情况,确定自己移动到哪个格子或原地等待,并进一步再次对其影响距离内的所有格子设定潜在势能场值.行走方向为d的行人的转移概率如公(1)式所示.

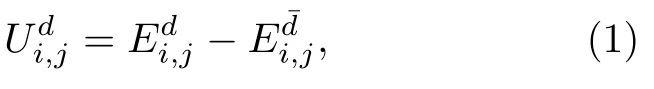
通过比较转移概率,行人移动到周围5 个格子中转移概率最大的空闲单元格,转移概率则取决于双向行人的影响.行人移动可以通过持续更新潜在势能场值和转移概率值来实现.潜在势能场值更新的详细规则见3.2 节,行人移动规则见3.3 节.模型的变量和参数见表1.

表1 参数及其物理意义Table 1.Some parameters and the corresponding physical meanings.

3.2 潜在势能场值更新

对于每个格子,两个潜在势能场值El和Er分别由可对其施加影响的“左向右”和“右向左”行人进行更新.行人可影响的格子包括其正在占据的格子以及未来时间步内倾向于占据的格子.

1)行人影响其正在占据的格子

以图3 中“左向右”行人L为例,一旦L移动到其前方3 个格子之一(图3(b)和图3(c)),目标格子的El将被行人L更新为El+1;如果L横跨至左侧或右侧的格子(图3(d))或停在目标格子不动(图3(e)),目标格子的El将不会被行人L更新.因此,El的增加表示曾占用该格子的行人成功前进,该格子值得后方其他与行人L同向的行人考虑选择.

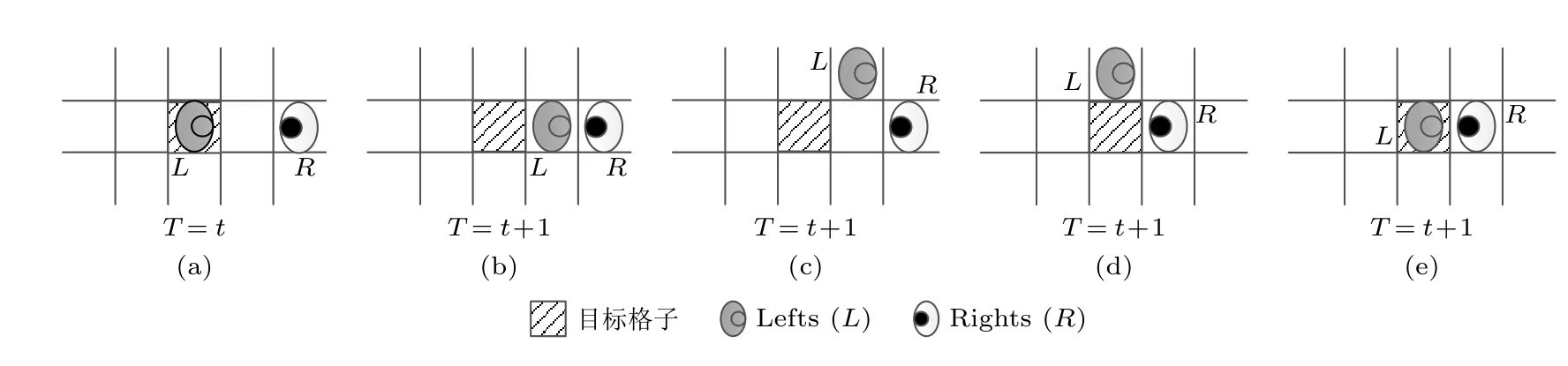
图3 正在占据的格子的潜在势能场值更新Fig.3.Potential field value update for occupied cells.

2)行人影响其未来时间步内倾向于占据的格子

如果行人前进,前方k个格子为其未来时间步内倾向于占据的格子;如果行人原地等待,将尝试选择左前或右前的格子,则其左前和右前格子为其未来时间步内倾向于占据的格子.如图4 所示,每个时间步内,一旦行人L移动到其前方3 个格子之一(图4(b)和图4(c)),或横跨至左侧或右侧的格子(图4(d)),则其前方k个格子的El将被行人L更新为El+1;如果L停在目标格子不动(图4(e)),则其左前和右前格子的El将被行人L更新为El+1.同时,行人R前方k个格子的Er将被行人R更新为Er+1.因此,El的增加表示该格子对“左向右”行人更具吸引力.

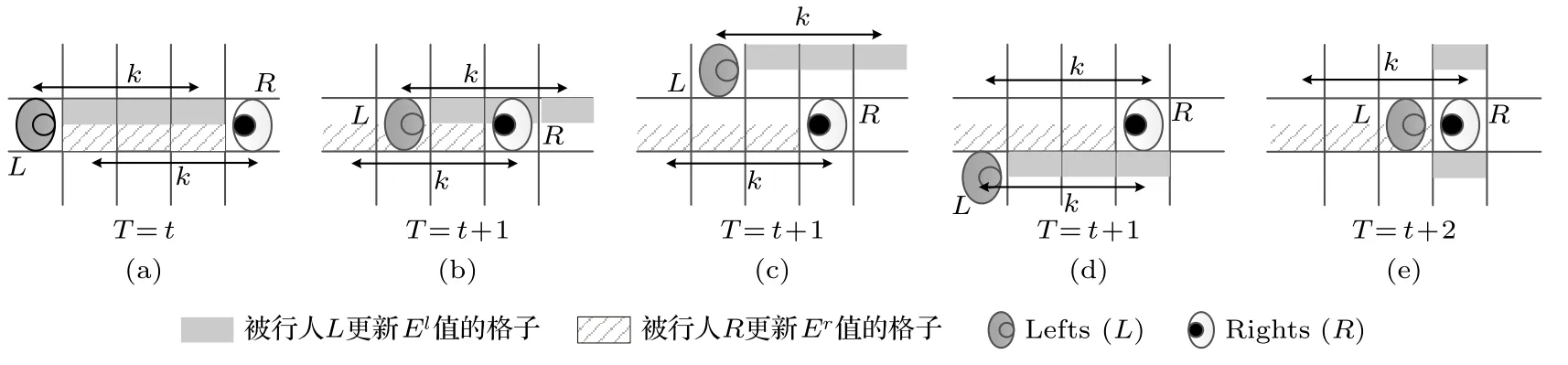
图4 倾向于占据的格子的潜在势能场值更新Fig.4.Potential field value update for interested cells.

初始状态下无人移动时每个格子的潜在势能场值均为0.行人更新其正在占据的和倾向于占据的格子的潜在势能场值.每个时间步内无人占用的格子的El和Er衰减为El×β和Er×β,β为潜在势能场值的衰减率.

每个时间步内,每个人为自己影响范围内的格子设定潜在势能场值,每个格子则依据所有对其产生影响的行人的作用进行累加并更新其潜在势能场.对于某个格子,如果更多的“左向右”行人影响该格子,或更多的“左向右”行人占据并经过该格子,则该格子的El应当大于Er,对于“左向右”而言其转移概率UEl-Er越大,反之亦然.

3.3 行人移动规则

3.3.1 不考虑不耐烦的行人移动规则运动过程中,行人依据转移概率Ui,j向前方、左前和右前3 个格子中的一个移动.如果3 个格子均不空闲(如被他人占用),则原地等待直至这3 个格子有空闲.行人前进方向上前k个格子被视为倾向占用的影响区域.不考虑不耐烦的基本移动规则如表2 所列(以“右向左”行人及由其确定的Er为例).

表2 不考虑不耐烦情况下“右向左”行人R 的基本运动规则Table 2.Basic movement rules a pedestrian of Rights without considering impatience.

3.3.2 考虑不耐烦的行人移动规则

移动过程中,如果3 个格子均不空闲,行人被迫原地等待,直至3 个格子中有格子空闲.不耐烦情绪在行人原地等待无法移动时产生.不同行人的不耐烦水平存在差异,对于同一个人,不耐烦水平也是变化的.行人的不耐烦水平随着原地等待时间的增加而提升,一旦其再次开始移动,则不耐烦水平下降甚至消失.

令it代表行人在时间步t的不耐烦水平.运动过程中,每个行人依据即时状态更新其it.更新规则如下:

如果行人不移动,令

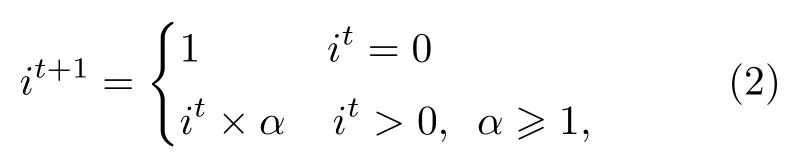
如果行人移动,令

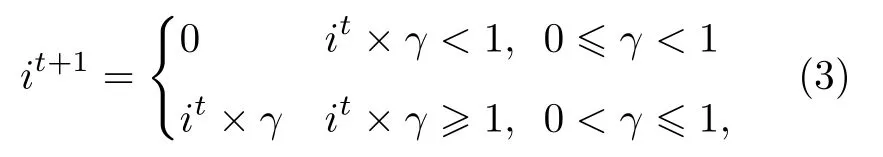
其中α(α≥ 1)为不耐烦水平增长率,γ(0 ≤γ≤1)为不耐烦水平衰减率.

行人在不耐烦心理的作用下可能更积极地尝试搜索空闲格子,可能在停滞不前时选择横跨,也可能引发更强烈的移动意愿.本文针对这3 种可能的不耐烦行为模式展开研究.

模式1不耐烦水平i作为横跨行为的触发条件(图5(a));

模式2不耐烦水平i作为直接参数用于确定多人竞争同一目标格子时的优先权(图5(b));

模式3不耐烦水平i用于计算转移概率,并作为间接参数用于确定多人竞争同一目标格子时的优先权(图5(c)).

令δ≥ 0表示影响决策的不耐烦水平阈值.如图5(a)所示,“右向左”行人R不耐烦水平为i＞δ时,该行人在前方3 个格子不空闲时决定横跨换道,即不耐烦水平大于阈值作为横跨行为的触发条件(即模式1).图5(b)中,目标格子的所有竞争者中,“左向右”行人L(不耐烦水平为i＞δ)具备最高的不耐烦水平,则L可以优先移动至该目标格子,即不耐烦水平i作为直接参数用于确定多人竞争同一目标格子时的优先权(即模式2).不考虑不耐烦因素时采用随机选择规则处理冲突(表2),模式2 则引入不耐烦水平处理冲突.图5(c)中,行人依据i×Ui,j计算转移概率选择目标格子,目标格子的所有竞争者中,“右向左”行人R(不耐烦水平为i＞δ)具备最大的i×Ui,j值,则R可以优先移动至该目标格子,即不耐烦水平i作为间接参数用于确定多人竞争同一目标格子时的优先权(即模式3).

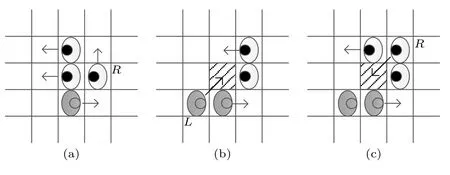
图5 3种不耐烦行为模式 (a) 模式1,不耐烦作为回避的触发因素(R 不耐烦水平i ＞ δ);(b) 模式2,不耐烦作为估计优先权的直接参数(目标格子有4 名潜在竞争者,其中,L 的不耐烦水平i 最高且大于δ);(c) 模式3,不耐烦作为估计优先级的间接参数(R 的i×Ui, j 最高且不耐烦水平i 大于δ)Fig.5.Three patterns of impatient behaviors:(a) Pattern 1,impatience as a trigger of sidestep (i of R ＞ δ);(b) Pattern 2,impatience as a direct parameter to estimate priority (4 potential competitors for the target cell,L has the largest i (i of L ＞ δ) among all of the potential competitors for the target cell);(c) Pattern 3,impatience as an indirect parameter to estimate priority (R has the largest i×Ui, j (i of R ＞ δ) among all of the potential competitors for the target cell).

以一个“右向左”行人为例,其考虑不耐烦行为的行动规则如表3—表5 所列.

表3 模式1 的规则Table 3.Rules of Pattern 1.

表4 模式2 的规则Table 4.Rules of Pattern 2.

表5 模式3 的规则Table 5.Rules of Pattern 3.

4 试验结果分析

采用多智能体可编程建模平台NetLogo 6.0.3[44]搭建仿真试验环境.通过设置不同的参数组合,在不同条件下实施双向行人仿真试验,用于分析不同场景下不耐烦行为模式的作用.N表示行人总数(双向数量对等分别为N/2).定义密度为N/格子总数,以符号ρ表示.T表示仿真时间步长.

图6 给出了随着仿真时间步推进双向流步道自组织形成过程.当T=0 时,一定数量的行人(ρ=0.3)随机分布在22.05 m×22.95 m 的空间内,双向行人数量对等.行人依据表2 所列的规则运动.当T=25 时,步道初步成型,T=100 时,步道形态更加清晰.可见,前摄型潜在势能场的触发和更新对于捕捉双向行走过程中的自组织效应是有效的.

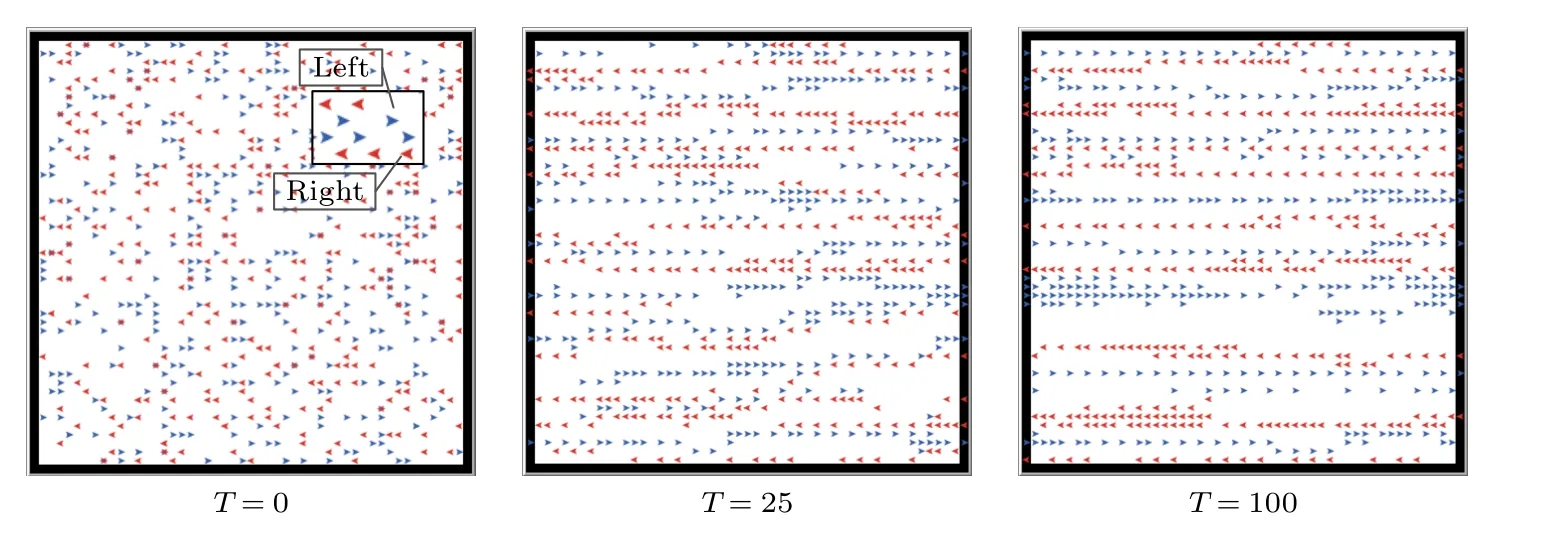
图6 基本规则下的步道形成Fig.6.Lane formation with Basic movement rules (ρ=0.3).

4.1 前摄型潜在势能场及不耐烦效应的作用分析

仿真试验针对3 个不耐烦行为模式及一个不考虑不耐烦的基本模式进行对比分析.图7 给出了不同密度水平下行人触发的潜在势能场的动态情形.较深的颜色代表该格子具备较大的潜在势能场值.图中Basic 代表基本模式(不考虑不耐烦行为),Pattern 1—3 分别代表模式1—3 (考虑不耐烦行为).总体而言,基本模式下行人相对集中分布,同向行人由于排队停滞而产生局部的轻微拥堵,并触发了较强的潜在势能场.考虑不耐烦的3 个模式下行人则相对分散,步道之间间隙更小,边界也相对模糊.考虑不耐烦行为时,不同程度的拥堵主要源自对向行人的面对面冲突.

图8 给出了模式1 下不同密度水平行人个体的不耐烦水平.具有较高不耐烦水平的行人呈现较深的颜色.当密度较小时(ρ=0.1),没有停滞和等待,不耐烦水平较低.密度较大时(ρ=0.5),拥堵较明显,部分行人开始变得不耐烦,平均不耐烦水平提升.

4.2 不耐烦行为模式及参数的作用分析

4.2.1 不耐烦行为模式的作用分析

用于结果分析的统计指标定义如表6 所列.每次仿真试验前50 个时间步用于启动试验,指标的记录和统计基于后800 时间步的情况.仿真试验采用的参数取值为k=3,β=0.8,α=1.5,γ=0.5,δ=0.依据3.1 节的定义,试验参数取值反映了前摄影响范围为前方3 个格子,不耐烦水平直接影响决策,并且不耐烦作用力量为中等水平的情况.参数条件变化及对应的灵敏度分析见4.2.2 节,4.2.3节和4.3 节.

图9 给出了速度(Speed)和流率(Flow rate)在不同密度水平下的变化曲线,本研究涉及的基本模式(Basic)和3 个不耐烦行为模式(Pattern 1—3分别代表模式1—3)与经典的CA 模型(Blue,2001)进行对比.结果表明:基本模式与经典CA模型的趋势最为接近.而考虑不耐烦的3 种模式则表现出较大差异.模式1 显示了与经典CA 模型类似的速度曲线趋势,但具有更高的绝对值.这样的曲线形态揭示了合理的横跨换道行为有助于提高双向行人流的效率.模式2 在低密度和高密度下的速度和流率均较低,意味着如果不耐烦水平决定行人争抢优先空间的竞争力,则对行走效率产生负面影响.这与图12 中步道较宽且边界较为模糊的形态具有一定关联.模式3 在密度较低(ρ=0.2,0.3)时具备最高的速度和流率,但密度大于等于0.4 时却突然恶化.这与图12 中呈现的形态一致,ρ=0.3时行人有条不紊地移动,ρ=0.5 则出现明显拥塞.

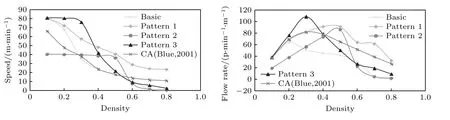
图9 不同密度水平下速度和流量的差异Fig.9.Comparison of speed and flow rate under different density levels.

如图10 所示,大多数密度水平下基本模式等待时间最长,表明不耐烦行为对减少行人的平均等待时间有积极的影响.模式1 在大多数密度下等待时间最短,在高密度时尤为明显.模式2 在较低和较高密度下均具备3 种不耐烦模式中最长的等待时间.模式3 在较低的密度下获得最短的等待时间,但随着密度大于0.4 而快速增加.

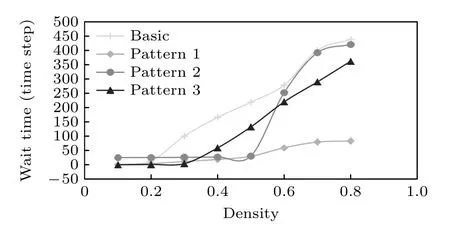
图10 不同密度水平下的等待时间差异Fig.10.Wait time under different density levels.

4.2.2 参数δ 的作用分析

参数δ≥ 0表示不耐烦水平影响决策的阈值.δ=0表示只要行人不耐烦(i＞ 0),就依据相应的模式规则触发其不耐烦行为.δ＞ 0表示行人只有在不耐烦水平i达到特定阈值δ时,才会按照不耐烦模式规则触发其行为.图11 给出了在不同δ值作用下速度随密度的变化关系.在不同的不耐烦模式下,δ对速度的影响明显不同.δ=0 时模式1 具备所有密度水平下的最高速度,而δ＞ 0 时其具体取值对速度的影响不大.对于模式2,当ρ≤ 0.5时,δ＞ 0 会导致明显的速度下降,但ρ=0.6 时速度值会随δ值的增大而不同程度地增大.δ的取值对模式3 的速度影响不大.

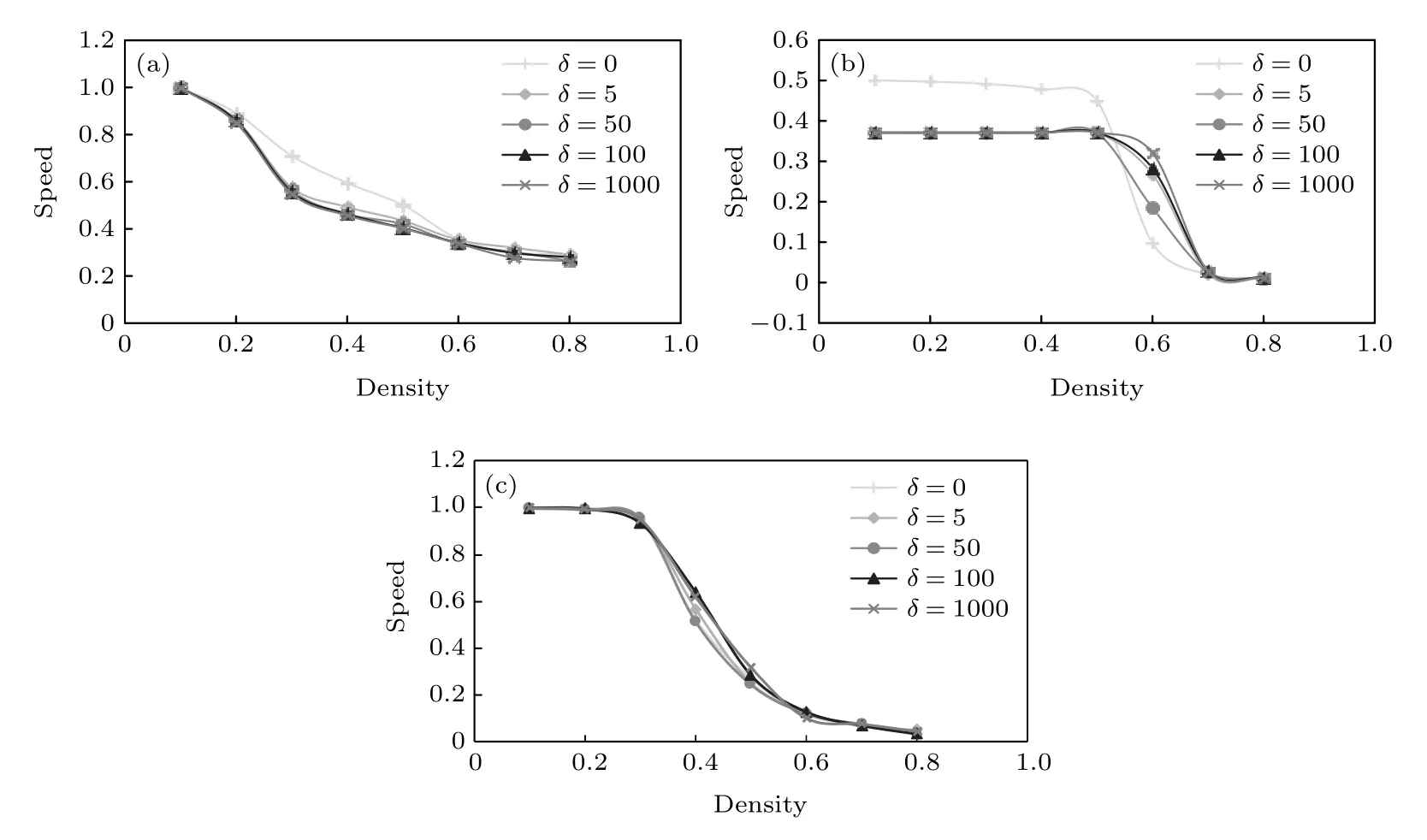
图11 不同δ 情况下速度和密度的关系 (a) 模式1;(b) 模式2;(c) 模式3Fig.11.Speed vs.Density under different δ:(a) Pattern 1;(b) Pattern 2;(c) Pattern 3.

4.2.3 参数α和γ的作用分析

参数α和γ分别表示不耐烦水平的增长率和衰减率.α=1.2和γ=0.2表示不耐烦水平缓慢增加和快速下降,说明不耐烦的作用力量相对较弱.而α=1.8和γ=0.8 则代表不耐烦水平快速增加并缓慢下降,说明不耐烦的作用力量相对较强.

对于模式1(图12(a)),更强的不耐烦作用力得到更高的速度,反之,较弱的不耐烦作用力则得到较低的速度.α和γ不同取值时得到的等待时间差异不明显(图12(b)).对于模式2(图12(c)和图12(d)),最弱的不耐烦作用力(α=1.2和γ=0.2)在所有密度水平下均得到最低的速度和最长的等待时间.而最强的不耐烦作用力(α=1.8和γ=0.8)只在ρ≤ 0.4 时才能获得最高速度和最短的等待时间.当ρ≥ 0.5 时,中等程度的不耐烦作用力表现更好.模式3 则反映出不同的特征(图12(e)和图12(f)).不耐烦作用力的增长和衰减对ρ=0.4—0.5 的速度和等待时间表现出相反的影响,即最弱的不耐烦作用力得到最高的速度和最长的等待时间,而最强的不耐烦作用力则得到最低的速度和最短的等待时间.

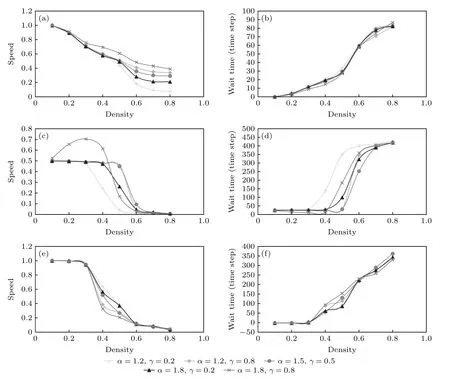
图12 不同 α和 γ 下的速度和等待时间随密度的变化趋势 (a) 模式1 的速度;(b) 模式1 的等待时间;(c) 模式2 的速度;(d) 模式2 的等待时间;(e) 模式3 的速度;(f) 模式3 的等待时间Fig.12.Speed and wait time vs.density under different α and γ:(a) Speed with Pattern 1;(b) wait time with Pattern 1;(c) speed with Pattern 2;(d) wait time with Pattern 2;(e) speed with Pattern 3;(f) wait time with Pattern 3.

4.3 慢速行人作用分析

考虑行人群体存在速度差异,部分行人(如老人或行动不便者)速度较低.与正常速度的行人相比,假设这类慢速行人对前方区域的影响范围较小,且其不耐烦的作用力量相对较弱.本模型正常速度行人每时间步移动一格,即0.45 m,3 个时间步相当于1 s,走行速度约为1.35 m/s;慢速行人每2 个时间步移动一格,走行速度约为0.675 m/s.在仿真试验中,慢速行人的行为参数取值为k=1,α=1.2,γ=0.2.正常速度行人参数取值为k=3,α=1.5,γ=0.5.图13 给出了仿真试验中连续时间步内捕捉到的正常速度行人对慢速行人的超越过程.

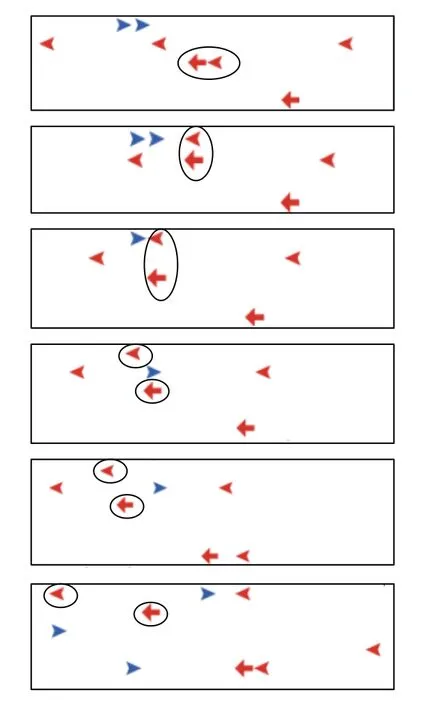
图13 仿真试验中正常速度行人对慢速行人的超越过程(局部图) 注:其中三角形代表正常速度行人,箭头形代表慢速行人Fig.13.Overtaking process between pedestrians with normal speed and slower speed (Partial screenshot) Note:the triangles represent pedestrians with normal speed and the arrows represent pedestrians with slower speed.

设定慢速行人占总人数比例S分别为0%,10%和20%,试验结果如图14 所示.与全体行人均为单一正常速度(S=0%)相比,当10%或20%的行人为慢速行人时,行人的平均速度普遍降低,但慢速行人对不同的不耐烦作用模式的影响存在差异.模式1 的速度衰减在各密度水平下均较为显著;模式2 的速度衰减在密度大于或等于0.5 时才较为明显;而模式3 的速度衰减则在各密度水平下均相对平缓.说明在特定密度水平下,适度不耐烦行为对于缓解低比例慢速行人的冲击具备积极作用.

图14 不同慢速行人比例下速度和密度的关系 (a) 模式1;(b) 模式2;(c) 模式3Fig.14.Speed vs.density under different proportion of slower pedestrians:(a) Pattern 1;(b) Pattern 2;(c) Pattern 3.

4.4 步道宽度的作用分析

为了研究不耐烦行为模式在不同步道宽度W条件下的表现,选取3 种不同宽度进行仿真试验.其中W=22.05 m 为理论试验取值,依据《地铁设计规范》(GB50157-2013)中规定岛式站台最小宽度为8 m,以及《铁路旅客车站设计规范》(TB 10100-2018)中规定特大型站旅客进站、出站通道最小净宽12 m,结合本模型的单元格尺寸0.45 m,分别取W=8.1 m,11.7 m;步道长度统一为22.95 m.

实验结果显示,以W=22.05 m 的试验结果为基础,随着步道宽度的减小,各密度水平下的速度和流率基本呈现减小趋势,密度高时速度和流率的衰减尤为明显.当步道宽度减小为11.7 m 时,双向流率降低了约44%—79%;当步道宽度减小为8.1 m时,双向流率降低了约63%—86%.对比几种行为模式,考虑不耐烦行为的模式1 在各密度水平下的平均速度衰减最为明显,但两个宽度水平下衰减程度相差不大,衰减率分别为38.4% (W=8.1 m)和36.7% (W=11.7 m);模式3 的速度衰减则对宽度较为敏感,衰减率分别为20.3% (W=8.1 m)和12.9%(W=11.7 m).

4.5 不耐烦行为模式共存下的作用分析

行人在产生不耐烦情绪时,可能会采取不同的行为模式.仿真试验模拟采用不同行为模式的行人共存条件下的双向流行为,以研究模式共存条件的作用效果.图15 中“Pattern 1+2”和“Pattern 1+3”分别表示行人中随机选择一半的人采用行为模式1,另一半人采用行为模式2 或3 的情形.如图15 所示,在混合模式下,速度、流率和等待时间的曲线形态、最大值和临界值均与单一模式不同.基本上,混合模式的各项统计值是两个单一模式的中间值.

图15 混合模式不同密度下速度、流率、等待时间的变化 (a) 速度与密度关系;(b)流率与密度关系;(c) 等待时间与密度关系Fig.15.Speed,flow rate and wait time under different density levels with mix impatience patterns:(a) Speed;(b) flow rate;(c) wait time.

5 结论

本文构建了不耐烦行为模型研究不耐烦行为对双向行人流的影响.通过定义由个人产生和更新的潜在势能场表现行人之间的前摄效应,并触发行人的行为决策.在行人运动过程中,根据瞬时状态测量、记录和更新每个人的不耐烦水平,并通过可控参数调节不耐烦的变化动态.模型支持对兼顾个体多样性和运动过程动态性的不耐烦水平的实时表达,并将其作为行人个性化行为的触发因素.本文提出并比较了3 种不同的不耐烦行为模式.

基本图和相关统计数据揭示了3 种不耐烦行为模式在不同情况下的作用效果.模式1 使双向流具备最高的速度和流率、最短的等待时间;模式2 具备最低的速度和流率,且在大多数密度水平下等待时间最长;模式3 在较低的密度水平下具备最高的速度和流率以及最短的等待时间,但在高密度水平下各项指标都急剧恶化.不耐烦水平影响决策的阈值δ,对不同的不耐烦行为模式有不同的影响.由不耐烦水平增长率α和衰减率γ表达的不耐烦水平的作用力量对行人双向流的效率也具备影响.通过调整前摄效应和不耐烦水平的相关参数,模型支持对慢速行人差异化不耐烦行为的表现.在特定密度水平下,适度不耐烦行为对于缓解低比例慢速行人对双向流效率的冲击具备积极作用.同时,不同的不耐烦行为模式在步道宽度减小时的速度衰减程度也体现出差异性.在现实世界中,人群通常由不耐烦水平各异的行人组成,这些行人按照不同的不耐烦行为模式进行行为决策.本文中混合不耐烦模式场景的试验揭示了双向流基本图的不同特征.更加全面的结论有赖于进一步深入的研究分析.

本文构建的行人模型为探索不耐烦行为对双向行人流的作用提供了量化方法,试验结果揭示了不耐烦行为模式对双向流基本图关键因素的作用,为理解个体个性化行为对群体运动效率的作用机理提供了理论支持.由于定量观测行人的不耐烦行为特征较为困难,本文的研究局限于对特征规律的理论探讨,后续研究工作中可借助虚拟现实等试验手段获取行人不耐烦心理及行为决策的动态特征,有望进一步标定和完善本文提出的模型.