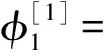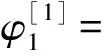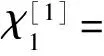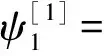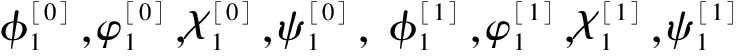非线性光纤中耦合非线性薛定谔方程怪波的研究
2022-04-15雷宇祥张毅菲商慧晶
雷宇祥,宋 妮,张毅菲,商慧晶
(中北大学 理学院, 太原 030051)
怪波,也称为畸形波、奇异波,它是海洋里突然出现又很快消失的一种具有时空局域性的巨大水波[1-2]。由于人们对怪波发生的地点、波高等具体信息无法提前知晓,因而海洋怪波巨大的破坏力严重影响着船舶的航行安全、海洋工程的建设及相关人员的生命安全。近年来,一些研究者在金融[3]、玻色-爱因斯坦凝聚[4]、流体力学[5]及空间等离子体[6]等领域中发现怪波。在海洋学和非线性光学等领域中,非线性薛定谔(NLS)方程的有理解常被用来分析和研究怪波[7-10]。随着科技的不断发展和实际问题的复杂性,多组分耦合非线性薛定谔方程能更好地刻画非线性现象,且有更丰富的局域波动力学性态。Priya等[11]采用Hirota双线性法研究了耦合广义非线性薛定谔方程的局域波解,推导出由该方程的孤子解、呼吸子解构造怪波解的方法。Zhao等[12]利用广义达布变换研究了二分量耦合非线性薛定谔方程的高阶怪波解,发现不同形式的怪波可以同时出现。目前,利用耦合非线性薛定谔方程对怪波深入研究也是许多学者关注的话题。
在非线性光纤中,2个正交偏振电磁波在非线性光纤中的传播可用耦合非线性薛定谔方程来描述,
(1)
式中:q1,q2是2个相互作用的波包络函数;变量x代表归一化距离;t代表延迟时间;星号“*”代表复共轭。方程(1)的最后一项是相干耦合项,且自相位调制系数与交叉相位调制系数不同。
若方程(1)没有相干耦合项,则为Manakov系统中的二组分耦合NLS方程,Song等[13]利用广义达布变换计算得到方程的高阶局域波解并分析局域波之间的相互作用,He等[14]推导出在特殊条件下方程的非对称怪波解。基于有相干耦合项的方程(1),霍丛哲[15]利用达布变换研究该方程的一阶对称怪波解和非对称怪波解,但未对该方程的高阶怪波解进一步研究分析。
本文在一阶怪波的基础上,利用广义达布变换探究方程(1)的二阶怪波解,分析二阶怪波的非线性动力学特性。
1 广义达布变换
方程(1)是可积的,对应的Lax对方程如下:
(2)
式中λ为光谱参数,
这里,I是2阶单位矩阵。
假设Φ=(φ,φ,χ,ψ)T是方程(2)在谱参数为λ时对应的解。对Φ做变换Φ[1]=TΦ,T是达布矩阵。构造达布矩阵T=λI-HσH-1,其中
在此基础上,构造方程(1)的广义达布变换。
假设Φ=(φ1,φ1,χ1,ψ1)T是方程(2)对应于λ=λ1-iη2的解,η是小参数。在η=0处对Φ1进行泰勒展开,有
(3)
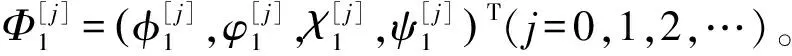
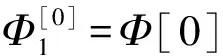
(4)
其中
Φ1[N-1]=(φ1[N-1],φ1[N-1],
χ1[N-1],ψ1[N-1])T
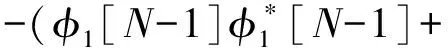
f[N-1]=(φ1[N-1]χ1[N-1]+
(φ1[N-1])2)
d[N-1]=(φ1[N-1]ψ1[N-1]-
(φ1[N-1])2)
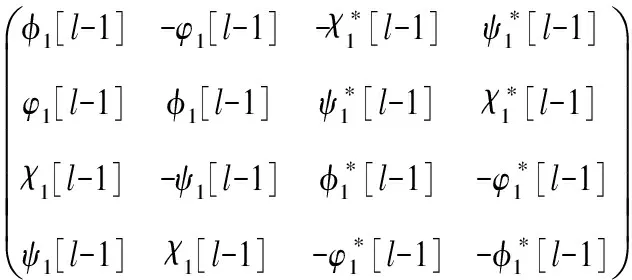
2 二阶怪波解
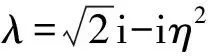
(5)
其中,Ci(i=1,2,3,4)是复常数,η是小参数,
M=diag(e-2it,e-2it,e2it,e2it)
在η=0处对Φ(λ)=(φ1,φ1,χ1,ψ1)T进行泰勒展开,有
(6)
利用广义达布变换,根据方程(4)可知,方程(1)的二阶怪波解q1[2],q2[2]形式如下,
(7)
1) 当Ci=0(i=1,2,3),C4≠0时,q1[2],q2[2]有相同的表达式,方程(1)有一组对称怪波解。此时q1[2],q2[2]是基本的二阶怪波形式,一个大幅值周围有4个较小幅值,如图1所示。
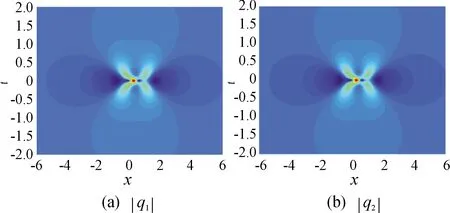
图1 二阶怪波等值高线图
2) 当Ci=0(i=1,2),C3=1,C4=γ1eiθ取不同值时,有q1[2]=q2[2],是一组对称怪波解。此时二阶怪波由3个一阶怪波组成,呈三角形结构分布,且相互影响,如图2所示。随着参数θ取值的变化,怪波在时间和空间上的位置也有规律性的变化。
3) 当Ci=0(i=1,4),C3=1,C2=γ2eiθ取不同值时,q1[2],q2[2]有不同的表达式,即q1[2]≠q2[2],方程(1)有一组非对称怪波解。此时q1[2],q2[2]与文献[14]中的一阶波形图相比,在对应位置演化为2组波峰,且在中心处形成一组波峰,但中心不在原点,如图3所示。在图3(a),图3(b)中,参数取θ=0,γ2=0.5,q1[2]和q2[2]的等值高线图分别有时间和空间对称性。在图3(c),图3(d)中,参数取θ=0.5π,γ2=0.5,q1[2]和q2[2]的等值高线图呈中心对称分布。
4) 当C2=C4=0时q1[2]和q2[2]经过2次广义达布变换可得到一阶怪波。
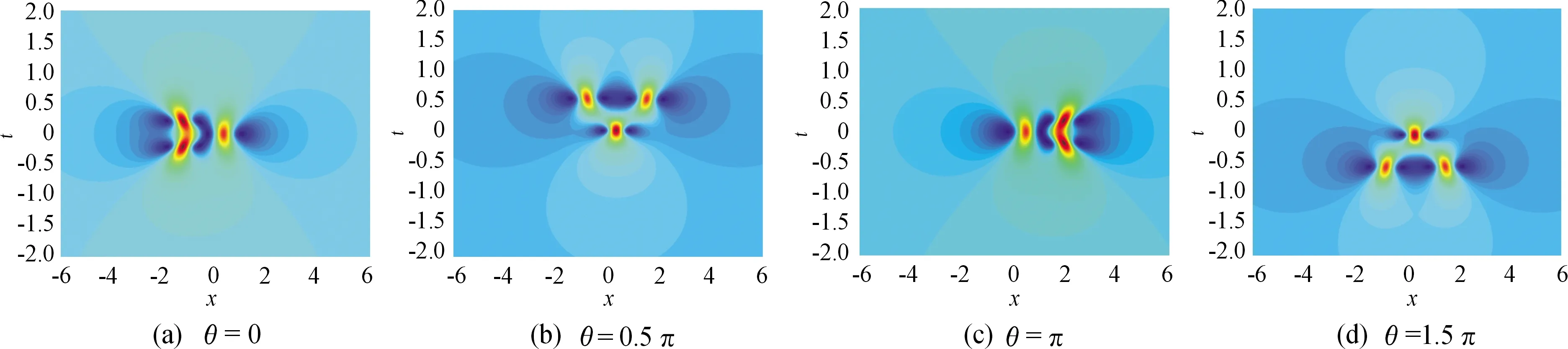
图2 γ1=1,|q1|=|q2|时,二阶怪波等值高线图
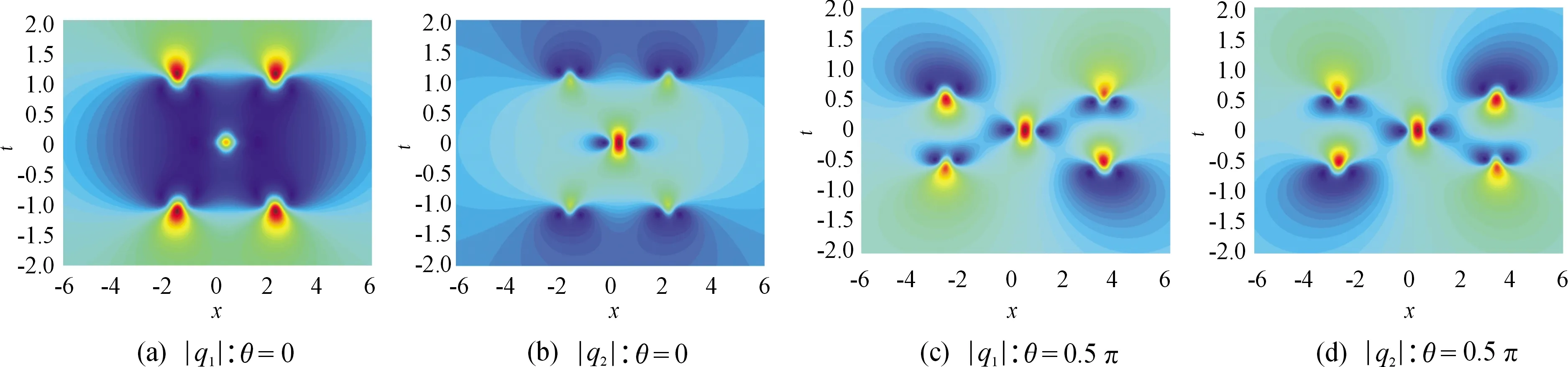
图3 γ2=0.5,|q1|≠|q2|时,二阶怪波等值高线图
3 结论
利用广义达布变换推导出耦合非线性薛定谔方程N阶怪波解的迭代公式,基于一阶怪波解的研究,给出了方程对称二阶怪波解和非对称二阶怪波解的表达式。最后通过选择适当的参数值进行数值模拟研究二阶怪波的动力学特性,发现了新结构的二阶怪波。这些结果在一定程度上可以解释海洋怪波的不对称性。