带有周期性名义变量的混合型数据聚类分析

肖枝洪，颜 伟

(重庆理工大学 理学院， 重庆 400054)

聚类分析是研究事物分类或分组的基本方法。聚类分析的目的是把要分类的对象按一定的规则分成若干类，属于同一类的对象在某种意义上倾向于彼此相似，而属于不同类的对象倾向于彼此不相似，从而使人们易于从纷繁复杂的数据中发现有价值的规律。聚类算法被广泛应用于客户细分、图像修复、蛋白质序列预测、模式识别等领域[1-4]。目前，国内外对单纯的数值型变量的观测进行聚类的算法[5-8]和单纯的名义变量(或属性变量)的观测进行聚类的算法[9-12]已经较为成熟。然而在实际问题中，如金融经济、生命科学、航空航天、汽车制造和移动通信等领域，存在大量的由数值型变量观测和由名义变量(或属性变量)观测组成的混合型数据，且有的名义变量的观测还具有某种周期性。尽管混合型数据的分类具有较高的实际应用价值，但针对此种混合型数据的相似性刻画和以此为依据进行聚类分析的方法仍不成熟。

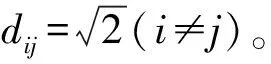
针对上述研究中存在的问题，对带有周期性名义变量的混合型数据中的周期性名义变量观测值进行合理量化，以改进周期性名义变量的观测值之间相似性度量的不足；给出周期性名义变量的观测值之间的距离公式，与数值型变量观测之间的距离公式相结合，提出具有周期性名义变量的混合型数据观测之间的新距离公式来度量样品间的相似性，并以此为依据对该类数据进行分类。

1 样品间距离公式以及类间距离公式

1.1 样品间距离公式

在聚类时，假设有n个样品，每个样品都有p个指标，xij表示为第i个样品的第j个指标的观测值。那么以xij为元素的观测数据矩阵X为：

根据X可以计算样品之间的相似性统计量，进而将X的所有样品进行分类。

1.1.1数值型变量观测之间的距离

假设X为单纯的数值型变量观测所构成的观测数据矩阵，为了不发生混淆，这里将其记为N,样本量为n，指标(特征)个数为p。任取数据集N中的2个样品Xi=(xi1,xi2,…,xip)和Xj=(xj1,xj2,…,xjp)，其距离定义为

(1)

1.1.2属性变量观测之间的距离

假设观测数据矩阵X仅由单纯的属性变量或名义变量的观测构成，记为C，其样本量为n，指标(特征)个数为q。任取数据集C中的2个样品Xi=(xi1,xi2,…,xiq)和Xj=(xj1,xj2,…,xjq)。此时用连续型数据观测之间的距离公式来计算属性变量观测之间的距离已经失效，目前大多学者采用汉明距离进行计算，见式(2)。

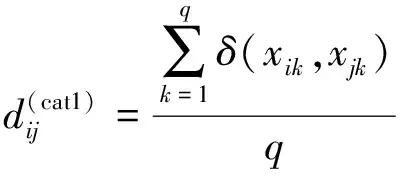
(2)

也有研究者引入李克特量表对属性数据进行量化，见式(3)。

(3)

依据式(3)得到初始距离矩阵为：

如前所述，按照式(2)或式(3)来计算周期性名义变量的观测值两两之间的距离是不合理的，故在此引入新的方法对周期性名义变量的观测值进行合理量化，并在此基础上提出周期性名义变量的观测值两两之间的距离公式，其具体做法如下：

假设周期性名义变量Y有k种不同的水平，分别为Y1,Y2,…,Yk，对应将复平面上的单位圆k等分，单位圆上对应点的取值分别为Y1,Y2,…,Yk，如图1所示。

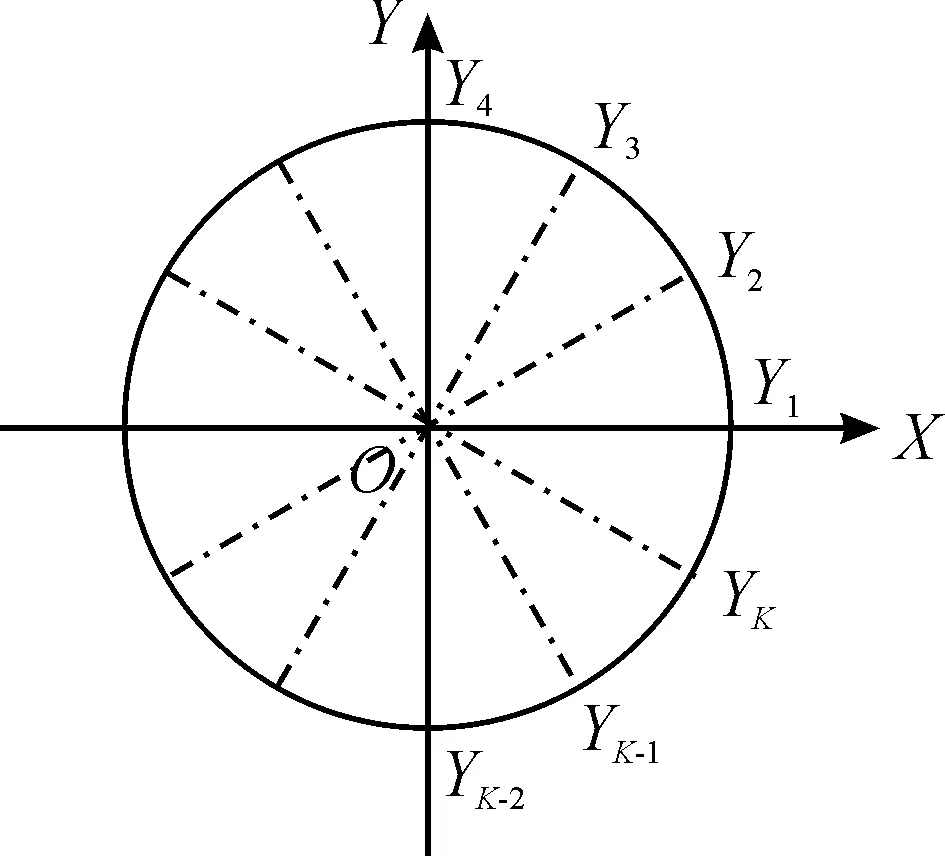
图1 周期性名义变量的量化示意图

基于图1，周期性名义变量每种取值可以量化为：

(4)

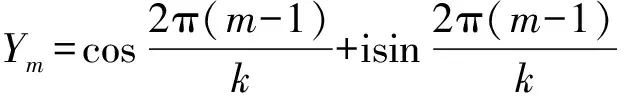
(5)

初始距离矩阵为：

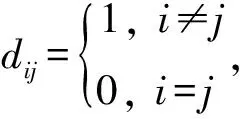
D(2)是一个主对角线元素为0，其余元素为1的对称矩阵。

若按照式(3)将周期性名义变量Y的k种不同取值Y1,Y2,…,Yk依次量化为1,2,3,…,k，那么按照距离公式计算可得观测之间的距离为dij=|i-j|,其中i=1,2,…,k,j=1,2,…,k。进而可得周期性名义变量观测之间的距离矩阵为：

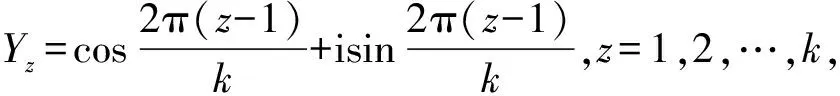
其中m=1,2,…,k,n=1,2,…,k，进而可得周期性名义变量观测之间的距离矩阵为：

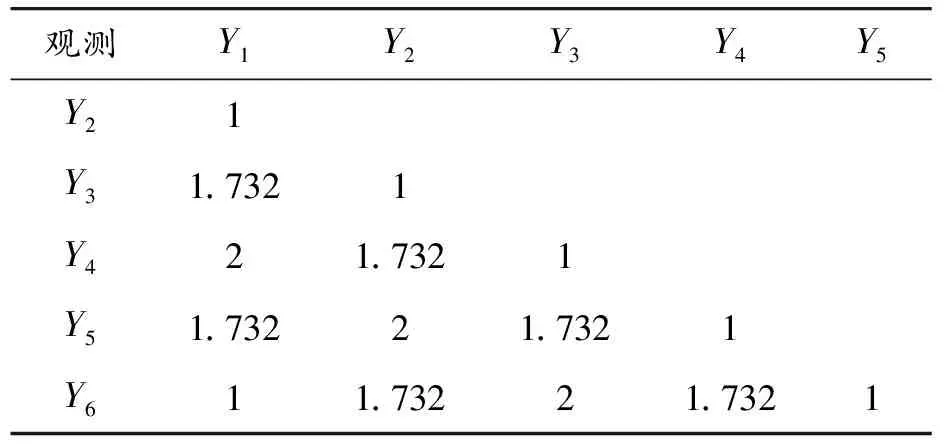
表1 依据式(5)所得观测之间的距离矩阵

从表1可以看出，d13、d24、d35、d46的值均为1.732。若按照式(2)计算，它们之间的距离都为1。这是因为式(2)采用文献[17]中的if-else语句来计算观测之间的距离，例如，if(Y1=Y2) thend12=0,elsed12=1。该方法只对属性变量的观测值是否相同做判断，忽略属性变量的不同观测值之间相似性的差异，用来计算具有周期性的名义变量观测之间的距离并不合理。表1中，d13和d15的值均为1.732，然而按照式(3)来计算，d13=2，d15=4。这是因为式(3)所述方法将Y1,Y2,…,Y5,Y6分别量化为1,2,3,4,5,6，故用来计算具有周期性的名义变量观测值之间的距离是不合理的。

1.1.3混合型数据样品之间的距离

假设观测数据矩阵X中既有由数值型变量得到的观测,又有由属性变量得到的观测，指标个数为v，其中数值型指标个数为p，属性指标个数为q。任取X中的2个样品Xi=(xi1,…,xip,xi(p+1),…,xi(p+q))和Xj=(xj1,…,xjp,xj(p+1),…,xj(p+q))，结合距离式(1)、(2)、(3)和(5)，定义出具有周期性名义变量的混合型数据观测的距离计算公式，它们之间的距离如下：

(6)

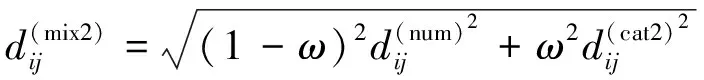
(7)

(8)

基于式(7)，初始距离矩阵为

基于式(8)，初始距离矩阵为

说明2在距离式(6)—(8)中，假设取ω=0，则式(6)—(8)均为式(1)。在距离公式(6)中，取ω=1，则式(6)为式(2)；距离公式(7)中，取ω=1，则式(7)为式(3)；距离公式(8)中，取ω=1，则式(8)为式(5)。式(6)—(8)是将数值型变量观测之间的距离公式(1)和属性变量观测之间的距离公式(2)、(3)和(5)进行统一，在ω取值为0或1时，混合型数据样品间的距离公式转变为纯数值型变量观测之间的距离公式或纯属性变量观测之间的距离公式。

1.2 类合并准则

对混合型数据的观测应用样品间距离公式(6)—(8)，可得初始距离矩阵D0，进而通过类间距离公式进行类间合并。在类合并过程中，确定类间距离有最短距离法、最长距离法、类平均法、重心法等。其中，最短距离法和最长距离法仅用距离最短和距离最长的2个样品之间的距离来代表类间距离，由于不能充分利用样品之间的信息，类间距离容易被异常值严重扭曲。考虑到物理学中物体可以其重心来指代，故将类与类之间的距离定义为两类重心之间的距离。重心法在处理异常值方面相比最短距离法和最长距离法更加稳健，不容易被异常值干扰，但如何计算混合型数据类的重心是复杂和困难的。

相较于最短距离法、最长距离法和重心法，类平均法能较好利用所有样品之间的信息。由于避免了类重心的计算，类平均法通常被认为是一种类间距离公式。本文中主要以类平均法为依据来验证周期性名义变量观测的量化方法和新定义的距离公式的合理性。

采用do1o2表示样品o1与样品o2之间的距离，用C1,C2,…表示类。定义类CP与类Cq之间的距离Dpq为类CP中各样品与类Cq中各样品两两之间距离平方的均值再开方，即

(9)

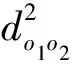
通过式(9)可以证明：在某一步将类CP与类Cq合成新的一类Cr后，Cr与某类Ck之间的距离Drk为

式中：nr和nk分别为类Cr和类Ck的样本量，且nr=np+nq。

说明3k-prototypes算法思想首先是从混合型数据集中随机挑选k个观测作为初始凝聚点，根据距离公式计算各个观测与初始凝聚点的距离，即距离矩阵。按照距离最短原则将所有的观测划分到相应的类中并更新每个类的类中心作为新的凝聚点，然后重新计算距离矩阵，对观测进行划分并更新每个类的类中心，直到误差函数达到最小。但算法迭代过程中如何更新新的类中心始终是一个难题，即数据集中的属性数据的类中心如何确定。系统聚类法可避免类中心更新的问题。由于式(2)本质上并没有将名义变量的观测进行量化，因而不能采用k-prototypes等算法进行分类，本文采用系统聚类法。

2 聚类算法

2.1 算法流程

根据式(6)—(9)编写算法。算法具体步骤为：

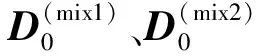
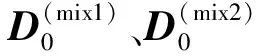
步骤3根据类间距离公式(9),计算新类Cr与其他类Ck之间的距离Drk，即

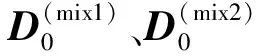
2.2 算法伪代码

算法伪代码如下：

输入：混合型数据集X;

输出：聚类结果;

Step1：for iin1：nrow(X);

Step2：forjin1：nrow(X);

Step3：sqrt(sum((X[i,]-X[j,])2));

Step4：calculate initial distance matrixD0;

Step5：end for;

Step6：end for;

Step7：while(dim(D0)>1);

Step8：forsin2：nrow(D0);

Step9：fortin1：(r-1);

Step10：if(D0[s,t]==min(D0));

Step11：doCr={Cs,Ct};

Step12：end for;

Step13：end for;

Step14：forkin1：nrow(D0);

Step15：calculate the distance ofCrandCk;

Step16：add newDrkto initial distance matrixD0;

Step17：delete rowsandt,delete colsandt;

Step18：gain transition matrixD1;

Step19：doD0=D1;

Step20：end for;

Step21：if(dim(D0)==1) break;

Step22：end;

3 实验

3.1 实验环境与数据

为了验证距离公式(8)的有效性，用式(8)在数据集Algae和Absence上进行验证，并与距离公式(1)、(6)和(7)的实验结果进行比较分析。采用R3.5.1数据分析软件编程进行实验，实验数据为带有周期性名义变量的混合型数据，均来源于UCI机器学习数据库。数据集描述见表2。

表2 数据集描述

采用Accuracy值、G-mean值作为聚类效果的评价指标,其中T1、T2、T3、T4和T5分别表示聚类后类C1、C2、C3、C4和C5中正确分类的样品数量，F1、F2、F3、F4和F5分别表示聚类后类C1、C2、C3、C4和C5中错误分类的样品数量，评价指标Accuracy和G-mean分别定义为：

(10)

(11)

3.2 Algae数据集实验结果

Algae数据集的样本量为122，变量(指标)数为11,其中数值型特征数为8，属性特征数为3。数据集共分为5类，各个类的实际样本量分别为28、21、25、23、25。以式(1)、式(6)、式(7)和距离公式(8)为依据进行分类，得到分类后的混淆矩阵如表3所示。依据各距离公式分类的Accuracy值(准确率)、G-mean值(平均准确率)、Time(s)(算法运行时间)和O(T(n))(算法时间复杂度)见表4。

表3 依据各距离公式分类后的混淆矩阵

表4 依据各距离公式分类的准确率

3.3 Absence数据集实验结果

Absence数据集的样本量为96，变量(指标)数为10,其中数值型变量数为5，属性变量数为5。数据集共分为5类，各个类的实际样本量分别为23、24、13、26、10。以式(1)、式(6)、式(7)和本文新的距离公式(8)为依据进行分类，得到分类后的混淆矩阵如表5所示。依据各距离公式分类得到的Accuracy值、G-mean值、Time(s)(算法运行时间)和O(T(n))(算法时间复杂度)见表6。

表5 依据各距离公式分类后的混淆矩阵

表6 依据各距离公式分类的准确率

3.4 实验结果对比分析

为了更直观地比较以式(1)、式(6)、式(7)和距离公式(8)为依据得到的聚类效果，直方图2显示了各距离公式分类的准确率。

图2 各距离公式分类的准确率直方图

从图2(a)和图2(b)可以看出，依据距离公式(8)在数据集Algae和Absence上进行分类得到的Accuracy值和G-mean值均优于采用式(1)、式(6)和式(7)时,验证了距离公式(8)的有效性。这种有效性来源于对混合型数据中的周期性名义变量的观测值进行合理量化，并定义出周期性名义变量的观测值之间的距离公式。另外，根据式(1)在数据集Algae和Absence上分别进行分类得到的Accuracy值和G-mean值均低于其他3种距离公式的Accuracy值和G-mean值。这是因为根据式(1)对数据集进行分类时只用到了混合数据中的数值型变量数据，并没有考虑属性变量数据，对数据集的信息利用度低。这也意味着数据集中的属性变量在聚类中重要程度高，对聚类结果有较大的影响。比较式(6)和式(8)在2个数据集上进行分类得到的Accuracy值和G-mean值可以发现，根据式(8)进行分类得到的Accuracy值和G-mean值均高于根据式(6)进行分类得到的Accuracy值和G-mean值。比较式(7)与式(8)在2个数据集上进行分类分别得到的Accuracy值和G-mean值可以发现，根据式(8)进行分类得到的Accuracy值和G-mean值高于根据式(7)进行分类得到的Accuracy值和G-mean值，这也说明将式(2)和式(3)用于计算周期性名义变量观测之间的距离是不合理的。

综上，基于新的距离公式(8)得到的聚类精度优于其他3种距离公式，验证了对周期性名义变量的观测值采用式(4)量化的合理性和新的距离公式(8)的有效性。

4 结论

对带有周期性名义变量的混合型数据中的周期性名义变量的观测值进行合理量化，以改进周期性名义变量的观测值之间相似性度量的不足。给出周期性名义变量的观测值之间的新的距离公式，有效地解决了该问题，并以此为依据对具有周期性名义变量的混合数据进行分类。各距离公式的实验结果表明所提出的新的距离公式(8)对混合型数据分类有较明显的优势。

新算法在计算海量混合型数据时存在运算速度过慢的问题，因此，研究适用于海量混合型数据的动态聚类法中新类的类中心计算，使算法更具普适性是下一步研究的方向。