埋地管道三参量粘弹性边界地震模型及其动力响应研究
2022-04-15吴静波曾祥国赵清龙
吴静波,杜 强,曾祥国,李 伟,赵清龙
(1.四川大学 建筑与环境学院,深地科学与工程教育部重点实验室, 成都 610065;2.西南油气田分公司通信与信息技术中心, 成都 610051)
埋地管道是天然气运输的主要途径,具有运量大、占地少的优点。埋地管道分布广泛,其承受的外界载荷错综复杂,国内外天然气管道事故时而发生[1-3],地震也是造成输气管道破坏的重要因素之一[4]。地震载荷作用下,埋地输气管道一旦被破坏,将严重影响能源的运输和供应,同时逸出的天然气还可能引起火灾和爆炸,造成巨大经济损失。因此,研究埋地输气管道设施在地震荷载作用下的动力响应并进行安全性评价十分必要。
地震作用时,结构瞬间承受过大的载荷,极易引发结构的失效和破坏。由于地表结构的破坏和损伤比地下结构更容易观测到,现有的研究更多集中在地震对地表结构的影响,如地面建筑物、大坝等。然而,在近些年的一些地震[5-7]中,出现了严重的地下结构破坏现象,这促使地震工程师们更多关注地下结构的设计[8-12]。在进行地震动力分析时,结构与无限域的地基存在能量交换,模型边界的处理对计算结果影响很大。Deeks等[13]和刘晶波[14-15]建立了粘弹性人工边界,在模拟结构-地基的动力响应时具有较高的精度。
本文在原有的粘弹性边界元件上串联一个弹簧元件,建立了三参量粘弹性人工边界,使用商业有限元软件ANSYS实现并验证了三参量粘弹性边界。最后,将三参量粘弹性边界应用到埋地管道的地震模型中,研究了地震波入射角和管道埋深对埋地管道动力响应的影响,为埋地输气管道的抗震设计提供了一定依据。
1 三参量粘弹性人工边界
1.1 现有的粘弹性人工边界及其缺点
如图1所示,现有地震模型使用的粘弹性人工边界普遍采用两参数Kelvin固体模型。在进行动力分析时,将管道和周边一定区域内的土壤从无限域中切取出来,并在边界的法向(图1中的Y向)和2个切向(X向和Z向)施加弹簧阻尼器系统来连接有限的管道结构和地基,使边界上满足相当于无限域的应力-位移协调条件。边界上弹簧阻尼器系统的弹簧刚度和阻尼系数的取值为[16-17]:

(1)
(2)


图1 管道结构的两参数粘弹性边界地震模型示意图
上述的两参数粘弹性人工边界考虑了对散射波能量的吸收和边界外半无限介质的弹性恢复,在土-结构相互作用模型的地震分析中得到了广泛应用。然而,这种模型存在致命的弱点,两参数粘弹性边界采用的Kelvin固体模型无法描述松弛特性[19],即不能描述岩土完整的蠕变、松弛、回复的粘弹性特性。
1.2 三参量粘弹性人工边界地震模型的建立
在同时考虑人工边界对散射波能量吸收和边界外半无限介质弹性恢复的前提下,为了能完整描述边界层的粘弹性,本文在原有的粘弹性边界元件上串联一个元件,构成了三参量固体(Kelvin-Voigt模型)模型(该模型能描述完整的蠕变、松弛、回复的粘弹性特性[19]),并使用该模型建立三参量粘弹性人工边界。
1.2.1有限地震模型法向边界等效参数的推导
将结构从无限域介质中截断,并在底部和四周的边界节点上施加三参量粘弹性边界。在边界的法向,施加如图2所示的弹簧-弹簧-阻尼器-集中质量系统。该物理系统的运动平衡方程和位移协调方程为:
(3)
(4)
式中:U为边界节点的位移;σ为位移U在人工边界处产生的应力;K1和K2分别为图2中对应位置弹簧的刚度;U1为与边界节点相邻弹簧的位移;U2为远离边界节点弹簧的位移;UC为阻尼器的位移;UM为集中质量点的位移;C为阻尼器的阻尼系数;M为集中质量。
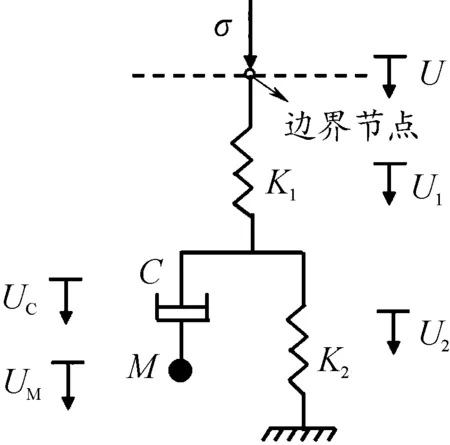
图2 边界法向的三参数粘弹性物理系统示意图
由式(3)和(4)可得边界节点应力和位移的关系:
(5)

(6)
球坐标系中,P波波阵面上法向应力与位移的关系[16]为:
(7)
式中:R为人工边界节点与散射源的距离;G为介质的剪切模量;ρ为介质的密度;cP为介质的P波波速。
对照式(6)和(7),有:
(8)
1.2.2有限地震模型切向边界等效参数的推导
对于边界的切向,直接施施加三参量固体(Kelvin-Voigt模型)模型即可,如图3。
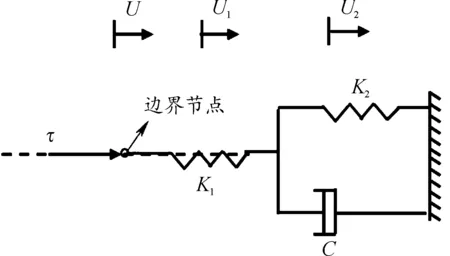
图3 边界切向的三参数粘弹性物理系统
Kelvin-Voigt模型应力与位移的关系为:
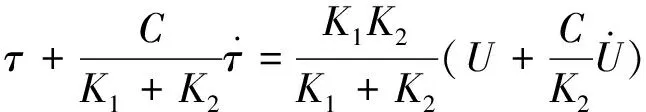
(9)


(10)
球坐标系中,S波波阵面上切向应力与位移的关系[16]为:
(11)
式中:cS为介质的S波波速。
对比式(10)和(11),可得:
(12)
1.2.3数值模拟技术中的参数设置
图2中的质量M和阻尼器组成一个不稳定的系统,为了方便计算和处理,数值模拟中将质量M忽略,并将阻尼器固定。三参量粘弹性边界可以通过有限元软件ANSYS的Combin14单元实现。具体实现方法为:在需要施加人工边界的截面上向法向和切向均延伸两层Combin14单元,其中一层单元设置同时设置弹簧刚度和阻尼系数,另一层单元只设置弹簧刚度。法向的弹簧刚度KN1、KN2、阻尼系数CN和切向的弹簧刚度KT1、KT2、阻尼系数CT分别为:
(13)
(14)
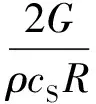
1.2.4三参数粘弹性边界的地震输入方式
数值模拟时,将地震波加速度转换为人工粘弹性边界上的等效节点载荷来实现地震波的输入。在边界上应力和位移满足图4所示的关系:
(15)
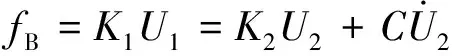
(16)
式中:FB为施加在人工边界上的等效节点载荷;fB为弹簧阻尼器系统与人工边界连接处的内力;U为地震波在人工边界处产生的位移;σ为位移U在人工边界处产生的应力;U1为与边界点相邻弹簧的位移;U2为远离边界点弹簧的位移,可以由位移U求得。
于是,人工粘弹性边界上的等效节点载荷FB为:
(17)

图4 三参量人工粘弹性边界上的等效载荷
1.3三参量固体(Kelvin-Voigt模型)粘弹性人工边界的验证
本文使用ANSYS的combin14单元,并用ANSYS命令流语言编写程序实现了三参量粘弹性人工边界及其对应的地震波输入。然后,使用有限元软件ANSYS模拟了三维Lamb表面源问题和P波斜入射的波动问题,得到的位移数值解与(近似)理论解吻合得较好,验证了三参量粘弹性边界的有效性。
1.3.1三维Lamb表面源问题
三维表面源问题的数值模型如图5所示,模型范围为X向-60~60 m,Y向-60~0 m,Z向-60~60 m。介质为均匀线弹性材料,其剪切模量为500 MPa,泊松比为0.25,密度为2 000 kg/m3。模型的上表面为自由面,底部和4个侧面考虑了三参量粘弹性边界(如图5,在模型边界节点的法向和2个切向共施加3组3个元件的弹簧阻尼器系统)、两参量粘弹性边界与远置边界(作为近似解)。 三参量粘弹性边界的n取10 000,法向、切向边界参数取4/3和2/3;两参量边界的法向、切向边界参数取4/3和2/3;远置边界将原有边界向外延伸了500 m(在计算时间 1 s内,反射波未传回计算区域)。在坐标原点施加动力载荷F(t),并观测点A(30,-30,0)、B(30,-30,30)位移时程。动力载荷F(t) 的单位为N,表达式为:
(18)

图5 Lamb表面源算例模型及三参量边界示意图
图6、7分别为A点和B点的位移时程曲线。从图6、7可以看出,三参量粘弹性边界的位移时程和两参数边界的位移时程基本重合,且均和远置边界的近似解吻合得较好,证明了本文使用的三参量粘弹性人工边界的可行性。

图6 不同边界下A点的位移时程曲线
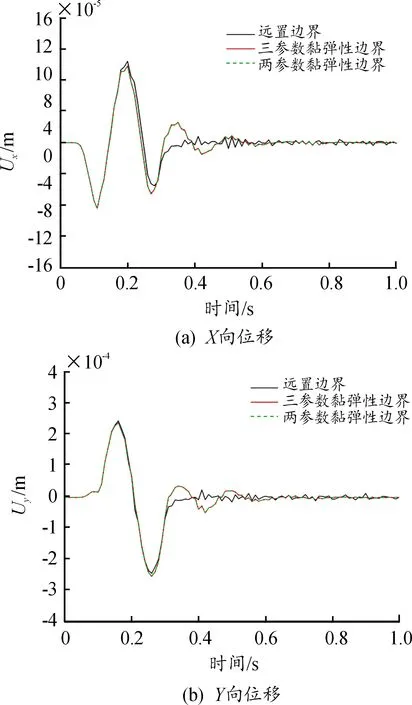
图7 不同边界下B点的位移时程曲线
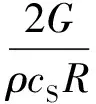

图8 不同n值下A点的Y向位移时程曲线
1.3.2P波斜入射的波动问题
模型在几何和边界上与Lamb表面源问题相同。介质的剪切模量为5.292 GPa,泊松比为0.25,密度为2 700 kg/m3。模拟P波从底部的入射点C(-60,60,-60) 斜入射,入射波与Y轴夹角为60°,入射波与反射波平面和X轴的夹角为45°。入射波在C点引起的位移时程为:

(19)
图9为观测点O(0,0,0) 位移时程的解析解和使用粘弹性人工边界的数值解。如图9(a)和图9(b)所示,观测点O在X、Y方向位移的数值解均和解析解吻合较好,进一步说明了本文使用的三参数粘弹性人工边界的有效性。
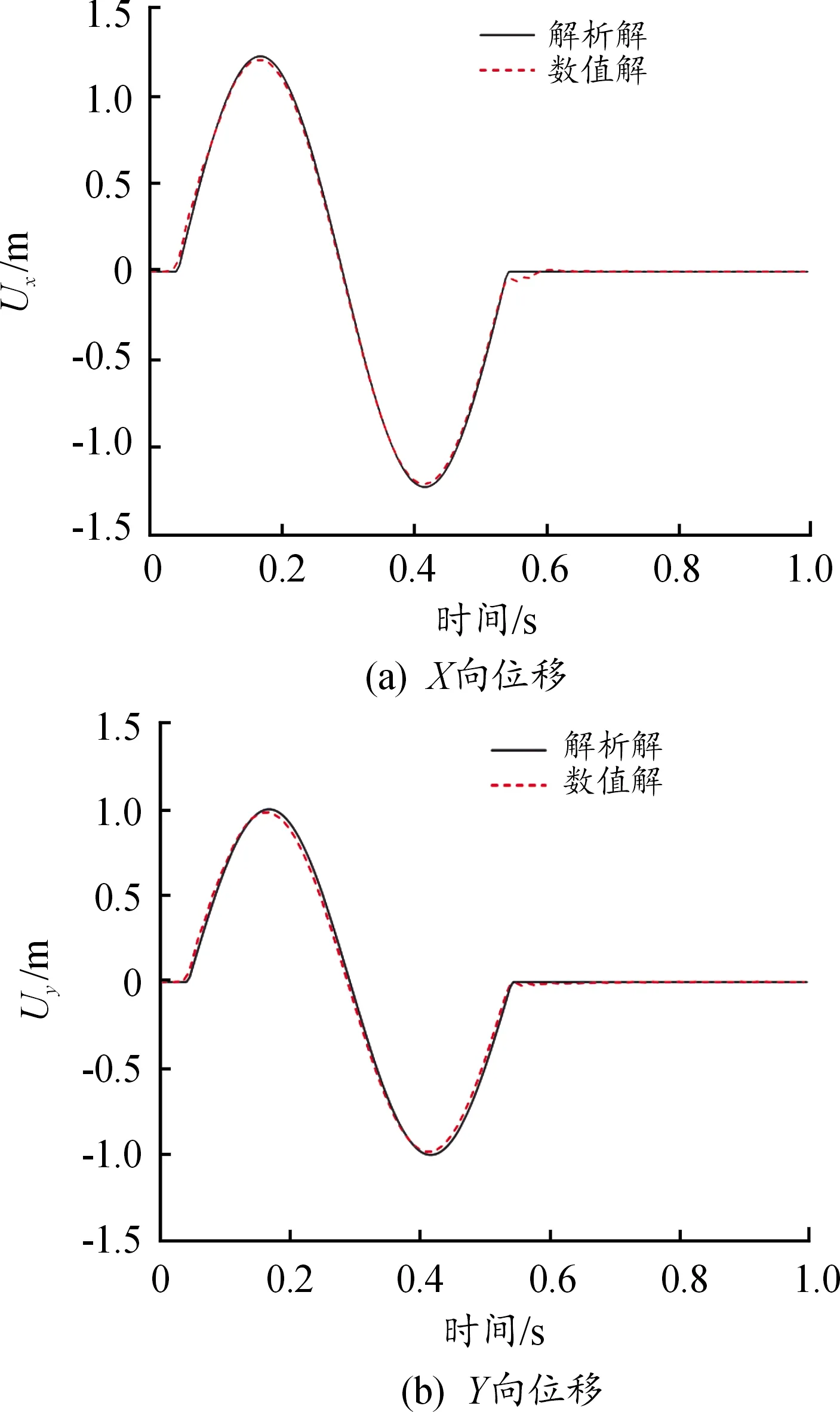
图9 观测点O的位移时程
2 埋地输气管道有限元模型建立
2.1 管线钢和土壤的材料参数
管道的材料为X80管线钢[10],其弹性模量E为210 GPa,泊松比ν为0.3,密度ρ为7 900 kg/m3。土体使用Drucker-Prager模型,其材料参数见表1[18]。

表1 土体的材料参数
2.2 埋地管道的有限元模型
管道的有限元模型取长度15 m,外径121.9 cm,壁厚为1.8 cm,埋深(管道中心与地面的距离)为3 m;土体取6 m×6 m×15 m的块体(Y向为竖直方向;Z向为管道轴向,长度15 m),其截面的几何模型如图10所示。管道的有限元模型如图11所示,管道和土体均使用Solid186单元,管道与土体的接触通过定义接触对实现。模型是在很长的管线中截取的一截,所以在管道轴向的2个边界面上使用对称边界;在模型的底面和2个侧面施加三参量粘弹性边界;模型上表面为自由面。

图10 埋地管道的几何模型及监测点示意图

图11 埋地管道的有限元模型及边界
3 地震载荷作用下管道的动态响应
3.1 地震波在模型边界输入
埋地管道位于四川江油,根据抗震设计规范,该地区的抗震设防烈度为7°,设计基本地震加速度值为0.15g,设计地震分组为`第二组,建筑场地为Ⅱ类。本文选择罕遇地震来进行抗震设计,由表2可知,输入地震加速度的最大值为310 cm/s2。本文使用EI Centro波作为输入地震波,时长为30 s,时间间隔0.02 s,其加速度时程曲线如图12所示。地震波的输入通过式(17)将地震波转化为等效节点载荷实现。

表2 时程分析时输入地震加速度的最大值 (cm/s2)
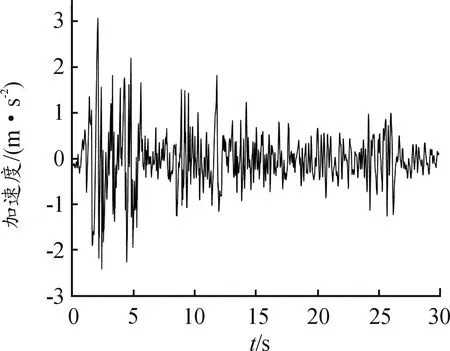
图12 调整最大加速度后的EI Centro波
3.2 地震波入射角对管道动态响应的影响
由于震源具有很强的不确定性,地震波传到埋地管道的输入角也随之不同。将地震波沿水平和垂直方向分成2个分量,不改变地震波加速度大小,通过调整2个分量的比值,可以得到不同的地震波输入角度。数值模拟中,输入角度分别为0°、15°、30°、45°、60°、75°和90°。
选取模型中部截面处管道内壁的底部节点(1号点,节点编号31313)、顶部节点(2号点,节点编号27684)、右端节点(3号点,节点编号27655)和左端节点(4号点,节点编号29513)作为监测点,并分析4个节点在不同入射角下的位移和应力响应。4个节点的具体位置如图10所示。
3.2.1不同入射角的位移响应
图13依次给出了入射角为0°、45°、90°时,4个节点的合位移时程曲线。受地震波的作用,4个节点合位移时程曲线的变化趋势相同,在幅值上有一定的差异。图13(a),入射角为0°时,管道底部节点的位移幅值最大;底部的位移幅值最小;图13(b),入射角增大到45°时,底部和右端节点、顶部和左端节点的位移幅值分别保持一致,且底部节点和右端节点的位移较大;图13(c),入射角为90°时,各节点的位移时程曲线几乎重合,管道的位移响应呈现出整体一致性。

图13 不同入射角下各监测点的合位移响应曲线
图14给出了不同入射角下,管道底部节点的合位移时响应曲线。可以看出,随着入射角的增大,位移响应也越大;8.62 s,位移达到峰值时,不同入射角的位移差异也达到最大;0°入射角的最大位移为0.61 m,而90°入射角的最大位移达0.131 m。
综上,管道受地震作用时,管道底部区域的位移响应最大,是管道抗震设计中应着重关注的位置;地震波的入射角越大,管道的位移响应越大,越容易在地震中受损。

图14 不同入射角下管道底部节点的位移时程曲线
3.2.2不同入射角的应力响应
本文选取Von Mises等效应力分析管道的动态应力响应。选取管道中部截面内壁上的所有节点,并获取了这些节点在不同入射角地震波作用过程中的最大等效应力。图15给出了不同输入角对应的最大等效应力环管道内壁的分布曲线,同时给出了环管道内壁的初始应力分布作为参照。图15中,极坐标的0°对应图10中的管道右侧的27655号节点;90°对应管道顶部的27684节点;180°对应管道左端的29513号节点;270°对应管道底部的31313号节点。如图15所示,初始应力呈椭圆形分布,底部和顶部初始应力较大;入射角从0°~45°时,最大等效应力的峰值不断增大,峰值的位置朝逆时针方向发生偏移;入射角从 45°~90°,最大等效应力的峰值逐渐减小,峰值出现的位置继续向逆时针方向偏移。

图15 不同入射角的最大等效应力环向分布图
为了说明最大等效应力的值和位置随入射角的变化关系,图16给出了整个管道在地震过程中的最大等效应力和最大等效应力增量(最大等效应力减去初始时刻的应力)与入射角关系曲线;表3是0°到90°入射角所对应的最大等效应力和最大等效应力增量的位置。

表3 不同入射角管道内最大等效应力和等效应力增量的位置 (°)
如图16,最大等效应力和应力增量随地震波入射角的变化趋势相同,均先增大后减小,最后趋于平稳;最大等效应力和应力增量均在45°时达到最大,值分别为364 MPa和54.4 MPa。如表4,同一入射角的最大等效应力和最大等效应力增量所处的位置基本一致,为同一节点或相邻节点(管道内壁共有80个节点,相邻节点位置相差4.5°);管道内最大等效应力的位置从入射角0°到90°依次为243°、247.5°、247.5°、247.5°、247.5°、265.5°、270°。

图16 不同入射角下,管道内的最大等效应力及增量曲线
综上,随着入射角从0°增大到90°,地震过程中最危险的位置(等效应力最大)由243°(管道底部偏左27°)逐渐转移到270°(管道正底部),危险位置的等效应力先增大后减小;地震波0°入射的最大等效应力为332 MPa,对管道强度的威胁最小;地震波45°入射对管道的强度威胁最大,此时的最大等效应力值为364 MPa,位置位于管道内壁247.5°处。
3.3 埋深对管道动态响应的影响
在管道壁厚均为18 mm,地震波输入角均为90°的情况下,采用管道埋深为3、3.5、4、4.5、5 m研究埋深对管道地震动力响应的影响。由上一节知,地震波90°入射时,管道底部31313号节点的应力和位移响应最大,所以本节着重分析管道底部。
3.3.1不埋深管道的动态位移响应
埋深不同时,31313号节点的Y向位移时程如图17所示。由图17知,埋深越大,管道底部的位移响应越小。
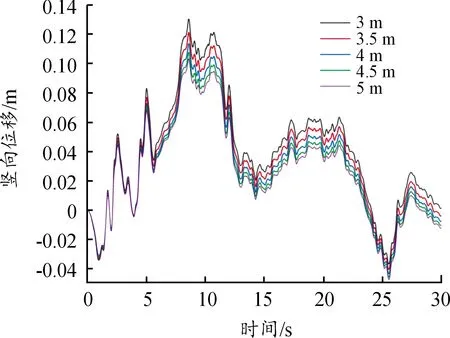
图17 不同埋深管道31313号节点的Y向位移时程曲线
图18显示了31313号节点的最大Y向位移与管道埋深的关系。埋深为3 m时,31313号节点的最大位移为0.131 m;埋深增加到5 m时,最大位移减小至0.103 8 m,减小了20.8%。最大位移在相邻埋深的减小量和减小百分比见表4。埋深从3 m到3.5 m时,管道的位移减小量最大,值为9.02 mm,位移减小的百分比也最大,值为6.88%;随着埋深继续增加,位移减小量和减小的百分比均变小;4.5~5 m时,位移减小量仅有4.55 mm,减小位移的效果为3~3.5 m的一半。
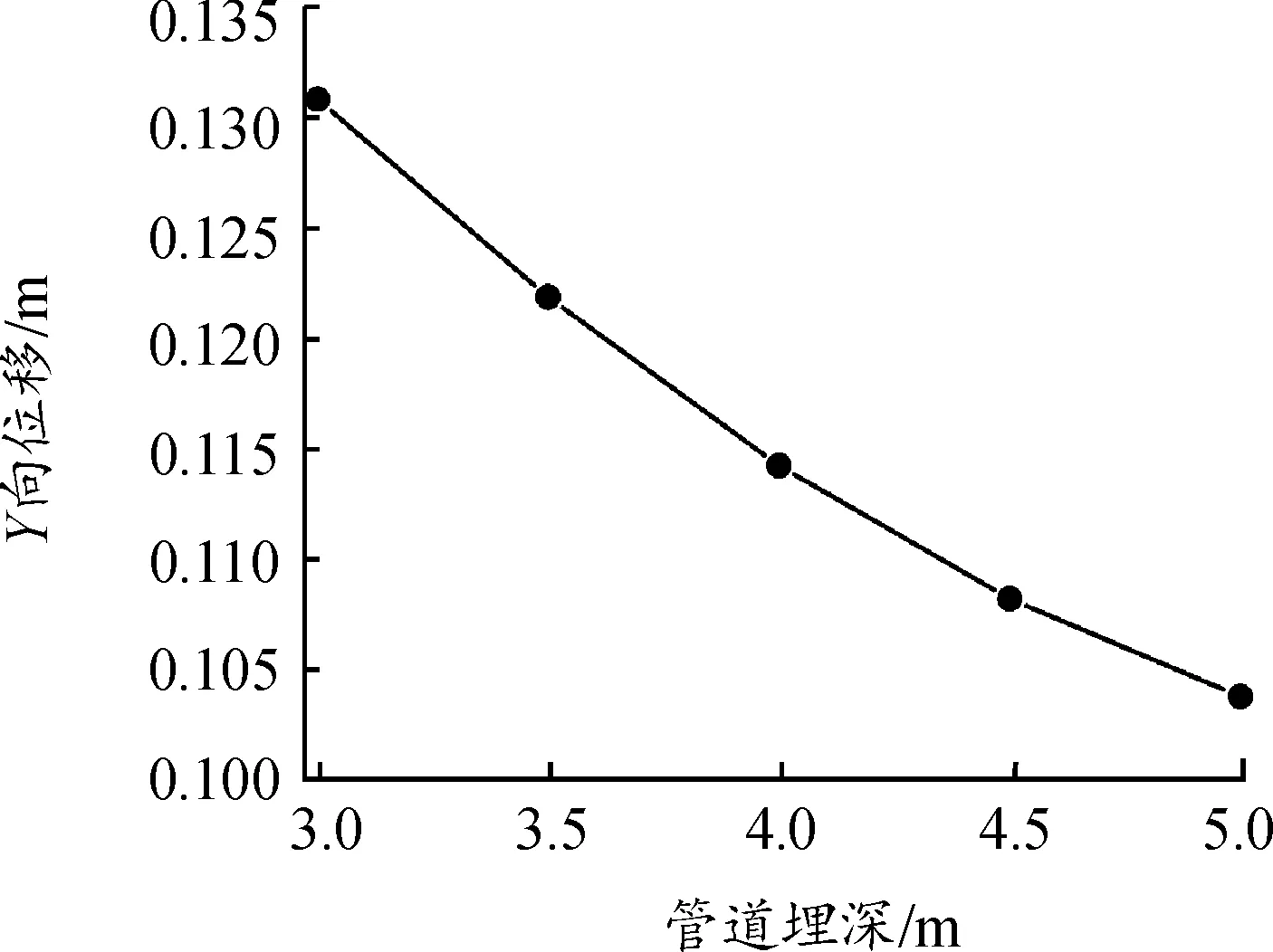
图18 不同埋深的最大Y向位移

表4 相邻埋深31313号节点的最大位移减小量和减小百分比
由图17、18和表4可得出,增大管道的埋深可以减小管道的位移响应,增强管道的抗震能力,但位移减小幅度变弱。
3.3.2不同埋深管道的动态应力响应
31313号节点在不同埋深下的等效应力时程曲线如图19所示。埋深越大,管道的动态应力响应越大,最大等效应力也最大,越容易在地震中被破坏。
为了更详细地描述埋深对管道应力响应的影响,图19给出了管道的最大等效应力与埋深的关系,并在表5中给出了相邻埋深的应力增量和应力增量百分比。由图20知,随着管道埋深的增大,最大等效应力呈线性增长,埋深从3 m增至 5 m时,最大等效应力增加了35.5 MPa,平均增长率为2.57%。由表5知,3.5~4 m时,最大应力的增量有最大值10.62 MPa,增加的百分比为3.01%;4.5~5 m时,增大应力的增量有最小值7.79 MPa,增量百分比为2.06%;随着埋深的增加,管道最大等效应力也平稳增加。

图19 不同埋深管道31313号节点的等效应力时程曲线
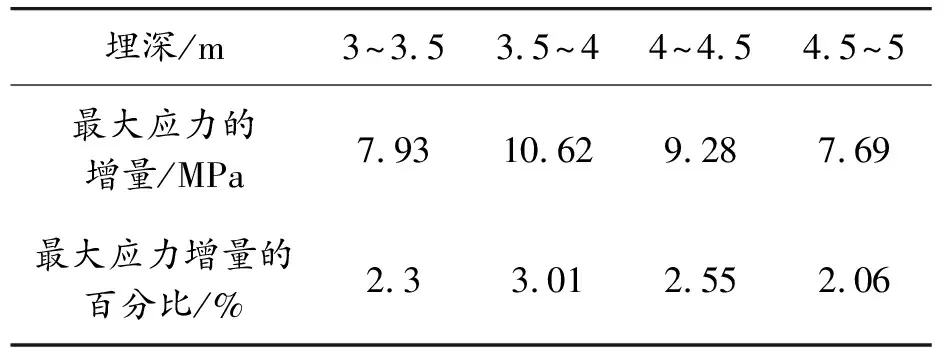
表5 相邻埋深的最大等效应力量和增量百分比

图20 不同埋深的最大等效应力曲线
由于管道的应力响应和位移响应随埋深的变化趋势相反,所以在进行埋地管道的抗震设计时,需要综合考虑最大等效应力和最大位移与埋深的关系。在管道强度足够的前提下,适当增大埋深有利于提升埋地管道的抗震性能。
4 结论
1) 本文建立的三参量粘弹性边界与传统两参量粘弹性边界具有同等的精度,在描述边界层的粘弹性时优于传统的粘弹性边界。
2) 对于管道内壁的底部、顶部、左右端4个特殊位置,底部的位移响应最大且地震波入射角越大,位移响应最大;对于整个管道,地震波45°入射时,管道的应力响应最大,对管道的强度威胁最大,危险点位于管道内壁247.5°处。
3) 地震波90°入射时,管道埋深越大,管道的位移响应越小,应力响应越大;在管道强度足够的前提下,适当增大埋深有利于提升埋地管道的抗震性能。
4) 对结构-地基相互作用系统(如埋地输气管道)进行动力分析时,边界是影响计算精度的重要因素。本文提出的三参量粘弹性边界在具有高精度的同时又能完全描述边界层的粘弹性,提供的埋地管道地震分析方法和数据对埋地输气管道的抗震设计、施工与安全运营具有参考价值。
