玻璃熔窑蓄热室外墙结构参数优化研究

宋李俊，唐永晟

(重庆理工大学 机械工程学院， 重庆 400054)

我国玻璃行业年能耗约800万标煤，平均单耗为7 800 kJ/kg(1 863 kcal/kg)，比国际平均水平高20%，其中玻璃熔窑能耗占企业总能耗的80%以上[1-3]。蓄热室是玻璃熔窑的重要组成部分，其利用格子体回收高温烟气热量并预热助燃空气和燃料，提高熔化温度并节省燃料，是玻璃生产中重要的节能设备。提高蓄热室的蓄热效率是节能减排的重要途径，也是在玻璃生产中降低能耗的研究热点。

许多学者针对蓄热室结构和蓄热室热效能进行了研究。邬永国等[4]以热平衡原理建立了蓄热室温度场数学模型，通过模型分析求解得出蓄热室的结构设计中应尽量保持气流分布均匀性，否则会降低格子砖利用率，降低热效能。乐军等[5]通过建立蓄热室优化设计模型，给出总传热量最大时，蓄热室的换热面积比和烟气流量分配比的最佳值，以及最佳值下的蓄热室外墙结构参数(如格子体长、宽、高)等。黄雪丹等[6]建立了蜂窝陶瓷蓄热室加热期和冷却期的传热数学模型，选择蓄热室外墙结构参数与换向时间作为变量，综合评价温度效率、热回收率和成本价格的目标函数，进而对蜂窝陶瓷蓄热室进行遗传优化设计。刘颖等[7]在多孔介质的基础上建立蓄热室数值模型。通过该模型优化蓄热室墙体结构形状，可提高蓄热室内水平截面温度分布的均匀性。杨海东等[8]建立了马蹄焰玻璃蓄热室的数值模型和效率模型，利用CFD技术进行仿真模拟，研究表明，减小助燃空气进口速度、格子体孔隙率、格子砖当量直径，有利于增大空气与格子体的传热量，提高蓄热室的性能。

根据以上研究可知，影响蓄热室的热效能的因素众多，但蓄热室外墙结构决定了蓄热室内格子体的蓄热面积及高温废气在蓄热室内的流动，因而优化蓄热室外墙结构，能够有效提高蓄热室热效能。针对蓄热室热效能的研究，多采用数值模拟的方式进行，为了简化高温废气在蓄热室内的流动与传热，对蓄热室内格子体部分采用多孔介质模型进行替代，并且多采用热平衡状态进行仿真分析。

传统结构优化多采取实验研究方法。通过建立等比或缩小实验模型进行实验，能够得到良好的实验结果。曲祖源等[9-10]遵循相似原理，按1∶10的比例建造了一座有机玻璃蓄热室物理模型，进行了一系列实验，主要研究了蓄热室的高、底部结构等对蓄热室内气流分布的均匀性与蓄热室热回收性能的影响。实验方法的局限在于无法完全复原实际模型，而且成本相对于理论计算和计算机模型更高。响应面法是近年逐渐兴起的一种优化方法，其利用函数关系来展现变量参数对结果的影响。张永学等[11]应用响应面法和数值模拟，对蓄热式加热炉结构参数与辐射管内NO浓度的影响进行研究，并得到最优结构参数。

本文以FY公司500 t/d浮法玻璃生产线的蓄热室为研究对象，提出一种基于树突网络的响应面模型，利用响应面法构建蓄热室的热效能与蓄热室外墙结构参数的多项式函数，响应面法常用二次多项式序列回归、插值回归等算法拟合变量与目标函数，但本文采用新的回归算法——树突网络回归分析响应值与变量参数的函数关系，通过非支配遗传算法NSGAⅢ求得最优蓄热室外墙结构参数。

1 玻璃熔窑蓄热室数值模型的构建

1.1 蓄热室物理模型及工作过程

以FY公司浮法玻璃生产的玻璃熔窑蓄热室为研究对象，玻璃熔窑蓄热室如图1所示。FY公司浮法玻璃熔窑蓄热室采用分隔式布局，蓄热室被分为若干形状相同的小室，单个小室外墙长3 840 mm，宽5 850 mm，高12 467 mm，构成小炉部分外墙长960 mm，宽1 390 mm，外墙厚度 680 mm。蓄热室内的格子体是由一块块格子砖按照一定的排列方式堆叠而成，格子体中孔隙众多，建立真实的几何模型会增加Fluent求解时的计算负担，故采用多孔介质模型简化求解模型，加快求解速度。

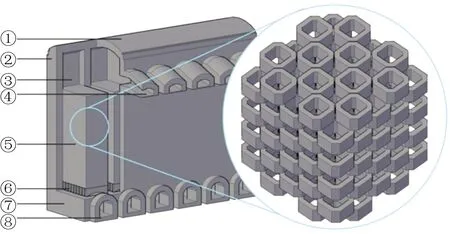
①碹顶；②外墙；③顶室；④小炉；⑤格子体；⑥炉条碹；⑦底室；⑧烟道

蓄热室是一个余热回收设备，在一个周期内分为加热和冷却2个时期。蓄热室的工作过程主要是助燃空气进入上一个周期被烟气加热的蓄热室，蓄热室里的格子体将存储的热量传递给助燃空气，然后助燃空气进入燃烧空间与燃料混合燃烧，又产生大量烟气进入另一侧的蓄热室，该过程称为冷却期。提高助燃空气的温度的目的是为了提高燃料燃烧温度，从而提高熔化率和热利用效率，节约能源。而进入另一侧蓄热室的烟气，将热量存储在具有蓄热特性的格子体中，用于加热下一个周期的助燃空气，然后从烟道中流出，该过程称为加热期。加热期和冷却期为一个周期，燃烧周期的持续时长一般在20～30 min。需要几个运行周期才能达到热平衡。蓄热室外墙结构决定了高温废气在蓄热室内的流动路径，同时影响着蓄热室内气体流动的均匀性，不均匀的气体流动会减小蓄热面积，降低蓄热效率。

1.2 数值模型

建立数学模型之前作出如下假设：废气与助燃空气均为不可压缩流体；模型的入口具有恒定流速及温度；格子体、废气、助燃空气的热力学性能恒定，且废气与格子体不发生化学反应，忽略辐射传热和热损失；蓄热室与外界隔热。

根据以上条件和质量、动量、能量守恒原理，蓄热室的数学模型如下。其中连续方程和动量方程为：

(1)

(2)

能量方程和固体区域的导热方程为：

(3)

(4)

式中：ρ、ρs为气体密度和固体密度，kg/m3；μ为湍流粘度，kg/(m·s)；σH为普朗特数；λ、λs为气体导热系数和固体导热系数，W/(m·K)；cp、cs为气体和固体比热，J/(kg·k)。

蓄热室中的格子体具有均匀孔隙，可以通过多孔介质简化模型，其模型与实际模型的不同在于多孔区域提供一个与速度相关的动量源项，表达式如下：

(5)

蓄热室开始蓄热时，废气和助燃空气与格子体在单个周期内换热时无法达到热平衡，因此多空区域内固体与流体处于局部非热平衡，多孔介质模型的固体区域与流体区域的能量方程为：

(6)

▽·(-θfkf▽Tf)

(7)

式中：θs、θf为固体与气体的孔隙率；Ts、Tf为固体与气体的温度，K；h为传热系数，W/(m3·K)。

1.3 数值模拟模型的验证

本文使用商业软件ANSYS-Fluent 19.0进行数值求解。激活能量模型及标准k-ε模型，蓄热室进口为速度进口，蓄热室出口为压力出口，多孔介质区域采用非热平衡。设定初始条件：加热期，烟气入口温度为1 710 K，烟气入口速度为11.5 m/s，蓄热室内的空气和多孔介质区域初始温度为 300 K。冷却期，助燃空气初始温度为300 K，蓄热室内和多孔介质区域的温度为加热期后的温度，助燃空气速度为3.2 m/s。加热期与冷却期周期时长30 min，时间步长为3 s，总时间步为600步，每个时间步迭代15步，使用Coupled算法进行求解。蓄热室墙体材料物性参数见表1。

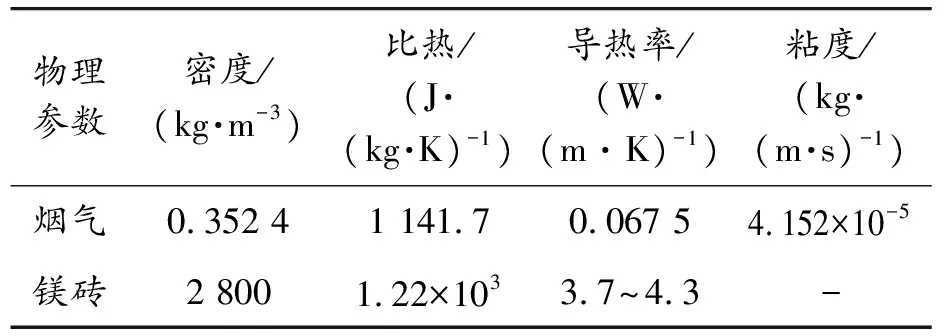
表1 烟气与墙体材料物性参数

在模型求解前，为排除网格对计算的影响，需要进行网格无关性验证。表2是网格为9、19、53、133万时，加热期烟道出口处的温度计算结果。网格数19万时，对比网格数9、53和133万的加热期出口温度，其温度误差为2.4%、0.05%和0.14%，其结果与网格数为53与133万时误差不超过1%，故认为网格数为19万时计算结果是精确的。

表2 多孔模型的出口温度

通过对蓄热室不同高度的温度传感器采集的废气温度与数值模拟下不同高度、温度的计算平均值进行对比，如表3，可以看出，数值模型的温度平均误差为4.2%，各高度下实际温度与数值模型的计算温度误差在10%以内，证明了数值模型的可靠性。

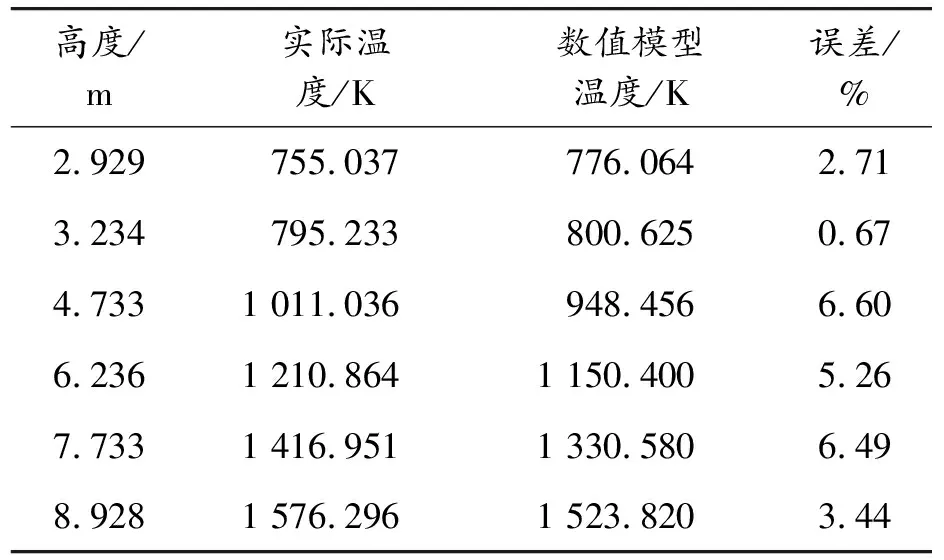
表3 截面平均温度验证

2 基于响应面法的蓄热室外墙结构参数优化模型

2.1 蓄热室热效率及出口温度

响应面法(response surface methodology，RSM)是一种解决多变量问题的方法，它通过利用试验设计的方法，实验或仿真得到一定数据，再采用回归算法构建响应值Yi和变量因素Xi的函数关系，最后通过求解回归方程的最优解寻找最优方案。

本文的响应值Yi分别为蓄热室加热期出口温度与蓄热室热效率，Yi代表加热期出口温度，蓄热室出口温度降低才能保存更多热量。在蓄热室内，能量的传递方式为对流传热，高温烟气冷却可用牛顿冷却定律来表达，即：

Q=h·A(tw-t)

(8)

式中：Q为通过传热面积的热流量，取气固交界面处传热速率，W；A为传热面积，取气固交界面处面积，m2；h为对流传热系数，W/(m2·K)；tw为传热壁面温度，取气固交界面平均温度，K；t为流体温度，取通道内流体平均温度，K。

蓄热室出口温度可由式(8)变形得到：

(9)

蓄热室热效率也叫热回收效率，是助燃空气从格子体得到的热量与废气进入蓄热室留下的热量之比，热效率是衡量蓄热室的一项重要技术性能指标，其计算公式为：

(10)

式中：η代表蓄热室热效率；Vc、Vh为通过蓄热室助燃空气与废气，Nm3/s；Tci、Tco、Thi为助燃空气进出蓄热室的温度以及废气进入蓄热室的温度，K。假定助燃空气和废气的流量是一定的，蓄热室的换热效率可以认为只与换热前后流体的温度有关。可以简化为：

(11)

2.2 响应面试验设计

响应面法第一步是试验设计，数值模拟可以得到建立响应值与变量参数间多项式的数据。本文的变量因素Xi为蓄热室外墙的高宽比x1，外墙的长宽比x2，小炉的长宽比x3。根据中心组合设计原理，本文设计了3因素5水平共25个试验点的响应面分析试验。其中22个为析因子，3个为零点。零点试验用于估计试验误差。试验设计表及模拟结果见表4。

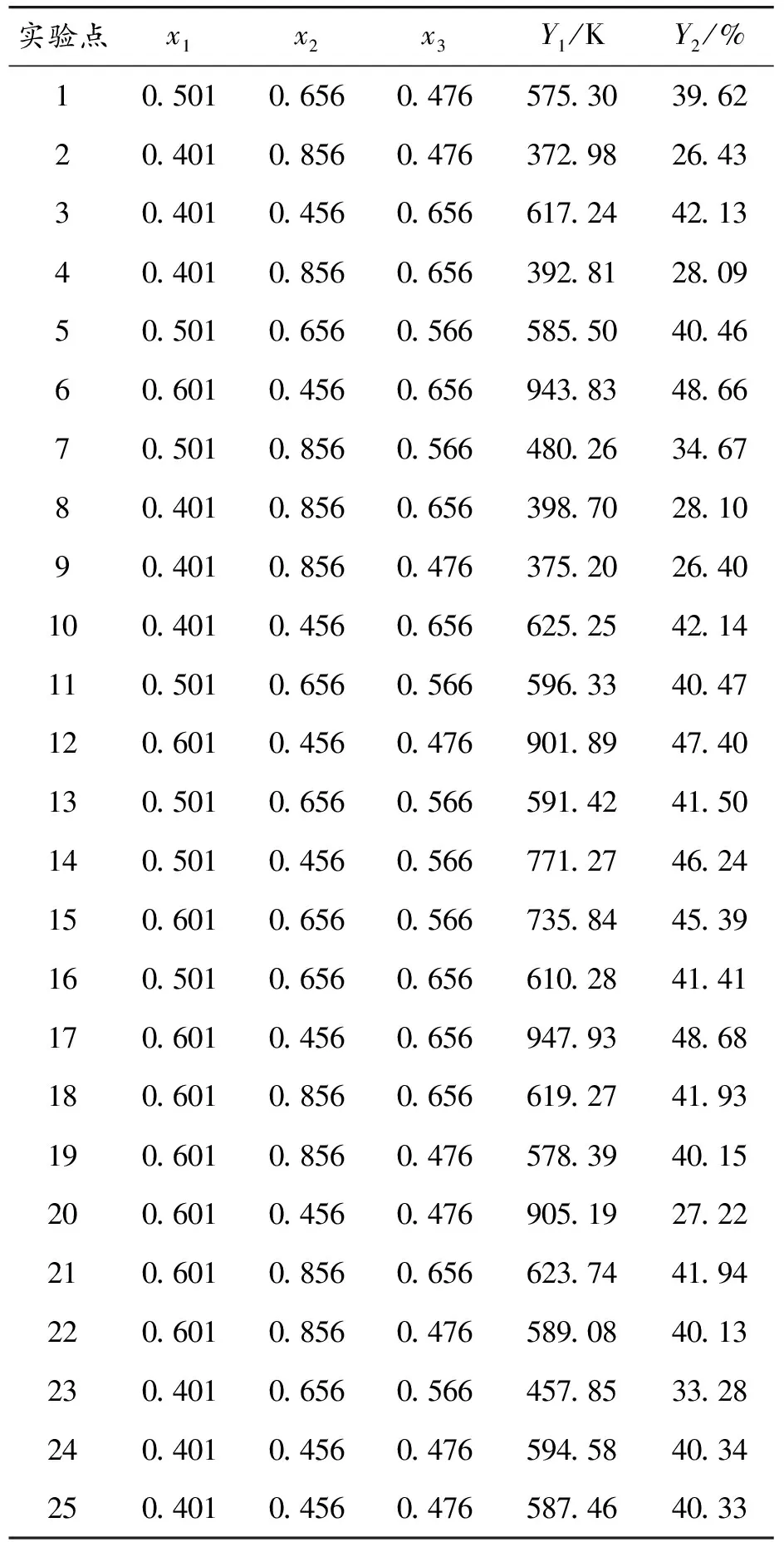
表4 中心组合设计表及模拟结果

2.3 基于树突网络的响应值与变量参数的函数拟合

1) 树突网络

响应面法中常用的函数拟合方法有二次多项式序列回归、插值回归等，本文采用一种新的算法——树突网络，结合响应面法进行变量与响应值之间的关系拟合。树突网络(dendrite net)是一种新的基本机器学习算法，拥有更好的泛化能力，在训练损失更高的情况下，树突网络在分类问题上表现出更高的准确性[12]。

树突模块可以表达为：

Al=Wl,l-1Al-1∘X

(12)

式中：Al-1和Al是模块内上一层到下一层的输入和输出；X表示DD的初始输入；Wl,l-1为模块内上一层到下一层的权重矩阵；“∘ ”表示哈达玛积。

树突网络是由DD模块共同构成，树突模型如图2所示，用以下公式表示树突网络：

Y=WL,L-1[…Wl,l-1(…W21(W10X∘X)∘

X…)∘X…],L∈N+

(13)

式中：X和Y表示输入集和输出集；Wl，l-1是从第l-1个模块到第l个模块的权重矩阵，并且最后一个模块是线性的，L表示模块的数量。树突网络的计算仅包含矩阵乘法和哈达玛积，而且哈达玛积的计算复杂度明显低于非线性函数。

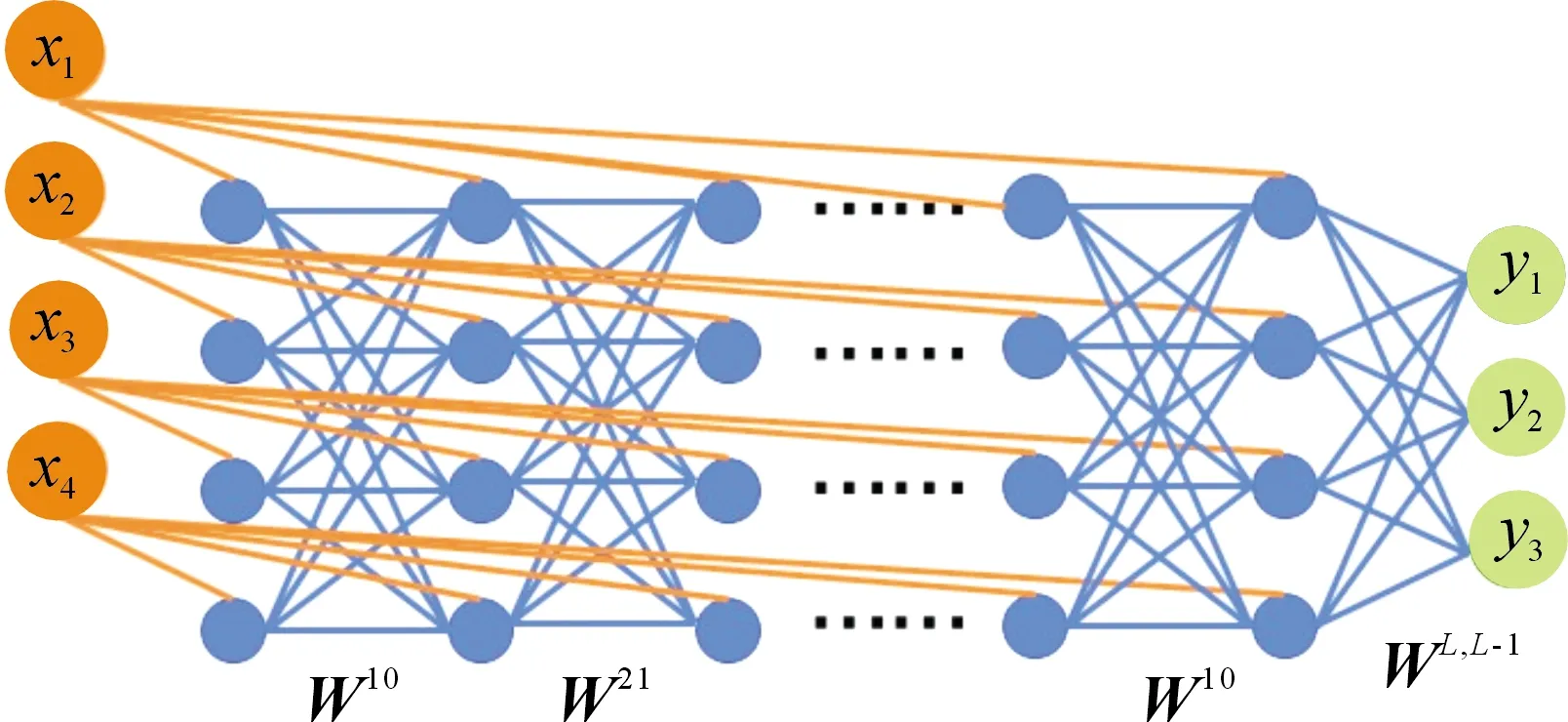
图2 一个4输入和3输出的树突网络

2) 树突网络学习规则

树突网络使用均方误差的一半作为损失函数。树突模型描述了一种基于错误反向传播的DD学习规则，该学习方法的简单性使树突网络可以方便地用于不同领域。以下等式描述了其学习规则。

树突模型的正向传播：

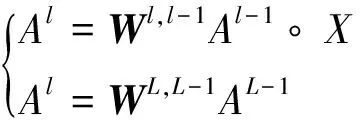
(14)

树突模型的反向传播：

(15)

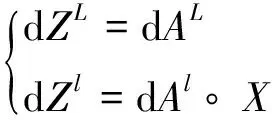
(16)

dAl-1=(Wl,l-1)TdZl

(17)

树突模型权重的迭代：

(18)

Wl,l-1(new)=Wl,l-1(old)-αdWl,l-1

(19)

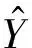
3) 响应值与变量参数的函数关系

本文构建一个3输入2输出、DD模块为2的树突模型，迭代次数设置为100 000，学习率为0.01。通过树突网络回归后，可以得到响应值Y1和Y2与变量参数的函数关系，具体见式(20)(21)。

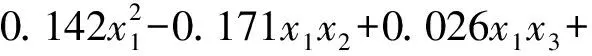
(20)

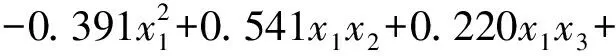
(21)

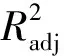
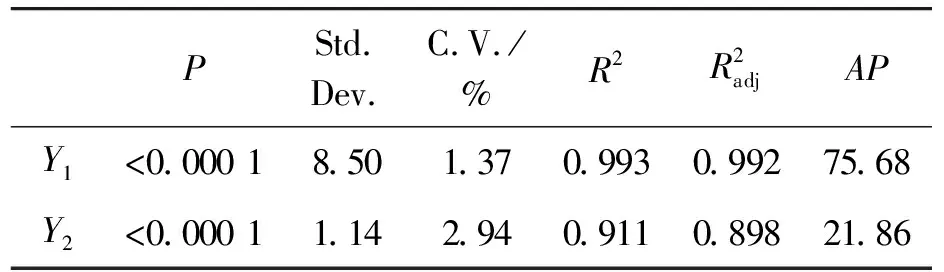
表5 Y1和Y2回归模型误差统计评估

综上所述，响应值Y1和Y2的拟合函数能够检验参数且能够替代真实模型，将其构成多目标优化函数D，见式(22)。

(22)

2.4 NSGAⅢ的多目标求解

本文针对多目标优化函数D运用非支配排序遗传算法NSGAⅢ进行求解。Deb等[13]在NSGAⅡ算法通过拥挤度来选择子代个体，NSGAⅢ在NSGAⅡ的基础上采用参考点选择机制挑选子代个体，使其更容易找到全局最优解。Guillermo等[14]证明了在小规模样本中，NSGAⅢ性能略好于NSGAⅡ；大规模样本、目标函数大于2时，其性能远超过NSGAⅡ。因此，为获取优良的多目标解，选择NSGAⅢ进行求解。

NSGAⅢ的重点是如何通过参考点进行子代个体的选择，首先根据下列公式生成参考点个数：

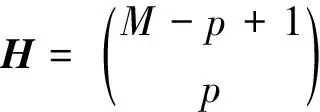
(23)

式中：H为参考点个数；M为多目标函数个数，为目标函数在超平面轴上的分段数。

接着是计算极值点，针对M个目标函数，极值点公式如下：

(24)

(25)

式中：wi=10-6；fi(x)为种群个体的目标值；zi,min为种群个体在每个目标函数上的最小值，通过ASF可以求解出超平面与坐标轴的截距ai。

最后，种群目标值归一化，可表示为：

(26)

通过式(26)可将参考点映射到超平面上，基于小生镜保留操作进行个体选择，直到满足种群规模。参考点如图3所示，算法流程如图4。

NSGAⅢ算法设置如下，初始参考点为20，初始种群数量为100，交叉率50%，变异率2%，迭代500次。算法在Win10平台Matlab R2016a中运行。

选取部分帕累托解与初始结构进行比较，得到表6，其中优化结构的出口温度最多降低了67.39 K，蓄热效率最高提高了2.49%。优化结果表明：通过响应面方法对蓄热室的结构参数进行优化，可以有效提高蓄热效率，同时降低加热期出口温度。

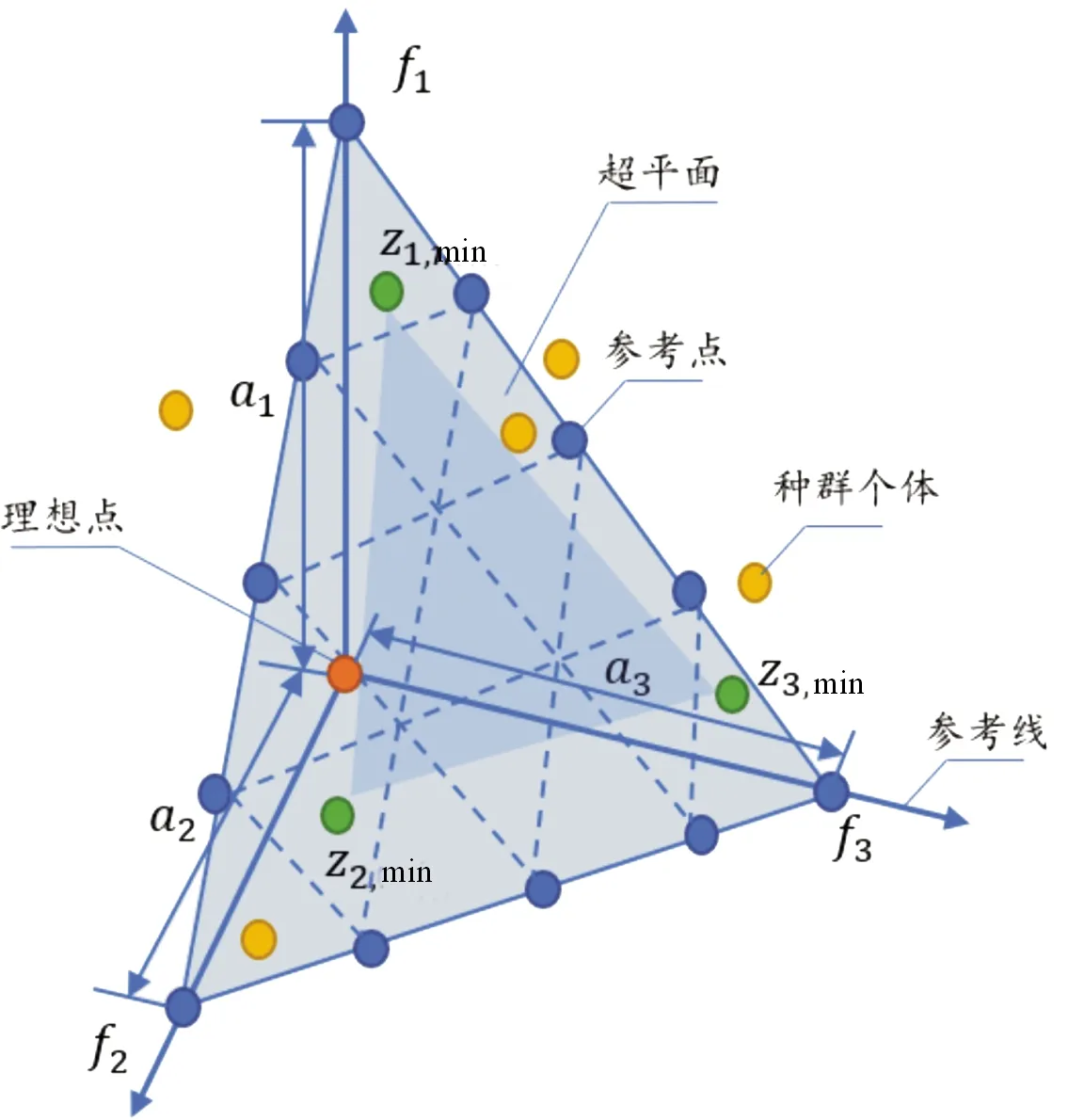
图3 参考点示意图

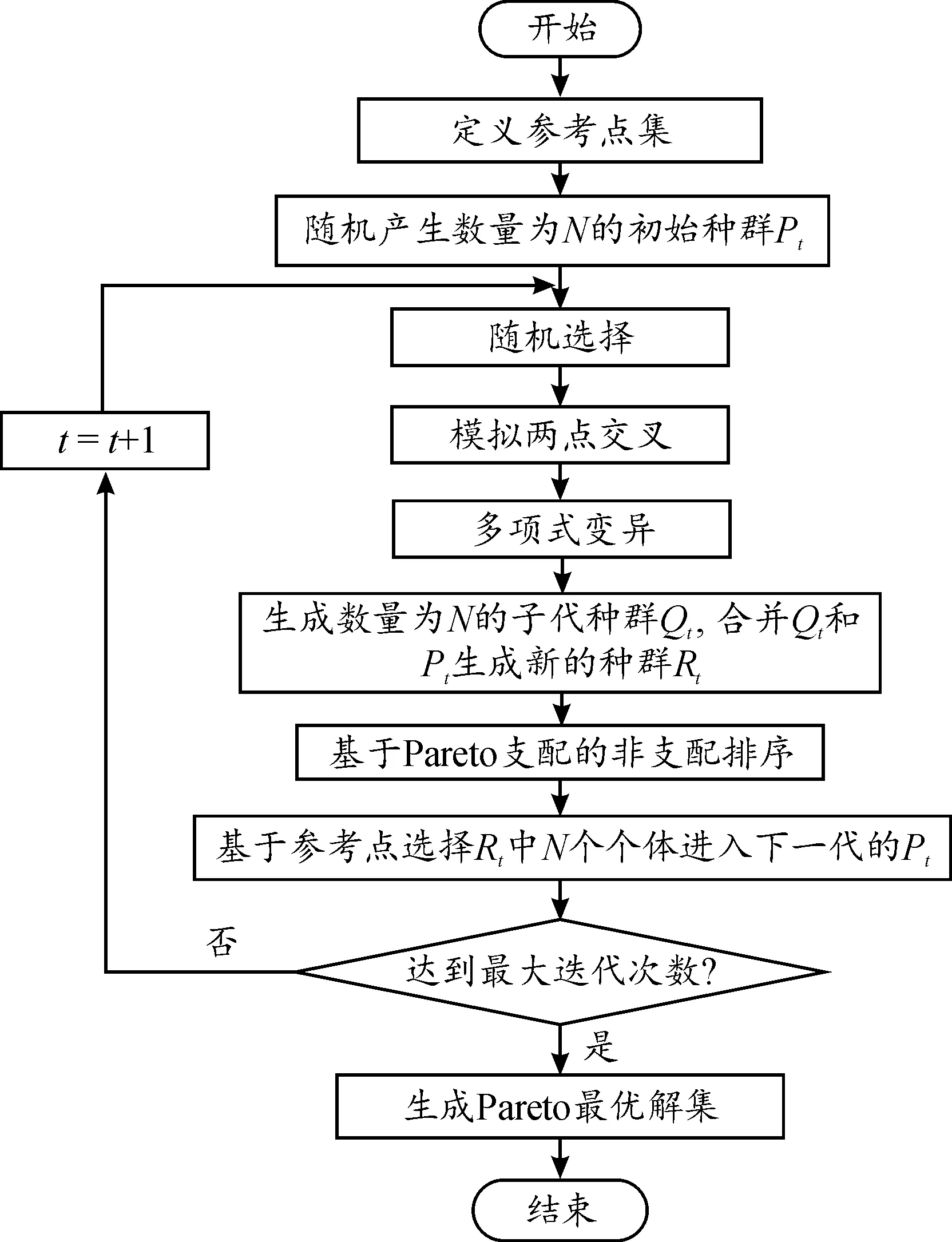
图4 NSGAⅢ算法流程框图

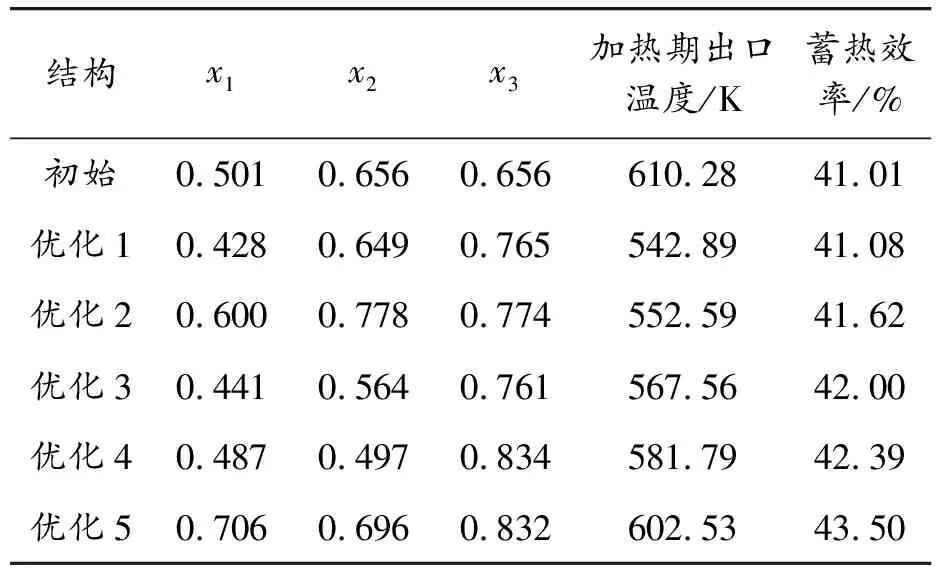
表6 初始结构与部分最优帕累托解集

将优化结构5进行模拟仿真，仿真后的加热期出口温度和蓄热效率为597.72 K和43.71%，与帕累托解相差7.98%、4.83%，证明了帕累托最优解的可靠性。图5显示了蓄热室中心位置的高温烟气温度沿蓄热室高度的变化，优化后的高温烟气在蓄热室中心处温度更低，说明蓄热室吸收了更多高温烟气的热量。图6显示了蓄热室优化前后出口温度随时间的变化，优化后的蓄热室出口温度更低，同样证明了蓄热室吸收了更多高温烟气的热量。

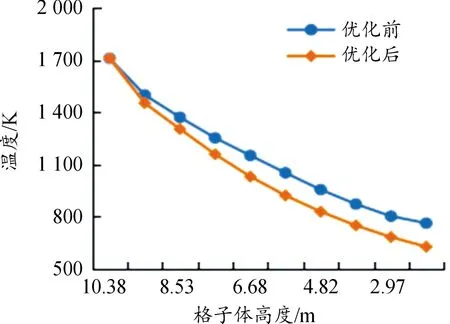
图5 蓄热室中心处优化前后温度随高度变化的曲线

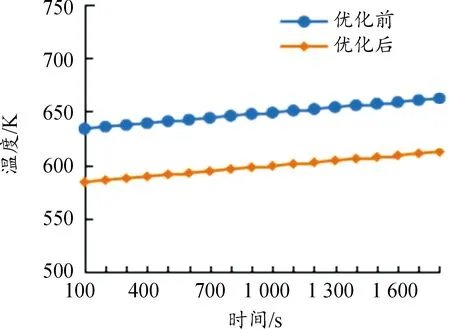
图6 蓄热室优化前后，出口温度随时间变化的曲线

图7显示了优化后的蓄热室高温烟气温度分布比优化前更均匀，优化后的高温烟气集中分布在蓄热室后部。

3 树突网络与BP神经网络比较

树突网络与传统机器学习算法比较其特点在于拥有良好的泛化能力及更好的精度。将树突网络与BP神经网络进行对比，首先将表4中的数据进行归一化处理，归一化公式为：

(27)

采用相同的训练集、验证集(都采用3层结构体)，构成一个3输入2输出的网络结构，训练 100 000次，学习率均为0.01。树突网络的MSE远小于BP神经网络，通过训练得到的结果如图8、9所示，可以看到树突网络能够更好地拟合实验结果，而BP神经网络稍差一些。树突网络的另一个优势在于其白箱性质，可以通过增加胞体结构数量提高精度。保持其他设置不变，只将树突与BP神经网络的3层结构体逐步提高到5、7层，通过表7可以看到树突网络的MSE是随着胞体结构的增加而逐步降低的，而BP神经网络并没有出现随着胞体结构增加而MSE降低。因此，树突神经网络能够更好地进行回归并得到精确的响应值。

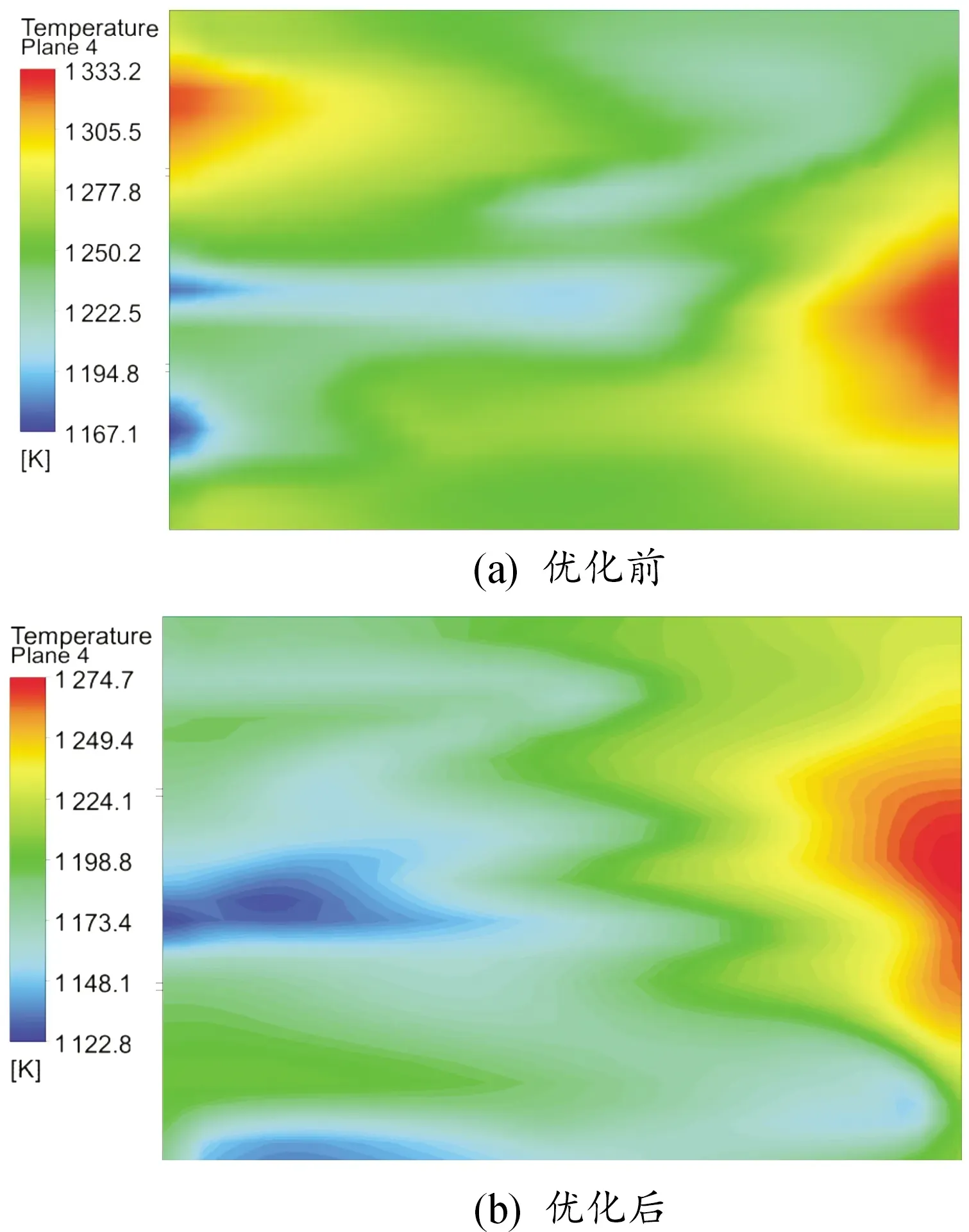
图7 蓄热室横截面优化前后的温度云图

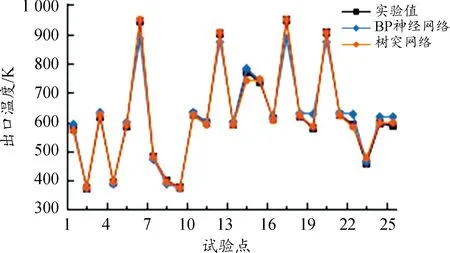
图8 BP神经网络与树突网络预测出口温度曲线

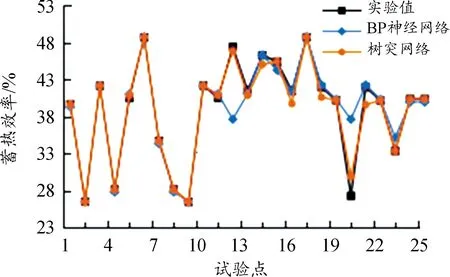
图9 BP神经网络与树突网络预测蓄热效率曲线

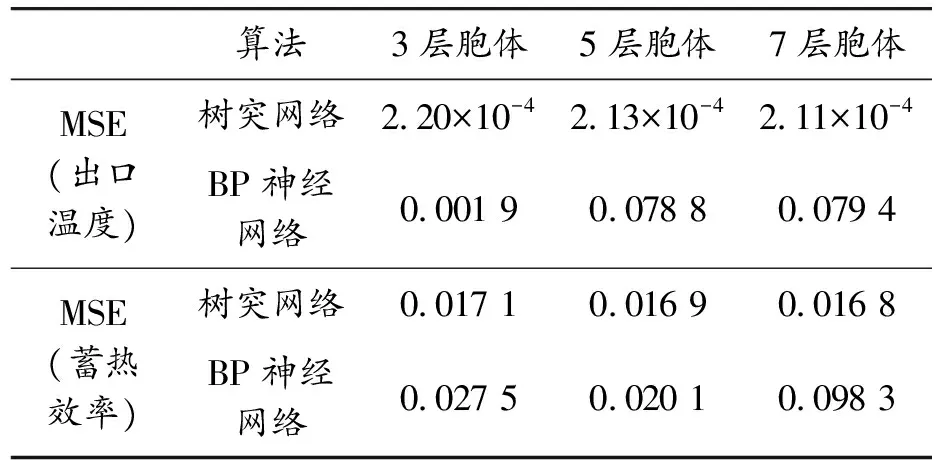
表7 树突网络与BP神经网络的MSE

4 结论

1) 多孔数值模型能够较好地模拟蓄热室的实际工况，模拟得到的加热期蓄热室各高度部位的温度与实际测量温度误差不超过4.2%。

2) 树突网络得到的加热期出口温度和蓄热效率回归函数能够较好地模拟实际情况，Y1和Y2决定系R2为0.993和0.911。通过NSGAIII算法可对其进行有效优化，优化后的结构与初始结构相比，出口温度可降低28.49 K，蓄热效率可提高2.3%。优化结构5的模拟仿真结果与帕累托解相差7.98%、4.83%，证明了帕累托解的可靠性。

3) 本研究展示了树突网络的优点，在相同条件，树突网络比BP神经网络拟合精度更高，通过提高胞体数量可以提高拟合精度。