基于改进组合赋权-逼近理想解排序法的综合能源系统规划方案综合评价

陈 曦，彭泓华，曹 杰，袁梦玲，穆静霞，王 悠

(1.重庆理工大学 电气与电子工程学院， 重庆 400054;2.重庆工程职业技术学院 大数据与物联网学院， 重庆 402260)

随着我国成为世界上最大的能源生产国和消费国，传统的能源生产和消费形态不再适应未来的能源需求挑战。可再生能源和储能等新技术的不断成熟、装机规模的持续增长为建立新型能源电力系统提供了技术和经济方面的可行性。因地制宜，建立适合不同场景需求的综合能源系统(integrated energy system，IES)是助力能源革命的重要抓手[1]。目前，国内外针对综合能源系统的研究主要集中在规划设计[2]、运行调度[3-4]和模拟仿真[5]等方面，建立面向综合能源系统的科学评价体系对于选取合理有效的IES规划方案和项目决策评价具有重要意义。评价指标的选取和合理赋值是进行综合能源系统综合评价的前提。主流方法按赋值方式分为主观赋权法、客观赋权法和主客观赋权法，其中主观赋权法多适用于难以量化的定性指标，有德尔菲法、层次分析法等[6]；客观赋权法多用于需要消除受主观判断影响的定量指标的条件，有变异系数法和熵权法等，主要应用集中在输电线路可靠性、可再生能源利用率以及居民供能方案合理性等简单维度的评价方面[7-14]。由于综合能源系统的评价受政策、经济、安全、环保等复杂多维度因素的影响，简单维度的评价模型并不适用[15-16]。近年来，有学者提出运用层次分析法(analytic hierarchy process,AHP)与熵权法(entropy weight method,EWM)结合，构建多准则的评价指标体系来综合分析技术、经济、环境、社会等因素的影响[17-18]。组合赋权是一种根据对象特点采用不同方法进行赋权加和，最终得到能同时保留主观判断因素和体现数据统计性的综合权重的主客观赋权法。层次分析法可以通过对多因素的比较分析量化决策者经验，适用于结构复杂且数据缺乏的情况。熵权法可以根据指标信息熵的效用价值确定权重。但传统的熵权法因灵敏度高易造成指标失效[19]，因此本文中对传统熵权法进行改进，在确定客观权重时考虑修正系数，构建以AHP-改进EWM相结合的改进组合赋权法，用于综合能源系统评价指标的赋值。

在确定各指标的综合权重后，选取合适的综合评价方法。若不考虑评价指标与评价值的函数关系，仅进行简单的线性求和，则难以保证决策结果的合理性。逼近理想解排序(technique for order preference by similarity to ideal solution，TOPSIS)能够充分利用原始数据的信息，客观真实地反映方案间的差距，既能避免主观因素的干扰，也考虑了客观评价未考虑到的经验问题，因此在卫生决策[20]、城乡生态文明建设[21]等领域多有应用，近年来也被用于电力系统风险评估[22]、综合能源系统效益评价[16]等方面。

基于上述研究，针对综合能源系统评价这一多维复杂的决策问题，首先，从规划方案的技术性、经济性、可靠性及环保性4个层次提出具有普遍适应性的16维评价指标体系；然后，采用层次分析法和改进熵权法相结合来改进组合赋权法确定各指标的所占权重，进而利用TOPSIS计算优劣解距离来确定规划方案的评分函数；最后，结合实际案例进行评价分析。

1 综合能源系统规划方案评价指标体系

1.1 综合能源系统结构

综合能源系统是能源互联网的载体，是集电力网、天然气网和冷/热网的多耦合、多时空尺度的源-网-荷一体化系统，综合能源系统结构示意图见图1。在规划综合能源系统时，通常设置有变电站和配电网络。考虑资源利用的最大化和环境效益的最大化，为降低碳排放成本，将风电机组、光伏机组、燃气轮机等作为能源输入，利用电锅炉、电制冷机、燃气锅炉、吸收式制冷机等能量耦合设备实现能量的梯级利用。

图1 综合能源系统结构示意图

1.2 建立评价指标体系

根据综合能源系统的评价指标体系构建原则和德尔菲法[23]，通过向能源业相关学者反复咨询，在保证评价指标的全面性、合理性和科学性的前提下，确定如图2所示的评价指标体系结构。

图2 评价指标体系结构框图

评价指标体系主要通过准则层及指标层等来体现。准则层包含技术性指标、可靠性指标、经济性指标和环保性指标等四层指标体系。指标层主要由16个二级指标来体现。技术性指标是决定规划方案是否能够成功落地的关键；可靠性指标是对规划方案的供能能力及运行能力进行评估；经济性指标是直接反映工程项目经济效益的重要指标，常常是投资者、决策者首要考虑的内容；环境性指标能够反映综合能源系统规划方案的环保与清洁程度，是顺应未来绿色、低碳、环保需求的社会主流意识[24]。本文中构建的指标体系旨在针对各种综合能源系统的不同规划方案进行科学合理的评价，得到能满足决策者不同需求的规划建设方案。

1.2.1技术性指标

1) 清洁能源占比。通过计算清洁能源在整个系统年用电量的贡献程度来表示清洁能源在该能源系统中的利用情况。

(1)

式中：θ为清洁能源占比；Ek表示第k种清洁能源为目标系统提供的能量；Ei为目标系统消耗的第i种能量。

2) 能源利用率。能量利用水平的高低是衡量能源利用效率的重要指标之一，也代表能源被有效利用的程度，反映了能源系统总体运行水平的高低。

(2)

式中：P0为系统运行时的净输出电量；QH为系统运行时的输出热量；QC为系统运行时的输出冷量；W为系统运行过程中的天然气消耗量；LHV为天然气低热值；P为输入系统的电量。

3) 系统可维护性。指系统发生故障后，经过维修后能恢复正常工作的程度。

4) 系统运行稳定性。对于综合能源系统而言，系统运行过程中能满足负荷高峰时段安全平稳运行需求；负荷骤变或外界极端天气等不利条件下，技术参数能保持在合理数值范围内，不出现设备损坏等大的安全事故，能较好满足用户负荷需求，保证良好的换热效果。

1.2.2可靠性指标

方案的可靠性评价主要是指对方案的供能能力及运行能力进行评估。

1) 最大负荷转供能力。系统中某能源子网出现供能不足或故障时，其他能源子网通过能源转换设备为其供能，满足整个系统正常运行的能力。

PLE=POE-POS

(3)

式中：PLE、POE、POS分别为最大负荷转供能力、当前功率输出总和、能源转换设备的输出功率总和。

2) 系统能源供应不足率。计算模型为

(4)

式中：PE为系统中的电负荷需求量；HH为系统中的热负荷需求量；QC为系统中冷负荷需求量；ΔPE、ΔHH、ΔQC分别为系统中电能、热能、冷能的供应缺额，计算式如下：

(5)

式中：Eres、EMT、QHC、QEC、HWH、HEH分别为新能源出力、燃气轮机发电量、吸收式制冷机输出冷量、电制冷机输出冷量、余热锅炉输出热量和电锅炉输出热量。

3) 供能可靠率。反映系统为用户或设备供能能力的指标，一般以用户在一年中获得的供能时间与系统的总供能时间的比值来表示。

(6)

式中：Nl,i为供能网络的用户数；Ul,i为负荷点平均停用时间。

4) 最大供能能力。当系统处于最大供能模式运行时，一旦负荷出现细小的变化，系统的稳定性将被破坏，可能造成系统故障。系统处于这一临界的状态被定义为系统的最大供能能力[25]。

(7)

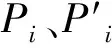
1.2.3经济性指标

综合能源系统规划方案的经济性评价是直接反映工程项目经济效益的重要指标，决定了项目实施的可行性。

1) 规划投资成本

(8)

式中：i、Si、ωi、Yi分别为设备i的类型、额定容量、单位投资成本、使用寿命；r为折现率，本文中取值为0.04。

2) 系统运行成本。主要为购电成本和购气成本，其模型为：

(9)

式中：Hi,t为设备i在t时刻的燃气消耗量；VLHV为天然气燃烧热值，本文中取值为10.8(kW·h)/m3；m、p、Et分别为电价、天然气价格、t时刻系统向电网的购电量。

3) 系统维护成本。由系统初次投资成本决定，本文中系统维护成本按照初次投资成本的3%计算[26]。

Ct=3%Cn

(10)

4) 投资回收期

(11)

式中：fre为综合能源系统输出与原天然气储气库系统相同的冷、热、电量所需的增量投资；ftr和fint分别为原系统和综合能源系统的年运行费用，包括燃料成本、人工成本、设备维护成本和设备折旧成本等。

5) 系统运行寿命。系统中包含的全部设备自全新状态开始使用，直到核心设备无法稳定运行，不再具有正常功能而停止使用的全部时间。

1.2.4环保性指标

为总体反映综合能源系统规划方案的环保与清洁情况，将年CO2、年SO2和年NOx减排率作为本文的环保性重要评价指标。污染物年减排率为：

(12)

1) CO2排放量。碳排放主要来自于燃气轮机、燃气锅炉及电网等3部分。为形象地表示碳排放量，引入碳排放因子分别表示用电的碳排放及用气的碳排放。其模型表示为：

(13)

2) SO2、NOx等排放量

MX=FβX

(14)

式中：MX为污染物X的产生量；F为系统燃料总量；βX为燃气X污染物的排放系数，其中X为SO2时取值0.011，为NOx时取值0.202。

2 评价方法

对综合能源系统规划方案的评价属于涉及多因素的复杂问题，很难采用单一的评价指标对规划方案进行评价，为此，本文中采用AHP-改进EWM相结合的方法来确定各方案指标权重，并采用TOPSIS进行方案评价。

2.1 主观权重确定—层次分析法

AHP通过定性指标和模糊量化方法实现从定性到定量的转化，以此解决多目标、多方案优化决策问题[27]。其基本步骤如下：

步骤1层次架构模型的构建。将不同决策目标问题进行系统化、层次化，形成多维度的评价体系，如图3所示。

图3 方案评价体系流程框图

步骤2判断矩阵的构建。根据构建的层次构架模型，在实际判断中常采用1～9标度法对各指标的相对重要性进行判断，并构造决策模型的判断矩阵Ax=(aij)m×n，其中aij表示bi相对于bj的相对权重。

步骤3判断矩阵一致性的检验。由于判断矩阵偏向于主观性和随机性，易出现严重的不一致现象，为此需要对判断矩阵进行一致性检验[23]，根据一致性检验的公式[28]：

(15)

通常认为CR≤0.1时，判断矩阵满足一致性检验；否则，需要调整判断矩阵，使其满足一致性检验。

步骤4层次权重的确定。判断矩阵通过一致性检验后，求取其最大特征向量，即为各指标的主观权重φj。

2.2 客观权重确定—改进熵权法

熵权法根据指标变异性的程度来反映指标信息熵值的效用价值。其基本思想是：若某项指标熵值较小，则说明该指标的信息熵提供的信息越多，其客观权重也应越大[29]。评价过程中仅通过熵的定义进行计算时存在一定误差，即当信息熵值越靠近1时，信息熵值很小的波动就会使熵权的结果发生成倍数的变化，造成计算结果不合理。为此，本文中利用改进后的熵权法[30]对指标进行客观赋权。具体如下：

1) 建立评价矩阵X。根据拟定的方案数据，建立原始信息矩阵为X=xm×n，m为待评估的规划方案，n为准则层的评估指标。

(16)

2) 指标归一化处理，得到标准化矩阵Pij。

(17)

式中：1≤i≤m； 1≤j≤n。

3) 计算指标信息熵ej。

(18)

(19)

其中，当yij=0时，yijlnyij=0。

4) 权值计算。由于熵权法本身存在求取熵权不足的问题，故引入修正权重系数法对熵权法进行改进：

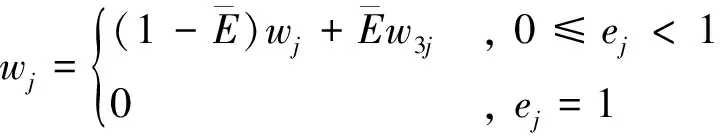
(20)

(21)

(22)

2.3 综合权重计算

为降低层次分析法及熵权法的主客观权重对评价指标的影响，不同于文献[10]，本文中熵权法引入修正权重系数法弥补熵权求取不足的问题，并采用最小二乘法对主客观权重值进行优化[28]，进而得到各评价指标的综合权重。最小二乘法优化综合权重模型为：

[(φj-μj)sij]2}

(23)

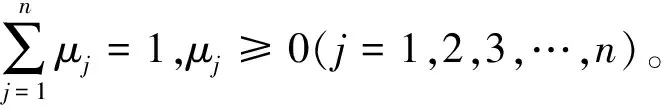
采用拉格朗日乘数法求解上述模型，得到综合权重值βj为：

(24)

综合权重向量为β=[β1,β2，…,βj]T。

2.4 基于TOPSIS的方案评价

TOPSIS法是多目标决策分析中对多对象的系统性评价和分析的方法[31]。通过加权欧式距离计算、正理想解和负理想解的贴近程度，对评判对象进行排序，根据相对贴近度来评价方案的优劣性。

1) 标准化决策矩阵

(25)

式中：i=1,2,…,m；j=1,2,…,n；rij为归一化第i个选择方案的属性值j。

2) 计算加权标准化决策矩阵

vij=βj×rij

(26)

式中：βj是属性值j的权重。

3) 确定正理想解和负理想解

(27)

式中：A+表示正理想解,A-表示负理想解。

若属性j表示利益属性，则：

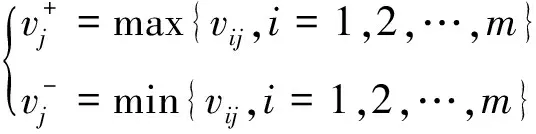
(28)

若属性j表示成本属性，则：

(29)

4) 计算每个备选方案到A+和A-的距离

(30)

(31)

5) 计算最接近理想解的方案

(32)

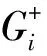
6) 方案排序，按照Ci依次递减的顺序排列。

3 案例分析

以文献[32]中提出的综合能源系统规划项目为例，采用本文方法开展评价分析。综合能源系统能源服务区主要包括天然气储气库、储气库周边与储气库用能特性相匹配的工商业企业。根据储气库的能源结构和可利用资源分析，以规划期内总投资运行成本最低进行优化配置，各规划方案配置结果见表1。

表1 各规划方案配置结果 MW

对以上4个规划方案应用第1.2节构建的综合能源系统规划方案的评价指标系，分别对各项指标进行测算，形成对各方案的指标评价。根据各规划方案配置结果计算出的16项定量指标参数见表2。

表2 各方案指标参数计算

续表(表2)

3.1 评价指标权重计算

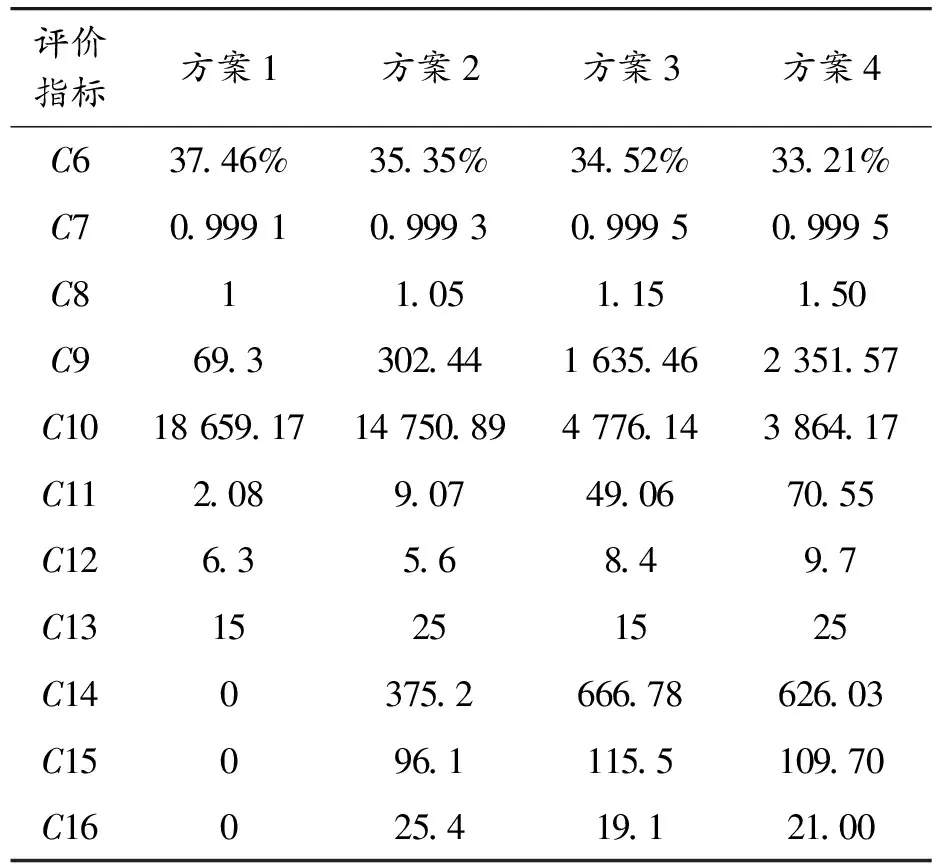
1) 层次分析法计算主观权重。以实际对业务造成的影响力，根据专家经验和决策者意见，得出重要性排序：可靠性>技术性>经济性>环保性。对准则层和指标层分别进行主观赋权，得到准则层主观权重w′和方案层指标对应的主观权重w″。

步骤1 计算准则层指标主观权重。判断矩阵为：

检验判断矩阵的一致性：

判断矩阵满足一致性要求，指标权重为：

步骤2 计算各指标层主观权重。判断矩阵为：

经一致性检验，得到各指标权重如下：

综上，得到准则层指标重要性为：可靠性>技术性>经济性>环保性。采用加权计算得到方案层的各指标主观权重，见图4。

2) 改进熵权法计算客观权重。根据前述步骤对原始数据进行量纲为一化及归一化计算，得到各准则层指标熵权wj=[0.221 3 0.301 9 0.346 0 0.130 9]，即改进熵权法认为准则层指标重要性为经济性>可靠性>技术性>环保性。最终计算得到16项指标的客观权重，见图4。

3) 计算综合权重。利用最小二乘法对方案层各指标的主客观权重进行组合，优化求解得到综合权重，利用单一熵权法计算的权重结果见图4。

图4 各项指标权重示意图

采用拉格朗日乘数法求解得到综合权重βj=[0.272 3 0.412 7 0.221 0 0.094 2]，即经过最小二乘法组合优化后认为，各准则层指标重要性排序为可靠性>技术性>经济性>环保性。

3.2 规划方案的评价结果

由2.4节式(25)—(32)计算得到整体的方案贴近度为：

其中G取值范围为0～1，G越大，表明越贴近最优解，系统评价越好。

考虑到百分制评分更便于决策者进行方案对比评估，故由TOPSIS法引入得分函数SCORE[33]，即：

(33)

用SCOREi替代Gi作为候选方案的评分，使方案评分值基本落在0～100区间内，有利于决策者根据各方案得分情况做出直观决策。

由图5可知，方案4得分最高，能使资源利用最大化。结合图6分析发现，方案4中包含多个优项指标，其中C1、C2、C3、C5、C8、C9、C11、C12的权重占比均优于其他方案，故评分为最高；方案3也有多个优项指标，其中C4、C14、C15指标权重较小，故综合评分仅次于方案4；方案2中C4、C6、C8、C10权重较优，其余指标权重占比小，故评分排第3；方案1中有多个指标与其他方案同指标相比相差较大，故评分最低。

图5 方案得分情况直方图

图6 指标加权标准化结果直方图

综上，在进行以规划期内总投资运行成本最低为目标的天然气储气库综合能源系统规划研究时，考虑多种能源形式的规划方案最优。

由于本文中各指标的差异性过小，传统熵权法存在的灵敏度过高的情况不明显。由于熵值的大小对客观权重的影响很大，从图4中可以看出，指标C8、C13与改进熵权法求得的客观权重差异较大，主要原因就是因为传统的熵权法有时会存在灵敏度过高造成指标失效的情况。

3种方法的评价结果一致，相较于传统熵权法和文献[15]中的反熵权法，采用本文的改进熵权法后求得的贴近度更高，能更加真实地反映各方案的综合得分情况。4种方案的方案贴近度见表3。

表3 方案贴近度

4 结论

以某综合能源系统为例，分别从技术性、经济性、可靠性及环保性等4个角度建立3层16项指标的方案评价体系，通过层次分析法和引入修正权重系数的改进熵权法得到评价指标的主客观权重；将定性问题定量化，克服了熵权法灵敏度过高的缺点，采用最小二乘法对主客观权重进行优化，使得到的各指标综合权重更为科学合理；将综合权重融入TOPSIS，采用加权欧式距离度量正理想解与负理想解的距离，以此获得各方案的相对贴近度；通过相对贴近度排序实现各规划方案的有效综合评价，使评价结果更加清晰化。评价结果能实现对规划方案的综合科学评价，与其他主流方法评价结果一致，但对于不同规划方案，其在不同准则层和评价指标的刻画方面更为直观和准确。新评价方法可为规划投资者和决策机构在综合能源系统前期规划方案决策和评价时提供参考。