碳达峰目标下我国煤炭消费量预测与分析

贾大任，王建民

(安徽理工大学 经济与管理学院，安徽 淮南 232001)

煤炭资源在我国能源结构中占据着重要位置，虽然近年来煤炭资源在能源结构中的占比有所下降，但是依旧达到了57%左右(2020年)。随着我国经济从依靠资源消耗发展模式转变为高质量发展模式，追求更少的资源消耗成为当今社会研究的课题。习近平总书记在第七十五届联合国大会一般性辩论中指出，我国力争二氧化碳的排放在2030年前达到峰值，在2060年前实现碳中和，即实现碳达峰的目标和碳中和的愿景[1]。

在我国当前能源结构下，实现经济增长需要一定的能源消费。煤炭能源的消费是碳排放的主要来源，增加煤炭能源消费势必会造成碳排放的增长，这给我们同时追求经济发展和碳减排的双赢目标带来挑战。

实现碳达峰的目标和碳中和是我们的美好愿景，要实现这个愿景，减少能源的消耗尤其是煤炭能源的消耗是基础和关键。但是，这并不意味着绝对不使用煤炭资源，在碳达峰战略背景下如何控制煤炭消费量，实现碳达峰目标和经济增长的双赢发展是我们必须要面对的重要问题。

一、文献综述

国内许多学者都针对煤炭消费量的研究，如门东坡、王金力[2]等采用最优加权组合模型对煤炭消费结构进行预测，得出了我国未来煤炭消费总量会有小幅度增长的结论；王亚珍[3]等以煤炭消费的供给侧和需求侧两方面为基础构建模型，采用VAR模型以及Granger因果检验的方法，研究结果表明经济发展和人均煤炭消费量之间存在着单向的Granger的因果关系；刘威[4]等人基于回归分析、时间序列分析的方法，建立了多元回归模型和时间序列模型以及神经网络模型，对影响秦皇岛市动力煤价格的主要因素及其影响程度进行了分析，并依据分析的结果对秦皇岛市动力煤的价格进行了预测；李润宸[5]利用了LSTM模型构造了煤炭消费量模型，对煤炭消费的时间序列变化规律进行了预测，以此来为参与者提供煤炭消费市场的借鉴；赵宇[6]利用多元回归模型和灰色预测模型对江苏省农业碳排放的动态变化进行了影响因素分析和趋势预测，结果表明江苏省的农业碳排放量呈先下降、再升高、再下降的趋势，并预测了在2016—2030年间会呈现下降趋势；冷建飞[7]等人利用多元回归的分析方法，以民航客运量的实例证明了多元线性回归方程回归结果具有科学性；陈喆[8]采用VECM模型研究了煤炭消费与低碳经济发展二者的因果关系，发现了低碳经济的发展对煤炭消费的影响程度较为明显。

综上所述，许多学者使用多元线性回归法对其研究主体的影响因素进行分析、对煤炭消费量进行预测。但是在现有研究中，使用多元线性回归法对煤炭消费量进行研究的文献不多。针对这种情况，以现有的文献与研究为基础，更进一步展开了研究分析：①在实现碳达峰目标背景下，采用多元线性回归的分析方法，探讨影响煤炭消费量的因素；②根据煤炭消费量的趋势、影响因素，构造了我国煤炭消费量多元线性回归预测模型，对实现碳达峰目标下的煤炭消费量进行动态全景式预测；③以2004—2017年的相关数据的分析作为预测基准，预测的结果将为煤炭消费控制战略提供数据支持，并且能够发现碳达峰目标对煤炭消费量、产业结构调整以及包括能源利用效率和产业技术进步在内的技术创新的影响，也能够进一步化解经济高质量发展和减少能源资源消费如何双赢的困局。

基于此，以煤炭的消费量入手，综合考虑现实状况，分析影响煤炭消费量的主要因素。根据分析所得结论，总结进行煤炭消费量预测的启示，目的是为能源消费调整、实现碳达峰的目标和碳中和的愿景打下坚实基础。

二、研究设计

1.构建多元线性回归模型

多元回归分析将一组相关变量中的其中一个作为因变量，其他一个或多个变量作为自变量，从而建立起多个变量之间的线性、非线性数量关系模型，并使用样本数据进行分析的统计分析方法。多元线性回归模型在包括收入差距[9]、并网光伏发电[10]、环境领域[11]及地区用水需求量[12]等诸多领域进行过重要的分析预测，并以实践证明了该模型具有科学性和实用性。

在针对实际问题的分析解决中，我们可以发现，通常影响一个变量Y的因素由许多个预测变量X构成。若由n个预测变量构成，则这些预测变量可以表示为Xn(n=1,2,3,…,n)，预测变量Xn与变量Y之间存在相关关系，即当预测变量Xn有一个定值时，那么变量Y便会有一个相应的值与之对应。所以，多元线性回归模型可以表示为式(1)。

Y=C+β1X1+β2X2+β3X3+…+βnXn+α

(1)

在式(1)中，C表示常数项，α表示随机误差，β1、β2、β3…βn即回归系数。在该多元线性回归模型中，为了保证能够达到所期望的预期效果，必须要使得所选择的预测变量X对变量Y有明显的相关性和显著的影响，并且所选择的预测变量之间也要呈现互斥性。经过对模型运行分析得到多元线性回归方程后，要经过检验和修正的步骤，以此来保证其准确度和可信度。

2.数据来源

所用数据均摘取自国家统计局网站发布的年度数据，分别由指标栏目中的子栏目国民经济核算、人口等选取相关数据。由于煤炭消费量暂只公布至2018年，所以选取数据年份为2004—2017年，多元线性回归方程建立后，以2018年发布的相关数据为准进行模型的检验和修正[13]。

在选取的数据中，根据已建立模型的需要，将煤炭消费总量作为变量Y，其影响因素作为预测变量。其中，将国内生产总值记为X1、工业生产总值记为X2、全社会固定资产投资记为X3、城镇人口数量记为X4、社会消费品零售总额记为X5，由此展开处理与分析。

三、数据处理与分析

1.数据处理

将原始数据上传至SPSS软件，选择分析-回归-线性，将煤炭消费量(Y)作为因变量，将国内生产总值等(X1,X2,…,Xn)记为自变量。根据研究分析需要，特做出以下选择。

(1)因为要研究煤炭消费总量的影响因素，所以根据回归方程性质，选择步进的方法，软件系统能够根据事先设定好的F统计量的概率值进行自动筛选和过滤，最先进入回归方程的自变量是与因变量相关性最大、贡献最多的，根据进入顺序依次递减。

(2)在分析检验中需要选择估算值、模型拟合、共线性诊断和个案诊断。在离群值中以默认的3倍标准差为准，此为异常值依据，也就是说当残差超过3倍标准差的观测时会被看做异常值处理。而之所以要选择共线性诊断，是因为本模型中的预测变量有5个，若其中有2个或2个以上的预测变量之间存在线性相关关系，即会产生出多重共线性现象。

(3)在系统作图中，我们通常以自变量作为X轴，用残差作为Y轴。但是为了照顾完整的情况、不忽略特殊，所以以标准化预测值ZPRED作为X轴，分别用血生化剔除残差SDRESID；以标准化残差ZRESID作为Y轴，分别作为两组绘图变量，并且选择作出直方图，以便对导出的结果进行直观分析。

(4)选择库克距离、平均值、单值和标准化。之所以选择库克距离，是为了以库克距离的大小来判断个案对回归系数的影响。

2.运行结果及分析

在对上传的数据和根据研究需要作出选择后，运行SPSS软件，会首先得到在构建模型时选取的5个预测变量中被输入和被除去的变量，结果如表1所示。

表1 输入/除去的变量a

如前所述，由于采用的是步进法，所以先进入模型的相关性最强且贡献最大，后者次之。由表1可知，由先进入模型的城镇人口数量建立的模型1，由后进入模型的社会消费品零售总额建立的模型2。根据相关性强弱和贡献性大小我们可以知道，影响煤炭消费总量最关键的因素是城镇人口数量，其次是社会消费品零售总额。

根据对煤炭消费总量影响程度的大小，进一步得到关于由城镇人口数量和社会消费品零售总额构建的两个模型的摘要，如表2所示。

表2 模型摘要c

从表2可以得知，在构建的两个模型中，观察R2即可知拟合优度。显然，由社会消费品零售总额构建的模型2的R2为0.908，优于由城镇人口数量构建的模型1。

在比较所构建的两个模型的拟合优度后，进一步得到ANOVA表，以此来判断因变量和自变量之间是否存在线性关系。ANOVA表如表3所示。

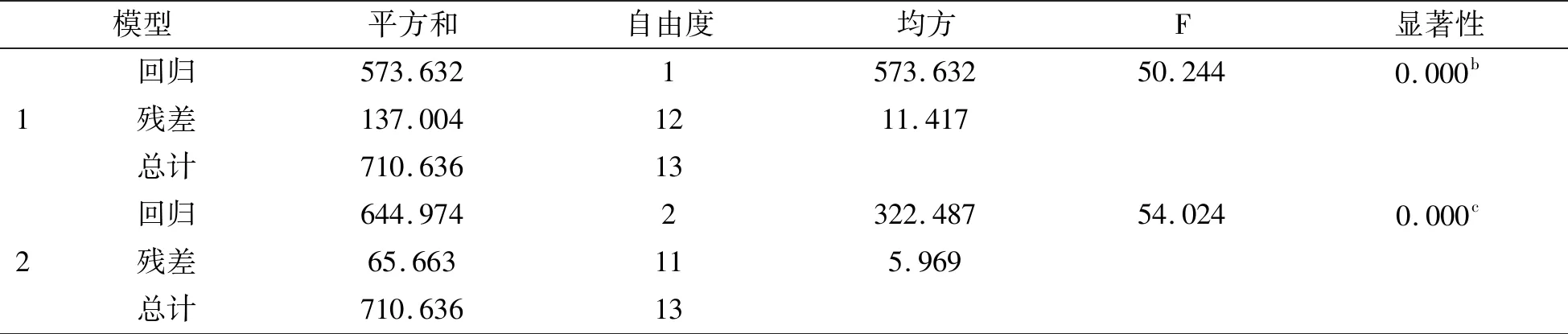
表3 ANOVAa

由表3中两个模型的显著性均为0的结果来看，因为0.00<0.01，即因自变量X的引入，得到的显著性概率值小于0.01，所以很明显的拒绝了总体回归系数为0的原假设，也就是我们要研究的煤炭消费总量与城镇人口数量和社会消费品零售总额之间存在着线性关系。

在判断完成因变量和自变量之间的线性关系后，需要根据t检验值来判断所构建的两个模型中哪些因素被排除。结果如表4所示。

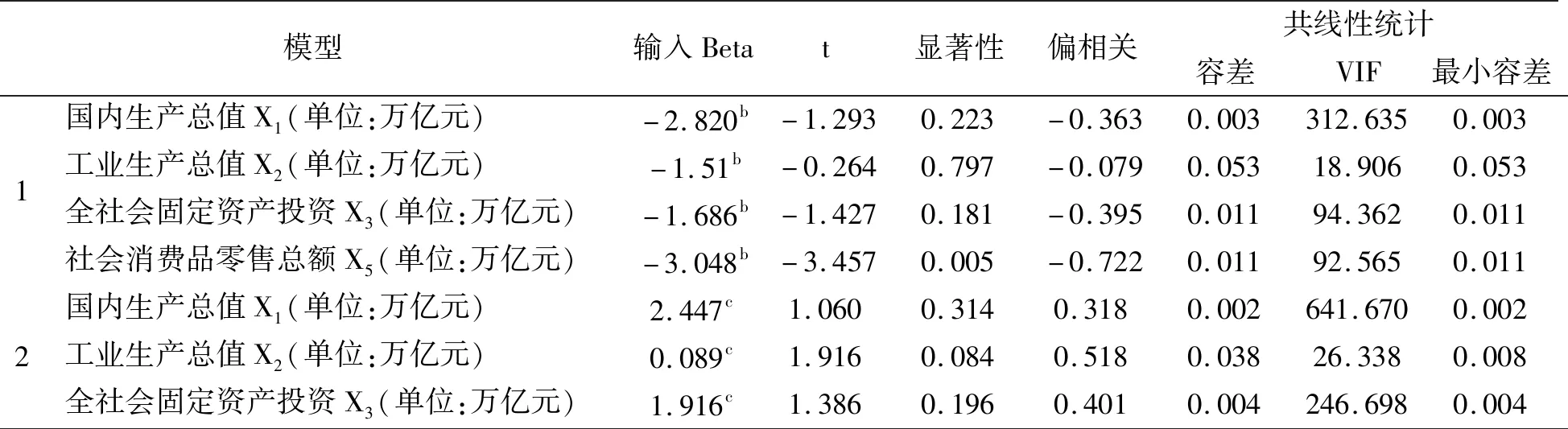
表4 排除的变量a

由表4已排除的变量表中可以得知，模型2中的国内生产总值X1、工业生产总值X2和全社会固定资产投资额X3的t检验值均大于0.05，无法引入线性回归模型，所以予以排除。

根据被排除和被输入的变量，可知对因变量产生影响的自变量因素。根据多元回归模型，需要计算得出这些自变量的系数。结果如表5所示。

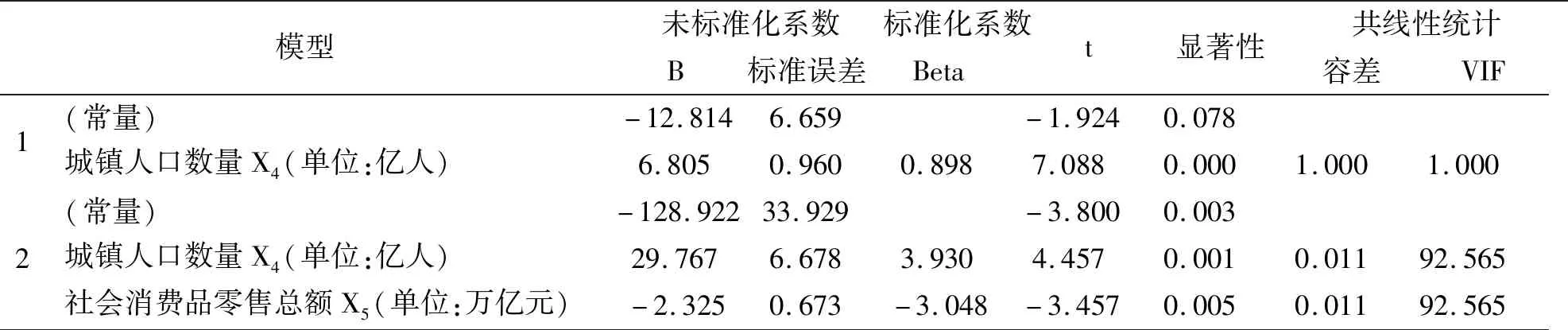
表5 构建的多元回归预测模型系数a

由表5系数表中，模型2中各个因素的显著性均小于0.05，所以我们可以得到多元线性回归方程应该为：煤炭消费总量=-128.922+29.767×城镇人口数量-2.325×社会消费品零售总额。

由共线性统计中，预测变量城镇人口数量X4和社会消费品零售总额X5容差值一样为0.011，且方差膨胀因子VIF值相等，为92.565，虽然VIF值远大于我们通常依据的标准5和10，会出现共线性的可能性很大，但是由于意在预测煤炭消费量，而又由前文可知数据拟合性较好，所以即使存在多重共线性的可能，但是往往不影响预测结果。

在完成构建的多元回归模型后画出直方图，根据直方图结果来判断多元回归预测模型的有效性。结果如图1所示。

图1 多元回归预测模型直方图

由图1可知，预测变量的残差都符合正态分布，说明建立的煤炭消费量预测模型有合理性和准确性。

3.结果检验和验证

根据以上针对数据作出的分析处理，得到了多选线性回归方程如式(2)所示。

Y=29.767X4-2.325X5-128.922

(2)

将所选取数据代入式(2)进行验证，得到的结果差别不大。再将国家统计局公布的2018年城镇人口数量8.64亿人和社会消费品零售总额37.78万亿元代入到式(1)中，可预测得出2018年煤炭消费总量为40.43万吨，与国家统计局公布的2018年全国煤炭消费量39.75万吨差别不大，所以该模型的准确度和可信度是成立的。因国家暂未公布2019年全国煤炭消费量，但是公布了2019的城镇人口数量和社会消费品零售总额，由已构建出的多元回归预测模型估计2019年的煤炭消费量Y=29.767×8.84-2.325×40.80-128.922≈39.36，也就是根据此预测模型，2019年的国家煤炭消费量约为39.36万吨。

四、煤炭消费量的预测

由于煤炭消费总量出现波动，如2009—2017年煤炭消费总量并不是一直上升或下降趋势，所以无法直接根据增长或减少的数量趋势直接预测煤炭消费量。此时，观察城镇人口数量和社会消费品零售总额数据，可以发现二者数据均呈现一直上涨趋势，所以根据二者增长的平均数估计在2030年即碳达峰目标实现时对应的数据。而2004—2017年间我国因基础比较薄弱、各个产业具备巨大发展潜力，又得益于国家政策支持、人民群众的艰苦奋斗，所以在此期间经济发展飞速，城镇化率快速上升，但是在2017—2030年期间，无论是GDP增速还是城镇化的发展势必因经济向高质量发展出现放缓，所以根据实际情况和固有的发展，可以推算出在2030年时，我国城镇化人口数量大约为10亿人，社会消费品零售总额大约为58万亿元。根据预测模型，即煤炭消费量=29.767×城镇人口数量-2.325×社会消费品零售总额-128.922，代入预测数据，可得2030年时我国的煤炭消费总量为33.898亿吨。

由此对比不难看出，煤炭消费量不增反减，由煤炭消费造成的碳排放也已过了峰值。换而言之，碳达峰目标下放到煤炭消费总量的任务在2030年时根据预测是能够完成的。

五、结论与启示

1.结论

根据选取的5个影响煤炭消费量的因素，结合2004—2017年其对应的统计数据，进行了处理和分析，并建立了预测模型。从建立的预测模型观察，城镇人口数量和社会消费品零售总额对煤炭消费量有显著的影响。其中，城镇人口数量与煤炭消费量呈现正相关的关系，社会消费品零售总额与煤炭消费量呈现负相关关系。以模型为基础进行实证，对2018年和2019年的国家煤炭消费量进行了检验和预测，发现误差不大，在可接受范围内，说明了模型据有可信度和准确度。再由已知数据进行推算后代入预测模型，发现在2030年前我国是可以实现碳排放达到峰值即碳达峰的目标的。

2.启示

(1)保持经济的适度持续增长。根据上文所做出的预测模型，不难发现经济发展是促使城镇人口数量和社会消费品零售总额上升的因素，所以要保持经济发展的持续增长，要保证经济发展的模式彻底由粗放式向高质量的方向转变，这对煤炭消费量的控制相当必要。更加注重高质量的经济增长模式会使煤炭的消费量出现下降。

(2)控制能源消费总量。要实现碳中和和碳达峰，现期内要保证煤炭消费的下降趋势。因为煤炭消费总量的下降，会对二氧化碳的排放量的抑制有突出的贡献效果。要保证经济的发展，就不得不在一定程度上依赖能源的消耗，然而可以寻找煤炭的替代产品，以减少对其的依赖程度：如加大对风能、太阳能、水能、生物能、地热能、海洋能等非化石能源的开发利用，努力提高使用效率[14]。

(3)切实提高煤炭清洁利用水平，大力减少散煤消费。在此方面黑龙江省已经提出通过大力削减农村地区、城中村、城市棚户区及城乡结合部散煤使用等方式来降低对散煤的消费，从而减少重污染天气。其他省市地区可以借鉴其经验。

(4)重视科学技术的发展水平。科技是第一生产力。从历史发展的进程来看，科技进步不仅带来了效率的提升，而且还有一定的对资源依赖程度的降低。

(5)推动技术创新水平的进步和产业结构的调整。技术创新水平的进步和产业结构的优化调整会对碳排放的强度起到明显的抑制作用。技术创新要素作用于生产制造业会使生产制造效率得以提升，生产性服务业的附加值会得到提升,从而促使产业结构趋于高级化、合理化。

(6)更好地利用全国碳排放权交易市场。碳排放权交易市场的开市不仅仅意味着人民币的国际化，更是承载了中国人民对绿色发展的美好中国的期待。在碳达峰和碳中和的目标牵引下，通过对煤炭消费总量的研究，势必会使人与自然更加和谐相处。