钛合金薄壁件切削力与残余应力研究

王长清，张毅飞，郑 勇，冯 陶，孟凡明

(1.中国航发哈尔滨东安发动机有限公司， 哈尔滨 150066；2.重庆大学 机械传动国家重点实验室， 重庆 400044)

Ti6Al4V钛合金(TC4)薄壁件具有比强度高、耐高温、耐腐蚀等优点，能够满足工程上减重和增效的要求，被广泛应用于航空航天领域。但由于TC4材料本身弹性模量小、切削效率低等问题，易使薄壁件在车削加工中因切削力和残余应力引起较大的加工变形，难以满足高精度的加工需求。

车削的本质是数控车刀切削刃与工件相互作用产生弹性变形、塑性变形、断裂的过程[1]。刘东等[2]使用不同TC4本构模型进行切削分析，研究发现J-C模型仿真获得的切削力数据与实验结果相吻合。王雷[3]基于ABAQUS对钛合金切削加工进行了二次开发，使用BP神经网络获得了切削力预测公式。王志鑫[4]通过切削力试验获得了切削参数对切削力的影响规律，建立了钛合金切削参数-切削力数学模型。薛林峰[5]基于正交设计试验方法建立了球头铣刀的钛合金切削力模型，并推导出了与实验数据相吻合的切削力公式。Ratchev等[6]建立了薄壁件加工有限元模型，获得了切削过程的切削力变化数据，模拟获得了薄壁件切削变形量。Umbrello等[7]基于有限元并结合神经网络方法提出了轴承钢切削残余应力预测模型，并通过试验对模型进行了验证。刘宁[8]建立了不同工艺参数条件下的钛合金切削力模型，并计算获得了精密切削钛合金的应力场分布情况。

综上所述，尽管已有学者针对薄壁件外圆、内圆车削过程中的切削力和应力分布状态进行了研究，但对于钛合金材料薄壁件端面车削的相关研究却鲜有报道。此外，缺少统一的TC4端面车削的车削力计算标准和工艺参数对钛合金薄壁件残余应力分布的规律研究。本文基于正交试验原理和AdvantEdge软件对不同工艺参数下的TC4进行三维正交切削模拟，确定了影响TC4切削力和工件残余应力的敏感因素，并在不同切削深度和进给速度下对比2种圆角车刀加工时产生的切削残余应力的差异，以期为钛合金薄壁件车削加工引起变形的切削力和残余应力控制提供理论参考。

1 有限元模型

1.1 几何模型

TC4薄壁件端面车削加工过程如图1(a)所示，其几何模型如图1(b)所示，工件绕主轴中心以转速v(m/min)转动，刀具以速度f(mm/r)沿径向进给，切深为d(mm)。当切削半径大于20 mm时，刀具与工件相对运动可以近似为刀具沿工件切线移动，此时薄壁件端面车削可以简化为如图1(c)所示的圆角车削[9]。设定切削长度为L，切削深度为d，进给量为f，工件厚度为w，待切削部分尺寸为h。x方向为切削方向，y为垂直于工件方向，z为进给方向。

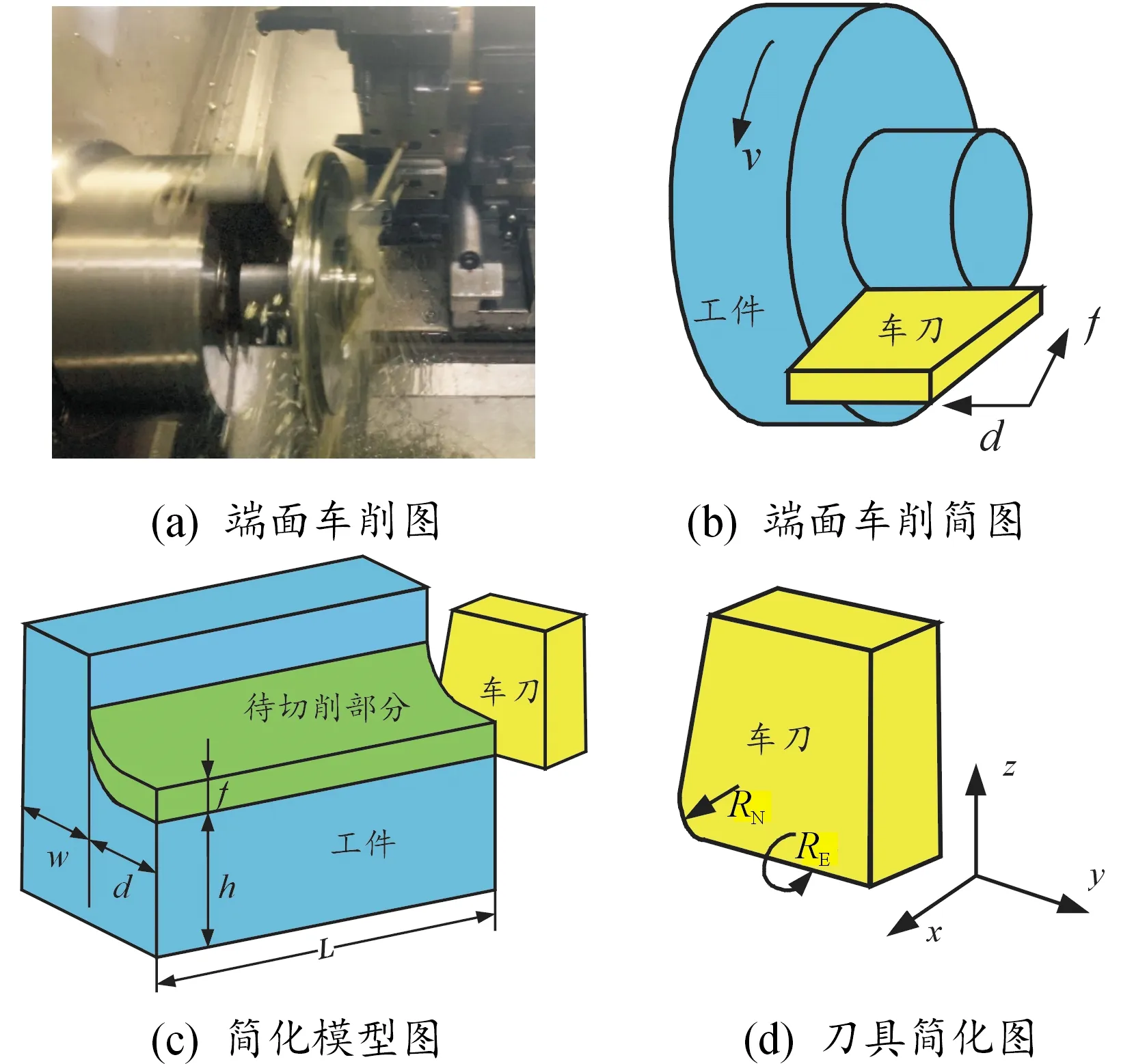
图1 端面车削简化过程

TC4车削加工中多采用35°菱形车刀进行车削，以VCGT160402-HV R0.2车刀为例，其刀具切削刃部分简化图如图1(d)所示。仿真车刀的刀具以VCGT160402-HV为基础进行分析，数控车刀以速度v(m/min)沿x正方向移动。定义刀具绕x轴转动角度为主偏角，绕y轴转动角度为刃倾角角度，绕z轴转动角度为前角。结合实际，为提高分析效率，设定刃倾角和主倾角为0°，进一步分析刀具刀尖圆角半径RN和刀具前角Abr对切削力和工件残余应力的影响。

1.2 网格划分及应力提取

采用有限元方法模拟金属切削过中的切削力和残余应力等状态，其模型如图2(a)所示。使用AdvantEdge软件进行TC4薄壁件车削有限元分析时，不考虑刀具磨损与变形时，将刀具设置为刚体，刀具后面设置全约束固定，工件以切削速度v沿x轴负方向移动，底面设置为y、z方向位移。

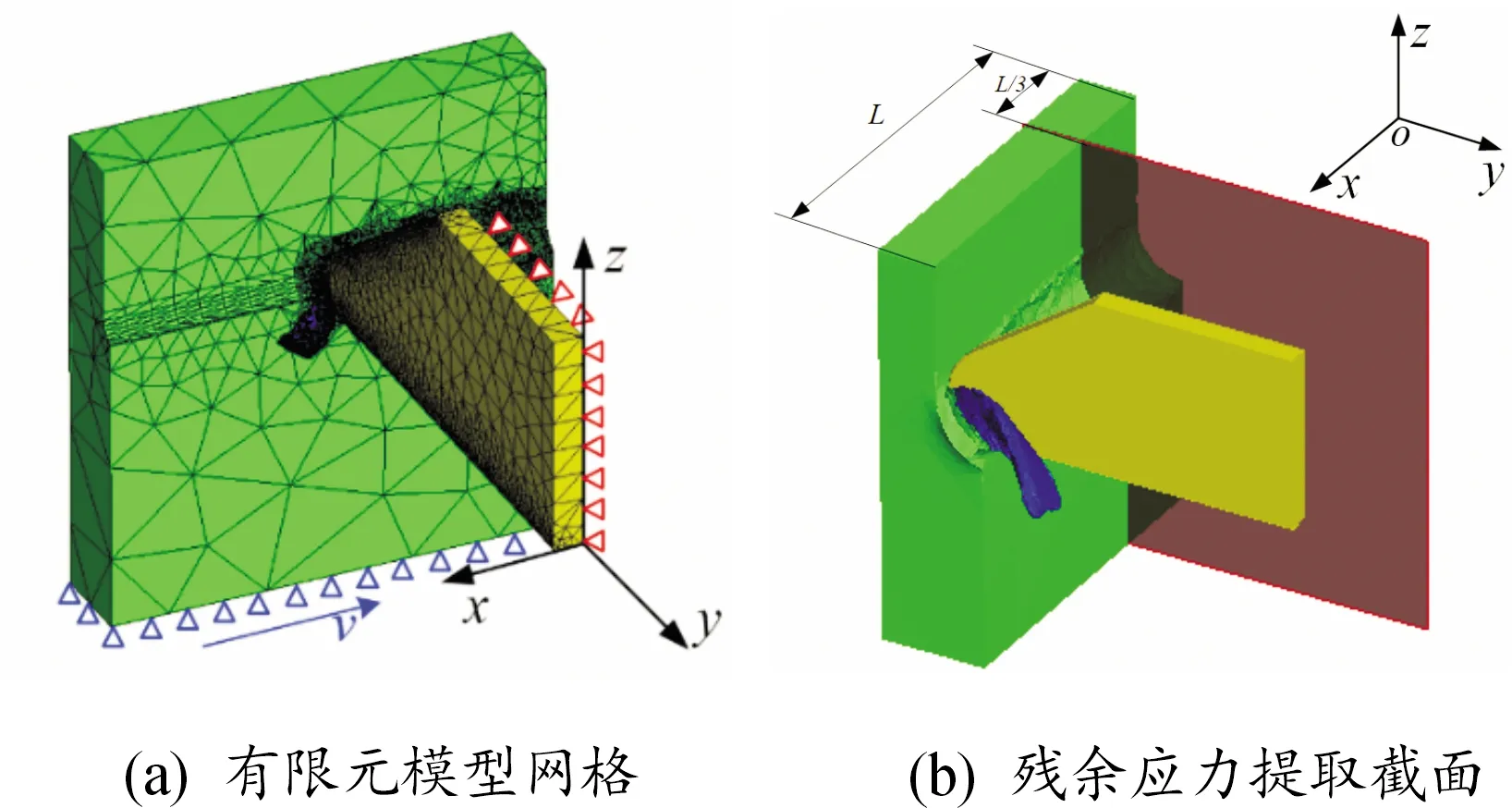
图2 TC4有限元分析

网格单元类型设置为对复杂几何适应性好、划分速度快的四面体网格。为保证计算结果可靠性，对切削区域进行自适应网格细化[9]。考虑到网格参数设置对有限元的求解结果影响很大，虽然加密网格下的求解结果与实际结果符合程度更高，但耗时较长，因此有必要进行网格灵敏度分析以获得合适的网格。如图3所示，最小单元边长减小0.01 mm时，节点数目增加1倍，切削刃细化区域半径为0.05、0.10、0.15、0.20 mm时，单元节点数目依次为8 411、17 899、22 684、46 227，切削力变化均在3%以内。此外，更改网格梯度(过渡区网格最大边与最小边的比值)后，网格数目并未发生明显变化。综上所述，综合考虑计算结果的准确性和计算时间，选择初始节点数目为22 684。

在TC4薄壁件车削有限元分析后处理时，如图2(b)所示，取平行于yOz平面，距离起始切削位置1/3工件长度截面部分提取工件残余应力为薄壁件端面车削残余应力进行分析。

1.3 正交试验设置

正交试验可以利用正交表来安排和分析多因素试验，获得各因素对结果的影响水平。正交表任意1列各水平出现次数相同及任意2列各种不同水平的可能组合均出现的次数相等，这使得部分实验可以包括所有因素的所有水平，所得结果与全面试验结论具有一致性[10]。

将刀具圆角半径、刀具前角、切削速度、进给速度、切削深度5个参数定义为A、B、C、D、E，为研究5种因素对切削力和残余应力的影响，模拟仿真以5因素4水平(L16(54))正交试验为基础进行分析，如表1所示。用TC4材料进行力-热耦合仿真分析，其参数来源于AdvantEdge基础材料库。

1.4 模型验证

在对钛合金薄盘类零件车削加工工程中的切削力、温度及残余应力分析之前，需要对所构建的如图1(c)所示的车削模型进行验证。

根据文献[11]中对TC4钛合金实验和仿真结论，验证时采用的相关仿真参数为：TC4材料AdvantEdge默认模型，切削速度v=200 m/min,切削深度d=0.1 mm，进给速度f=0.1 mm/r，验证结果如图4所示[11]。从图4可以看出，本文所构建的模型与文献中实验测量和仿真结果基本吻合，这说明构建的钛合金薄壁膜盘加工仿真模型的正确性，可用于后续分析。

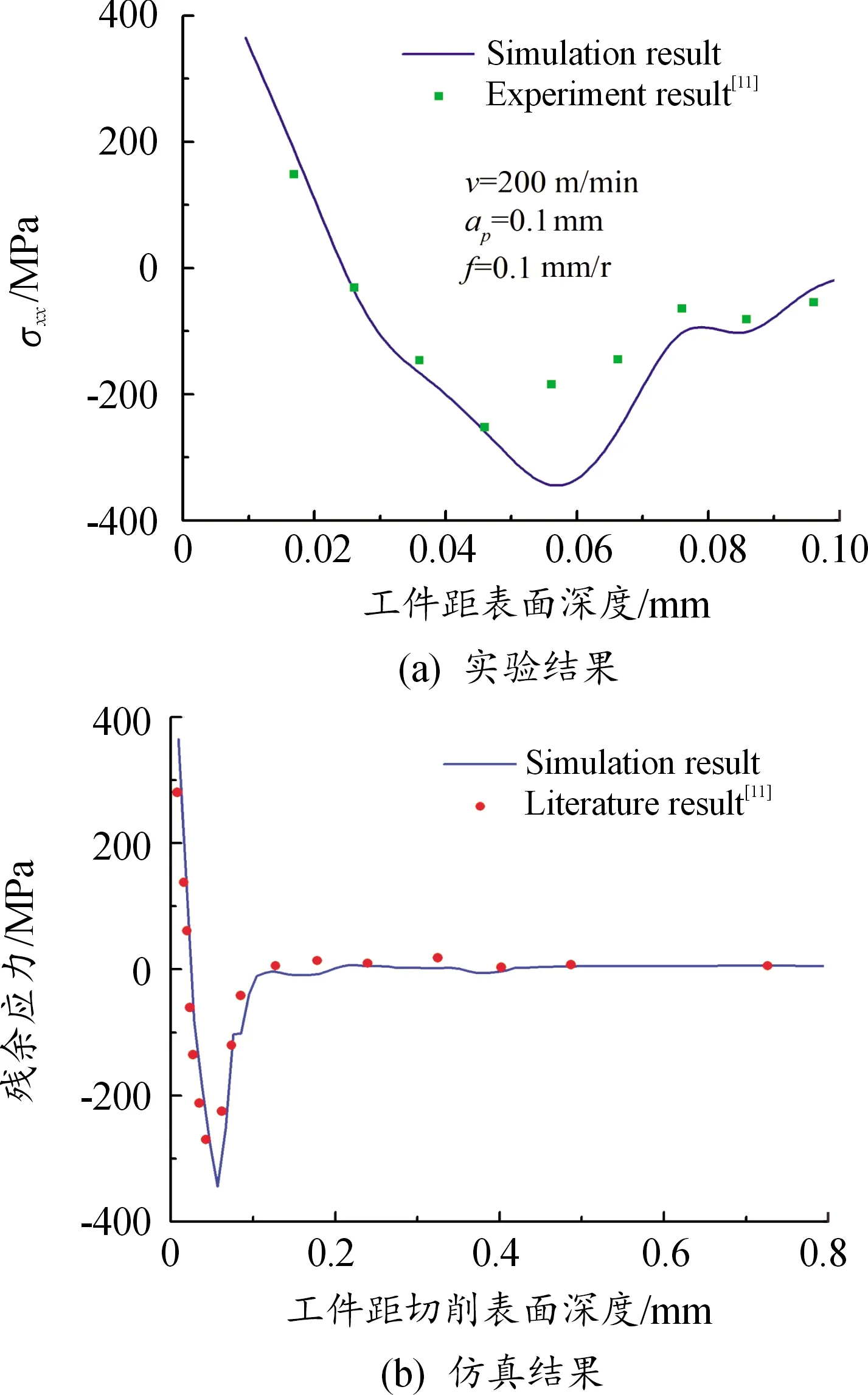
图4 仿真结果与实验结果曲线

2 结果与讨论

采用三维正交切削试验方法模拟Ti6Al4V零件加工过程，采用如图1(c)所示简化模型，仿真参数如表2所示。基于5因素4水平正交实验设计方法，通过使用AdvantEdge进行16组模拟仿真，获得相应的切削力及残余应力，任取正交试验11111条件下仿真结果，如图5所示。其中，Fx、Fy、Fz值分别为通过2×105Hz低通滤波后获得的切削力，并对应提取切削稳定区切削力波动幅值。

残余应力取值位置设定为刀具圆弧与工件接触点中心点位置，获得切削面y轴负方向随工件深度变化的残余应力值。由图5可知，切削力从开始切削到稳定切削阶段经历了逐渐增大并最终趋于稳定波动的过程，工件最大残余应力均出现在工件表面且表现为残余拉应力，靠近工件表面附件处的次表面应力为压应力。

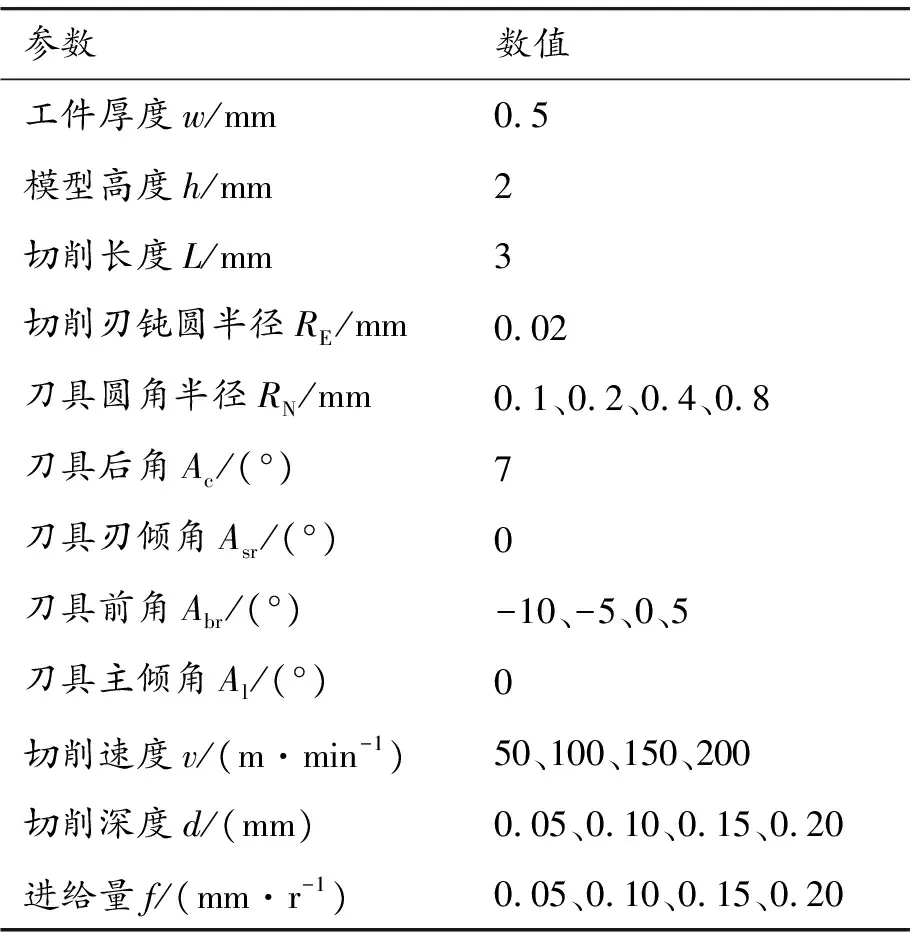
表2 车削几何模型主要参数

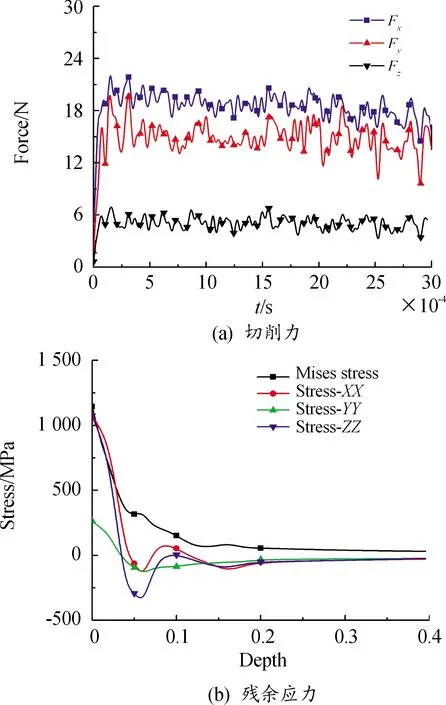
图5 切削力与残余应力结果曲线

2.1 切削力结果

为更好地进行切削力分析，仿真参数数字组合依次表示为表1中A、B、C、D、E5种因素的对应水平，将仿真所得的切削力Fx、Fy、Fz表示为经过2×105Hz低通滤波后所得的“切削力均值±峰峰值/2”进行记录，为记录方便，用“a”代表切削力均值，用“b”代表切削力峰峰值/2，记录结果如表3所示。

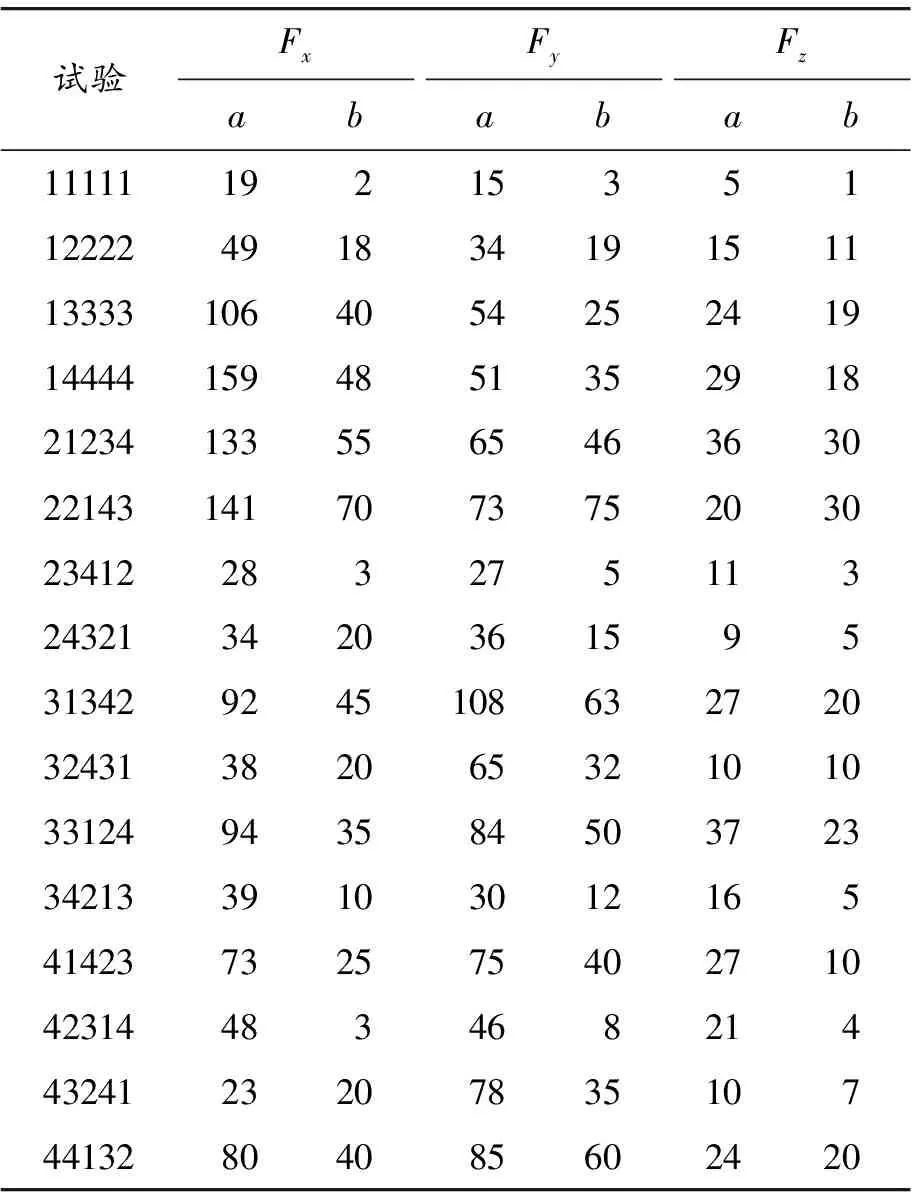
表3 切削力均值及波动值

采用直观分析法对切削力结果进行统计分析，在切削仿真中，考虑了5种因素，每种因素有4种水平，每种水平出现的次数为4次，总仿真次数为16次，Kij表示正交表中因素j水平i对应的平均值，此时Kij可以作为第j列因素水平变化对指标的影响，进一步可计算各个因素的极差R[10]

Rj=maxKij-minKij

(1)

正交试验计算结果如表4所示，极差越大，表明该因素对实验结果的影响越大。从正交分析表结果可以得出：影响主切削力Fx大小的因素由大到小依次为切削深度、进给速度、刀具圆角、切削速度、刀具前角，其中，切削深度对于Fx大小的影响远大于其他4种因素；影响Fy大小的因素由大到小依次为进给速度、刀具圆角半径、刀具前角、切削深度、切削速度；影响Fz大小的因素由大到小依次为切削深度、进给速度、刀具前角、刀具圆角半径、切削速度。

切削力经验公式的一般形式为[1]：

Fa=CadaxfayvazKa(a=x,y,z)

(2)

式中：Ca表示加工材料、刀具材料、加工形式共同决定的修正系数；ax、ay、az分别表示切削深度、进给量、切削速度指数；Ka表示切削前角修正系数。上述系数均根据仿真结果采用待定系数法确定各项参数。

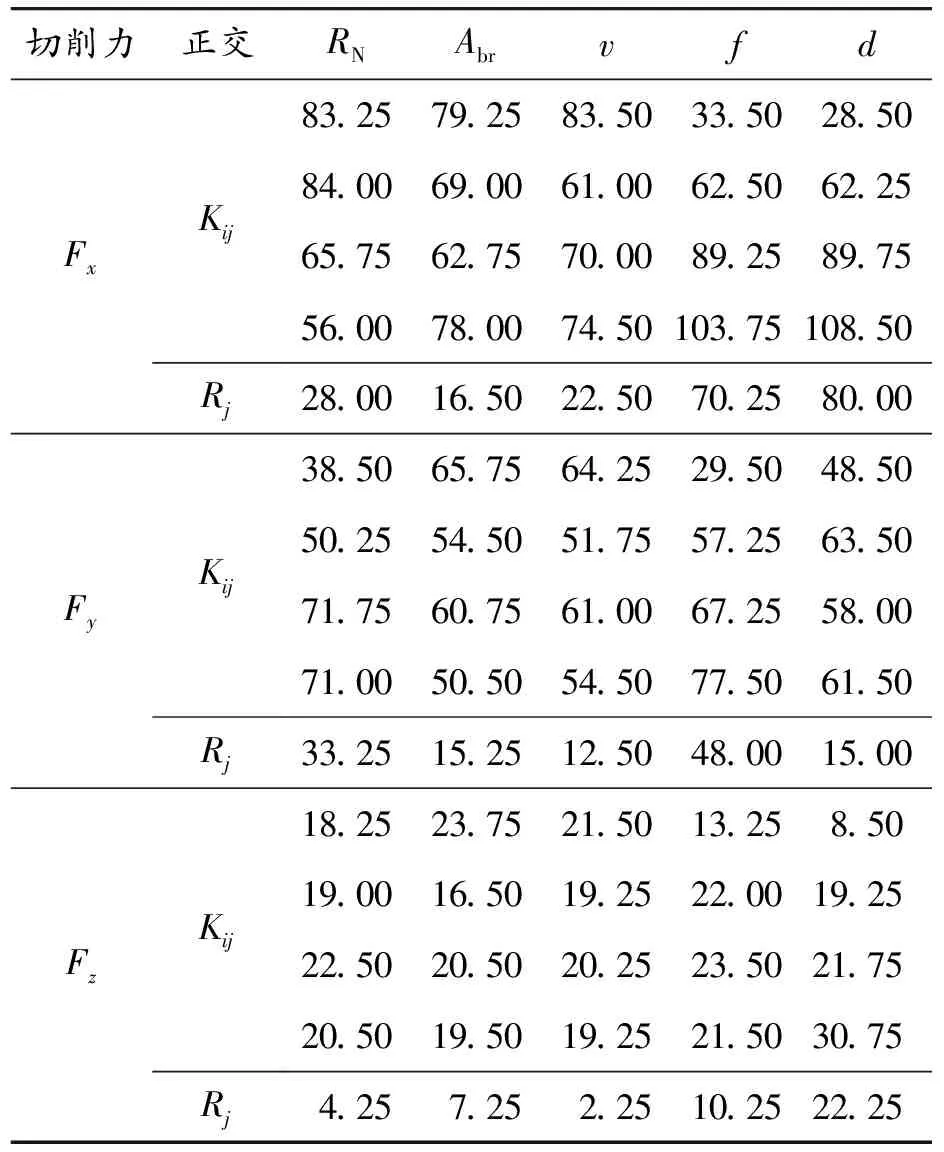
表4 切削力正交分析

图6给出了进给量对切削力的影响，该图中插图为切削力在稳态条件下的均值，其中，切削力时间历程图为仿真数据经过低通滤波获得，滤波频率为1.0×105Hz。由图6可知，随着进给量的增加，主切削力波动幅值增加，由金属切屑形成机理可知，当进给量增加时，切屑呈锯齿状，每段切屑经历弹性变形、塑性变形、断裂3个过程，从而使得切削力发生均匀波动[12]。

此外，随着进给量的增加，切削力的均值增加，但在低进给条件下(f< 0.1 mm/r)，无论刀尖圆角半径如何变化，刀具切削仅由主切削刃和刀具圆角切削刃参与，刀尖圆角半径对主切削力均值影响并不明显。但随着进给量的增大，刀尖圆角半径为0.4 mm时的切削依然由主切削刃和刀具圆角切削刃切削参与，而刀尖圆角半径为0.2 mm的切削则是由主切削刃、副切削刃和刀具圆角切削刃三者共同作用，这导致二者切削力差异变化明显。

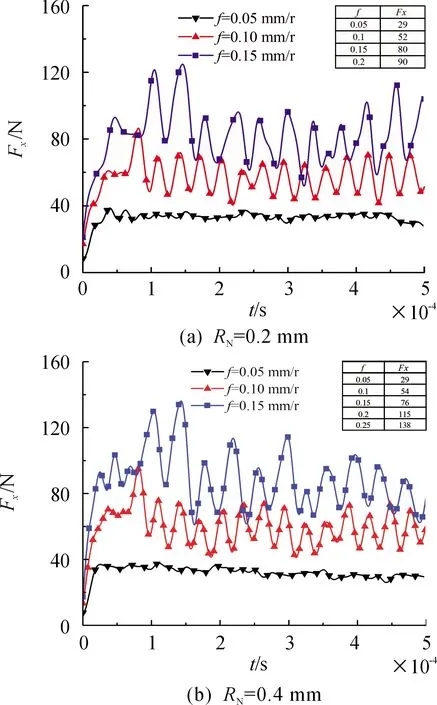
图6 不同进给速度下切削力结果曲线

根据切削力经验式(2)，仅考虑进给量的平均主切削力的经验公式为：

Fx=AffKFf

(3)

式中：Af表示改变进给量时4个固定参数(刃口半径、切削角度、切削速度、切削深度)共同影响下的待定系数，当改变进给量时，Af为定值；KFf为切削力修正系数，可以通过仿真数据进行数据拟合得出。刀尖圆角半径0.2 mm时，Af=510，KFf=1.0；刀尖圆角半径0.4 mm时，Af=584，KFf=1.0。

图7给出了切削深度对切削力的影响，从该图可以看出，随着切削深度的增加，切削力增加，增加刀尖圆角半径对切削力均值影响并不明显，这可能是由于虽然增加了刀尖圆角半径，但其刀具刃口半径并未发生变化，从而切削接触区未发生变化，使得切削力变化并不明显。

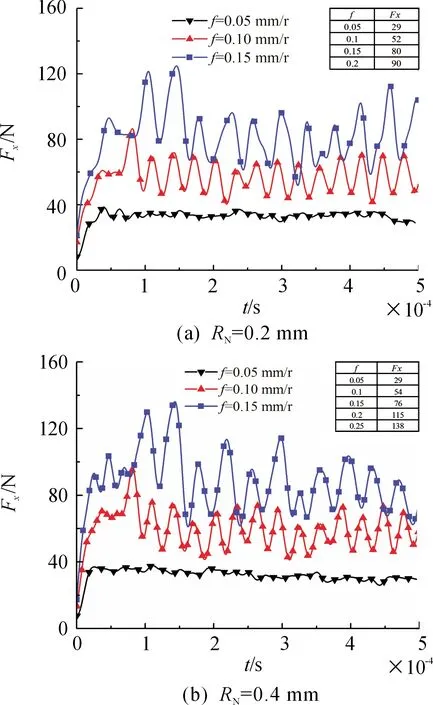
图7 不同切削深度条件下切削力曲线

根据切削力经验公式，仅考虑切削深度的平均主切削力的计算公式为：

Fx=AddKFd

(4)

式中：Ad表示改变进给量时4个固定参数(刃口半径、切削角度、切削速度、进给量)共同影响下的待定系数，当改变切削深度时，Ad为定值；KFd为切削力修正系数，可以通过仿真数据进行数据拟合得出。刀尖圆角半径0.2 mm时，Ad=368，KFd=0.83；刀尖圆角半径0.4 mm时，Ad=388，KFd=0.83。

在确定影响因子较大2个参数的修正因子后，根据正交分析所得切削力结果及线性回归方程，可以获得主切削力的计算公式为：

Fx=3 250d0.83f1n0.02

(5)

经验算，该公式计算主切削力结果均落于仿真切削力波动范围之内，且式中切削深度影响比重大于进给量影响比重，与前文正交分析结果相符。

2.2 残余应力结果

如图2所示，取平行于yOz平面，距离起始切削位置1/3工件长度截面部分提取工件残余应力为薄壁件端面车削残余应力进行分析。获得该截面上的x、y、z向的分应力的最大值、最小值及Mises 应力，其具体数值如表5所示。

表5 残余应力结果

此外，为更好地分析上述5种因素对残余应力的影响权重，本文采用直观分析法对仿真所得残余应力结果进行数据统计，结果如表6所示。通过正交分析表可以看出，各方向及总表层残余应力主要受进给量影响，其次是切削深度和切削速度，而受刀具圆角半径影响并不明显，相似结论也出现在文献[13]中。因薄壁件轴向最薄，故在各向残余应力中，轴向残余应力(y向)是影响薄盘件变形量的主要因素。对内层最小残余应力(残余压应力)，切向与法向应力主要受切削速度影响，而进给量是轴向残余压应力的主要影响因素。

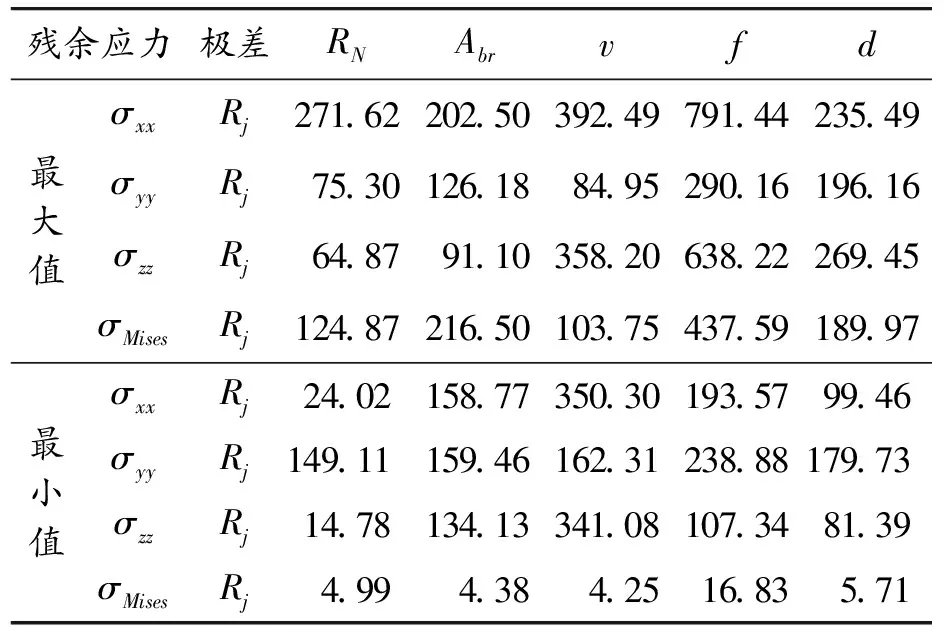
表6 残余应力正交分析结果

薄壁件的切削变形主要受轴向残余应力的影响，图8(a)给出了不同进给条件下RN=0.2 mm刀具车削的轴向残余应力分布规律。从图8(a)可以看出，轴向表层最大残余应力集中于刀具圆弧与工件接触的中心位置，依次为516.7、458.2、419.0 MPa，残余应力向接触区圆弧发散扩展。轴向内层最大残余压应力值逐渐减小，依次为 -519.0、-352.8、-219.5 MPa。而随着进给量的增加，表层残余应力最大值减小，这可能是由于进给量增加后，刀具与工件接触面积增大，从而使得残余应力稀释变小。

为进一步揭示刀尖圆弧与工件接触面积对残余应力的影响，图8(b)给出了刀尖圆弧RN=0.4 mm时不同进给量条件下的残余应力分布，研究发现表层最大残余应力同样集中于刀具圆弧与工件接触的中心位置，同时刀尖圆角增加后轴向残余应力略有减少，与前述结论符合。

但选用刀尖圆弧较大的刀具后，表层残余应力最大值由待切削部分向已完成的工件表层偏移，在此条件下产生的残余应力释放时将会严重影响工件加工精度。因此，使用小刀尖圆角刀具适合进行小进给量的精加工工序，可以有效减少工件成型部分的残余应力。

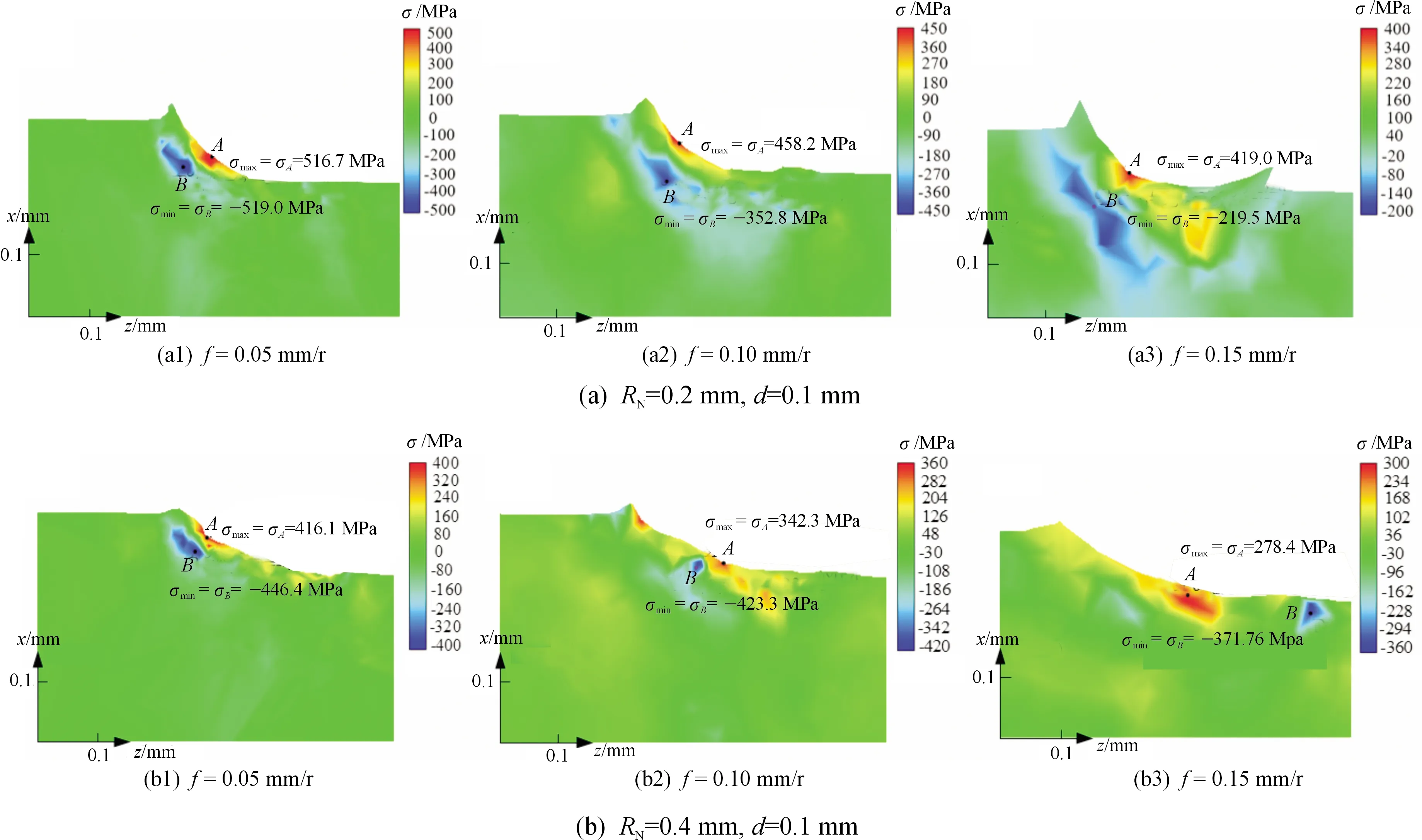
图8 不同进给量条件下残余应力分布

图9(a)给出了不同切削深度条件下的轴向切削残余应力分布状态，由该图可以看出，随着切削深度的增加，切削力增大，表层残余压应力和内层残余压应力的绝对值增大。此外，表层残余应力最大值的位置随着切削深度的增加由工件与待切削部分相接直线逐渐向待切削部分偏移，此时使用实验测量获得的残余应力结果可能以压应力为主[14]。

图9(b)给出了刀尖圆弧0.4 mm时不同切削深度条件下的残余应力分布，对比图9(a)可知，相同条件下，增加刀尖圆弧后轴向残余应力减小，且增加切削深度后，残余应力出现位置向待切削部分偏移的情况，这是由于增加刀尖圆弧后刀具几何形状发生改变，刀具切削刃与工件接触中心位置发生改变所致。但对比图9(a1)和9(b1)可以发现，切深较小时具有大刀尖圆角的刀具会对工件成型部分留下更大的残余应力，这对控制加工变形不利。因此大圆弧刀具更适宜进行大切削深度条件的粗加工，一方面可以减少出现于工件表层的残余应力，另一方面出现于待切削区部分的大残余应力对毛坯和粗加工的影响较小。

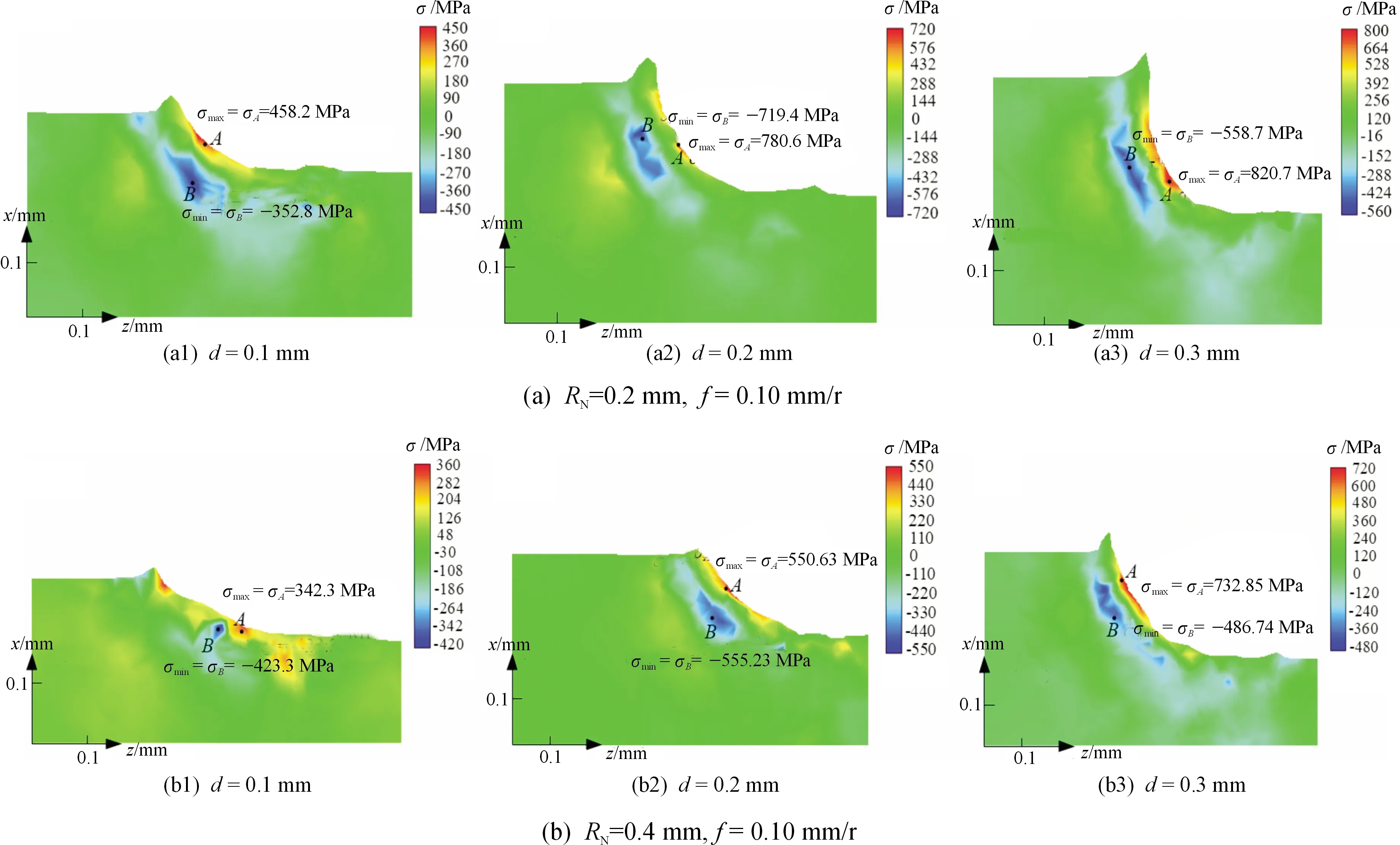
图9 不同切削深度条件下残余应力分布

2.3 钛合金薄壁件加工精度实验评价

基于上述模型所得工艺参数对切削力与残余应力影响结果，选择刀尖圆角半径为0.2 mm的35°菱形数控车刀对如图10(a)薄壁盘类工件进行加工，该工件最薄位置仅为0.45 mm。选择切削深度为0.1 mm，进给速度为0.2 mm/r时，成品件采用如图10(b)所示的G80-C三坐标测量仪测量。发现该工况下的工件双面的加工变形量最小，如图11所示，工件轮廓度有效控制在±0.04 mm内，且部分区域可以达到0.02 mm以内，说明该工况条件下的切削力和残余应力被控制在符合弱刚性薄壁件的加工需求的范围内，工件加工变形较小，满足加工精度要求。

图10 三坐标测量

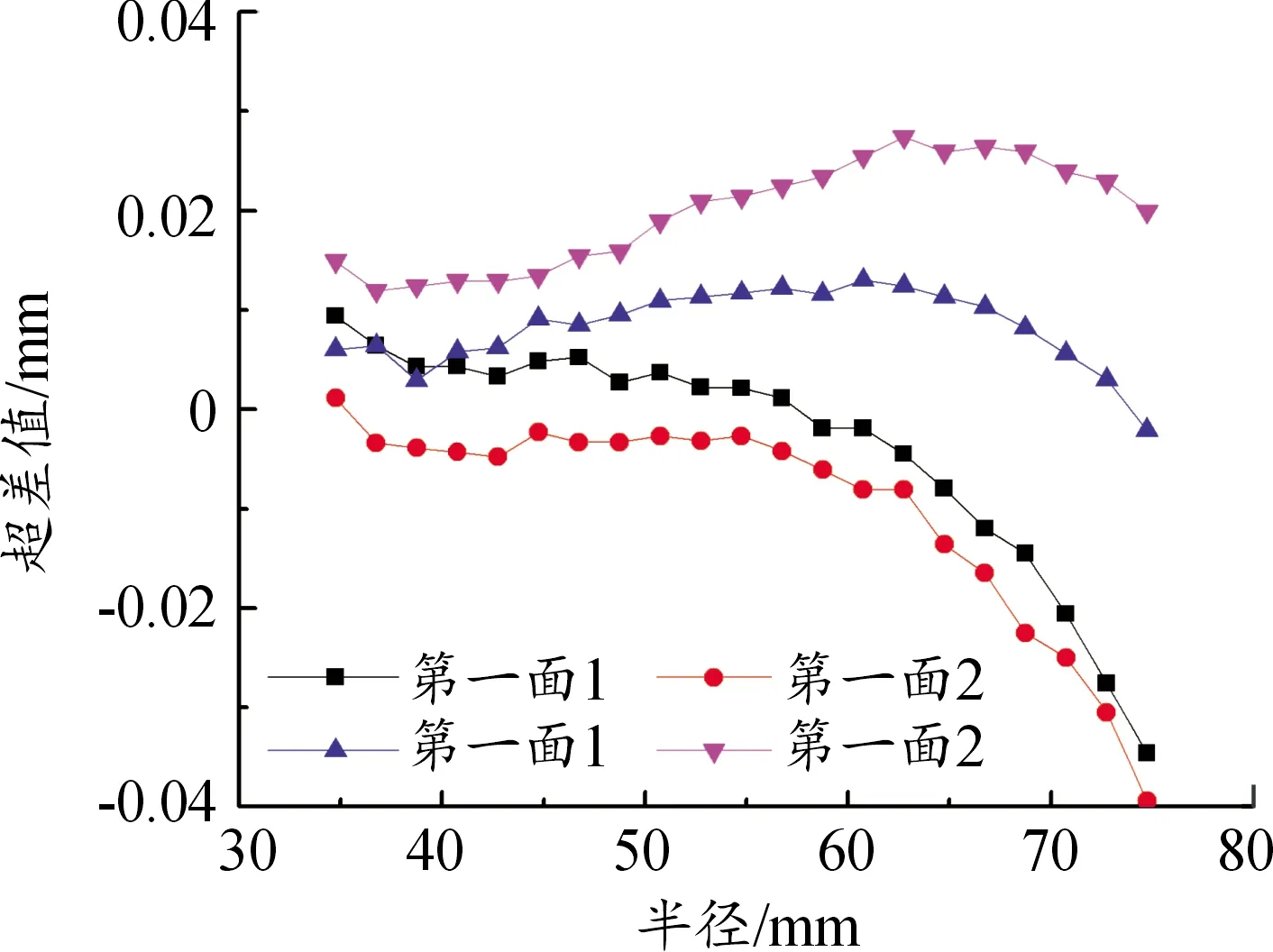
图11 轮廓度测量曲线

3 结论

基于正交分析理论，开展刀具圆角、进给速度、切削深度等工艺参数对钛合金TC4薄壁件切削力、残余应力的影响规律研究，拟合出了钛合金端面车削的切削力经验公式，获得了不同工艺参数下的切削力及残余应力分布状态，相关结论如下：

1) 影响钛合金薄壁件端面车削切削力因素主要为切削深度和进给量，而刀具角度、切削速度、切削速度对切削力的影响较小；

2) 钛合金薄壁件端面车削的轴向表层残余应力大小主要受切削进给量影响，表层轴向残余应力最大值位于刀具与工件接触的中心位置；

3) 粗加工时选择大圆角半径车刀进行大切深车削，半精加工及精加工时选择小圆角半径低进给量车削，可改变切削残余应力分布位置，减少工件残余应力和加工变形。