基于蚁群算法的多车型物流车辆调度研究

段丽妮，阚龙营 DUAN Lini,KAN Longying

（沈阳化工大学 经济与管理学院，辽宁 沈阳 110000）

0 引 言

车辆路径问题（VRP）由Dantzig和Ramser于1959年首次提出，它是指一家配送企业向一定数量的客户进行货物配送，各客户拥有不同的货物需求，由配送中心指派车队进行货物配送，组织合适的配送路线，使客户的需求可以得到满足，在一定的约束下，可以达到配送成本最小、配送时间最短等目标。目前，车辆路径规划问题不断发展，在考虑实际情况下增加约束满足目标，求解此类问题的方法也在不断改进创新。

对于车辆路径规划问题的研究，刘虹庆和王世民在强化学习的基础上分别对小规模和大规模的VRP问题进行研究，小规模问题应用了时间差分模型，大规模问题应用蒙特卡洛模型，为车辆路径问题的研究提出了新思路；邓友均和穆云飞等考虑了电动汽车在配送中的换电成本、车辆损耗成本和慢速放电成本构建基于客户满意度的多目标模型，并应用非支配排序遗传算法验证了模型有效性；姚佼和邵楚薇等建立上层为考虑应急救援车辆的调度费用成本和下层考虑救援车辆在途时间的双层规划模型，降低了调度成本和行程时间；胡林和周登辉等提出改进的A*算法，在信号灯转换概率和电动汽车的能耗模型基础上，使得电动汽车在起止点通过的路径能耗最优；李得成和陈彦如等研究了电动车和燃油车的混合车辆路径规划问题，在获得初始解之后设计分支定界算法获得最优解，提出关于车辆路径规划相关建议；杜茂和杨林等提出了一种基于时空动态交通信息的路径规划算法，在广义回归网络和A*算法基础上，可以使得规划后的路径耗时最短、更加节能；贺智明和郑丽等提出一种自适应动态搜索蚁群算法（ADACO），并将其与AACO和ADCO以及ACO算法进行比较，在算例仿真的结果中表明其提出的算法路径规划的配送成本和时间开销都大幅度减少；罗子涵和彭旷等提出一种分层改进A*算法来解决雨天路径规划问题，减少车辆在雨天道路积水时的风险并提高行车效率；刘晓欢和张德干等利用改进的粒子群算法对模糊神经网络的参数进行了优化，其提出的算法有效地解决了智能驾驶车辆路径规划问题。

蚁群算法在路径规划中的应用，王庆和徐海明等在传统蚁群算法收敛速度慢、容易陷入局部最优的基础上进行改进，并将其应用在无人机航迹规划，算法增加了蚁群全局搜索能力和效率，更好地适应了无人机的飞行需求；胡佳斌和王祥澍等通过差异化更新信息素并对启发函数改进，设计了优化的多步长蚁群算法，提高了算法的收敛速度；胡蓉和陈文博等针对城市中心拥堵情况严重问题，提出一种知识模型的学习型蚁群优化算法，算法引入了多邻域局部搜索增强了搜索深度和算法性能；曹建秋和徐鹏等以蚁群算法为基础，并将粒子群算法中的适应度作为启发值引入蚁群算法的信息素更新中，使用贪心策略优化算法的选择，利用A*算法进行随机初始化，有效地提高了算法的收敛速度和求解质量；刘博省和毛范海等在解决生产规划和排程问题时，将蚁群算法与禁忌搜索算法进行互补结合，提出蚁群禁忌搜索融合算法来解决车间调度问题；王原和陈名等将深度学习方法应用至蚁群算法中，使得蚁群算法可以利用深度强化学习提取启发式信息，并利用经典的TSP问题进行验证，结果表明该算法有良好地求解优势和稳定性。

学者们对于物流车辆路径优化问题已设计多个领域，包括冷链物流、电子商务、零售企业等，将VRP进一步发展，建立了具有容量约束、软硬时间窗约束或者顾客满意度约束的模型，并使用算法进行求解和实例仿真，为现实生活中的路径优化提供良好的思路；但是目前的研究很多是基于单一车型的研究，而在实际的生活中，通常会出现多车型进行物流配送，本文考虑实际情况中的多车型问题，研究物流车辆配送路径优化问题。

1 模型建立

考虑物流运送中的成本约束，本文仅考虑单一配送中心，并做了以下假设：

（1）只有一家物流企业提供配送服务；

（2）每个客户被访问且仅访问一次；

（3）物流企业有多种车型车辆进行配送，不同车型的车辆出车成本和载重量不同；

（4）不同车型车辆配送数量限制不同，组合车型和单车型车辆配送数量限制不同。

各参数与集合定义如表1所示：

表1

根据参数信息等，构建的数学模型如下：

其中：目标函数为总成本最小，包含了运输成本和出车成本两部分；约束条件为式（1）至式（5），式（1）表示车辆的容量约束，式（2）表示车辆运输的总时间约束，式（3）表示每种类型车辆数量限制，式（4）和式（5）表示每个客户点仅被一种车型访问一次。

2 蚁群算法

车辆路径规划问题属于NP难问题，求解此类问题通常采用的方法有两大类，分别是：精确算法和启发式算法。精确算法通常是指运用运筹学中的线性规划、非线性规划等数学规划的技术来进行求解小规模的确定性VRP问题，而对于较大规模的复杂问题时，通常采用启发式算法来进行求解，目前应用的启发式算法种类有很多，本文基于蚁群算法的收敛效率和求解速度以及其不易陷入局部最优解的特点，选择蚁群算法来进行求解。

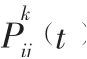
其中：Δτ表示所有蚂蚁在城市与连接路上释放的信息素浓度总和。ρ为轨迹的持久性，1-ρ为轨迹衰减度，表示消减程度。为正常数，L为蚂蚁在此次运动中所走路径的长度。用蚁群算法求解车辆路径优化问题的算法流程如图1所示，具体步骤的含义如下：

图1 蚁群算法步骤

步骤1：对相关参数进行初始化，包括蚂蚁初始化群规模、信息素因子、启发函数因子、信息素、挥发因子、信息素常数、最大迭代次数等，以及将数据读入程序，并对数据进行基本的处理，如将城市的坐标位置，转为城市间的矩阵。

步骤2：随机将蚂蚁放于固定出发点，对每个蚂蚁计算其下一个访问城市，直至所更新信息素表有蚂蚁访问完所有城市。

步骤3：计算各个蚂蚁经过路径的花费，记录当前迭代次数中的最优解，同时对各个城市连接路径上的信息素浓度进行更新。

步骤4：判断是否达到最大迭代次数，若否，则返回步骤2，否则终止程序。

步骤5：输出程序运行结果，并且根据需要输出蚁群算法运行结果，包括最优路径规划和最低成本等。

3 算例仿真

某物流企业拥有多种不同类型的车辆进行物流配送业务，该公司在一天内的配送业务（包括物流企业及客户的坐标位置及客户需求量）如表2所示，其中物流企业的标号为0，到达客户点卸货验货耗时规定为15min，车辆行驶速度为60km/h，可用车辆的载重类型为4吨、6吨、8吨，出车成本及距离成本如表3所示。

表2 物流中心、客户坐标点集合及各客户需求量

表3 车辆类型及信息

利用Python软件进行模拟仿真计算，设各参数分别为：蚁群数量为100，α、β无限接近1，在仿真计算之后，得出组合车辆最优成本为1 874.63元，具体车辆路径如表4所示，并对单车型车辆进行仿真计算，规定单车型4吨车辆为6辆、单车型6吨车辆为4辆、单车型8吨车辆为3辆，得出单车型车辆配送成本及路径分别为：单车型4吨车辆配送成本2 013.12元，路径为0-8-4-12-0、0-1-2-27-6-15-9-0、0-13-11-0、0-7-18-3-16-0、0-10-0、0-14-5-0；单车型6吨车辆配送成本2 196.21元，路径为0-5-4-2-17-14-18-0、0-3-11-8-10-7-1-16-9-0、0-12-13-0、0-15-6-0；单车型8吨车辆配送成本2 652.96元，路径为0-5-4-17-15-16-14-1-9-2-0、0-6-11-0、0-12-13-18-10-3-7-0。多组合车型配送成本明显低于单车型配送成本。

表4 组合车辆路径规划

4 结论及意义

物流运输合理规划可以使得企业降低成本、提高效率、提高顾客满意度，从而增加企业的经济效益。本文通过建立多车型物流规划配送模型，以配送成本最低为目标，加入时间约束和车辆载重约束等，并使用蚁群算法对模型求解。求解结果表明多车型组合配送成本低于单车型配送成本且具有较大优势，为物流企业配送运输提供一定的参考价值。此外，本文的研究未考虑多车场及算法的组合优化改进，在未来可以进一步研究。