曲线梁桥的简化分析方法及地震易损性研究

刘彦 田彦

摘要 曲线梁桥往往集中分布于城市交通枢纽位置，其结构破坏会造成交通流量的中断，阻碍城市交通系统的稳定运行。文章结合武汉市某6跨连续曲线梁桥采取OpenSees构建简化有限元模型，针对双柱墩曲线梁桥1号桥墩、2号桥墩进行纵横桥向的地震易损性曲线绘制，并对该结构纵横向结构易损特性进行比较，结果表明，1号桥墩具备更大的损伤概率，且纵桥向桥墩损伤概率要明显高于横桥向，设计中需要加强纵桥向桥墩的保护。

关键词 曲线梁桥;地震易损性;纵横桥向

中图分类号 U442.55 文献标识码 A 文章编号 2096-8949（2022）07-0160-03

0 引言

城市大跨度曲线连续梁桥作为公路交通的重要组成部分，对于衔接区域产业经济具有显著社会意义，地震活动极容易对梁桥造成结构损伤，继而造成交通中断及生命财产安全，严重的梁桥地震破坏还会引发次生灾害。基于此，科学合理地开展梁桥地震易损性研究对于梁桥稳定安全运营具有不可忽视的重要性，能够为梁桥抗震设计加固提供必要基础，重要结构的地震易损性分析对于实现城市公路交通网络的整体评估具有工程价值。

1 梁桥震害特征分类

不同强度地震动情况下，连续曲线梁桥的破坏形式及破坏结构具有较大差异性，依据国内外近十年的梁桥地震破坏特点，梁桥的地震破坏可以依据其产生原因具体分为以下几类：梁体破坏及移位、支座破坏、桥面系破坏、桥头路堤沉陷、次生灾害及桥墩桥台破坏。

2 有限元簡化分析

2.1 工程概况

武汉市某6跨连续曲线梁桥是当地交通网络的重要结构，桥面设计宽度为13.26 m，跨度达到了270 m，平面曲率半径为900 m。上部设计中主梁结构为钢-混箱梁，截面为等截面，混凝土强度C50，下部结构桥墩设计则采取双柱圆墩，桩基础为钻孔灌注桩，混凝土设计强度C30。桩基础、桥墩结构内部纵向配筋分别为60根32 mm、28 mm的HRB335钢筋，整体式桥台构造，矩形截面盖梁，桥台、盖梁都设置了4个橡胶支座，建设场地特征周期0.45 s、Ⅲ类[1]。

2.2 简化模型构建

该文采取OpenSees构建该项目的简化模型，建模过程中，对于梁桥上部结构主梁主要采取梁单元elasticBeam Column进行模拟，下部结构桩基、桥墩则采取梁单元dispBeam Column模拟;混凝土模拟采取Concrete02本构模型，钢筋模拟采取Steel02本构模型;主梁边界约束受到台后填土、桥台的纵横向作用，其模拟采取0长度单元的材料Hyperbolic Gap进行设置;0长度线弹性单元模拟橡胶支座;桩土相互作用模拟则采取0长度桩土弹簧单元;土层的0长度单元进行水平向、桩竖向、桩底竖向土压力-位移关系模拟分别选取PySimple1、TzSimple1、QzSimple1材料。

3 地震易损分析

3.1 地震动选取

地震波的研究获取主要通过以下两种方式：地震波人工合成、地震波实际记录。两种方式获取的地震波难以适应梁桥抗震参数需求，人工合成地震波主要采取回归模型及三角级数进行合成，较为匹配设计要求反应谱，但是考虑到强随机性，人工合成地震波就具备明显局限性。依据既有地震活动监测系统，可以对地震动进行较为方便的记录及监测，现存的较大数据库为梁桥抗震设计提供了极大便利。该文所针对项目位于武汉市区，由《中国地震动参数区划图附录A1》可知该项目的地震动峰值加速度为0.15 g，梁桥设计以7度设防，场地Ⅲ类。项目采取PGA为地震动强度指标，采取反应谱匹配技术，进行PEER的地震动筛选工作，获取百条满足要求的地震动，并通过IDA分析方法进行地震动调幅，获取地震动0.1～0.15 gPGA之间的相关数据，继而进行关键易损结构的非线性动力时程计算，最终得到桥墩构件的地震动最大响应[1]。

3.2 结构损伤指标确定

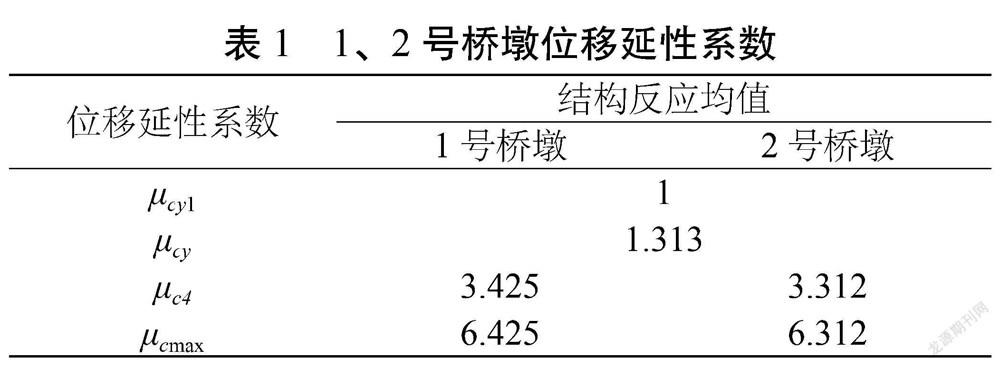
项目桥墩结构损伤指标主要选取为墩顶位移延性，通过上述简化有限元模型进行1号、2号桥墩的地震易损性研究，不同桥墩的位移延性系数如表1所示。

3.3 易损曲线绘制

地震易损曲线绘制流程如下：项目对梁桥结构进行百条地震动数据输入，获取不同地振动下的1、2号桥墩墩顶位移及相关延性系数;开展地震动加速度峰值、位移延性系数的对数回归分析，其关联性满足线性，且结构反应概率函数符合正态分布规律，可以采取墩顶位移延性系数表征桥墩结构的承载强度，桥墩承载强度也满足正态分布。桥墩易损性曲线主要表现为不同PGA情况下桥墩动力响应超过承载强度的概率，如式（1）所示[1-2]：

（1）

式中，——正态分布函数;

βc、βd——标准差;

、——结构承载能力均值、结构反映均值。

通过HWang[3]的研究结果，设定为0.5，桥墩结构在不同地震动加速峰值下的易损概率曲线绘制公式如式（2）[1-2]：

（2）

式中，A、B分别表征指标（位移延性系数、地震动加速度峰值）对数线性曲线的斜率、截距。

4 易损曲线分析

4.1 纵桥向

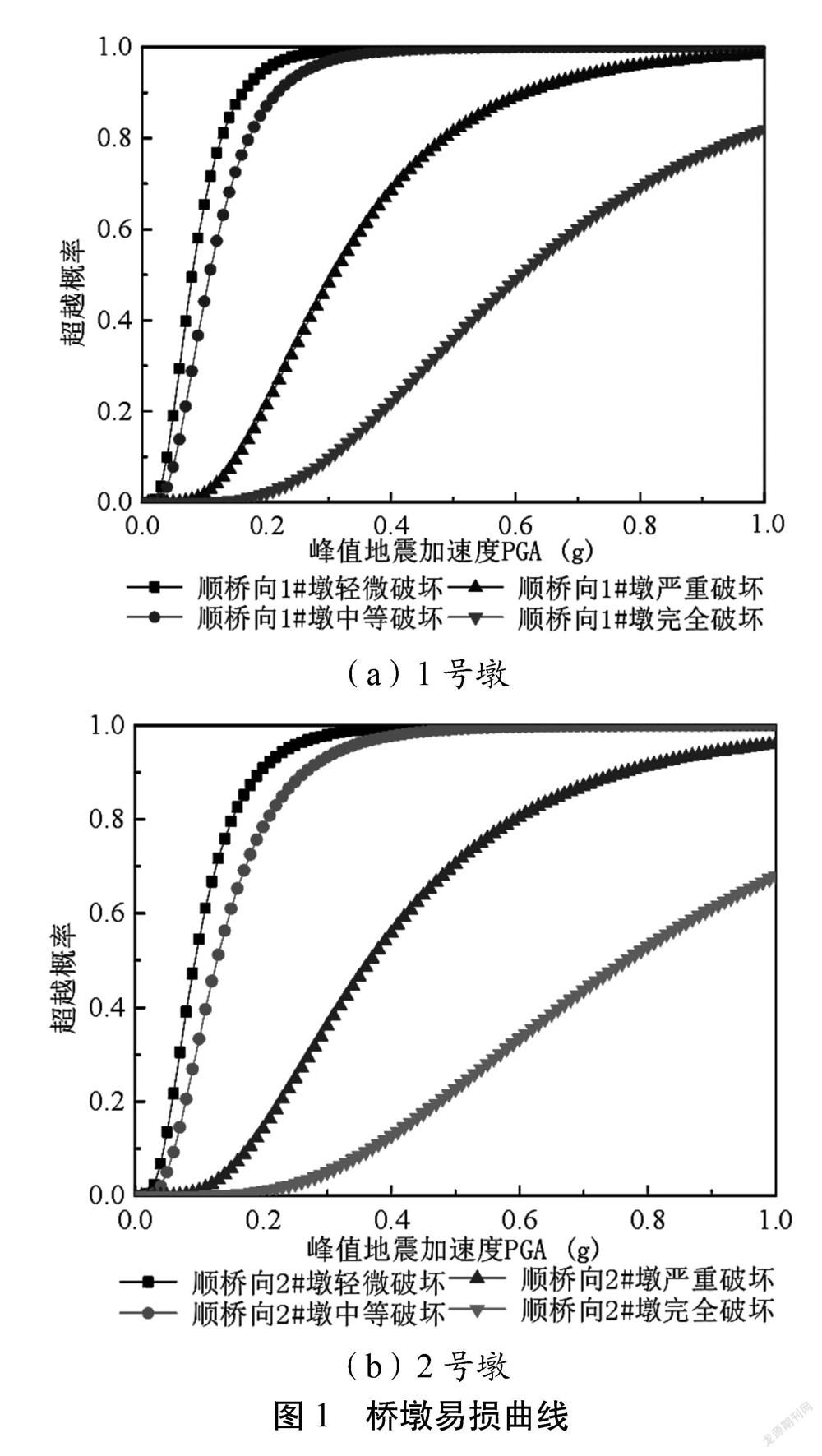
项目对1、2号易损桥墩进行地震响应分析，纵桥向地震动数据输入后获取相应位移延性、地震动峰值加速度的对数回归统计，易损曲线图如图1所示。1号桥墩易损曲线表明，中等及轻微破坏状态下桥墩易损曲线变化趋势较剧烈;PGA0.05 g、烈度6度作用下，该桥墩轻微破坏的概率达到了19.01%，中等破坏概率则达到了7.71%;PGA0.1 g、烈度7度作用下，中等破坏概率达到了44.11%，轻微破坏概率则达到了65.51%，严重破坏概率达到了2.22%;PGA0.2 g、烈度8度作用下，中等破坏概率达到了87.01%，严重破坏概率达到了21.51%，轻微破坏概率达到了95.32%;PGA0.4 g、烈度9度作用下，完全破坏概率达到了22.23%，严重破坏概率达到了69.12%。2号墩在烈度6度作用下，轻微破坏概率为13.51%，中等破坏概率达到了5.33%;7度烈度下，中等破坏概率为33.12%，轻微破坏概率为54.51%;8度烈度下，轻微破坏概率91.02%，中等破坏概率78.11%，严重破坏概率14.31%;9度烈度下，完全破坏概率12.72%，严重破坏概率56.33%[4-6]。

项目将不同桥墩的易损曲线进行对比，纵桥向地震动下2号墩相对于1号墩的损伤程度较轻，且损伤概率要小于1号墩;2号墩、1号墩具备差异性较小的等效屈服曲率及首次屈服曲率，两个桥墩产生中等、轻微破坏时具备较为一致的易损曲线;2号墩产生轻微、中等破坏的概率均要小于1号墩，2号墩在完全及严重破坏状态下产生的概率也要小于1号墩;地震动强度的增大会促使1号墩趋向于完全破坏状态，这主要是2号墩柔性相较于1号墩要更为优越，地震力承担部分相对较小[4-6]。

4.2 横桥向

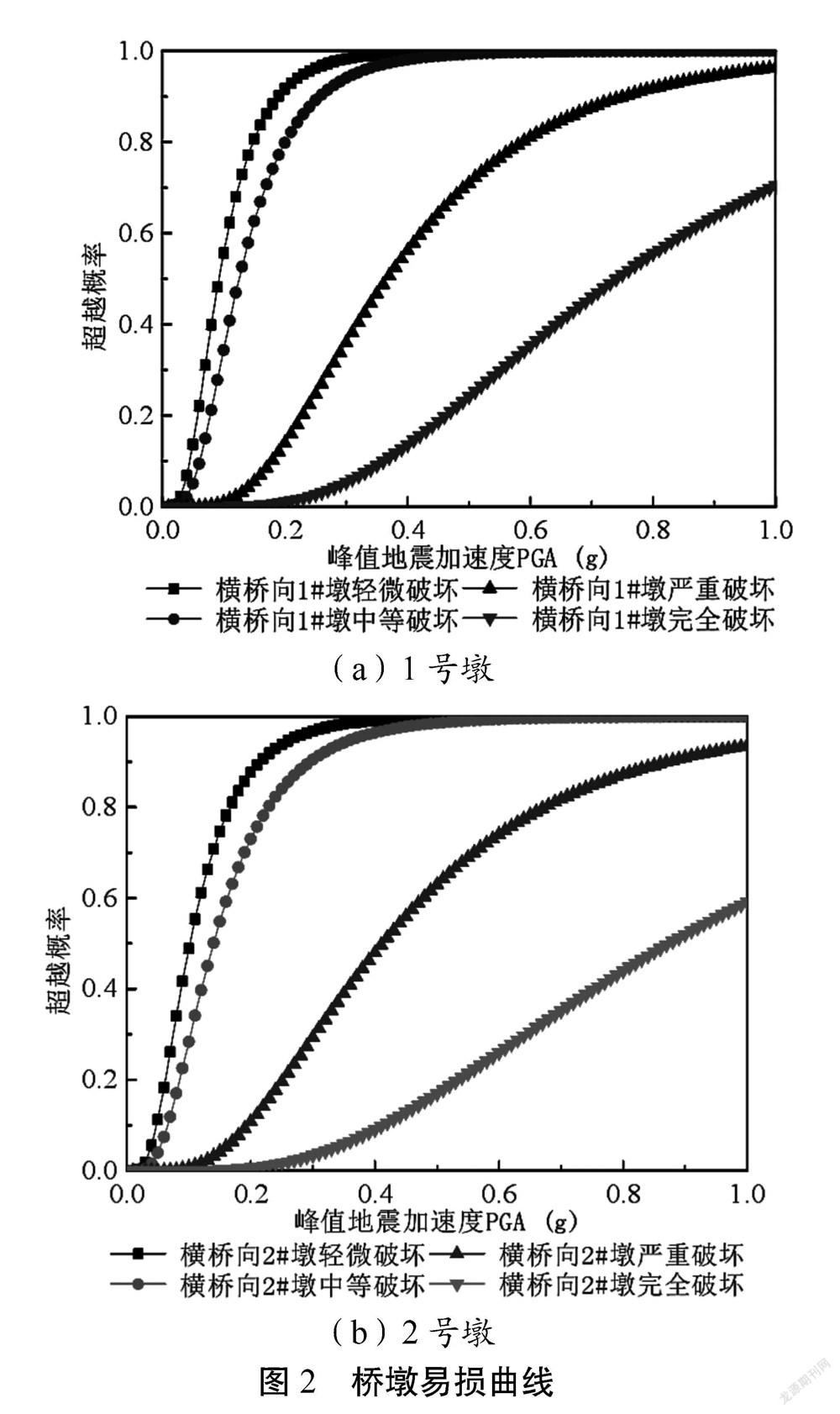
横桥向的地震动数据输入后可以获取相应桥墩的位移延性、地震动峰值加速度对数回归曲线，桥墩的易损曲线如图2所示。

1号桥墩易损曲线表明，PGA0.05 g、烈度6度作用下，该桥墩轻微破坏的概率达到了13.71%，中等破坏概率则达到了5.12%;PGA0.1 g、烈度7度作用下，中等破坏概率达到了34.09%，轻微破坏概率则达到了55.72%，严重破坏概率达到了1.23%;PGA0.2 g、烈度8度作用下，中等破壞概率达到了87.33%，严重破坏概率达到了14.12%，轻微破坏概率达到了79.83%;PGA0.4 g、烈度9度作用下，完全破坏概率达到了14.44%，严重破坏概率达到了56.23%。2号墩在烈度6度作用下，轻微破坏概率为11.23%，中等破坏概率达到了4.23%;7度烈度下，中等破坏概率为28.35%，轻微破坏概率为48.81%;8度烈度下，轻微破坏概率87.72%，中等破坏概率73.23%，严重破坏概率11.22%;9度烈度下，完全破坏概率9.12%，严重破坏概率48.44%[4-6]。

横桥向地震动下，2号墩相对于1号墩的损伤程度较轻，均存在轻微破坏形式，严重破坏、中等破坏损伤概率差异性较小，完全破坏时1、2号墩的损伤概率差异性较大;地震动强度提升会导致1号墩更容易达到破坏状态;横桥向相对于纵桥向进行地震动输入时，2号墩相对于1号墩的损伤概率差值偏小;相较于横桥向，纵桥向1号桥墩比2号墩具备更为明显的损伤程度[4-6]。

4.3 纵横桥向地震响应对比

项目开展1、2号墩顺横桥向的易损曲线对比分析，可以发现，1、2号桥墩的横桥向地震动输入时的损伤概率都要小于纵桥向;在轻微及中等破坏状态下，横桥向桥墩损伤概率要小于纵桥向，在严重及完全破坏状态下，横桥向桥墩损伤概率要远小于纵桥向。经过相关原因分析，纵桥向具备较大水平刚度的桥面铺装，1、2号桥墩地震动作用下存在较为明显的耦合效应，1号桥墩相较于2号桥墩要矮得多，其具备较弱的地震动抵抗水平，为此，1号桥墩的损伤程度较大，尤其在严重及完全损伤状态下的桥墩力学响应更为明显[3]。

5 总结

城市曲线梁桥的应用数量越来越多，在地震频发区域，开展梁桥关键结构地震易损分析极其重要。该文采取OpenSees在充分考虑桩土效应及主梁边界约束的简化模型基础上对6跨双柱墩曲线连续梁桥1、2号桥墩地震动下的损伤概率进行比较分析，其中纵桥向损伤概率普遍要比横桥向要高，为此，设计中需要加强纵桥向桥墩的保护，且尽量采取曲率半径较大的设计思路避免桥墩损伤破坏。

参考文献

[1]台玉吉， 惠迎新， 师新虎，等. 轻骨料混凝土桥梁地震易损性分析[J]. 铁道科学与工程学报， 2020（1）： 10-11.

[2]张智， 李小军， 兰日清， 宋辰宁. 斜交连续刚构桥桥墩地震易损性分析[J]. 地震工程学报， 2020（6）： 49-59.

[3]Hwang H， Liu J B， Chiu Y H. Seis mic Fragility Analysis of Highway Bridges[C]//Referenz modellierung. 2001：1-34.

[4]刘小璐， 苏成. 大跨度桥梁地震易损性分析的时域显式法[J]. 振动工程学报， 2020（4）：9-12.

[5]郑见锋. 基于等效荷载位移曲线桥梁刚度性能研究[J]. 中国住宅设施， 2021（12）：3-5.

[6]沈惠军， 王浩， 郑文智，等. 多维地震作用下高铁桥梁圆端形桥墩易损性分析[J]. 地震研究， 2021（2）：81-83.