受约束混凝土的应力应变模型研究综述★
2022-04-14徐秀凤孔子昂王洪宝
徐秀凤,孔子昂,王洪宝
(1.青岛黄海学院建筑工程学院,山东 青岛 266427; 2.浙江绿城建筑设计有限公司青岛分公司,山东 青岛 266071)
1 概述
约束混凝土的单轴应力应变关系是预测梁、柱、剪力墙等结构构件承载力、变形能力和耗能能力等力学性能的基础。随着纤维模型等主要受材料单轴应力应变关系影响的数值分析模型的发展及性能化抗震设计方法的计算需要,对约束混凝土的本构要求越来越高,尤其是对构件进入软化阶段后的力学行为的预测越来越受到重视。
通过对素混凝土应力应变关系的研究,研究者们积累了丰富的应力应变模型,在这些模型的基础上结合试验研究,提出了很多适用于受约束混凝土的应力应变模型。早期的研究者们(1980年前)通过试验研究了影响应力应变模型的相关参数,随后建立了许多适用于普通混凝土的应力应变模型,随着高强混凝土的应用,在1990年以后掀起了对高强混凝土力学性能研究的高潮,提出了很多适用于高强混凝土的应力应变模型,并重点研究了构件在受力过程中箍筋应力的变化,少数研究者也做了将普通混凝土和高强混凝土应力应变模型进行统一的尝试,与此同时人们也逐渐认识到试验测量方法存在的缺陷可能导致应力应变模型的失真,提出了CDZ模型(Compressive Damage Zone Model)来描述应力应变曲线的软化段。2000年以后,依据充分的试验数据,很多研究者都提出了适用性较广的箍筋约束下的普通混凝土和高强混凝土单轴受压应力应变模型,同时这一时期,随着新的约束技术的发展,研究者把更多精力投入到钢管混凝土和FRP约束混凝土的研究中,并根据被动约束的特点,建立了横向应变与轴向应变和侧向混凝土应力状态之间的关系,从而提出适用于任何约束材料约束下的混凝土应力应变模型。
2 约束应力应变模型早期的发展(1980年前)
早在1903年,Considere[1]第一个指出了侧向约束作用可以提高混凝土构件轴向抗压强度。随后研究者们开展了一系列主动和被动围压下的混凝土试验,并提出了相应的模型,但这些模型大多采用小比例试验的结果,即采用边长或直径小于200 mm的构件的试验结果。同时,随着研究的深入,研究者们对约束混凝土破坏机理的加深,模型考虑的控制参数也在逐渐增多,模型也得到了逐步改进。1955年,Chan[2]将体积配箍率作为唯一影响参数,提出了三线性的应力应变关系。1964年,Roy和Sozen[3]通过小比例试验研究认为矩形箍筋并不能提高峰值承载力,并提出了包括体积配箍率和短边尺寸与箍筋间距之比的两参数双线性应力应变关系。1967年,Soliman和Yu[4]通过小比例偏心轴压试验,提出了由上升抛物线段、水平直线段和下降直线段组成的模型,模型中考虑了箍筋截面积、箍筋间距及截面长宽比等三个参数。1971年,Sargin[5]通过对小比例轴心受压和偏心受压试验的结果进行回归,给出了峰值应力应变的经验公式,同时采用一个解析式的形式表达了模型的上升段和下降段,模型中考虑了体积配箍率、箍筋间距与截面宽度之比、钢筋强度及混凝土强度等参数。同年,Kent和Park[6]根据研究并结合前人的试验结果提出了新的应力应变模型,模型中开始关注约束混凝土的残余应力(0.2fc),这一特征为很多研究者所接受,但由于研究基础的局限性,作者认为矩形箍筋对峰值应力的提高并没有作用。1977年,Vallenas等[7]在Kent-park的基础上对模型进行了修正,考虑了箍筋对峰值应力的提高作用,并考虑了众多参数对模型的影响,模型的参数包括体积配箍率、纵筋配筋率、箍筋和纵筋直径、箍筋间距与截面宽度之比、钢筋和混凝土强度等。
可以发现,在箍筋约束的混凝土应力应变模型早期的发展过程中,由于试验方法设备的限制,以及对约束混凝土破坏机理的认识不足,对影响参数的研究并不充分,提出的模型均存在一些缺陷,但随着研究的深入,提出的应力应变模型也得到了逐步完善。
3 约束应力应变模型1980年后的发展
1982年,Sheikh等[8]首次在模型中考虑了受约束纵筋的分布对约束效果的影响,并依据试验提出了一种全新的受矩形箍筋约束的混凝土的应力应变模型。作者通过箍筋在约束中的拱行为定义了有效约束面积,并将强度提高系数定义为有效约束面积、箍筋强度及体积配箍率的函数。通过24组正方形短柱轴心受压试验标定了分别控制约束平面内外有效约束面积大小的参数α,θ,以及由箍筋强度和体积配箍率共同决定的未知量β,γ。Sheikh等提出的曲线类型与试验曲线仍有较大差距,不能代表约束混凝土应力应变曲线的普遍特征,如文中对εs2的预测某些情况下误差可达40%以上。同时由于试验设备的测量范围的限制,所选取的试验未取得ε0.85(构件承载力下降到0.85倍峰值应力所对应的应变)后的试验数据,因此未能对约束混凝土全应力应变曲线做出有效估计,但对于有效约束面积的定义方法为许多研究者所采纳,对于推动进一步研究具有积极作用。随后Sheikh分别在1986年和1992年通过偏心加载的研究和不同轴压水平下的偏心加载的研究对1982年的模型进行了改进,以考虑应变梯度效应及轴压水平对应力应变模型的影响。
1988年,Mander等[9]提出了一种比之前所有模型适用范围都广的约束混凝土应力应变模型,模型中考虑了箍筋形式(螺旋箍、圆形与方形的普通箍筋)、截面形状(圆形、正方形、矩形面)、加载速率、加载模式(单调、循环加载)、纵筋的分布等影响因素,讨论了动力因素对于模型的影响,并通过能量守恒的方法计算了当第一根箍筋断裂时的混凝土压应变。在计算有效约束应力时,Mander基本沿用了Sheikh的方法,但Mander的模型基于Popovics提出的曲线,抓住了试验曲线的主要特征,更符合实际情况;Sheikh在标定峰值应力应变等关键参数时,完全采用了数据回归的方法,表现出明显的局限性;而Mander在计算峰值应力时采用了William-Warnke五参数破坏面,该准则已被验证具有很高的精度;在计算下降段控制参数εcu时,采用能量守恒的方法,即箍筋屈服的能量等于约束与未约束混凝土曲线之间的面积与纵筋屈服时能量之和,采用此方法得到的计算结果与试验结果非常吻合;峰值应变采用1928年Richat提出的经验公式,该公式也被广泛应用[10]。然而,Mander模型仍具有一定的局限性,如:动力影响系数基于的试验数据较少,适用程度仍需进一步验证;对于矩形截面,约束峰值应力需要查图,较为烦琐,对此,Saatcioglu[11],Cusson[12]和Paultre等[13]在此基础上均提出了简化的计算方法;模型只适用于普通箍筋和普通强度混凝土,且假设峰值应力时箍筋已经达到屈服,这已被证明存在高估试验曲线的风险;同时,在计算εcu时,Mander提出的单位体积钢筋的屈服耗能对于我国所采用的钢筋是否适用应做进一步的研究。
1992年,Saatcioglu和Razvi基于Hognestad[14]的模型提出了同时适用于轴心和偏心加载下普通强度混凝土的单轴受压应力应变模型,通过采用相同应变速率下的素混凝土参数以考虑应变速率的影响,该模型与Sheikh和Mander模型最大的不同在于,作者提出了等效均布侧向力的概念,而未采用通过考虑拱行为定义的有效约束系数,通过试验回归的方法标定了系数k2对平均侧向应力进行折减,从而得到等效均布侧向应力。1995年,Saatcioglu[15]通过一组试验进一步验证了轴心加载模型对偏心加载试验的适用性,结果表明通过轴心加载得到的应力应变模型同样适用于偏心加载试验,并指出是由于以往的模型不够精确导致了轴心模型应用于偏心加载试验时的失效。然而,由于基于试验的数据较少,对于应变速率的影响Saatcioglu模型可能考虑不足,同时由于基于Hognestad曲线,Saatcioglu模型在初始刚度上也存在一定误差。
研究者们在计算峰值状态下的有效侧向压力时,往往假设箍筋已经达到屈服。1992年,Madas和Elnashai[16]指出,箍筋约束属于被动约束,纵向峰值应变与箍筋屈服未必同时发生。因此,作者基于各向同性的三维模型,并通过泊松比的变化来考虑混凝土变形中的非线性,提出了一种伪三维模型,由于泊松比和轴向应变的相互影响,需要通过增量形式计算受约束的应力应变关系。分析指出,作者提出的应力应变模型具有同3D模型一样的精度,但计算时间与Mander模型相当,并且比Ahmad[17]模型具有更广的适用性。
1995年,Cusson和Paultre首次建议采用fle/fco作为有效约束指标,并将其作为模型和关键参数标定中的唯一指标,这一参数也为许多后续的研究者所采纳。同时,Cusson和Paultre在估计箍筋应力方面做了进一步的简化,Madas和Elnashai提出的箍筋应力计算方法的缺点在于需要增量计算,因此模型的表达形式是隐式的,不易于应用,因此作者提出只需要计算峰值应力下箍筋的应力,并假设在εcu时箍筋已经屈服,以此得到显式的应力应变关系。Cusson和Paultre提出的模型可以在素混凝土与约束混凝土之间互相转换,进一步提高了模型的适用范围。但该模型除了对峰值应力预测误差10%以内之外,对其他的参数的预测仍有改进空间,同时,迭代方法被证明当初始值与实际应力相差较远时将无法收敛[18]。
4 箍筋约束下高强混凝土的应力应变关系
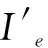
(1)
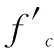
(2)
(3)
5 结语
本文介绍了箍筋约束普通混凝土和高强混凝土应力应变本构模型的发展历程,其中包括Sheikh模型、Mander模型、Hognestad模型、Paultre模型等典型的混凝土本构关系模型的性能特点和适用范围等,可为工程设计时的选用及相关研究工作提供参考。
