考虑初始缺陷的附着式升降脚手架稳定性分析

李鹏举，刘光明，徐 彬，王 琪，周 磊

(1.中铁城建集团第一工程有限公司，山西 太原 030024；2.山东大学，山东 济南 250100； 3.杭州市钱江新城投资集团有限公司，浙江 杭州 310000)

1 概述

强度问题、刚度问题和稳定性问题都是钢结构受力性能分析中很重要的部分[1]。本文主要分析钢结构的稳定性问题。在以往的研究中，何法伟等[2]以钢构件的振动频率值作为监控参数，分析了钢构件在失稳过程中轴向荷载同一阶振动频率的关系；刘霞等[3]基于ABAQUS有限元软件分析钢框架在失稳时内部能量的变化，从能量方面对钢框架倒塌进行了预测和分析；赵羿[4]针对于单层网壳钢结构冷却塔节点研发、节点抗弯性能及结构静力稳定性能开展研究，给出了考虑偏心受力作用的节点刚度半刚性钢冷塔稳定性分析的迭代方法。

上述研究对于钢构件失稳进行大量研究，但目前国内外学者对于考虑初始缺陷的附着式升降脚手架稳定性分析研究投入较少。由于附着式升降脚手架存在工作面离地面远且杆件多的特点，若在使用附着式升降脚手架时发生结构整体或局部失稳的情况，则会造成严重的工程事故。因此本文考虑初始几何缺陷、材料非线性的非线性稳定性分析，对附着式升降脚手架进行屈曲稳定分析，相关研究成果可为提高附着式升降脚手架的安全稳定性提供参考。

2 工程概况

本文基于济南市某超高层项目，本项目主要由1栋34层主塔楼及其6层裙房和2层整体地下车库组成，主塔楼建筑高度为165.5 m，结构类型为框架-核心筒，楼层边柱均为倾斜型钢混凝土柱，每根柱切斜角度不同。本工程34层主塔施工至第7层后考虑搭设附着式脚手架，直至主塔主体结构封顶后，完成爬架高空拆除。

3 特征值屈曲有限元分析

3.1 材料参数

所取附着式脚手架每榀外排高度20 m，内排高度18 m，架体宽度0.6 m，水平跨度为10 m。使用有限元软件ANSYS进行建模分析，模型整体采用Beam188单元进行模拟，采用理想刚接模拟螺栓连接[5]，架体构件材料均为Q235钢材，容许应力为205 MPa，材料参数见表1，架体材料截面尺寸见表2，有限元模型见图1。

表1 模型材料参数

表2 附着式升降脚手架构件尺寸表

3.2 计算工况和荷载选取

根据《建筑结构荷载规范》，不同工况下活载取值如表3所示。

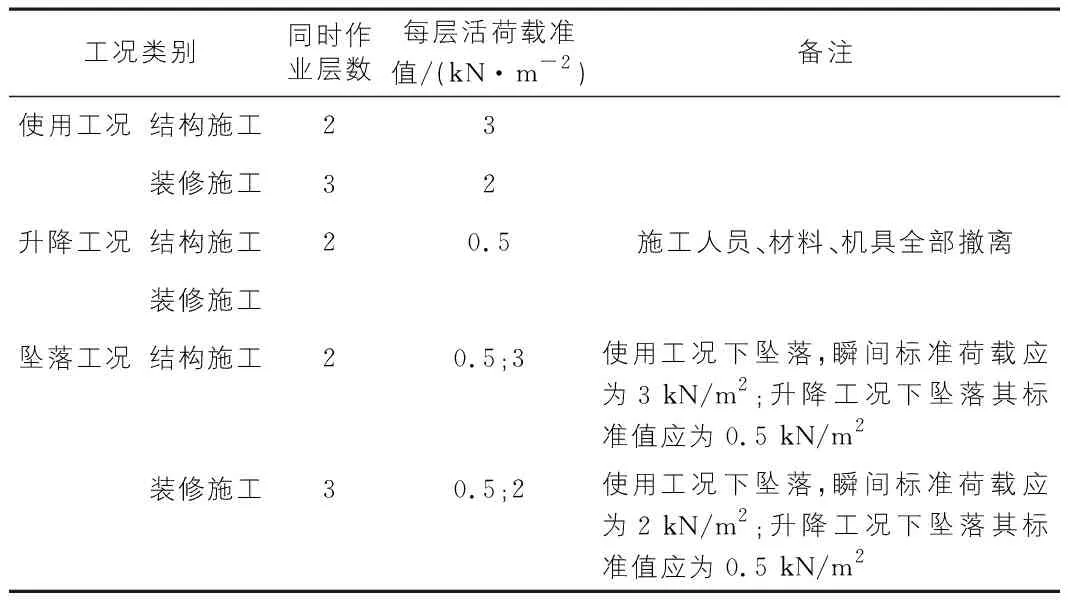
表3 施工活荷载标准值

本工程只有在主体结构施工过程中去使用脚手架。另外，由于顶上两层脚手板是人员施工主要活动的地点且施工器械材料也大量堆积在此，因此选取顶上两层脚手架进行活载施加。按照以下两种荷载效应组合进行分析：1)恒载+施工活载；2)永久荷载+0.9(施工荷载值+风荷载)。

3.3 分析结果表

虽第1阶失稳模态为最容易发生失稳的形式，但因其对应的屈曲荷载较大，实际情况中产生第1阶失稳模态的可能性较低，因此本文特征值屈曲分析中，主要考虑4阶屈曲模态和屈曲系数。

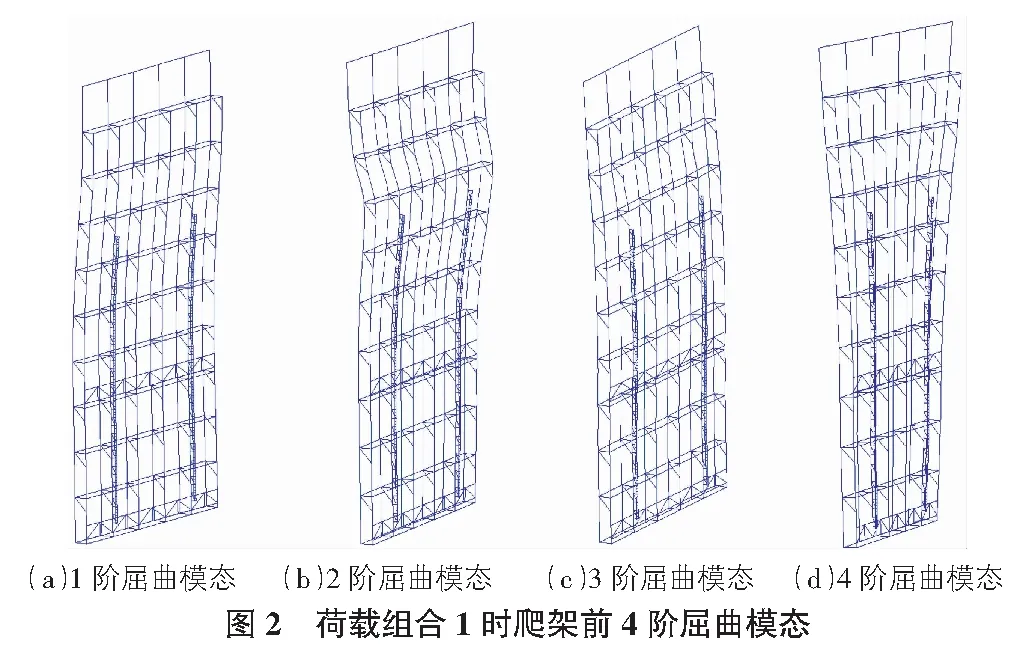
1)荷载组合1：恒载+活载(见表4，图2)。

表4 荷载组合1时附着式脚手架屈曲分析结果

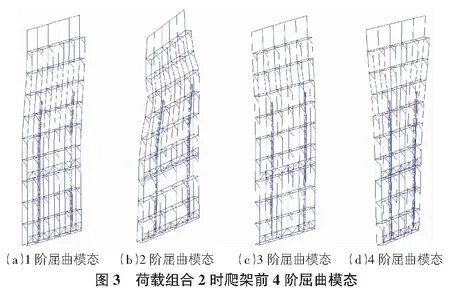
2)荷载组合2：恒载+0.9(活载+风载)(如表5，图3所示)。

表5 荷载组合2时附着式脚手架屈曲分析结果

从表4和表5中看出，荷载组合1中1阶屈曲安全系数是15.774；荷载组合2中1阶屈曲安全系数是16.586，数值均大于1。这说明爬架提升时抗失稳性能较好，抗失稳性能满足实际工程中屈曲系数大于3的实际需求[6]。

由图2，图3对比观察到，爬架的前4阶屈曲模态基本一致。在荷载组合2效应作用下的前4阶的屈曲安全系数比在荷载组合1作用下的值都要大。两个荷载组合的差别主要在于荷载组合1没有考虑风荷载，而荷载组合2考虑到了风荷载，这说明在不考虑风荷载的作用下爬架屈曲更容易发生。爬架提升作业在风速大于5级时禁止进行可能为产生上述现象的原因，因此本文在分析屈曲模态时考虑较小的风荷载。

4 非线性稳定性有限元分析

在实际安装和使用过程中，爬架结构的初始缺陷是无法避免的，爬架结构材料的非线性行为也是客观存在的[7-9]。本节在特征值屈曲分析研究的基础上，考虑初始缺陷和材料非线性行为，对爬架进行非线性稳定性有限元分析[10]，提高爬架稳定性的计算精确性。采用弧长法[11]对结构几何非线性问题进行跟踪求解，并采用BKIN模型描述爬架的非线性行为。表6为根据相关文献[12-13]及现场查看总结的附着式脚手架初始缺陷统计表。

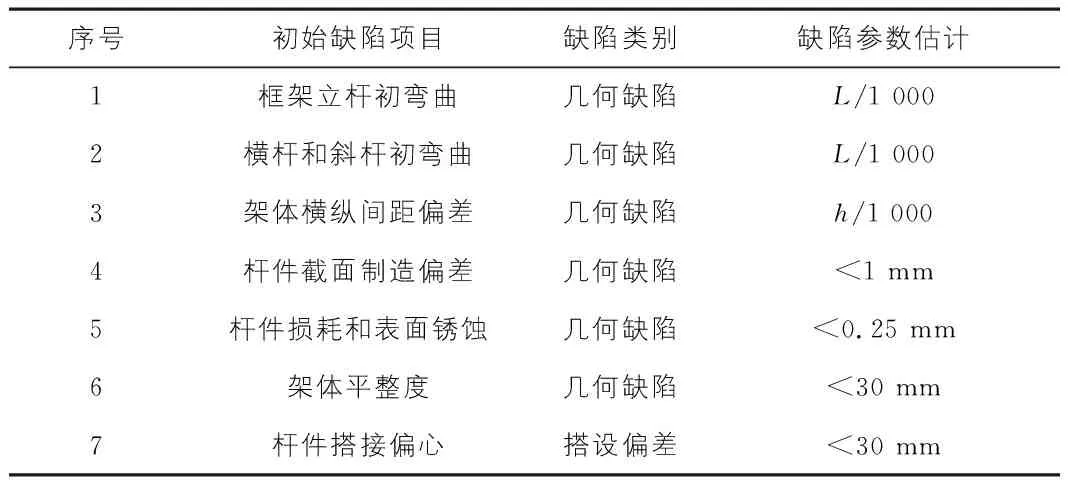
表6 附着式升降脚手架初始缺陷统计

4.1 模型加载

在ANSYS特征值屈曲分析中求得的屈曲系数是全荷载作用的缩放系数，由此得出式(1)。

结构屈曲荷载=屈曲系数×(恒载+活载)

(1)

由于式(1)不符合工程的实际情况，因此编写迭代计算APDL语言(见图4)，对所选荷载工况进行迭代求解至1阶屈曲系数输出结果为1，由此得出式(2)。

屈曲荷载=1.0×(恒载+活载系数×活载)

(2)

由式(1)与式(2)的对比观察到，式(2)符合工程实际。在荷载组合1作用下输出的1阶特征值屈曲活载屈曲系数为38.24，之后再乘以1.2的载荷系数。得到的值作为非线性稳定分析的初始活载并将其施加于架体，加载过程采用弧长法。

4.2 分析结果

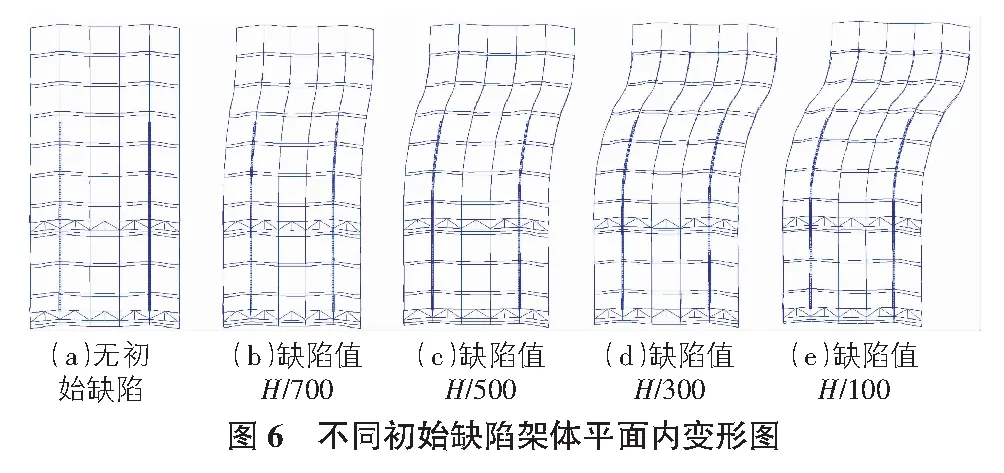
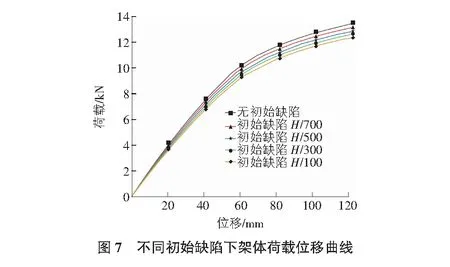
考虑初始几何缺陷的爬架变形有限元计算结果如图5，图6所示，不同初始几何缺陷数值下节点荷载位移曲线如图7所示，相应的极限承载能力和稳定系数见表7，表8。

根据以上分析结果可得出以下结论：

1)由表7可以看出，随着初始几何缺陷的增大，架体的极限承载能力逐渐降低，由13.1 kN下降至12 kN，仅仅下降了8.4%。这说明初始几何缺陷的变化对附着式升降脚手架极限承载能力的影响小。

2)由图5，图6可以看出，从无初始缺陷到缺陷值逐渐增大的过程中，架体平面内刚度和平面内扭转刚度不断降低，架体变形幅度不断增长，且变化幅度均十分明显。架体的失稳模态包括平面外弯曲失稳、平面内弯曲失稳和沿中线扭转失稳三种。这说明在考虑初始几何缺陷后架体的失稳模态变化较大。

3)由表8可以看出，从无初始缺陷到缺陷值逐渐增大的过程中，特征值屈曲分析整体稳定系数基本不发生变化，基本一直保持在38.24左右；从无初始缺陷到缺陷值逐渐增大的过程中，非线性稳定性分析整体稳定系数从14.56下降至13.33。这说明特征值屈曲分析整体稳定性系数偏不保守且基本不随缺陷值的改变发生变化。

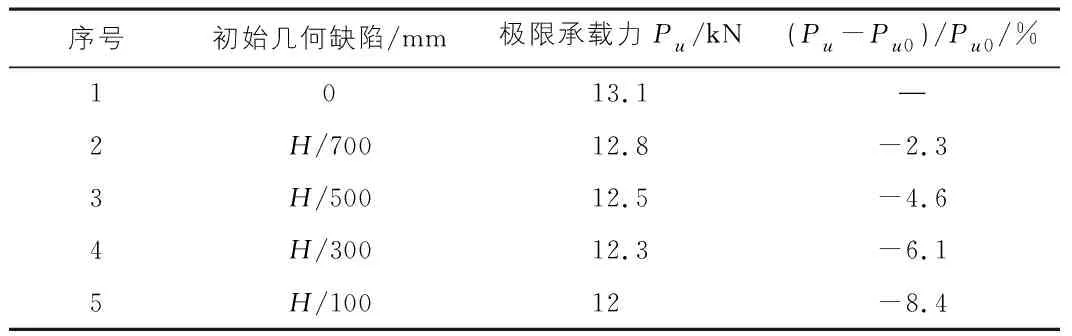
表7 非线性分析极限荷载统计表

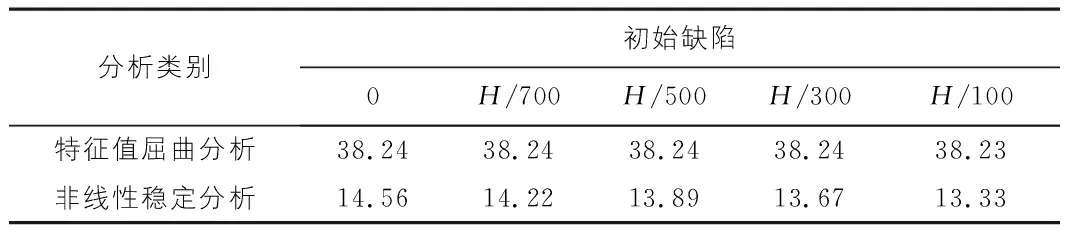
表8 爬架整体稳定系数统计表

5 结语

本文通过建模分析可以看到，特征值屈曲分析整体稳定性系数偏不保守且基本不随缺陷值的改变发生变化，不可以用于实际工程；在结构非线性行为中，从无初始缺陷到缺陷值逐渐增大的过程中，整体稳定系数下降明显，爬架失稳模态更复杂，且较特征值屈曲分析下的整体稳定系数下降程度大，实际工程用此方法进行爬架稳定分析更为准确合理。