基于参数优化VMD和样本熵的滚动轴承故障诊断

刘建昌 权贺 于霞 何侃 李镇华

滚动轴承是旋转机械设备的关键零件,及时、正确地诊断滚动轴承的状态对整个设备来说至关重要.滚动轴承故障诊断的流程分为3 部分:信号处理、特征提取和诊断识别.由于设备运行环境噪声的干扰,通过传感器获得的信号包含大量冗余信号,这就需要借助信号处理技术去除嘈杂的冗余信号,提取出故障特征.故信号处理和特征提取部分是整个诊断流程的关键.

Liu等[1]利用经验模态分解 (Empirical mode decomposition,EMD)和相应的 Hilbert 谱进行齿轮箱故障诊断,与连续小波变换相比诊断正确率有明显提升;程军圣等[2]提出了一种基于内禀模态(Intrinsic mode function,IMF)奇异值分解和支持向量机 (Support vector machine,SVM)的故障诊断方法,采用 EMD 方法对振动信号进行分解,得到若干个内禀模态分量形成特征向量矩阵,对该矩阵进行奇异值分解,提取其奇异值作为故障特征向量,并根据 SVM 分类器的输出结果来判断故障类型.针对 EMD 方法存在过包络、欠包络、模态混淆和端点效应等问题,Smith[3]于 2005 年提出了一种新的自适应信号分解方法 ——局部均值分解 (Local mean decomposition,LMD)方法.Li等[4]研究了LMD 方法,并在电机轴承故障诊断中进行了试验.LMD 方法避免了过包络问题,减小了模态混淆和端点效应,但是与 EMD 一样,两者都属于递归模式分解,误差会在分解过程逐渐积累,后续很多学者都在其基础上作了改进,但无法从根本上解决模态混淆和端点效应问题[5-7].Dragomiretskiy等[8]于2014 年提出一种新型的可变尺度的处理方法 ——变分模态分解 (Variational mode decomposition,VMD)方法.与 EMD和 LMD 方法的递归模式不同,作为新型的自适应信号处理方法,VMD 方法引入变分模型,将信号的分解转换为约束模型最优解的寻优问题,可以避免端点效应、抑制模态混淆,并且具有很高的分解效率.

样本熵是 Richman等[9]于2000 年提出的一种度量时间序列复杂度的方法,与近似熵物理意义类似,都是衡量当维数变化时时间序列所产生的新模式概率的大小.评判原则为:时间序列越复杂,产生新模式的概率就越大,对应的熵值也越大;相反,若时间序列自我相似性越高,则样本熵值越小.由于啮合尺度的变化,滚动轴承在发生故障时振动状态会发生变化,即产生新的调幅-调频信号,故可以借助样本熵计算该状态下滚动轴承的信号复杂度,赵志宏等[10]也将样本熵运用在机械故障诊断上,取得了较好的效果;Marwaha等[11]借助样本熵量化心脏变异性时间序列的复杂度时,发现样本熵的评判结果与实际不符,并根据心脏跳动序列特点提出改进的样本熵,改 进后的样本熵评判结果较为合理.此外,谱峭度指标、能量熵和稀疏残差距离等作为故障特征在故障诊断中应用也较为广泛[12-13].

在信号处理和构建特征向量的基础上,合适的选择诊断方法也尤为重要.人工神经网络具有很强的自组织、自学习能力,在滚动轴承的故障诊断中应用较多[14-15].但构建合适的神经网络模型需要大量的故障样本数据,这也限制了人工神经网络在滚动轴承故障诊断领域的发展.SVM 是 Vapnik[16]在统计学习理论基础上提出的一种通用学习方法.作为经典的分类算法,SVM 在解决小样本和非线性问题中有独特的优势,已经广泛应用于故障诊断和模式识别等众多领域[17-19].在非线性问题上,SVM引入惩罚参数和核函数将其转化为高维空间的线性问题,进而实现有效分类,但选择不同的惩罚参数和核函数,SVM 的分类精度也相差较大,目前较多学者采用智能优化算法进行多核支持向量机研究[20-22].Tipping[23]于 2001 年提出的相关向量机 (Relevance vector machine,RVM)是基于贝叶斯框架的机器学习算法.较 SVM 而言,具有参数设置更为简单、稀疏度更高、基函数不受 Mercer 条件限制等优点,高明哲等[24]也在 RVM 的基础上提出基于多核多分类相关向量机 (Multi-kernel learning multiclass relevance vector machine,MKL-mRVM)的模拟电路故障诊断方法.Breiman[25]于 2001 年提出随机森林算法 (Random forest,RF),该算法是基于决策树的一种组合分类器.RF 通过 Bootsrap重抽样方法抽取样本,对每个样本进行决策树建模,最终通过多棵决策树的预测,并采用投票机制得到预测结果,弥补了 SVM 处理大样本数据时能力不足的缺点,目前在生物、故障诊断和临床医学等领域广泛应用.Waljee等[26]使用逻辑回归和 RF 建立预测模型,该模型大大提高了预测炎症性肠病(Inflammatory bowel disease,IBD)相关住院和使用门诊类固醇的能力,可用于区分高风险和低风险疾病发作的患者,实现个性化治疗.同样在 IBD 疾病领域,Waljee等[27]借助 RF 建立预测模型,实现在临床护理中识别使用硫嘌呤的 IBD 患者,可以预测客观缓解率.张西宁等[28]利用多维缩放法对滚动轴承的故障特征集进行降维,采用随机森林对降维后的故障特征进行诊断识别,较使用原始特征集的随机森林平均准确率有明显提高.本文以滚动轴承为背景,样本数据较小,故选择经典的 SVM 分类器作为诊断方法.

针对滚动轴承故障特征提取不丰富而导致诊断识别率低的情况,本文提出基于参数优化VMD和样本熵的特征提取方法,参数优化的 VMD 方法分解原始振动信号得到本征模态分量 (Intrinsic mode function,IMF),提取各 IMF 分量的样本熵可以反映振动信号丰富的故障特征,并采用 SVM 进行故障识别.VMD 方法的分解效果受限于惩罚因子和分解个数的选择,本文分析了这两个影响参数选取的不规律性,采用遗传变异粒子群算法进行参数优化,利用参数优化的 VMD 方法分解振动信号.样本熵在衡量滚动轴承振动信号的复杂度时具有一定的局限性,即熵值的大小并不总是与信号的复杂度相关.本文分析了滚动轴承的故障机理,提出基于滚动轴承故障机理的样本熵算法,此样本熵算法衡量振动信号的复杂度与机理分析的结果一致.仿真实验表明,基于参数优化VMD和样本熵的特征提取方法可以提高滚动轴承故障诊断的准确率.

本文结构安排如下:第 1 节介绍 VMD 方法的分解原理,分析参数设置对其分解效果的影响;第2 节采用遗传变异粒子群算法进行参数优化,获取最优参数组合;第 3 节分析样本熵在衡量滚动轴承振动信号复杂度时的局限性,提出基于滚动轴承故障机理的样本熵算法;第 4 节阐述基于参数优化VMD和样本熵的滚动轴承故障诊断步骤,并在第5 节进行仿真实验;第 6 节对全文进行总结.

1 变分模态分解原理及参数设置

VMD 方法分解过程实质上是一个变分问题的构造和求解过程,本节从构造和求解两方面介绍VMD 方法,引出 VMD 方法参数设置对其分解效果的影响.

VMD 方法定义了分解后的 IMF 分量为调幅-调频 (Amplitude modulation-Frequency modulation,AM-FM)信号,假定原始信号可以分解为K个IMF 分量,则第k个IMF 分量的表达式为

式中,Δf表示瞬时频率与中心的最大偏差,fFM表示瞬时频率的偏移率,fAM表示包络函数Ak(t)的最高频率.在各分量之和等于输入信号的约束条件下,使得各分量的估计带宽之和最小,再经过一系列变换,构造出如下的约束变分模型:

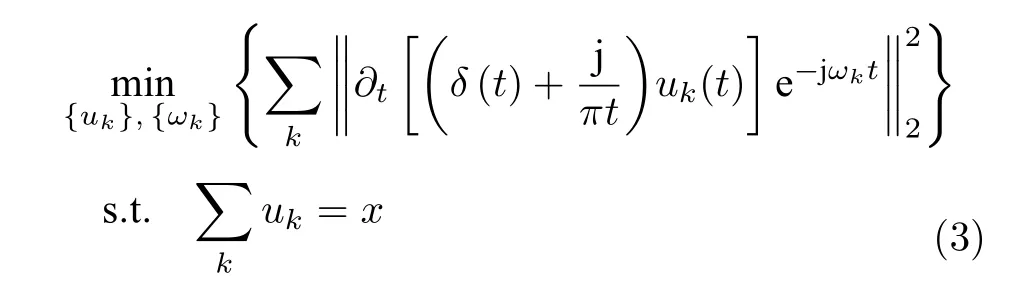
式中,{uk}表示分解得到的 IMF 分量;{ωk}表示 IMF 分量对应的中心频率;表示借助 Hilbert 变换得到 IMF 分量uk(t)的单边频谱;x表示原始的输入信号;表示 IMF 分量的总和.VMD 方法就是通过搜寻上述约束变分模型的最优解来自适应分解信号,在迭代求解时逐步更新每个分量的中心频率和带宽,最终根据信号自身的频域特性自适应划分出 IMF 分量.然而,在求解该模型时需要引入二次惩罚因子α和拉格朗日算子λ(t),将上述约束变分问题转换为如下的非约束变分问题:

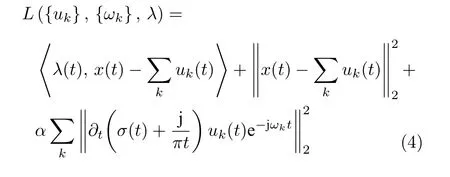
1.1 求解变分问题

引入乘法算子交替方向法 (Alternate direction method of multipliers,ADMM)解决上述非约束变分问题,主要思路是通过交替更新来寻找扩展 Lagrange 表达式的 “鞍点”,其中,n表示求解时的迭代收敛次数.

将式(6)中第1 项中的变量ω替换为ω-ωk,得到

将式(7)转换为非负频率区间积分的形式为

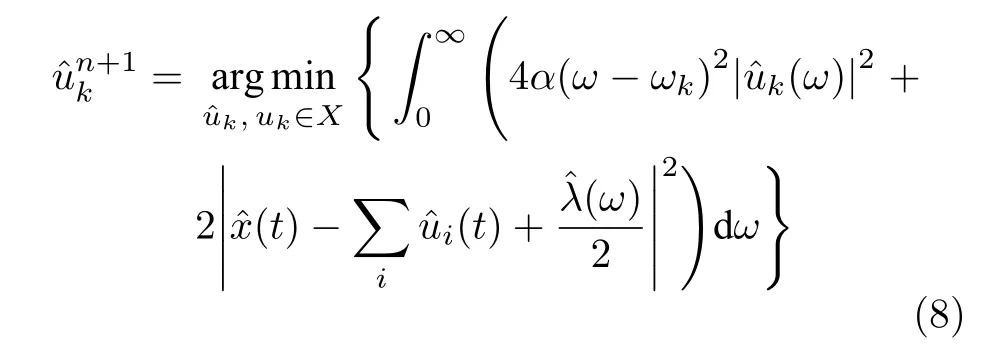
求解式(8),可以得到该优化问题的最优解为

1.2 变分模态分解方法的参数设置对其分解效果的影响

当滚动轴承的部件出现裂纹或者其他故障时,滚动轴承的啮合尺度会发生变化,进而轴承的振动状态会发生改变,由加速度传感器测得的振动信号中会含有大量的调幅-调频信号.为了准确地分析振动信号蕴含的特征信息,本文以调幅-调频信号作为仿真信号进行仿真实验,测试变分模态分解参数对分解效果的影响,该仿真信号为

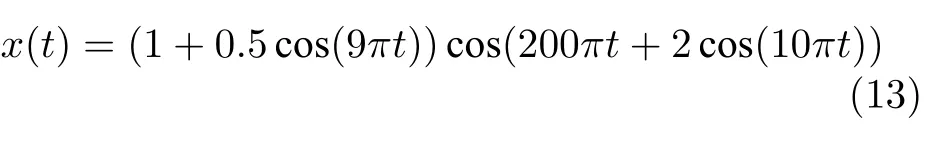
当采样频率fs为1 000 Hz 时,仿真信号的频谱如图1 所示,图中A表示仿真信号的幅值,f表示信号的中心频率.

图1 仿真信号的频谱Fig.1 The frequency spectrum of simulated signal

由图1 可以看出,该仿真信号主要包含 5 个频率成分:90 Hz,95 Hz,100 Hz,105 Hz和 110 Hz.VMD 方法在分解信号时,通过迭代搜寻变分模型最优解来确定各分量的频率中心及带宽,进而自适应地实现信号的频域剖分及各分量的有效分离.根据文献[8],VMD 算法需要确定的参数为:IMF 分量的个数K,惩罚因子a,凸函数优化相关参数tau,中心频率初始化设置init,中心频率更新时的相关参数DC,终止条件ε.K和a之外的参数对分解效果影响较小,设置为经验值,即tau=0,init=1,DC=0,ε=10-7.本文分析K和a对分解效果的具体影响如下.

1)K对分解效果的影响

选取α=2 000,K分别为 3,4,5,6 或 7时,借助 VMD 方法分解仿真信号,分解完成的中心频率变化曲线如图2 所示,图中n表示分解过程的迭代次数,f表示分量的中心频率.

由图2 可以看出,K分别为 3,4 或 5 时,分解出的信号频率个数逐渐增加,但均没有完全分解出信号包含的主要频率信号,即欠分解状态;当K=6 时,VMD 方法可以分解出原信号包含的频率信号;当K=7 时,在 95 Hz 附近,分解过程产生了虚假分量,即出现了过分解现象,且没有分解出 100 Hz 频率信号.可见,当K选择合适时,VMD方法可以很好地分解出原信号包含的频率成分,但是选择不合适则会产生欠分解和过分解现象.

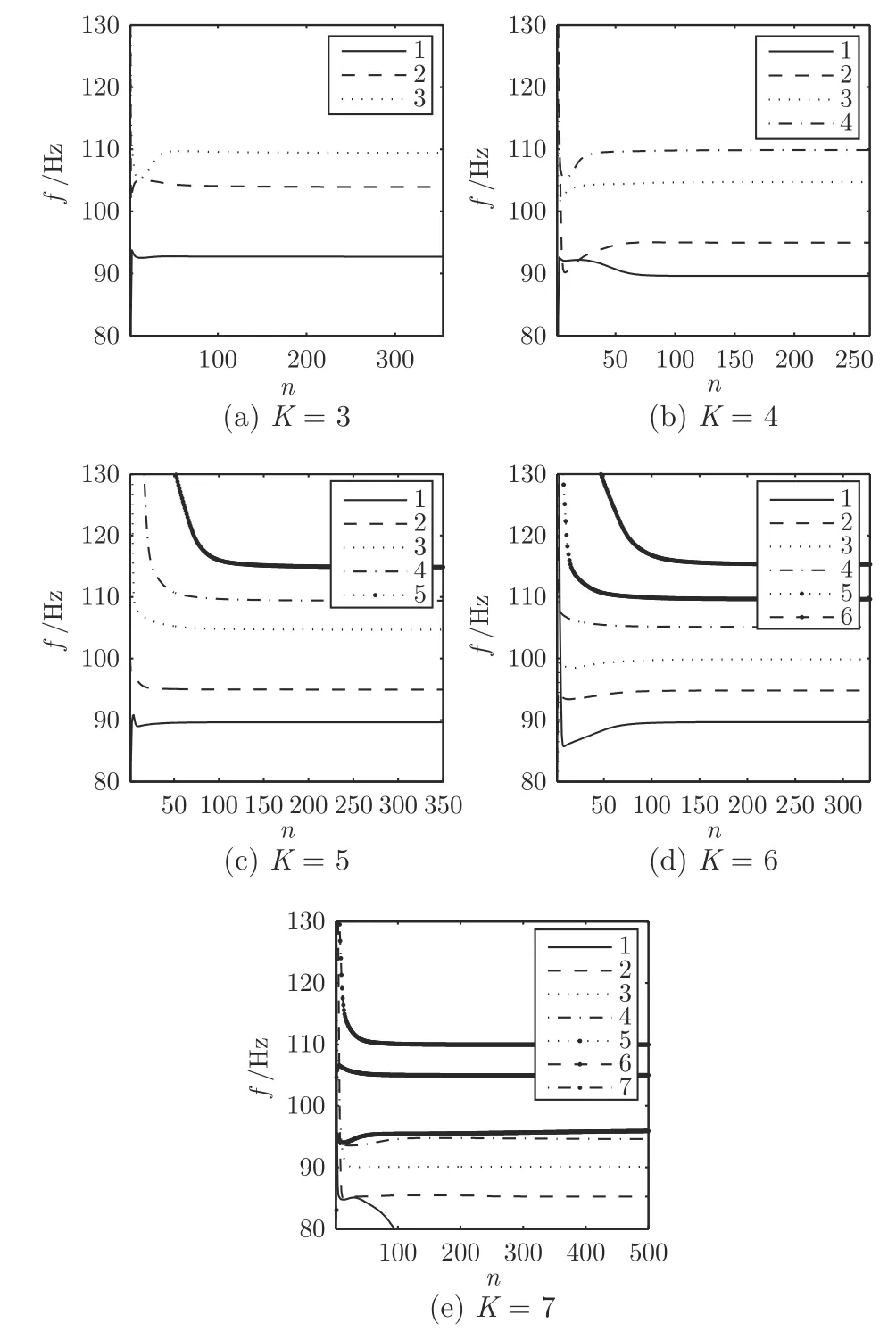
图2 中心频率随分解个数K的变化Fig.2 Evolution of central frequency with the number of decompositionK

2)α对分解效果的影响

选取K=6,α=0.3fs,0.6fs,fs,2.5fs,4fs和5fs.分解完成的中心频率变化曲线如图3 所示,图中n表示分解过程的迭代次数,f表示分量的中心频率.

由图3 可以看出,当α过小,即α=0.3fs时,100 Hz 的频率信号没有分解出来,是欠分解状态;当α=0.6fs时,在迭代初期,分解分量的中心频率出现混叠现象,迭代完成时 VMD 方法未能正确分解出原信号包含的频率信号;当α=fs时,在迭代后期,各分量中心频率能够很好地反映原信号包含的频率信号,但是分解完成的迭代次数较大;当α分别为 2.5fs,4fs或5fs时,在迭代后期,各分量中心频率可以反映原信号包含的频率信号,但达到最优效果的迭代次数减小后又增大,即 VMD 方法分解效率增高后又降低;同时当α= 5fs时,在迭代前期,110 Hz 频率附近产生了较长时间的混叠现象.可见,当K固定时,α的最优选择呈现出不规律性.

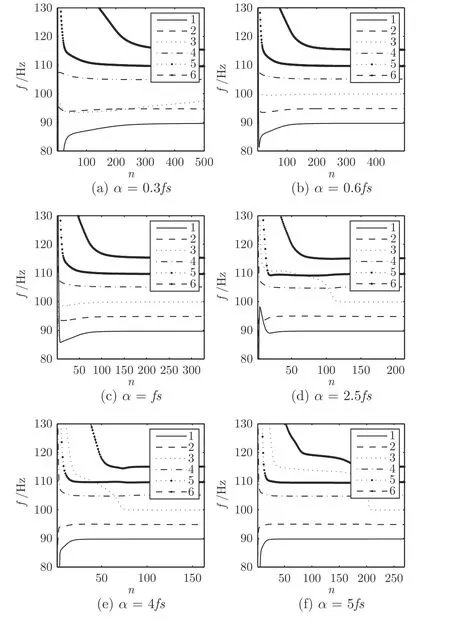
图3 中心频率随惩罚因子α的变化Fig.3 Evolution of central frequency with punishment factorα

综上分析可知,α和K的选择会影响 VMD方法的分解效果,且参数的选择是不规律的,即上述的分析方法只能得到相对最优的参数组合.为了选定最优的参数组合,使 VMD 方法可以提取出信号中丰富的特征信息,本文采用遗传变异粒子群算法进行参数优化.

2 基于遗传变异粒子群算法的参数优化

上一节分析了α和K的选择会影响 VMD方法的分解效果,且参数的选择是不规律的,即定参的设置方法不能得到最优的参数组合,故本节采用遗传变异粒子群算法进行参数优化,获取最优的参数组合.

粒子群算法是 Eberh等[30]于1995 年提出的一种全局优化算法,该方法是一种群智能优化算法,具有参数较少、容易调整的优点,同时也容易陷入局部最优,无法获取全局最优近似解,故本文在粒子群算法中引入遗传算法变异的思想,构造遗传变异粒子群算法.

定义遗传变异粒子群算法如下:在一个D维的搜索空间内,标记种群为X,种群X由m′个粒子组成,即X=[x1,x2,···,xm′],每个粒子在搜索空间的位置可以用D维向量表示,即xi=[xi1,xi2,···,xiD],D是待优化参数的个数;第i个粒子的移动速度vi=[vi1,vi2,···,viD],粒子的局部极值pi=[pi1,pi2,···,piD],该代种群的全局极值G1=[g1,g2,···,gD],次全局最优值个体最大最优保持代数为 maxAge,变异概率为q.为了防止粒子陷入局部最优,需要记录迭代过程中粒子个体最优的保持代数,当个体最优保持代数没有达到 maxAge时,每个粒子通过个体局部极值和全局极值来更新下一代的位置和速度,更新式为

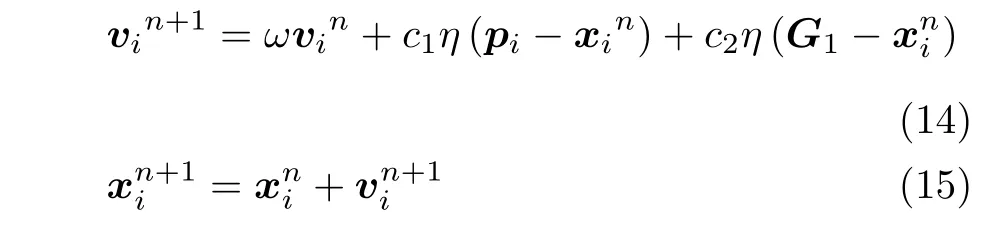
式中,ω为惯性权重,η为[0,1]之间的随机数,c1和c2为学习因子,分别代表了局部搜索能力和全局搜索能力,迭代次数n与上文定义一致,vi,pi,G1,xi均为D维向量.当前迭代次数的惯性权重ω的确定采用 Shi[31]提出的线性递减权值方法,计算式为

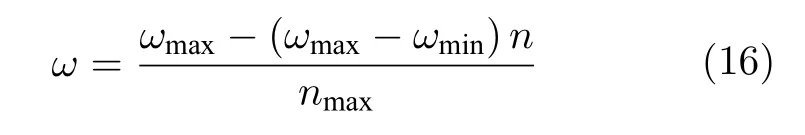
式中,ωmax和ωmin分别为最大最小惯性权重,n为当前迭代次数,nmax为定义的最大迭代次数.当个体最优保持代数达到maxAge,采用遗传变异操作更新粒子位置和速度使其跳出局部最优.

遗传变异粒子群算法适应度函数的选择如下:在参数优化时,VMD 方法分解效果的评判标准选用唐贵基等[32]提出的包络熵Ep概念,长度为N的时间信号x(j)的包络熵定义为

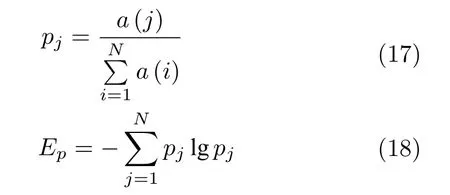
式中,i,j=1,2,···,N,a(j)是x(j)在 Hilbert解调后得到的包络信号,pj是对a(j)归一化后的结果,归一化既避免了 IMF 分量不同包络幅值的影响,也减小了微弱噪声的干扰,Ep是依据信息熵计算规则得到,本文依据Ep衡量 VMD 的分解效果.

滚动轴承的故障信号经过 VMD 方法分解后,若得到分量中包含的噪声较多,则会掩盖故障冲击特征,分量信号的稀疏性较弱,包络熵较大;相反,若分量中出现规律性的冲击脉冲,信号将会呈现较强的稀疏性,此时计算的包络熵较小.故在一组参数组合α和K的影响下,选择K个分量中最小的包络熵Ep作为局部极小熵 minEp,与该最小熵值对应的分量蕴含着丰富的特征信息.将局部极小熵值作为整个搜索过程适应度函数的一部分,寻找全局最佳分量对应的参数组合 [K0,α0].通过上述对参数α的分析,合适地选择α会降低 VMD的迭代次数,即 VMD 方法分解效率更高.故需要在分解效果最优时,尽可能达到较高的分解效率,本文在 minEp的基础上,加入迭代次数iter,构建适应度函数为

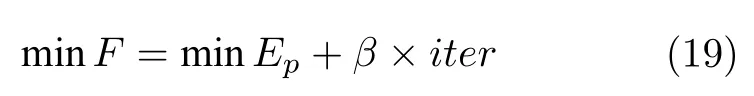
式中,β是适应度函数的量化因子,选取美国凯斯西储大学(Case Western Reserve University)电气工程实验室的轴承振动数据,滚动轴承的型号为SKF6205,损伤直径为 0.1778 mm,选取0 kW负载下转速为 1797r/min,采样频率为 12 kHz 时内圈故障数据,借助该数据分析 IMF 分量的Ep时,Ep在[4,5]区间内;在第1节参数分析时发现,参数设置不合适时,iter可能会达到限值 500 次,故需要对两者的量级预处理,β≈1/100.参数优化的目标是在分解效果最优时,尽可能满足较好的分解效率,即β≤1/100.以β的分母逐次增加 100 的规律观察 minEp和iter的变化,其中每个β值迭代 4 次,记录其中最小的值.当β减小至 1/1000时,minEp最小且iter较小,适应度函数更稳定,当继续减小β时可忽略iter对适应度函数的影响,也会出现 minEp较小的情况,故β的选择较为灵活,本文选用β=1/1 000.基于遗传变异粒子群算法的参数寻优流程如图4 所示.

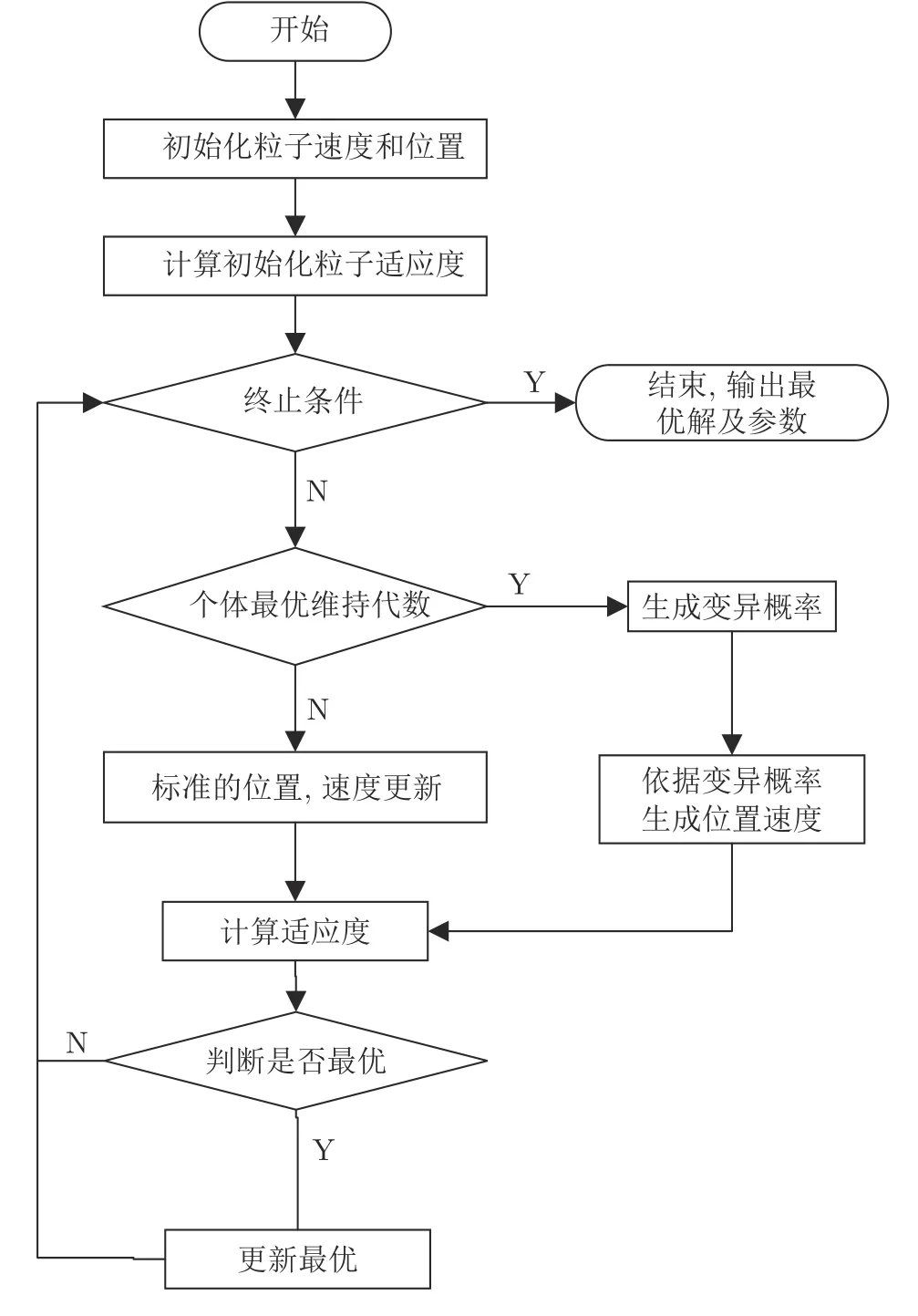
图4 基于遗传变异粒子群算法的参数优化流程Fig.4 Parameter optimization process based on genetic mulation particle swarm optimization

3 基于滚动轴承故障机理的样本熵算法

与近似熵相比,样本熵对数据长度的依赖性减小,抗干扰能力增强,已经广泛应用于脑电波信号和振动信号等研究中.计算样本熵需要确定两个参数,模板匹配长度m和阈值r,在文献[33]中,阈值r设定为时间序列标准差的 0.1～0.2 倍,m通常设为 1 或 2.

本文在借助样本熵衡量滚动轴承运行状态下振动信号的复杂度时,发现样本熵赋予正常信号更大的熵值,相反,故障状态的熵值更小.分析滚动轴承的故障机理,轴承部件产生裂纹或者其他损伤时,轴承的啮合尺度会发生变化,运行状态会发生改变,振动幅值会加剧,损伤部位变化的啮合尺度会使该处的振动幅值异常增大,反映在振动信号的波形中为周期性的冲击幅值.为了更加清晰地观察滚动轴承故障发生时的振动状态,本文选取美国凯斯西储大学电气工程实验室的轴承振动数据,滚动轴承的型号为 SKF6205,损伤直径为 0.1778 mm,选取 0 kW负载下转速为 1797 r/min,采样频率为 12 kHz 时内圈故障、滚动体故障、外圈故障和正常状态下的振动信号,4 种状态的振动信号如图5 所示.

由图5 可以看出,滚动轴承在正常状态时振动信号的幅值大部分在 [-0.2,0.2]区间内,振动信号的波动较小,运行状态较为稳定;滚动轴承在故障状态时振动信号的幅值大幅增加,即故障损伤导致啮合尺度变化,加剧了振动信号的波动.以外圈故障时的振动信号为例,振动信号的幅值在 [-5,5]区间内,且有周期性的冲击幅值,动态特性复杂.故结合4 种状态下的振动信号分析正常状态下振动信号的复杂度低于故障状态下的复杂度.在借助样本熵衡量滚动轴承在4 种状态下的振动信号的复杂度时,4 种状态下振动信号的样本熵为:正常状态时熵值为 0.9717,内圈故障时熵值为 1.5976,滚动体故障时熵值为 1.6937,外圈故障时熵值为 0.7099.正常状态下振动信号的样本熵值大于外圈故障时的样本熵值,依据样本熵的计算规则,时间序列越复杂,熵值越大,即正常状态下滚动轴承振动信号的复杂度大于外圈故障振动信号的复杂度,这与机理分析得出的复杂度不一致.导致样本熵值与振动信号的复杂度不一致的原因可能是阈值r的设置.在计算样本熵时,阈值r为原始振动信号标准差的 0.1～0.2 倍,由于故障状态下振动信号有周期性冲击幅值,该冲击幅值使阈值r变大,则模式匹配时的相似容限变大,模式匹配值变大,计算得出的熵值变小,即故障状态下振动信号的复杂度低.这种异常增大的阈值r忽略了周期性冲击幅值区间内振动信号的波动.为了验证阈值r的设置是由冲击幅值的影响,本文采用依拉达准则剔除部分冲击幅值,计算的样本熵值如表1 所示,表1 中熵值 1和熵值2 分别代表原始序列的样本熵值和剔除部分冲击幅值后的样本熵值.

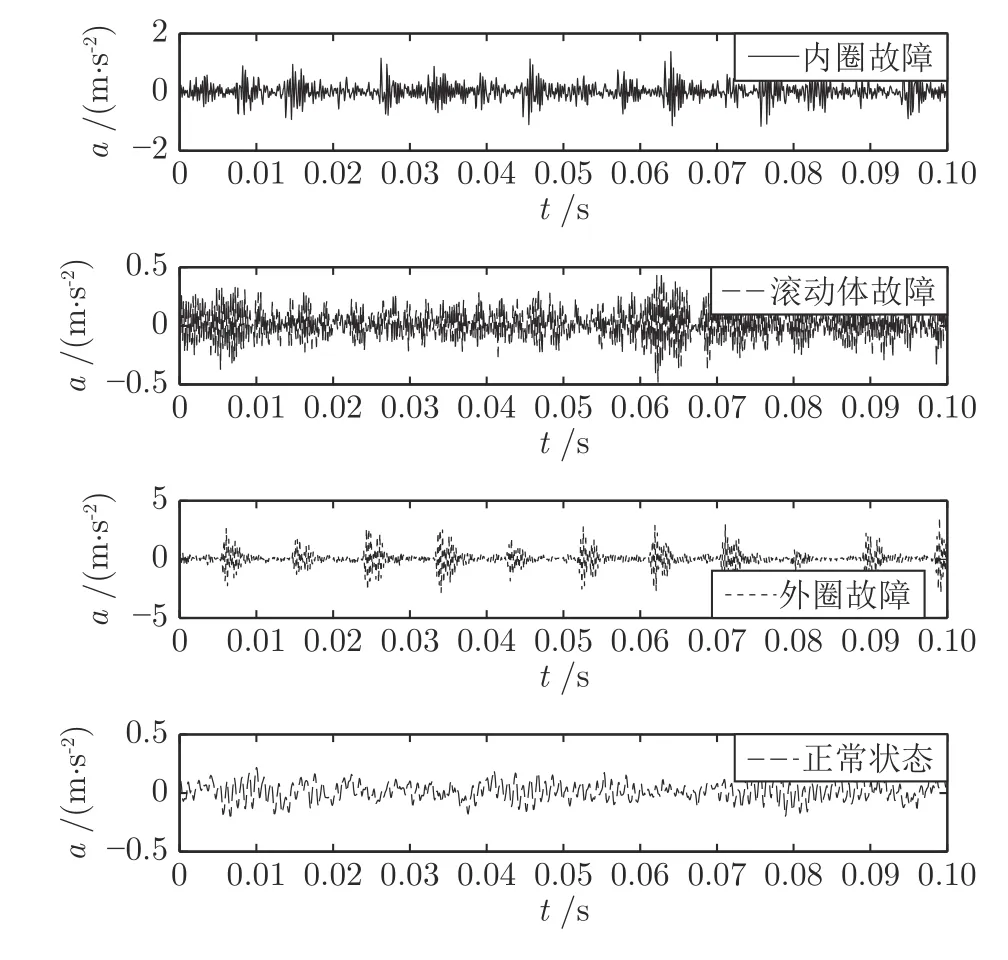
图5 4 种状态的振动信号Fig.5 Vibration signal in four conditions

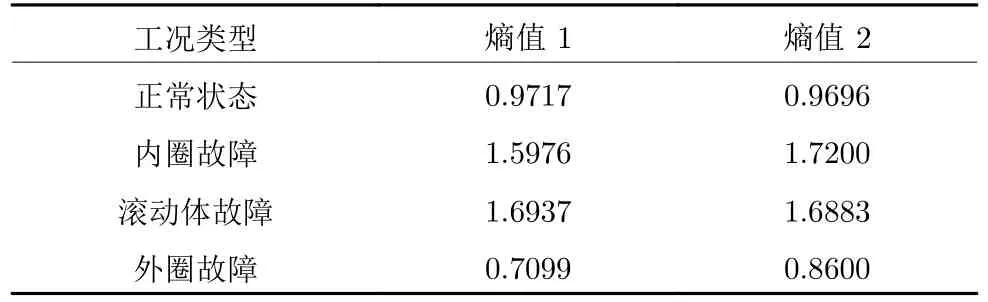
表1 样本熵值Table 1 Sample entropy

由表1 可知,在剔除部分冲击幅值后,内圈故障和外圈故障的样本熵值变大,即在剔除部分冲击幅值后,阈值r减小,在模式匹配时的相似容限变小,此情况下考虑了冲击幅值区间内部分振动信号的波动,模式匹配值变小,样本熵值变大.故样本熵在衡量振动信号的复杂度时需要考虑在周期性冲击幅值区间内的局域波动情况,由此本文提出基于滚动轴承故障机理的样本熵:先对振动信号进行一阶差分,减小故障状态下振动冲击幅值对计算结果的影响,即考虑冲击幅值间信号的波动,再计算差分后信号的标准差为SD1.本文对阈值r的设定重新验证,选择分析图5 的振动数据,在对振动数据进行差分处理后,相似容限在[0,0.5]区间时,样本熵的变化曲线如图6 所示.

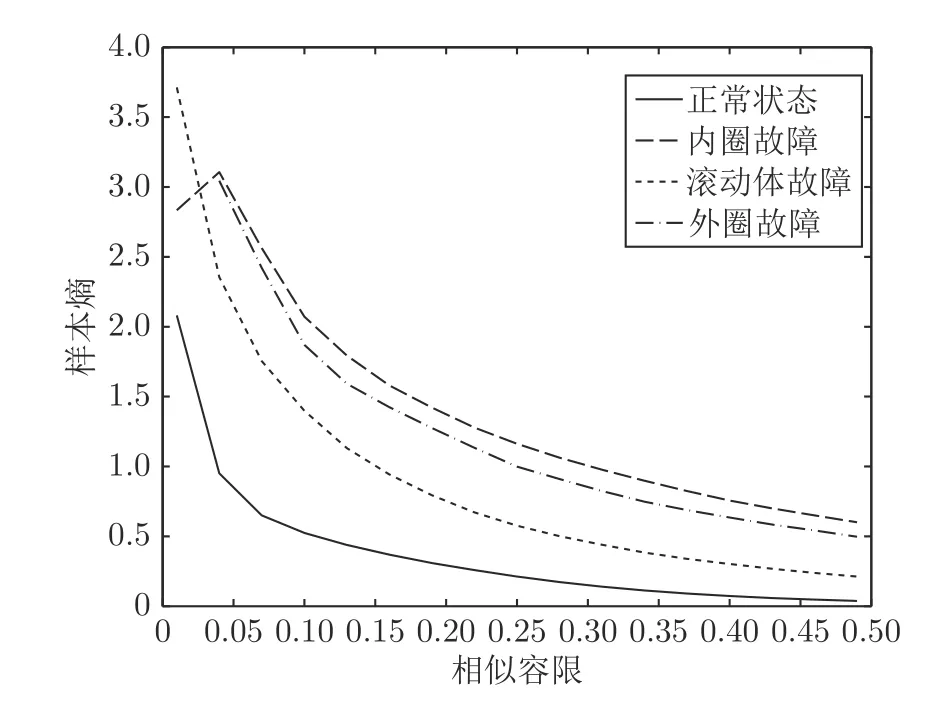
图6 样本熵的变化曲线Fig.6 Evolution of sample entropy

由图6 可以看出,当相似容限在[0.1,0.2]区间时,4 种状态下的区分度都不错.相似容限过大,正常状态和滚动体故障难以区分;相似容限过小,内圈故障和外圈故障混淆严重.故本文选择相似容限为 0.2,设定r=0.2SD1.对于给定的时间序列{x(n)}={x(1),x(2),···,x(N)},基于滚动轴承故障机理的样本熵计算过程如下:

1)由原始信号构建m维向量

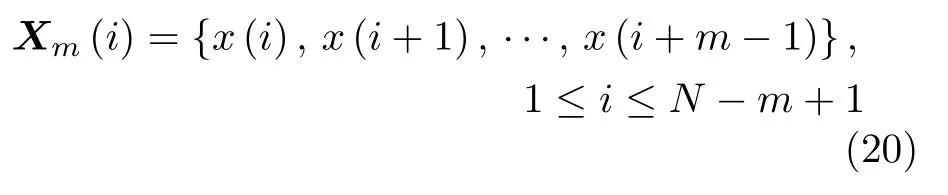
2)定义向量Xm(i)与Xm(j)之间的距离d[Xm(i),Xm(j)]为两者对应元素中最大差值的绝对值.即

3)对于给定的Xm(i),统计Xm(i)与Xm(j)之间距离小于等于r的j(1≤j ≤N -m,j≠i)的数目,并记为Bi.对于 1≤i ≤N -m,定义

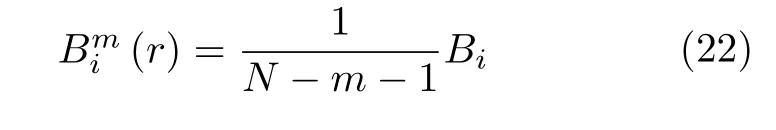
4)定义B(m)(r)为

5)增加维数到m+1,计算Xm+1(i)与Xm+1(j)(1≤j ≤N -m,j≠i)距离小于等于r的个数,记为Ai.(r1)定义为

6)由此,Bm(r)是两个序列在相似容限下匹配m个点的概率,而(r)是两个序列匹配m+1个点的概率,样本熵值为

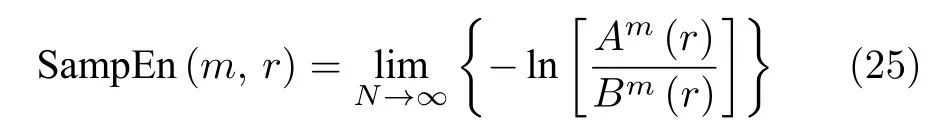
滚动轴承在故障状态下的振动信号反映轴承在运行周期内会出现冲击幅值,信号的波动也更为明显,其中后者也是衡量信号复杂度的重要因素.基于滚动轴承故障机理的样本熵算法的计算规则通过对振动信号进行差分处理,进而更新阈值r,较传统样本熵的计算规则,增加了信号波动在熵值计算中的权重,评判结果也更为合理.依据上述计算规则,4 种状态下振动信号的样本熵为:正常状态时熵值为 0.2923;内圈故障时熵值为 1.3700;滚动体故障时熵值为 0.7557;外圈故障时熵值为 1.2338.可见,正常状态熵值小于故障状态的熵值,这与上述机理分析的滚动轴承在4 种状态下振动信号的复杂度一致,这也说明了本文基于滚动轴承故障机理的样本熵在评判滚动轴承信号复杂度时要优于传统的样本熵算法.

4 基于参数优化VMD和样本熵的滚动轴承故障诊断步骤

针对滚动轴承故障特征提取不丰富而导致诊断识别率低的情况,本文采用遗传变异粒子群算法搜索 VMD 方法的最佳参数组合 [K0,α0],采用参数优化VMD 方法分解原始振动信号得到 IMF 分量,再计算各 IMF 分量的样本熵,最后将样本熵作为特征向量输入 SVM 进行故障分类识别,具体实现步骤如下:

1)获取滚动轴承在内圈故障、滚动体故障、外圈故障和正常状态下的振动信号.

2)遗传变异粒子群算法的参数设置分为粒子群和遗传变异两部分,粒子群参数依据参考文献[31]进行设置;遗传变异操作的 maxAge设置过大会影响算法的收敛速度,本文设置为经验值 2,本文中,D=2,则变异概率q=1/D=0.5,粒子群算法的参数值如表2 所示.

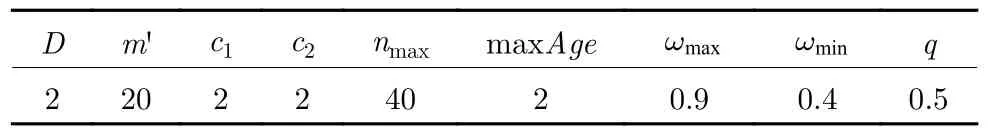
表2 遗传变异粒子群算法的参数值Table 2 The values of parameters in the particle swarm algorithm based on the genetic variation

3)借助遗传变异粒子群算法搜索 VMD 方法在各状态下的最佳参数组合 [K0,α0],设置 VMD方法α=α0,K=K0,采用参数优化的 VMD方法分解各状态下振动信号得到K0个IMF 分量.

4)计算 IMF 分量的样本熵,并构造特征向量.5)采用文献[22]构建的 SVM 模型

式中,X,Y为样本数据的输入,H(X,Y)为SVM 构造的核函数,HGlobal(X,Y)为全局核函数,Hlocal(X,Y)为局部核函数,w(0＜w＜1)为权重因子.本文 SVM 参数设置依据文献[22],选用poly 核函数作为全局核函数,径向基函数(Radial basis function,RBF)核函数作为局部核函数,权重因子w=0.3,惩罚参数为23.67,核函数参数d=1.43,σ=0.35.

6)将特征向量输入 SVM 进行训练,得到各个状态的 SVM 预测模型.

7)采集测试信号,按照3)和 4)构造测试信号的特征向量,将特征向量输入 SVM 预测模型得到诊断识别的结果.

5 仿真实验

本文选用美国凯斯西储大学电气工程实验室的数据源进行仿真实验.选取滚动轴承的负载为 0 kW,损伤直径为 0.1778 mm,转速为 1797 r/min,采样频率为 12 kHz 时内圈故障、滚动体故障、外圈故障和正常状态下的振动信号.以轴承旋转两圈为一组样本,4 种状态的振动信号各选取 120 组样本,其中训练样本 80 组,测试样本 40 组.针对4 种状态的振动信号,遗传变异粒子群算法搜索到的最佳参数组合 [K0,α0]如表3 所示.

表3 最佳参数组合[K0,α0]Table 3 Optimum combination of parameters

根据表3 中最佳参数组合 [K0,α0],设置 VMD方法的α和K,借助参数优化VMD 方法分解训练样本,选取前 3 个 IMF 分量的样本熵,各状态训练样本可以得到 3×80 个熵值.选择每个训练样本中 3 个熵值作为一组特征向量,则可以得到 80组特征向量.将这些特征向量作为输入量,输入 SVM分类器进行训练得到各状态下的预测模型.用训练好的 SVM 分类器对4 种状态下的测试样本分类,测试样本的分类结果如图7 所示.在 SVM 的训练和测试中,用数字标签代表滚动轴承的运行状态,且测试样本的存放次序为:1～40 为内圈故障 (标签 1);41～80 为滚动体故障 (标签 2);81～120 为外圈故障 (标签 3);121～160 为正常状态 (标签 4).

图7 测试样本的分类结果Fig.7 Classification of test samples

由图7 可以看出,采用本文参数优化VMD和样本熵的特征提取方法,轴承状态的诊断正确率达到 100%.选用同样的样本数据,本文采用传统的VMD 分解方法 (K=6,α=2 000)、EMD、LMD和双树复小波变换 (Dual-tree complex wavelets,DTCWT)进行信号分解,借助传统样本熵 (SampEn)构造特征向量,训练 SVM 分类器.用训练好的SVM 分类器对4 种状态下的测试样本分类,其他处理方法的分类结果如表4 所示.

表4 其他处理方法的正确率 (%)Table 4 Correctness of other processing methods (%)

由图7和表4 可以看出,采用本文参数优化VMD和样本熵的特征提取方法,对于同一损伤直径下的不同故障可以正确诊断识别.这说明了本文的方法可以从干扰信号中提取出微小的故障特征,诊断正确率高于传统的 VMD 方法和其他方法.由于不同负载时轴承故障特征区分并不明显,为了进一步检验本文方法的有效性,同样采用 SKF6205型轴承,损伤直径为 0.1778 mm,负载分别为 0 kW,0.75 kW,1.5 kW和2.25 kW 时内圈故障的振动信号,采样频率为 12 kHz.以轴承旋转两圈的数据为一组样本,选取 120 个样本,其中 80 组作为训练样本,40 组作为测试样本.负载不同时内圈故障分别标记为F0,F1,F2和F3.设置 VMD 方法的K=6,α=2 000,并分解不同负载时内圈故障样本信号,计算 IMF 分量的样本熵 (SampEn).该处理方法和本文处理方法对比,测试样本的分类结果如表5 所示.

表5 测试样本的分类正确率 (%)Table 5 Classification accuracy of test samples (%)

采用其他方法分解处理,如 LMD和 EMD,在不同负载时内圈故障的诊断正确率均在 80% 以下,这也验证了 VMD 方法优良的分解特性.从表5 可知,在每个故障类型上,本文参数优化VMD和样本熵的特征提取方法均比给定参数的 VMD 方法诊断正确率高,平均正确率也有明显提高,验证了本文方法可以明显提高故障诊断的正确率.为了深入分析本文方法,当损伤直径为 0.1778 mm,选取负载分别为 0 kW,0.75 kW,1.5 kW和2.25 kW时内圈故障样本信号,样本信号在经过参数优化VMD 方法分解后,本文选取 4 个 IMF 分量样本熵的均值如表6 所示.

设置 VMD 方法的K=6,α=2 000 并分解内圈故障样本信号后,IMF 分量传统样本熵的均值如表7 所示.

负载0 kW,0.75 kW,1.5 kW和2.25 kW 分别对应内圈故障的4 种状态,4 种状态下故障特征不同,复杂度也不同.为了准确诊断这4 种状态,就需要借助 VMD 方法准确提取出4 种状态下的故障特征,构造分解产生的 IMF 分量样本熵作为特征向量,特征向量反映了各状态振动信号的复杂度特征.然而,本文分析了K和α两个参数选取不当时,分解过程会产生欠分解和模态混淆现象,振动信号蕴含的故障特征就不能完整提取重现.表6和表7 分别代表了本文方法和给定参数设置的VMD 方法分解后 IMF 分量熵值的均值,由表7可以看出,给定参数设置的 VMD 方法分解后4 种状态的熵值区分不明显,即给定参数设置的 VMD方法没有提取出各状态下振动信号蕴含的丰富故障特征,传统样本熵计算的熵值不能反映4 种状态振动信号的复杂度,且特征向量过于相似,影响了SVM 的训练过程.由表6 可以看出,本文提出的参数优化VMD和样本熵的特征提取方法可以区分内圈故障的4 种状态,熵值区分明显,即参数优化的 VMD 方法可以很好地提取各状态下蕴含的故障特征,且样本熵构造的特征向量具有较大差异性,提高了 SVM 的诊断识别率,证明了本文方法可以明显提高滚动轴承故障诊断的正确率.

表6 IMF 分量样本熵的均值Table 6 The mean of IMF sample entropy

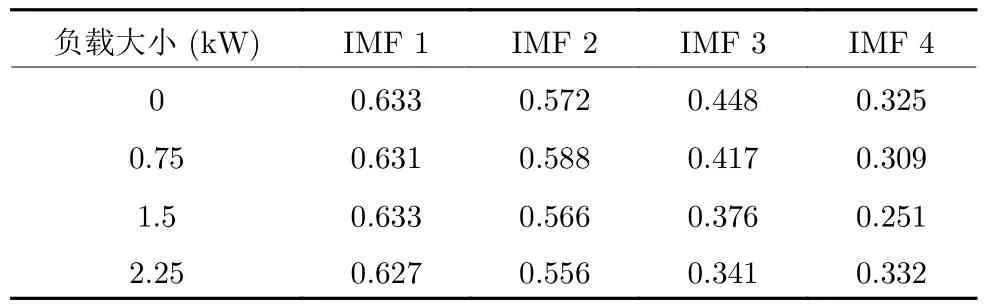
表7 IMF 分量传统样本熵的均值Table 7 The mean of IMF traditional sample entropy

6 结束语

本文提出了基于参数优化VMD和样本熵的特征提取方法,借助参数优化的 VMD 方法分解振动信号,对分解后的 IMF 分量求取样本熵,作为特征向量输入 SVM,实现滚动轴承的故障诊断识别.VMD 方法的分解效果受限于惩罚因子和分解个数的选择,故借助遗传变异粒子群算法进行参数优化.参数优化的 VMD 方法与给定参数设置的 VMD方法相比,提取的故障特征更为丰富.基于滚动轴承故障机理的样本熵算法在衡量振动信号的复杂度时,衡量结果与机理分析的结果一致,有利于对轴承状态的诊断判别.仿真实验表明,采用本文参数优化VMD和样本熵的特征提取方法,滚动轴承的故障诊断准确率有明显的提高.

致谢

感谢美国凯斯西储大学电气工程实验室的学者,正是他们严谨的实验数据,为本文提供了坚实的基础.