OTH 雷达图像的粗糙度指标及用于射频干扰自适应抑制

罗忠涛 郭人铭 郭杰 何子述 卢琨

现代雷达普遍采用动目标检测技术,信号检测通常在距离-多普勒(Range-Doppler,RD)图中进行.当雷达信号带宽内出现干扰时,干扰会叠加到RD 单元幅度上,从而影响目标检测.该现象在超视距(Over-the-horizon,OTH)雷达中经常遇到[1].

OTH 雷达工作在高频段,易受其他设备信号干扰的影响.射频干扰(Radio frequency interference,RFI)被雷达接收并经信号处理后,会在RD图上表现出不同形态,影响目标检测甚至是海杂波谱探测[1-2].干扰抑制一直受到高频雷达研究的关注,学者们也提出了基于不同原理的干扰抑制方法[3-8].然而,由于天波雷达中干扰和杂波特性均为未知,传统干扰抑制方法都不能从理论上证明某方法最优,也难以提出明确的优化方向.

事实上,基于分析RD 图的经验发现,尽管从数据特征上难以评判RD 图的优劣,但用人眼观察RD 图却很容易有直观的评判.如图1 所示,噪声区域像背景底色;海杂波区域是不规则边缘的带状区域;窄带干扰表现为平行于距离维的高亮直线;宽带干扰表现为遍布全图的条纹状[5].当干扰抑制不充分或过度抑制时,RD 图形态也会变化.尽管此类变化从传统的信号处理角度来说难以表征和量化,从人眼和图像的角度却可以直观发现.

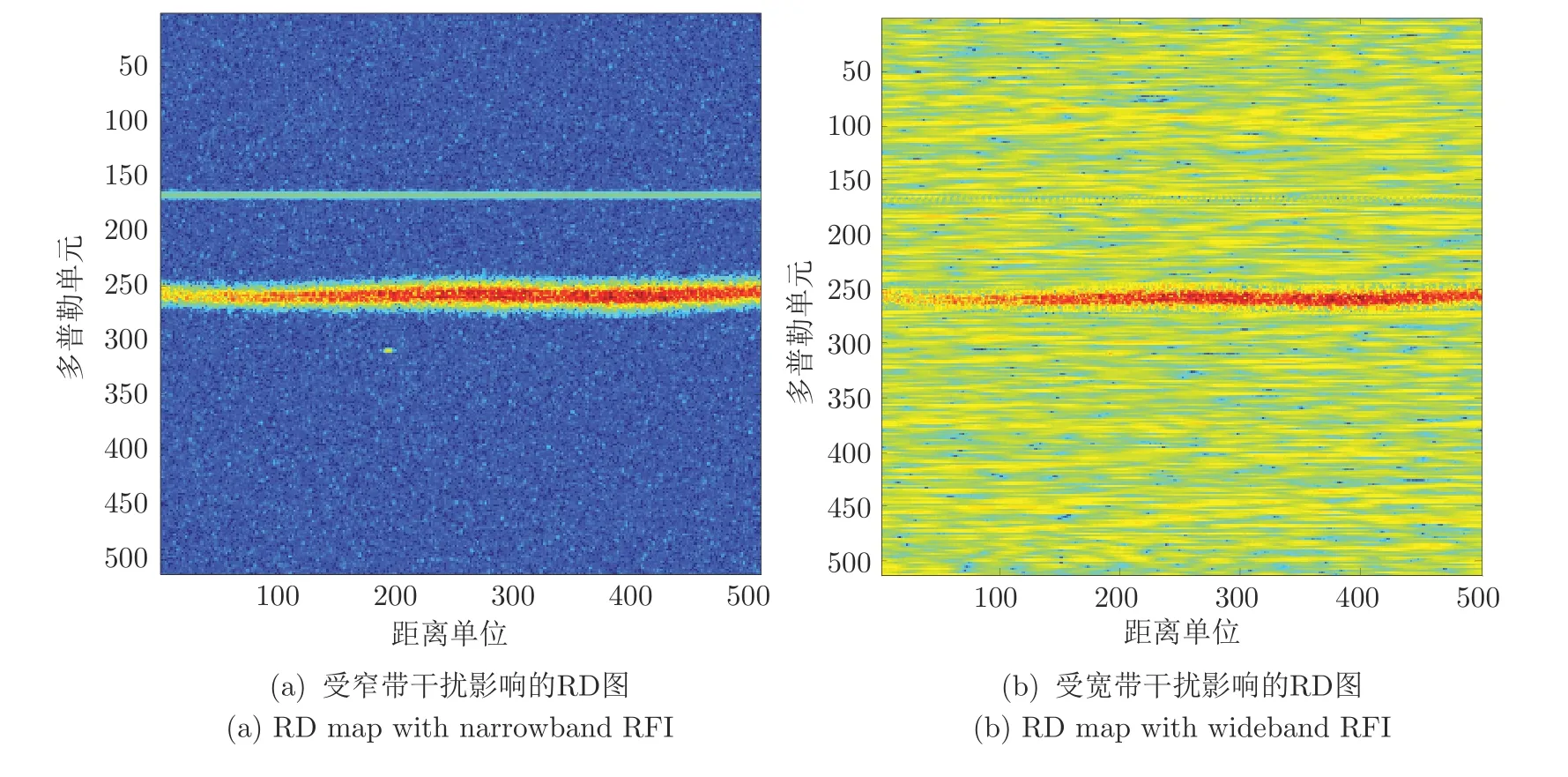
图1 OTH 雷达RD图Fig.1 RD maps of OTH radar

本文拟从图像分析的角度,研究OTH 雷达的RD 图像质量及干扰问题.之前,作者研究直线检测技术在OTH 雷达中的应用,如在文献[9]中提出快-慢时间图中检测瞬态干扰直线,在文献[10]中提出了RD 灰度图中检测窄带干扰直线.本文考虑从图像分析角度,分析RD 图像的特征与形态,通过提取图像的纹理特征来判断RD 图的质量.

纹理是图像的一个重要特征,可用于分析许多类型的图像,如自然图像、遥感图像、医疗图像等.作为一种视觉特征,纹理分析的方法有多种,如空间自相关法、共生矩阵法、Tamura 方法等.其中,Tamura 纹理由Tamura 等于1978 年提出[11],它基于人类对纹理的视觉感知,侧重对图像全局特征的提取,其特征量中对应于心理学角度上纹理特征的6 种属性,即粗糙度、对比度、方向度、线性度、规整度和粗略度.

在Tamura 纹理中,粗糙度(Coarseness)是最基本的纹理特征,可以直观反映人眼对图像粗糙程度的感知,常用于基于内容的图像检索与评估、异常纹理检测等.例如,文献[12]通过提取视频帧Tamura 纹理特征来检测数字视频是否被复制移动或篡改;文献[13]提出基于金属零件表面图像Tamura 纹理的粗糙度、对比度和方向度来识别不同工艺加工的零件;文献[14]提出基于水下目标功率谱图的Tamura 纹理的粗糙度和对比度,检测与识别水下目标速度的高低.文献[15]提出使用Tamura 纹理特征实现对嘈杂环境和不良照明下车牌的准确定位.文献[16]提出基于纹理的障碍物检测算法,Tamura 方法比空间自相关法和共生矩阵法更加稳健.在生物医学图像分析中,Tamura 纹理可用于表征研究对象的形状和内部结构,并判断不同形态器官组织代表的信息[17].总之,Tamura 粗糙度在图像分析中有着广泛应用.

截至目前,尚无文献对Tamura 纹理和RD 图像结合展开研究.本文将开展创新性工作,首次讨论将Tamura 纹理粗糙度用于OTH 雷达RD 图像,并分析其合理性.其次,考虑RD 图像可能受干扰的情形,分析粗糙度与干扰情形之间的联系.最后给出粗糙度的使用举例,以粗糙度作为指标实现射频干扰的自适应抑制.

1 RD 图像与粗糙度计算

本小节介绍OTH 雷达的RD 图处理方法,利用灰度变换函数将其转化为灰度图,再给出Tamura粗糙度的计算方法.

1.1 RD 图与灰度图

设OTH 雷达接收阵列为K个阵元组成的均匀线阵,一个相干处理间隔内有N个采样点,雷达接收数据排列为矩阵XR∈CK×N.采用K维权向量a对XR进行波束形成,输出为时域数据xR=a×XR.对时域数据xR进行脉冲压缩和多普勒处理,即可得到RD 矩阵Z∈CP×M.其中,P为一个相干处理间隔内的积累周期数,M为单周期内的采样点数.将RD 矩阵Z的值按照幅度dB值显示,即可得到RD图[5].

考虑获得RD 图后进入图像分析阶段.首先将RD 图转化为灰度图.人们在观察时,一般采用dB值来呈现RD 图,以便显示绝对幅度比海杂波小得多的噪声和目标.

本文采用基于对数函数的灰度变换方法,将常规RD 图转化为RD 灰度图.对数变换中可设置合理的最小值,以控制原数据的动态范围.例如,设置动态范围为bdB,则RD 矩阵元素不会小于最小值

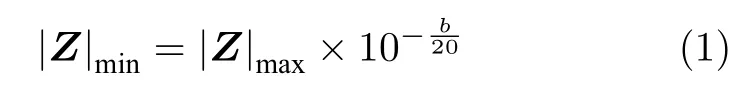
其中,|Z|max表示矩阵Z中的最大模值.总的灰度变换函数可以表示为

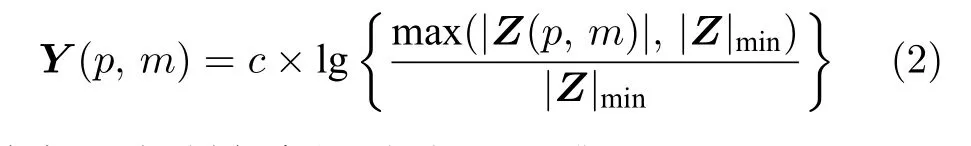
其中,c控制灰度级,例如256 或64.

经过灰度变换,原RD 矩阵Z或RD 图转化为RD 灰度图,原距离-多普勒单元 (p,m)的幅度转换成灰度图中像素点 (p,m)的灰度值.

1.2 粗糙度的计算

粗糙度是反映纹理中粒度的一个量,是最基本的纹理特征.粗糙度描述了一幅图像平均的粗糙程度.针对灰度图Y(p,m),粗糙度的计算可分为以下3 个步骤.

步骤 1.计算图像中大小为 2k×2k像素的活动窗口中像素的平均强度值,即

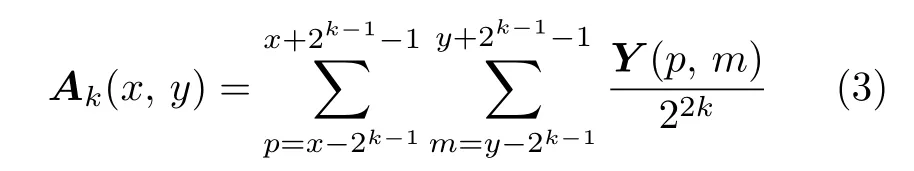
其中,k=1,···,K控制活动窗口大小,一般K值在2～6 之间;Y(p,m)为像素点 (p,m)的灰度值.

步骤 2.计算每个像素点在水平和垂直方向上互不重叠的窗口之间的平均强度差

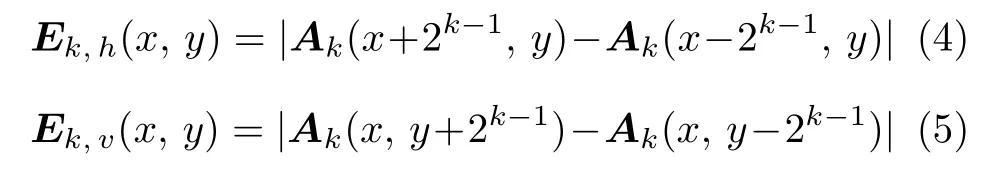
其中,Ek,h(x,y)代表水平方向差值,Ek,v(x,y)代表垂直方向差值.对于每个像素,假设kbest是使Ek,h(x,y)和Ek,v(x,y)中较大者达到最大的k值,对应最佳尺寸

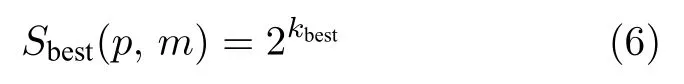
步骤 3.粗糙度计算为整幅图最佳尺寸的平均值

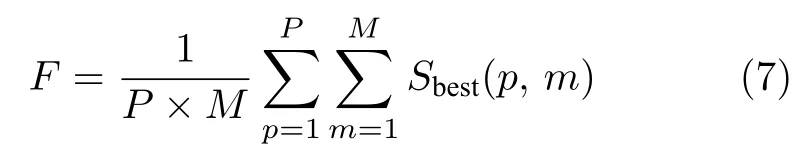
基于OTH 雷达RD 图转化的灰度图,经过步骤1～3 运算,即可得到该图的粗糙度.考虑到一般情况下,OTH 雷达重点关注目标检测,而RD 图中非海杂波即噪声区域才是潜在的目标检测区域.因此,可采用RD 灰度图的海杂波区域以外(例如±20 倍Bragg 频率外[5])区域来计算粗糙度.

2 RD 灰度图粗糙度分析

本文提出将粗糙度作为一个指标,来衡量RD灰度图质量.那么,需要讨论粗糙度的影响因素和应具有的性质.首先,粗糙度应当稳健,因为各相干处理间隔的数据功率有所不同,生成灰度图时灰度转换函数含有人为参数.其次,粗糙度需要能够表征RD 图质量,即准确反映RD 图是否受干扰影响、完全抑制或过度抑制等情况.

2.1 灰度转换的影响

首先分析灰度变换对粗糙度指标的影响.将RD 图经灰度变换函数转换为灰度图像的过程中,动态范围和灰度级都会影响RD 灰度图,从而影响灰度图的粗糙度.

仿真一组相干处理间隔为5.12 s 的海杂波数据,再结合无干扰、宽带干扰和窄带干扰数据,分别处理得到RD 图,再由灰度变换生成RD 灰度图,设置灰度级为256.当未设置动态范围时,不同干扰情况的RD 灰度图为图2(a)～2(c);设置动态范围b=80dB 时,对应的灰度图分别是图2(d)～2(f).可以看到,设置动态范围后,大部分像素灰度值下降,海杂波、目标与背景噪声的对比更为明显,更利于视觉观察.

横向比较图2 中的3 幅图.在图2(a)与2(d)中,RD 图无干扰,噪声区域的幅度分布均匀,是理想的噪声形态.目标清晰显示,可认为是RD 图像质量最佳.在图2(b)与2(e)中,RD 图存在窄带射频干扰直线,目标检测也会受影响,图像质量较差.在图2(c)与2(f)中,宽带射频干扰遍布RD 图,全图区域布满条纹,目标难以观察,可认为图像质量很差.

针对图2 中各种情形下的数据,采用K=4 以及灰度级256、64和32,粗糙度计算结果如表1.

图2 不同干扰情形下的RD 灰度图:(a)～(c)分别表示无动态范围转换的无干扰、有窄带射频干扰、有宽带射频干扰的RD灰度图;(d)～(f)分别表示对应的动态范围为80 dB 转换的RD 灰度图Fig.2 RD gray-scale images:(a)～(c)are images without dynamic range conversion,for no RFI,narrowband RFI,and wideband RFI,respectively;(d)～(f)are corresponding images with dynamic range conversion for 80 dB

1)对表1 进行横向分析.对于每种干扰状态的粗糙度,在不同灰度级256 或64 或32 下,有动态范围比无动态范围时稍小一点,可认为是基本相同.说明在不同灰度图转换方式下,每种干扰状态的粗糙度是稳健的.

2)对表1 进行纵向分析.不含干扰时粗糙度最低,含窄带射频干扰时次之,宽带射频干扰的粗糙度最高.从是否有利于目标检测的图像质量观点来看,可发现一个规律:粗糙度越低,图像质量越高,噪声区域越干净,越利于目标检测;反之,粗糙度越高,图像质量越差,越不利于目标检测.

表1 不同干扰类型的RD 图粗糙度Table 1 Coarseness of RD images for various kinds of interference

2.2 干扰程度的影响

下面分析干扰情况对粗糙度的影响,观察粗糙度是否能够准确表现干扰严重程度和抑制程度.当OTH 雷达RD 图中含干扰时,干扰严重程度及是否充分抑制,会在RD 灰度图上表现出不同的形态,而不同的形态所对应的粗糙度值也不同.图3 仿真不同干扰情况和抑制情况,分别为无干扰、有宽带射频干扰及干扰抑制程度不同的RD 灰度图.图3(a)～3(e)表示灰度转换时无动态范围,图3(f)～3(j)表示灰度转换有动态范围80 dB.干扰抑制算法采用了文献[18]中的滤波器设计方法,未完全抑制或完全抑制效果是由过大或过小的相似度值产生.

可以观察到,当图3(a)和3(f)中RD 图无干扰时,噪声区域的幅度分布较均匀,目标可观察;当图3(b)和3(g)中RD 图含宽带射频干扰时,目标难以观察.图3(a)和3(f)经滤波器设计抑制干扰后,图3(c)和3(h)是干扰未完全抑制的RD 灰度图,可见噪声区域的纹理粗糙;图3(d)和3(i)是干扰完全抑制的RD 灰度图,可见噪声区域幅度分布较均匀,目标可观察;图3(e)和3(j)是干扰过度抑制的RD灰度图,可见噪声区域纹理较粗糙,目标被掩盖.

对图3 分别计算当灰度级为256、64和32 时的粗糙度,计算结果如表2 所示.从表2 可以看到,无干扰时,粗糙度数值处于最低;有干扰但被完全抑制时,粗糙度次之;有干扰且未抑制时,粗糙度最高;当干扰未完全抑制或者过度抑制时,噪声区域的粗糙度介于最优抑制和未抑制之间.此外,有无动态范围转换或灰度级大小,对粗糙度基本无影响.

表2 不同干扰抑制程度的RD 图粗糙度Table 2 Coarseness of RD images for various levels of RFI suppression

2.3 目标数量的影响

接下来分析目标数量对粗糙度的影响.模拟不同径向速度和距离的目标回波,与海杂波一起组成雷达回波.在无干扰的情况下,采用传统脉冲压缩和多普勒处理,输出RD 图如图4.总体上目标位置呈现出随机分布,每个目标形成了一个光斑,占据了多个距离-多普勒单元,可视为反映了目标回波在电离层等影响下距离和多普勒维的旁瓣展宽.对于目标像素点会在多大程度上影响粗糙度,可以通过测量不同目标情况对应的粗糙度进行观察和衡量.考虑图3 中的干扰有无和抑制程度的不同情况,再加上目标数量变化的因素,组成不同干扰、目标和抑制的多种组合,处理得到各自的RD 灰度图,并计算其粗糙度.

图3 不同干扰抑制结果的RD 灰度图:(a)～(e)分别表示无动态范围转换的无干扰、有宽带干扰、干扰未完全抑制、干扰完全抑制、干扰过度抑制的RD 灰度图;(f)～(j)分别表示对应的动态范围为80 dB 转换的RD 灰度图Fig.3 RD gray-scale image for various interference suppression results:(a)～(e)are images without interference,broadband RFI,incomplete suppression,complete suppression,and excessive suppression,without dynamic range conversion;(f)～(j)are the corresponding images with dynamic range conversion for 80 dB

图4 在无干扰的海杂波数据中加入目标回波后,RD 图中20 个目标的距离-多普勒单元位置Fig.4 The position of 20 targets in the RD map without any RFI

分别以目标数量为0,1,5,10,15,20 为例,考虑图3(f)～3(j)中干扰和抑制处理情况,得到256灰度级动态范围为 80 dB 的RD 灰度图,计算粗糙度的结果如表3 所示.

在表3 中,当存在干扰但无抑制或未充分抑制时,目标对粗糙度基本无影响.这并不难理解,目标幅度往往较干扰更低故而被干扰掩盖掉,因此对整图的粗糙度未形成明显影响.

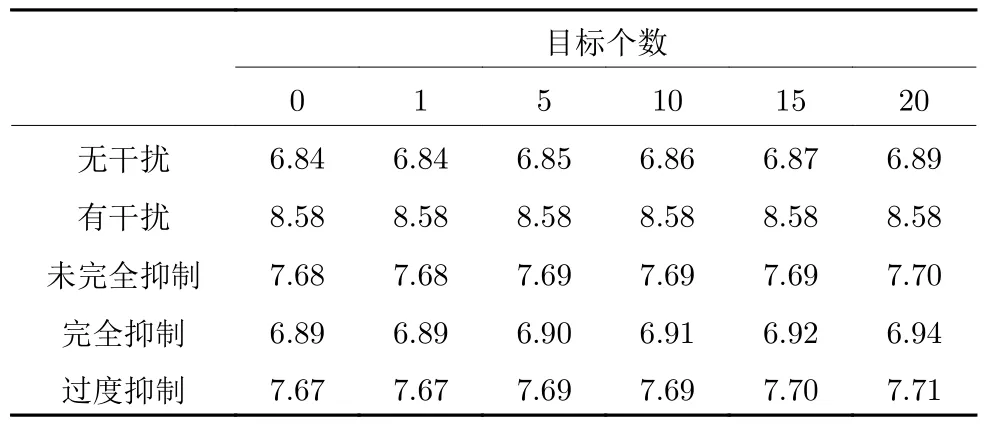
表3 不同目标情况下RD 图的粗糙度Table 3 Coarseness of RD images of various targets

当干扰不存在,以及干扰存在且完全或过度抑制时,目标数量对RD 图的粗糙度有了一定的影响.由表3 可以看到,当目标数量由0 增至20,无干扰下的粗糙度由6.84 增长到6.89;干扰完全抑制下的粗糙度由6.89 增长至6.94.综上所述,随目标数据增加,粗糙度的增长幅度很小,不到粗糙度值的1%.

最后从纵向看表3.在相同目标个数下,无干扰情况具有最小的粗糙度;有干扰但被完全抑制时,粗糙度次之;有干扰且未抑制时,粗糙度最高.这些仿真结果与第2.2 节中无目标时是一致的.此外,改变动态范围或灰度级大小,对于目标存在下的粗糙度结果基本无影响.因此,可以说目标对于粗糙度的影响很小.

2.4 粗糙度分析小结

除以上仿真外,作者基于实测的OTH 雷达数据,进行了RD 灰度图转换和纹理粗糙度分析,其结果与上面的仿真结果基本吻合.结合已有的研究,OTH 雷达图像粗糙度分析的结论主要有:

1)一组OTH 雷达相干处理间隔内数据,生成RD 灰度图并计算Tamura 纹理粗糙度,该粗糙度数值在灰度变换函数参数改变时基本不变.这说明,针对不同类型和状态下的OTH 雷达数据,粗糙度可以作为一个稳健的衡量指标.

2)以目标检测环境是否理想的视角来看,纹理粗糙度能够正确反映RD 灰度图的理想程度,不受干扰时的理想RD 图粗糙度小,受干扰时的RD 图粗糙度数值大,最优抑制的RD 图粗糙度与无干扰时粗糙度很接近.

3)纹理粗糙度作为衡量指标,基本不受目标存在与否及其数量的影响.目标的存在既不会明显改变粗糙度,也没有改变干扰抑制情况与粗糙度大小的对应次序.因此,粗糙度可以正确地衡量有目标时的RD 图理想程度.

综上,纹理粗糙度表现稳健,能够正确反映RD 灰度图是否理想,可作为RD 图质量的指标.以粗糙度为指标,OTH 雷达不仅可以评估雷达工作状态,还可帮助提升信号处理算法,实现自适应优化处理.

3 粗糙度用于自适应干扰抑制

本文以基于滤波器设计的射频干扰抑制为例,展示粗糙度指标如何使干扰抑制变得自适应.以此例说明粗糙度在OTH 雷达信号处理中具有很大的应用潜力.

针对射频干扰,传统抑制算法虽多,但由于干扰、噪声及杂波参数未知,没有理论指标作参考,不能确认是否取得自适应最优效果.在引入粗糙度指标后,以实现噪声区域(非杂波区域)的指标最小化为目标,可对射频干扰进行自适应抑制处理,避免干扰抑制不充分或过度抑制的情况.

3.1 自适应优化干扰抑制

粗糙度指标能够自适应地判断和评价干扰情况.以文献[18]中固定相似度约束下设计滤波器的干扰抑制方法为例,基于粗糙度指标优化的自适应干扰抑制方案如图5.其中,对RD 图粗糙度的计算与优化,构成了一个循环迭代过程.如图5 所示,首先将传统的RD 图转化为灰度图像,然后计算Tamura 纹理粗糙度.当粗糙度指标未达到最小时,该方案会继续优化滤波器参数,循环迭代直至粗糙度达到最小.

图5 干扰抑制自适应优化流程框图Fig.5 Flow chart of adaptive RFI suppression

借助于图像粗糙度,自适应干扰抑制算法具体流程如算法1 所示.其中,干扰抑制算法的参数是相似度ε,取值范围为 (0,1].本文采用一个简单的迭代方法:设置初始值ε0=1,步长△ε为一个较小值,如0.01;令ε逐步减小,表示抑制程度在增加,直到取得最小粗糙度值.相比传统干扰抑制方法[8]设定固定相似度0.8,本文方法以取得最优相似度εopt,对应于最小粗糙度值,实现干扰抑制最优化.

算法 1.滤波器自适应干扰抑制优化算法

步骤 1.设置滤波器参数ε的优化步长为△ε,阈值比率η=0.01.初始化迭代次数j=0,对应滤波器参数为ε0=1,计算干扰噪声区域的粗糙度值F0.

步骤 2.j=j+1,εj=εj-1-△ε,根据εj设计滤波器并抑制干扰,计算其RD 灰度图的粗糙度Fj.

步骤 3.计算粗糙度差值△F=Fj-1-Fj.判断:若△F/Fj-1＜η,取得最优抑制,转至步骤4;否则,转至步骤2.

步骤 4.若△F＜0,εopt=εj-1;否则,εopt=εj.输出εopt对应最优滤波器和干扰抑制结果.

3.2 自适应干扰抑制仿真

采用MATLAB 软件仿真和处理天波雷达数据,验证本文提出的粗糙度纹理特征判断图像质量和自适应干扰抑制方法.设雷达发射线性调频连续波,波形参数为带宽20 kHz,采样频率50 kHz,波形周期 10 ms,相干积累周期数512.模拟射频干扰,与目标回波及海杂波相加为雷达接收数据,采用脉冲压缩和快速傅里叶变换做多普勒处理,设置动态范围为80 dB,所得RD 图如图6(a)所示.图中每个像素点即距离-多普勒单元的多普勒维长度约为0.2 Hz,距离维长度约为 3km.注意,图1～3中RD图均基于此组参数产生.

图6 基于不同ε参数下的RD 灰度图与粗糙度Fig.6 RD gray-scale image and coarseness for varyingε

由图6(a)可见,宽带射频干扰存在时图像纹理粗糙,噪声区域的纹理特性不均匀.采用本文方法计算噪声区域的粗糙度.首先,以动态范围 80 dB和灰度级256,将RD 图转换为灰度图.然后,取20 倍Bragg 频率以外的区域为噪声区域,计算噪声区域粗糙度为F0=8.58.

采用算法1,设置粗糙度计算参数K=4,相似度初始值ε0=1,优化步长△ε=0.01,对干扰抑制进行自适应优化.图7 中用正方形标记的虚线给出了自适应算法的迭代过程.当迭代次数j由0 增加到5 时,ε由1 减小到0.95,粗糙度在逐步减小,对应干扰抑制效果也在优化;当j=6即ε=0.94 时,粗糙度增大,说明进入过度抑制阶段.因此迭代终止,最优抑制停在ε=0.95,此时粗糙度值为6.89,非常接近无干扰时粗糙度6.84.比较图6(c)与图2(d),可以看到,本文最优抑制结果与无干扰时RD 图像非常接近.

仿真其他相似度ε值对应的粗糙度,如图7 中实线所示.可以看到,粗糙度的变化趋势是先减后增,表明粗糙度确实存在最小值且容易寻找.4 个典型相似度参数ε值所对应的RD 灰度图如图6 所示,其中图6(d)为白化滤波器即ε=0.76 的结果.可以看到,粗糙度确实能够正确反映人们对RD 灰度图质量的视觉效果.此外,改变K值为3和5,粗糙度与相似度的对应关系保持不变,如图7 所示.

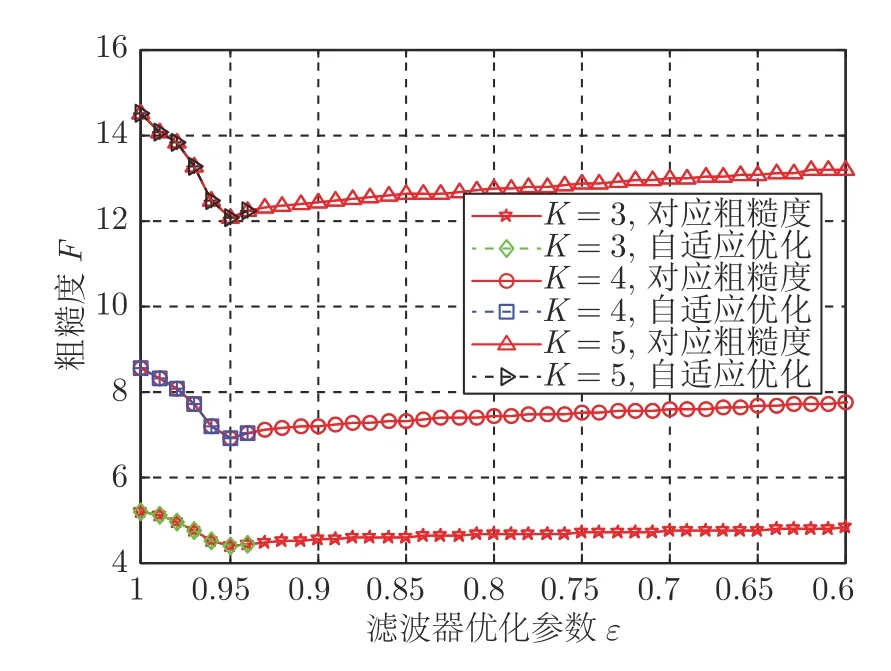
图7 粗糙度F随ε的变化趋势Fig.7 The coarsenessFversusε

为观察粗糙度更多细节,图8 画出了K分别为3,4,5 时最佳尺寸参数kbest的比例随ε的变化.三幅图具有共同特点:kbest=1 比例总是随干扰抑制优化(ε从1 到0.95)而增大,随抑制恶化(ε从0.95 到0.94)而减小.当K=5时,kbest=4,5 比例的增减趋势与kbest=1,2恰好相反;当K=4 时,kbest=4比例与kbest=1 恰好相反.由式(6)和式(7)可见,kbest越小则粗糙度越小,故小kbest值的比例与粗糙度增减趋势正好相反.这与仿真图相吻合:针对同一K值,图8中kbest=1 比例越大,对应图7中粗糙度越小.结合图7和图8 可见,K=4和5对应的粗糙度变化趋势比K=3 更加明显,故更适合用来计算粗糙度.

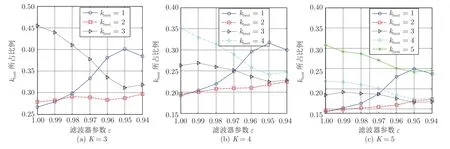
图8 不同K值下ε变化时的kbest比例Fig.8 The ratio ofkbestversusεfor varyingK

此外,针对多目标场景的仿真结果表明,目标对粗糙度影响很小,不改变粗糙度与相似度的变化趋势,本文干扰抑制方法依然可行.另外,本文算法也用于实测OTH 雷达数据的干扰抑制,处理结果与本文仿真相似.由此说明,本文提出的粗糙度指标和自适应滤波器设计算法,可以有效抑制射频干扰,达到最优抑制效果.本文抑制方案还可采用线搜索方法来迭代优化参数,从而减少运算量,未来工作也将应用到更多实测数据处理中.

4 结束语

针对OTH 雷达图像,本文首次提出计算RD图中非杂波区域的Tamura 纹理粗糙度,作为RD图像质量的评估指标.粗糙度指标能够反映干扰抑制的不同程度,为干扰抑制提供了合理的优化方向.结合RD 灰度图的Tamura 纹理粗糙度,能够设计出具有自适应优化能力的干扰抑制算法.实验结果表明,借助于Tamura 纹理粗糙度优化,自适应干扰抑制算法能够取得最佳干扰抑制效果.作为OTH 雷达RD 图像质量评估指标,Tamura 粗糙度有着很好的应用潜力,将在未来研究中开发出更多应用.