基于结构方程模型的危险品道路运输影响因素研究*

□ 展定玉，杨延梅，李 伟

( 1.兰州交通大学 交通运输学院，甘肃 兰州 730070；2.大秦铁路股份有限公司 榆次站，山西 晋中 030600)

危险品由于其特殊的性质，流通过程中极易在各种外界因素的作用下发生安全事故，造成人员伤亡和财产损失的严重后果。2019年7月至2020年8月，我国安全生产事故共计484件，死亡人数1585人，其中危险货物运输事故196件，占比40.5%；死亡人数657人，占比44.24%。因此，扼制造成危险品运输事故的主要因素对预防事故的发生有很大的理论与实践意义。

国内对货物运输事故的分析研究主要集中在影响因素研究、预警模型风险评价或管理研究。胡立伟等[1]通过建立货车交通事故风险因素网络模型对人、车、环、管四个方面的影响因素进行识别判断，得到关键风险因素。沈小燕等[2]通过对比决策树、支持向量机和多次感知器对危险货物道路运输事故数据进行分析，得到危险货物道路运输事故严重程度的影响因素。吴迪[3]依据贝叶斯网络建立了危险货物道路运输事故预测模型。马晓丽等[4]通过对风险因素的分析建立有序Logit模型，利用距离加权法得到危险货物运输过程中的风险值。张帅等[5]从“人车路货”四个方面对影响危险品运输的元素进行分析，提出相应的解决方案。苏磊[6]采用层次分析法得到不同运输方式下的事故权重，运用统计特征分析等方法构建危险品运输事故体系并对关键因素进行分析。张运胜等[7]在大数据分析基础上研究危险品运输风险管理机制。张江石等[8]利用联合概率公式计算情景发生概率，实现危险化学品事故中关键情景的推演。郭健等[9]依据数据信息融合对事故状态进行预判。

国内研究多数是针对单一或部分因素进行分析，得到其在系统中所占权重或影响危险品流通安全的关键性因素，对于各影响因素之间相互关系的研究仍具有一定的局限性，在指标体系选取时较宽泛，容易导致结果不精确。程谦等[10-12]通过结构方程模型对城市轨道交通服务质量影响因素、高速铁路客运服务质量、城市常规公交满意度等方面进行评价研究，虽然模型组成信度、收敛效度较好，但通过调查问卷方式获得的数据主观性较强。鉴于此，本文通过整理危险品事故数据，获得一年来危险品事故数量493件(数据来源：化学品事故信息网)，为保证数据的有效性，将缺失的数据筛除，最终得到154件数据作为研究对象，设立5个潜变量和19个观察变量，以事故观察变量为最终结果，通过验证性因素分析对影响因素进行选取，利用通过筛选后的15个影响因素建立结构模型，数据显示对事故的解释程度达到70%，为危险品运输和安全预警研究提供一定的理论支持。

1 因素及数据分析

1.1 因素分析

危险品事故发生主要有人、运输设备、环境、危险品、管理这五方面的原因，通过事故分析绘制影响因素如图1所示。车辆罐体状态包括车辆定期检查、运行里程、使用年限。车辆装载设施故障方式分内部原因和外部原因，内部原因包括车体问题(车体突发故障如爆胎、刹车失灵、打滑等)和装载设施问题(罐体意外破损或因年久失修造成货物泄露等)；外部原因为因驾驶人员操作失误造成的侧翻、追尾等情况。路面情况1为路面干燥程度；路面情况2为路面坑洼程度、障碍物严重程度。明亮时间段如图2所示。

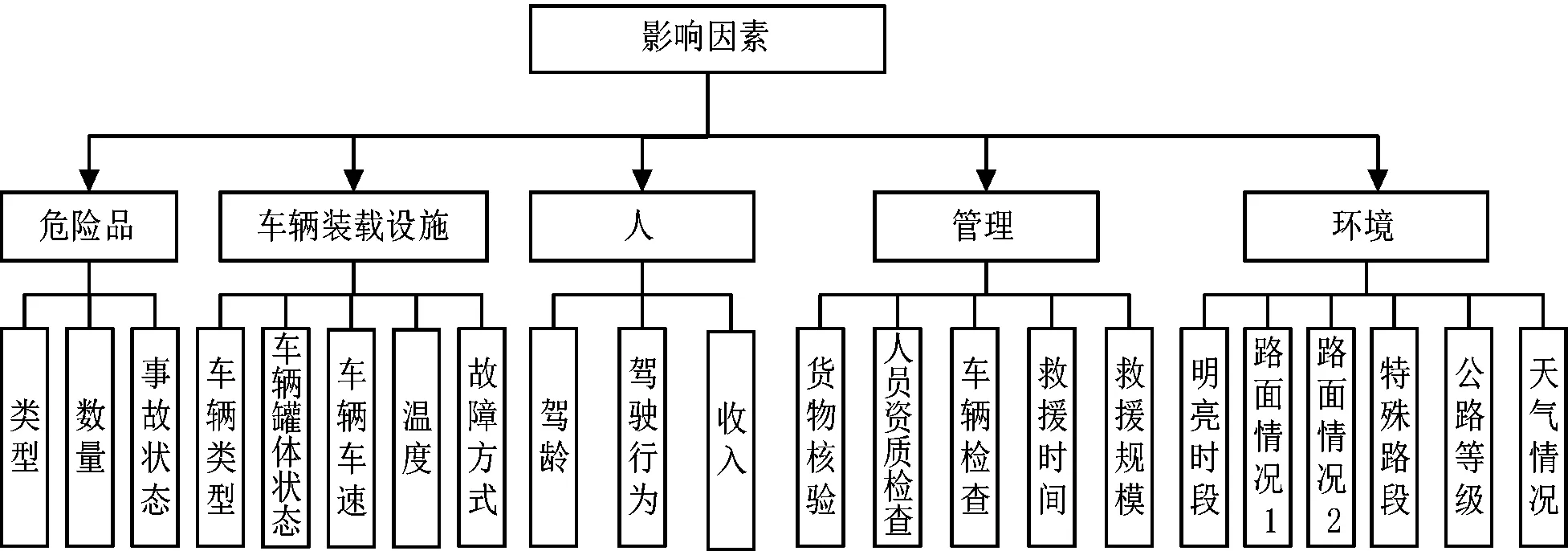
图1 影响因素

图2 明亮程度时间段

1.2 数据分析

通过原始事故数据分析(部分因素数据缺失)得到一年来各省份事故发生数量如表1所示，上海、山东、河南、广东发生事故的数量最多，安徽、湖北、湖南、四川、浙江次之。表2、图3为事故发生时间段分析，从中可以看出事故发生时间段呈周期性变化，午高峰期间事故发生最多，零时区间发生事故次之。另外，遇高温爆炸1件，因道路标志标线不合理发生事故1件。天气分析如表3所示。温度方面：最低气温-16℃，最高气温38℃，各温度区间发生事故的数量如表4所示，极寒下事故发生较少，常温、高温下事故发生最多。根据事故分析划分人员驾驶行为如图4所示，数值按导致事故后果严重程度分级。其他数据分析如表5所示。根据事故分析得到最终因素变量表如表6所示。

表1 各省份事故数量

表2 时间段事故数量表

表3 天气事故数量表

表4 各温度段事故数量表

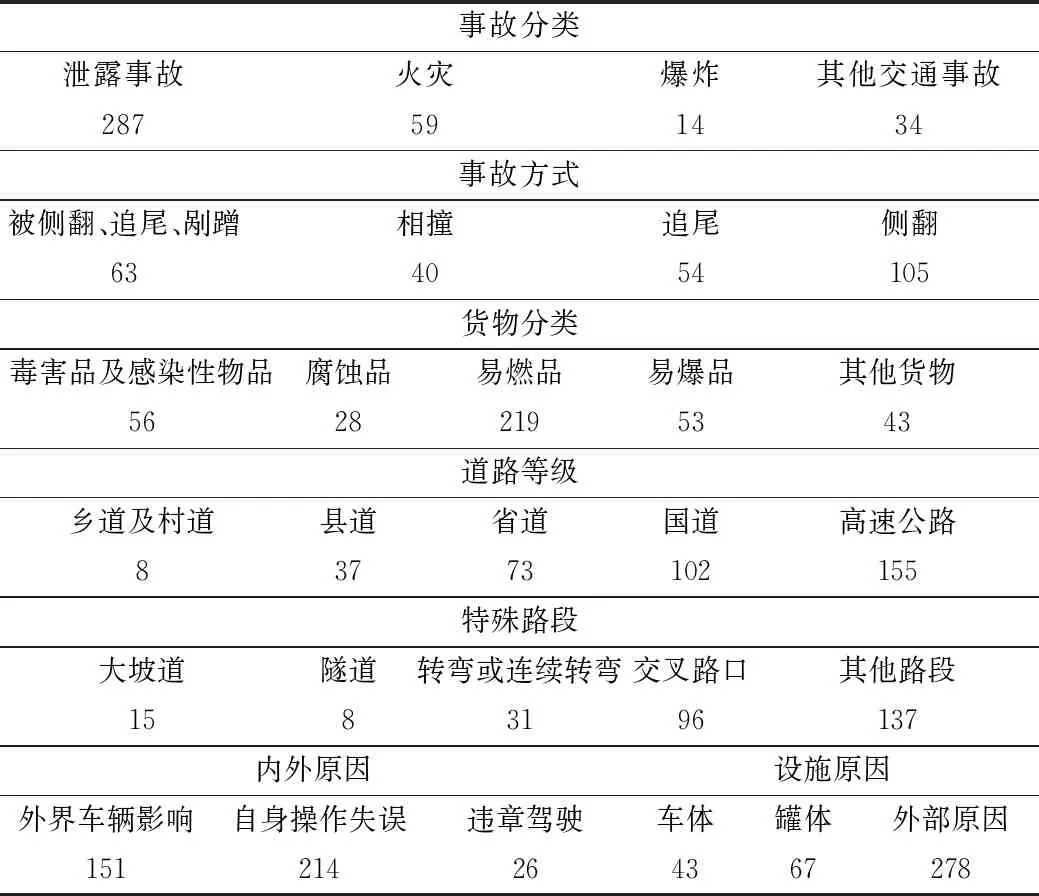
表5 数据分析

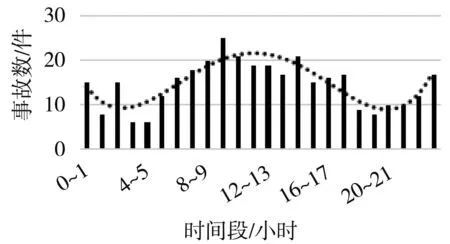
图3 时间段分析

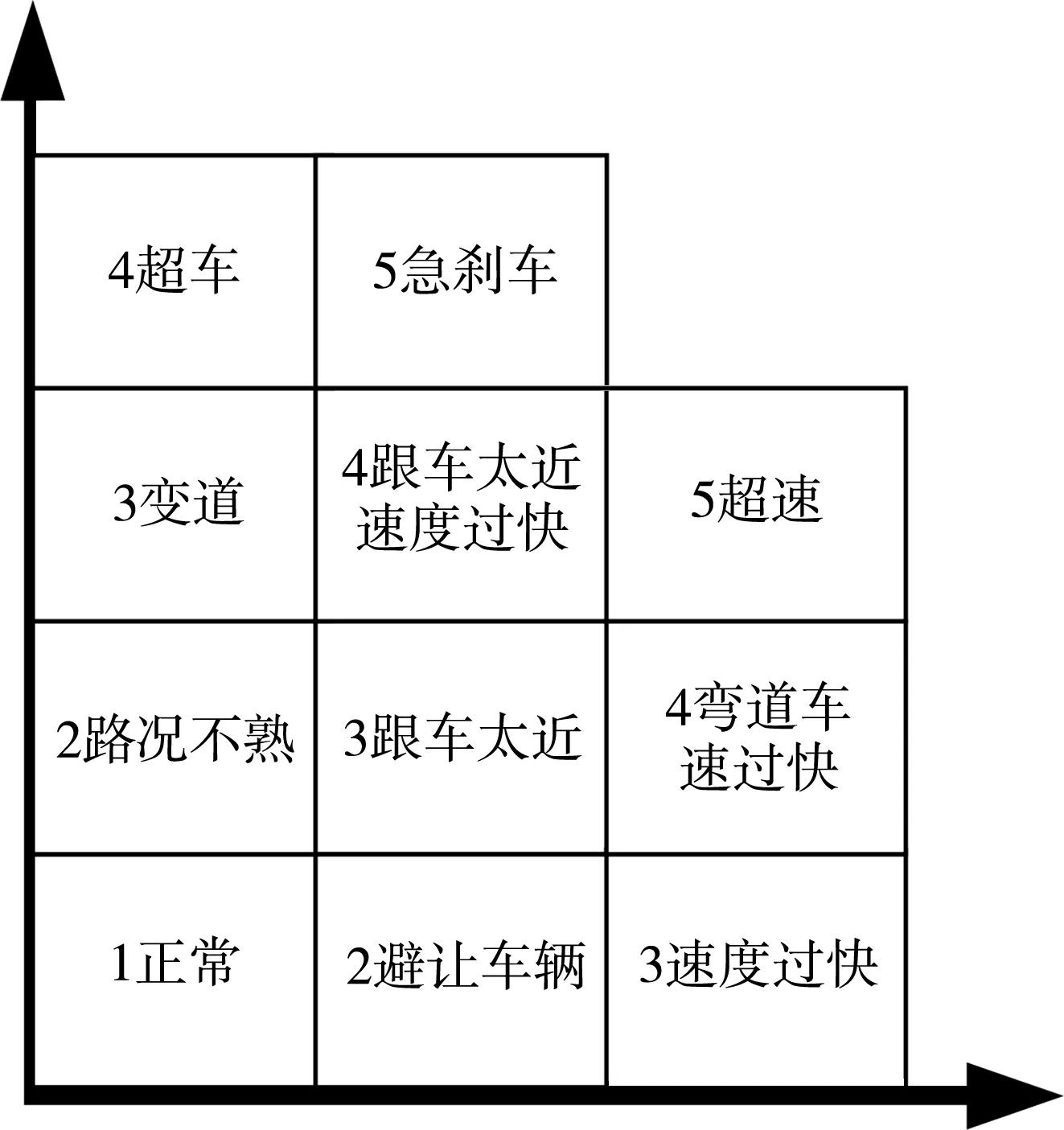
图4 人员驾驶行为

表6 变量表

2 结构方程模型

2.1 模型建立

结构方程模型由联系观察变量和潜变量的测量模型和将潜变量联系在一起的结构模型组成。根据概念研究绘制初始模型路径图，如图5所示。本文基于AMOSE(Analysis of Moment Structures)软件平台对概念模型进行分析。观察变量残差值用来表示可能出现残差间不独立或残差为负值的情况，出现负值残差将参数设定改为0.0005[13]，对于残差不独立，可通过拉相关或将相关性高的残差删除。

图5 概念模型路径图

2.2 模型修正

结构方程模型由检验测量模型是否正确的验证性因素分析(Confirmatory factor analysis，CFA)和分析各个构面之间关系的结构模型组成。

为保证结构方程模型数据的准确性，必须检验观察变量与对应的潜变量之间的关系是否正确。非标准化的估计值为自变量改变一个单位因变量改变多少个单位；标准化的估计值为自变量改变一个标准差，因变量改变多少个标准差(研究自变量对因变量重要程度)，取值为-1～1。测量模型中标准化因素负荷量(factoring loading，权重值)介于0.7至0.95为ideal，大于0.6为acceptable(探索式因素取0.3～0.5)。SMC(squared multiple correlations)为标准化因素负荷量的平方，也称题目信度(item reliability),表示潜在变数对该题目的可接受能力，大于0.36为acceptable(探索式模型取0.1～0.3)，大于0.5为ideal，在结构方程模型中SMC表示自变量对构面(潜变量)的解释能力，大于0.18为small，大于0.33为middle，大于0.67为large，在路径分析中，该值往往会被低估且模型为探索式结构方程模型，取值可适当降低。估计方法为最大似然估计。

验证性因素分析由收敛效度与组成信度构成。收敛效度AVE(取值在0.3～0.5或0.5以上)表示构面的收敛效度；组成信度CR(0.5，0.7)表示构面的内部一致性，如公式(1)和(2)所示。

(1)

(2)

2.3 模型检验

本文对结构方程模型中各种配适度指标的选取有自由度(df)、P-value、GFI、AGFI、CFI、RMSEA[14]。GFI、AGFI、CFI检验模型期望共变异数矩阵与样本共变异数矩阵的相似性，0.8以上为acceptable，0.9以上为ideal；RMSEA为两矩阵的相异性检验，小于0.08为acceptable，小于0.05为ideal[15-16]。卡方值不能过大，但同时又受到样本数的影响且与自由度成正相关，所以通过检查的值来确定，小于3表示模型可接受，小于2表示模型较好。

3 模型检验

3.1 收敛效度检验

图6-9为各测量模型数值。根据图6-9对相关性较小的因素进行筛除。环境中en1,en3,en4,en6的factoring loading 与squared multiple correlations较为理想，符合要求。危险货物中dan1,dan3符合要求(在事故中，危险货物数量对于事故影响相比货物种类和货物状态来说较小)。设施中fa1至fa4都较为理想，保留。管理中ma1～ma3都符合显著性检验，保留。

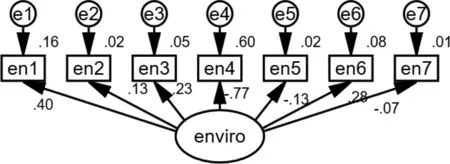
图6 环境测量模型

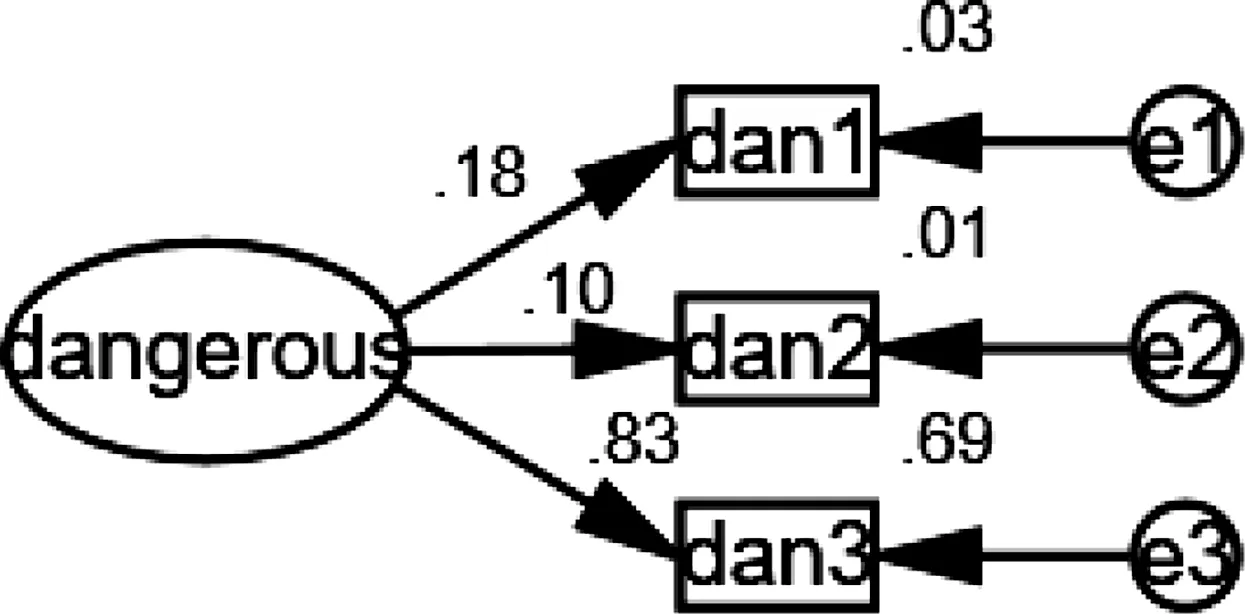
图7 危险货物测量模型

图8 设施测量模型

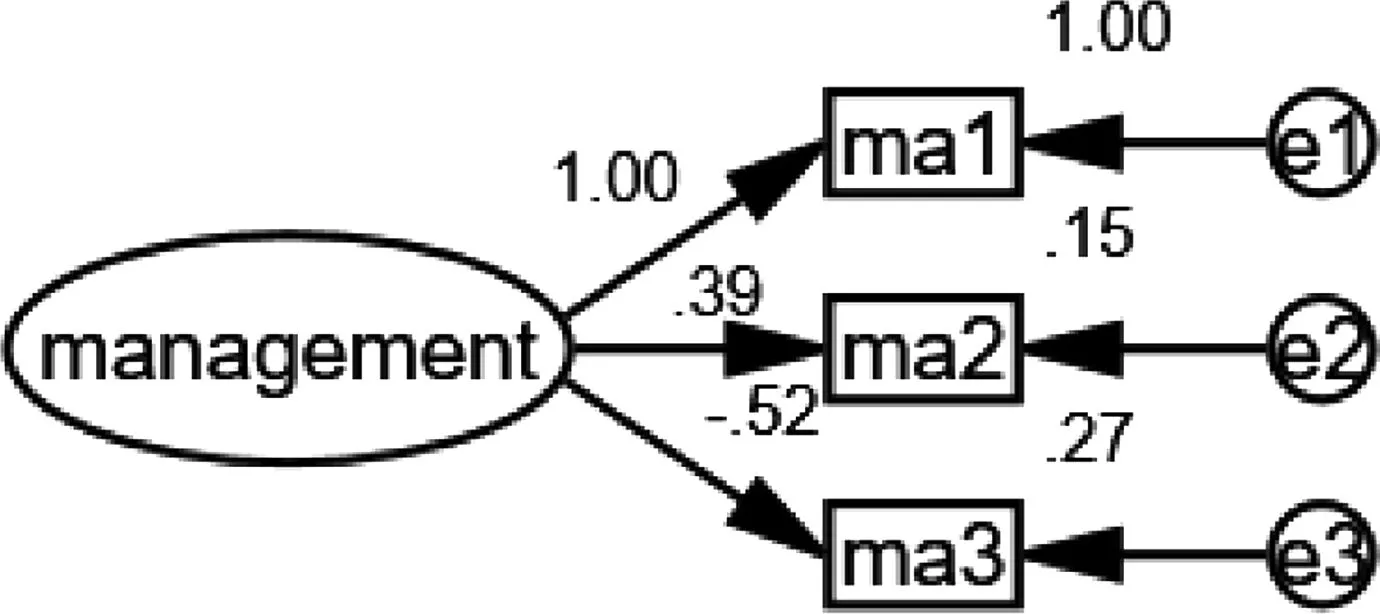
图9 管理测量模型

表7为测量模型因素负荷量表。由表7可知，除危险货物dan3以外，非标准化估计值参数显著(小于0.05)，表明参数有意义，因素负荷量多数介于0.3～0.5之间 ，题目信度多数在0.1以上，表明具有可接受的题目信度，组成信度除环境外都在0.5以上，代表内部一致性成立，除环境以外AVE都介于0.3～0.5或大于0.5，说明构面间的效度较好。

将标准化因素负荷量小于0.2的移除后，部分观察变量的标准化因素负荷量偏小，这与数据的缺失和本文探索性因素有关。在数据分析中，不能完全排除主观因素的影响，造成数据缺乏一定的信度或部分观察变数可制定到其他构面。部分标准化因素负荷量(ma1)超过1或在0.95以上(1.04～1.4之间，甚至有时超过2.80)，不代表该题目是错误的，可能是变数之间有较高的相关性(共线性)。部分残差的不独立导致个别模型配适度指标未能符合CR和AVE。因素负荷量出现负值是因为数据中存在反向题目，对结果没有影响。

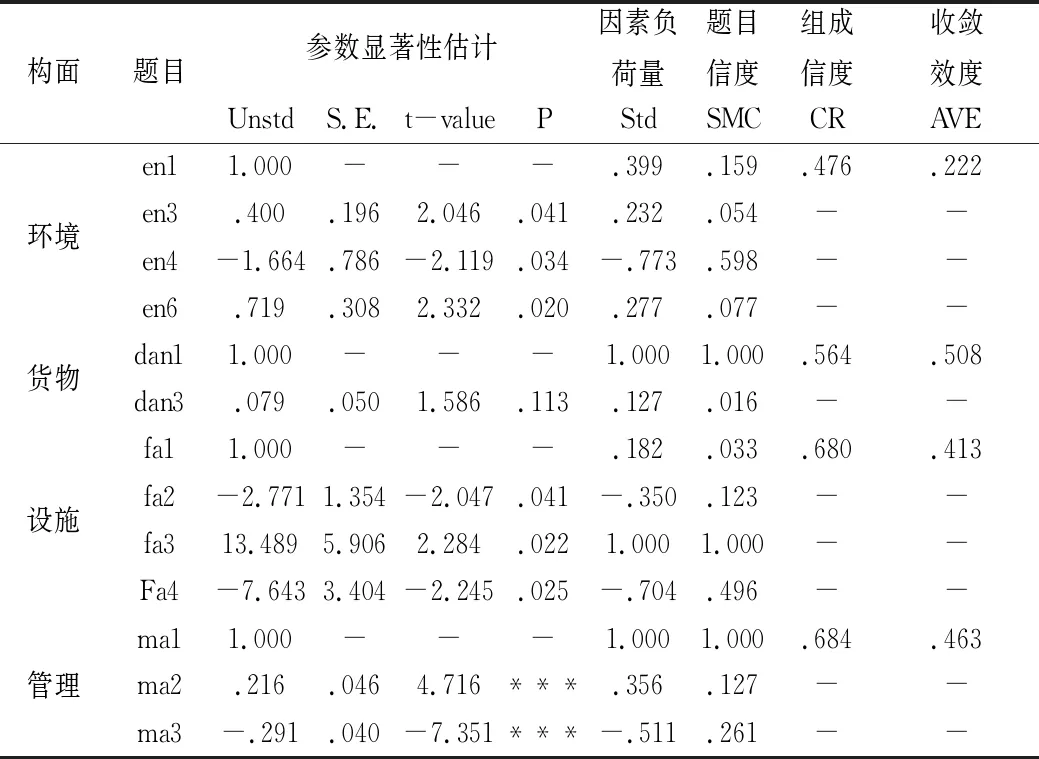
表7 测量模型因素负荷量

3.2 区别效度分析

根据测量模型绘制新的结果模型如图10所示。初始配适度指标中RMSEA小于0.08，CFI、AGFI略小于0.9，对事故的解释能力为73%。对模型修正数据如表8所示。在第三步与第四步修正中，虽然配适度指标都逐渐满足要求，但对事故的解释能力开始下降，故采用修正至第三次的结果，如图11所示。最终，各因素综合效应如表9所示，各构面间的解释能力如表10所示。

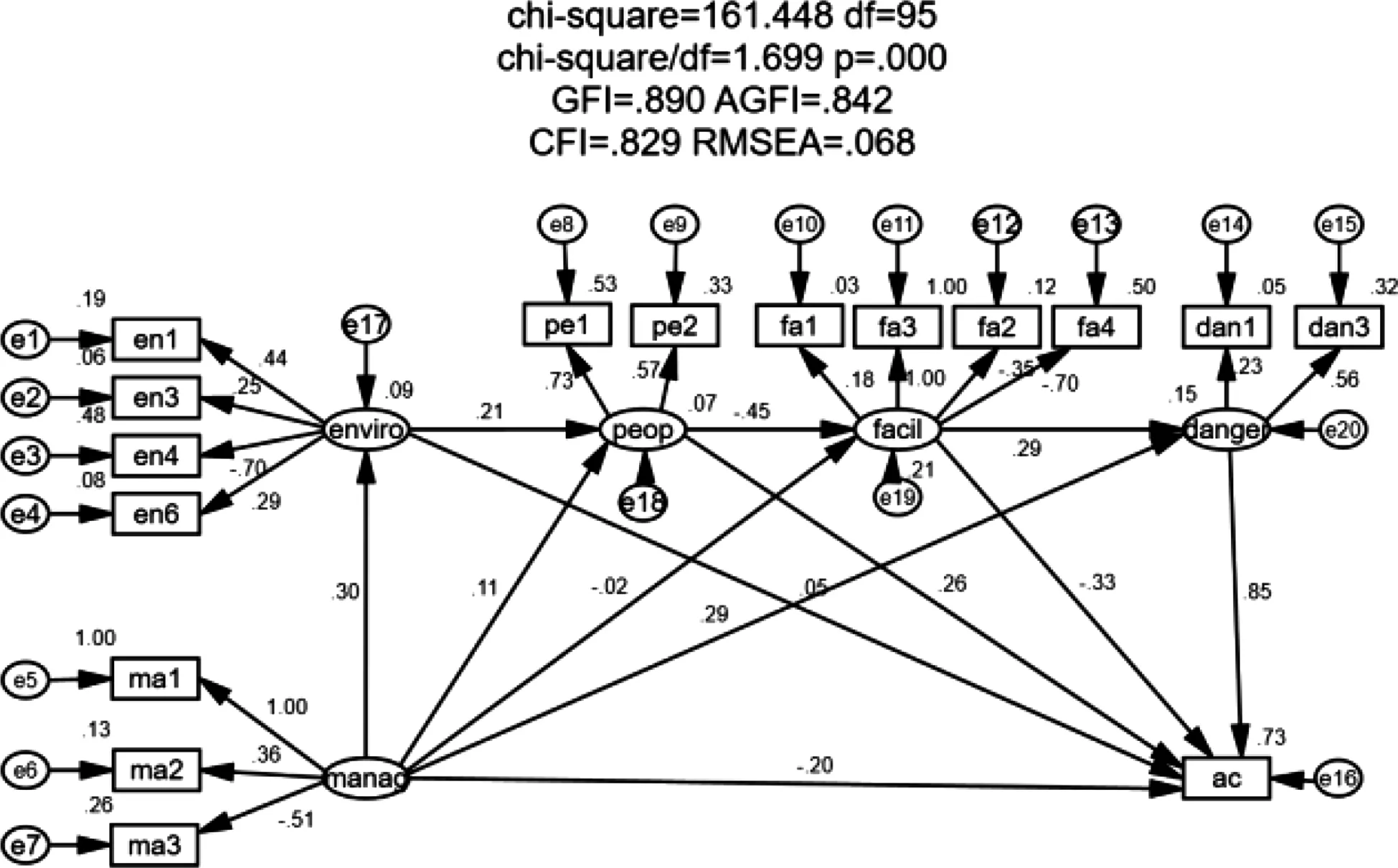
图10 结构方程模型

图11 修正后的结构方程模型

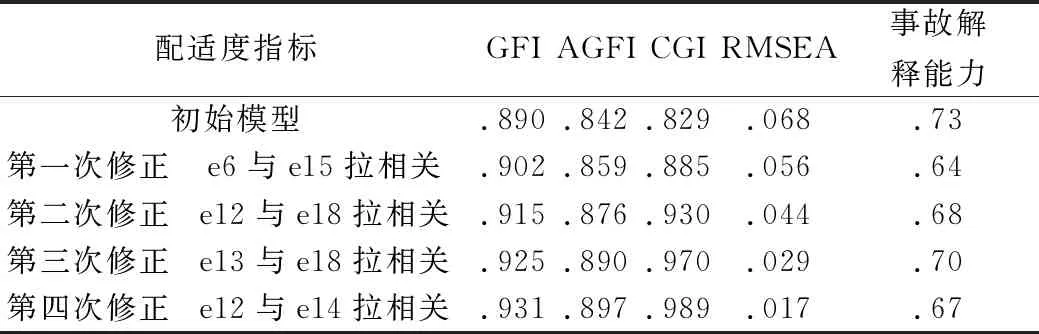
表8 模型修正

表9 影响因素综合效应

表10 构面解释能力

4 结论

由表9可知，较高影响因素中：危险货物dan3对于事故的影响程度最高(0.4648)，其次为车辆的状态fa3(-0.35)，说明随着设施使用时间的增加，其对于事故的影响在降低，较新设备反而对事故的影响较大。中度影响因素中：危险货物种类dan1对事故的影响达到0.2158，人员资质Pe1(0.213)和ma1处理时间(-0.2)次之，故障方式fa4(0.196)和pe2(0.177)、ma3(0.102)最低,其中处理时间为负值表示危险品处理时间越久，危险品泄露爆炸对周围的影响越小。

危险品、货物和人对于事故影响较高，这是因为事故的定义涉及到人车物的损耗，从表10中可以看出人对于设施的影响达到44%，而管理对于设施的影响只有2%。在事故分析过程中，因为人员操作不当导致事故的发生达到了54%，受外部环境车辆影响为38.6%。在表10中环境对于人的影响达到了23%。所以除了人员对于设施的影响，环境通过影响人从而影响人对于设施的操作导致事故发生的概率也较高。

根据表10可知，对事故、危险品、设施的解释能力分别达到70%、18%、20%，因环境与人员受事故实时数据获取的影响较大，所以对于人和环境的解释程度不到19%。环境对于人的影响为23%，人对于设施的影响为44%，驾驶行为危险等级越高，对事故的影响越大。设施对于危险品的影响为34%，而管理对于危险品的影响为29%，在数据分析过程中发现，还是存在很多因管理缺失出现的违章运输，车检货检不合格的情况。各构面对于事故的直接影响规律与表9影响因素综合效率规律相符。虽然环境对于事故的直接影响最低，但环境可通过影响人、设施和危险品从而影响事故的发生，如在事故分析中出现的因高温导致爆炸事件1次，道路标志标线不合格使驾驶人员错误判断道路情况1件。

本文虽然对重要影响因素进行了判断，得到一级影响因素为：dan3，fa3，二级影响因素为：dan1，pe1，ma1，fa4，pe2，ma3，三级影响因素为：ma2，fa1，fa2，en4，en1，en6，en3，但事故发生是突发事件，且数据多是通过事后分析获取，另外在管理方面的数据处理中(ma3)还是存在一定的主观判断，所以未来研究会基于在已有数据分析的基础上建立实时动态预警模型，通过大数据分析，不断更新各影响因素的重要程度，构建区域性动态风险等级，为事故预警提供理论支持。