基于两种机器学习方法的广西后汛期降水预测模型

覃卫坚，何莉阳，蔡悦幸

（广西壮族自治区气候中心，南宁 530022）

引言

汛期气候预测为各级政府防灾减灾决策部署工作提供了技术支撑，是每年气象部门气候预测服务重中之重的工作任务。气候变暖背景下极端异常降水事件频发，进一步加大了旱涝预测的难度，因此开展汛期气候预测方法的研究具有重要的科学意义和应用价值。目前我国短期气候预测的科技水平和业务能力已从传统的统计分析发展到了动力-统计相结合的预测技术和方法，发展动力-统计相结合的气候预测方法是现阶段及未来很长时期内提高气候预测准确率的重要途径［1-4］。国家气候中心第二代季节预测模式系统（BCC＿CSM1.1）预测能力较第一代得到了很大的提高，对大尺度环流预报能力较高［5-6］，对华南地区夏季降水量预测能力偏弱［7-8］。如何利用更有效的气候模式预测信息，就这个问题统计降尺度方法在气候预测中得到了应用，对气候模式具有较高预测技巧的大尺度环流信息和局地气象要素进行相关统计，建立预测模型，从而提高了气候预测能力［9-10］，如顾伟宗等［11］分别计算了预报对象和模式资料的预报因子场以及再分析资料的预报因子场的相关系数，利用最优回归方法建立预测模型，降水预测效果远高于模式直接输出的预测结果；封国林等［12］利用气候模式回报资料筛选出能反映模式预报误差分布特征的关键预报因子，通过计算检验得到最优多因子配置，建立汛期降水集成预测模型，提高了降水预测能力；郭渠等［13］利用BCC＿CSM 模式环流预测资料，建立多元回归预报模型，提高了夏季降水的预报技巧。以上统计降尺度方法主要使用传统的回归方法和集成建模预测，而把粒子群-神经网络和随机森林算法等机器学习方法应用其中还不多见。粒子群-神经网络等机器学习方法具有较强的处理非线性问题的能力，在气象预报中有了很好的应用效果，如陆虹等［14］、覃卫坚等［15-16］、孔庆燕等［17］、吴建生等［18］、田心如等［19］把粒子群-神经网络方法应用在广西冷湿天气、寒露风日数、降水量、夏季空调负荷预报中，预报准确度较线性回归方法有明显提高；Kim H L 和Kim B H［20］把随机森林方法应用于城市洪水灾害等级预测中，预测准确率得到了提高。因此，利用BCC＿CSM1.1 气候模式回算资料，对广西后汛期降水距平百分率进行EOF 分解，分别计算各模态时间系数和气候模式预测回算资料、气候模式回算资料和再分析资料的相关，得到高相关区域，使用逐步回归方法计算筛选得到预报因子，利用粒子群-神经网络和随机森林算法进行建模预测，为提高后汛期降水预测率提供新的思路。

1 资料和方法

1.1 资料来源

资料包括：（1）1991—2021 年后汛期（7—9 月）广西90 个地面气象观测站逐月降水距平百分率资料；（2）1991—2015 年NCEP／NCAR 2.5°×2.5°格 点月再分析资料，包括高度场、风场等；（3）1991—2021年BCC＿CSM1.1 气候模式6 月起报7—9 月逐月回报数据，包括高度场、风场、降水距平值等。BCC＿CSM1.1气候模式是第二代季节气候预测模式系统，为一个包含海陆冰气系统、植被和碳循环的全耦合气候系统模式，模式分辨率为2.5°×2.5°。

1.2 气候预测评分方法

Ps 评分计算公式：

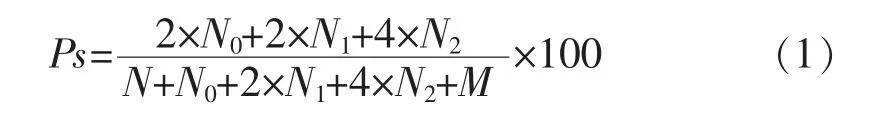
其中：N0为气候趋势预测正确的站数，N1为一级异常预测正确的站数，N2为二级异常预测正确的站数，M 为没有预报二级异常而实况出现降水距平百分率≥100%或等于-100%的站数（称漏报站）。20%≤降水距平百分率绝对值＜50%为一级异常，降水距平百分率绝对值≥50%为二级异常。

同号率指各站降水距平值实况和预报正负符号相同的站数占总站数的百分比。

1.3 粒子群－神经网络方法

Kennedy J and Eberhart R［21］1995 年提出了粒子群算法，粒子群-神经网络最优解的数学函数［17］：

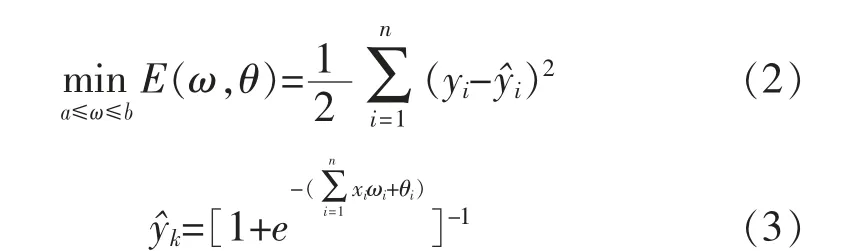
（2）-（3）式中，ω 为网络权值，n 为样本数，θ 为网络阀值，xi为训练样本的输入，θ 实际输出，yi期望输出。粒子的位置更新调整公式［22］：

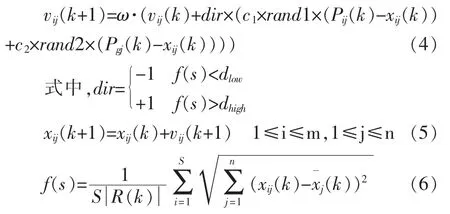
（6）式中，f（s）为种群多样性指数，S 为种群中粒子总数，，n为维数。为粒子第j 维的平均值。

当f（s）＜dlow时，dir＝-1，种群远离最优位置；当f（s）＞dhigh时，dir＝1，种群向整体最优位置靠拢。具体计算步骤［23］如下：

（1）初始化粒子群；

（2）计算每个粒子的适应度；

（3）随机输入个体最佳初始值及全局最佳初始值，再根据粒子的适应度进行更新；

（4）使用权重系数矩阵控制着网络权值和阀值的大小；

（5）连接结构矩阵变量矩阵控制着隐节点数，计算更新位置矩阵中的连接结构矩阵。

（6）反复进行（2）-（5）步骤的计算，当迭代次数达到了最大训练次数或满足最小训练误差时，停止计算，并输出最优解。

1.4 随机森林算法

Breiman［24］2001 年提出基于bagging 思想的随机森林算法，是一种使用多棵决策树对样本进行训练和预测的分类器，它由不完全相同的单棵决策树组成，利用多棵决策树投票机制来决定最终的分类［25］。随机森林算法具有分类速度快、可调节参数少、计算效率高、减少过拟合现象等特征。设定含有N 个样本的原始样本集，从原始样本集中随机抽样，组成多个训练集，建立N 棵决策树［26］：

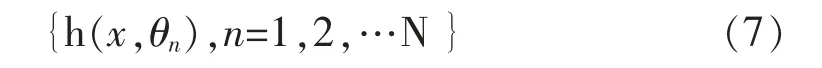
x 为输入的自变量和因变量，θn为服从独立同分布随机向量。

在训练决策树模型的节点时，随机从节点上所有样本特征中选择一部分样本特征，以其中最优的一个特征来划分决策树的左右子树，训练结束后进行投票得到所有模态的平均值作为输出：

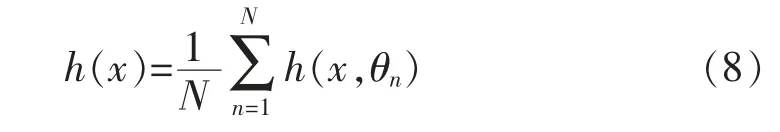
2 因子选取

2.1 EOF 分解

对1991—2015 年广西90 站后汛期降水距平百分率进行EOF 分解，得到主要空间模态和各模态的时间系数。各特征向量能够反映出后汛期降水变化的空间结构，第一模态是后汛期降水变化最具有代表性的分布场，其次为第二模态、第三模态等，前三个模态的方差贡献率分别为51.4%、13.7%、7.2%，前三个模态累计方差贡献率达到了72.3%，第四个模态方差贡献率仅为4.1%，相对前三个模态方差较小，为了减少计算量，只计算前三个模态的时间系数。第一模态特征向量值基本为正值（图1a），体现了广西后汛降水的一致性变化这一重要特征。第二模态特征向量值呈桂北为正值、桂南为负值的空间分布特征（图1b），说明了桂南和桂北降水存在反相的变化特征。第三模态特征向量值桂西为正值、桂东为负值的空间分布特征（图1c），即桂西和桂东降水存在反相变化特征。从各模态时间系数历年变化来看，第一时间系数（PC1）1990—2010 年呈现出减小趋势，2011 年以后为增大趋势；第二时间系数（PC2）为减小趋势，其中1991—2003 年变化幅度比较大，2003 年之后变化趋于平缓；第三时间系数（PC3）1991—2000、2010—2015年变化比较平缓，2000—2010 年变化幅度大（图1d）。

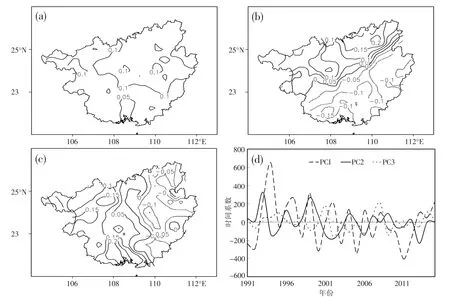
图1 广西后汛期降水EOF 前三个模态空间分布及时间系数

2.2 预测因子的查找和筛选

因子查找从两个方面入手：一方面，计算后汛期降水距平百分率的前三个模态时间系数与BCC＿CSM1.1模式6 月起报的环流预测资料的相关系数，得到显著相关的区域；另一方面，计算BCC＿CSM1.1 模式环流预测和NCEP／NCAR 实况场的相关系数，得到模式环流预测的高技巧区，即相关系数通过水平为0.05 的显著性检验区域。选出各模态时间系数与模式预测资料的相关显著区域，同时这区域也是模式预测高技巧区，把区域格点值进行平均后作为预选因子。为了保证在已选定的一批因子中得到最优的因子，使用逐步回归方法再进一步筛选，建立第一模态时间系数逐步回归预报方程：

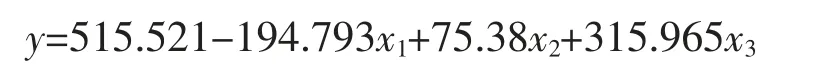
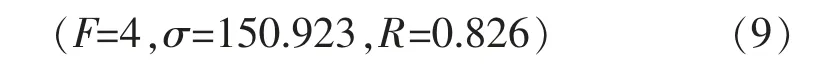
式（9）中，x1、x2、x3分别为巴尔喀什湖和贝加尔湖之间区域、秘鲁西海岸附近、南非的200hPa 经向风，如图2a 所示。

第二模态时间系数逐步回归预报方程：

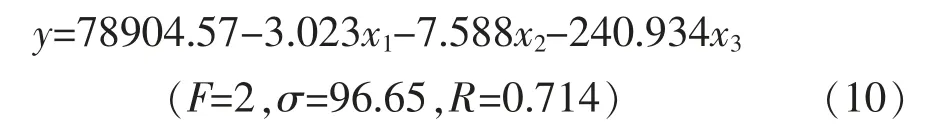
式（10）中，x1为南非以南地区200hPa 高度场，如图2b 所示；x2、x3分别为巴尔喀什湖以南附近地区、美国和墨西哥交界地区500hPa 高度场，如图2c 所示。

第三模态时间系数逐步回归预报方程：

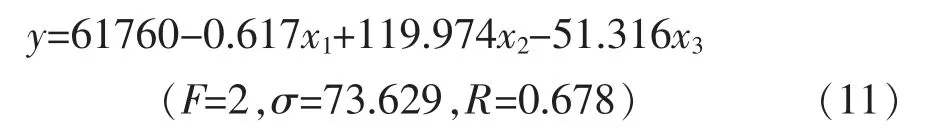
式（11）中，x1为贝加尔湖东部地区海平面气压，如图2d 所示；x2为澳大利亚南部850hPa 纬向风，如图2e 所示；x3为南美洲西部沿海200hPa 经向风，如图2f 所示。式（9）—式（11）σ 表示剩余标准差，R 表示复相关系数。

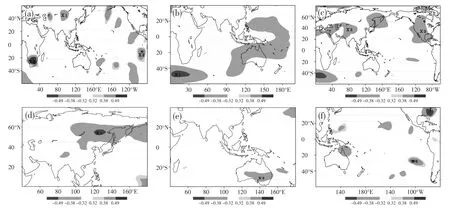
图2 1991—2015 年第一模态时间系数与模式200hPa 经向风的相关（a），第二模态时间系数与模式200hPa 高度场（b）、500hPa 高度场（c）的相关，第三模态时间系数与模式海平面气压（d）、850hPa 纬向风（e）和200hPa 经向风（f）预测值的相关分析（阴影为通过0.1 显著性水平检验的区域）

3 预测结果对比分析

通过逐步回归方程筛选得到预测因子，使用粒子群-神经网络和随机森林算法建立预报模型。粒子群-神经网络预报模型输出节点个数为1，隐节点下限为0.3，隐节点上限为1.5，目标误差为0.01，学习速率为0.5，动量因子为0.75，训练次数为200，个体最优导向系数为2，全局最优导向系数为2，粒子位置下限为-3，粒子位置上限为3，种群规模为50，最大迭代次数为100。随机森林算法策略树的数量为50，构建决策树时对于节点数量没有限制，没有限制计算量，利用最大资源建模直至得到最优解。

利用粒子群-神经网络、随机森林算法、逐步回归方法对三个模态时间系数进行预测，得到2016—2021 年各模态时间系数预报值，再与对应的特征向量相乘，最后合成得到降水距平百分率的预报场。表1 给出了2016—2021 年粒子群-神经网络、随机森林算法、逐步回归方法和气候模式的后汛期降水预测Ps 得分和同号率，两种机器学习方法预测得分均高于逐步回归方法和气候模式，其中粒子群-神经网络方法平均得分最高，为81.53，较逐步回归方法和气候模式分别提高了2.78、29.22；其次为随机森林算法，平均得分为81.25，较逐步回归方法和气候模式提高了2.5、28.94；两种机器学习方法预测和实况同号率比逐步回归方法提高了0.04、比气候模式预测提高了0.31。从6a 的预测试验来看，2017 和2021 年气候模式预测误差较大，2017 年广西降水实况为偏多，而模式预测降水偏少；2021 年气候模式预测广西降水偏多，而实况是偏少。可见，利用模式有效的环流预测信息来建模预测，能够明显的提高降水的预测能力。

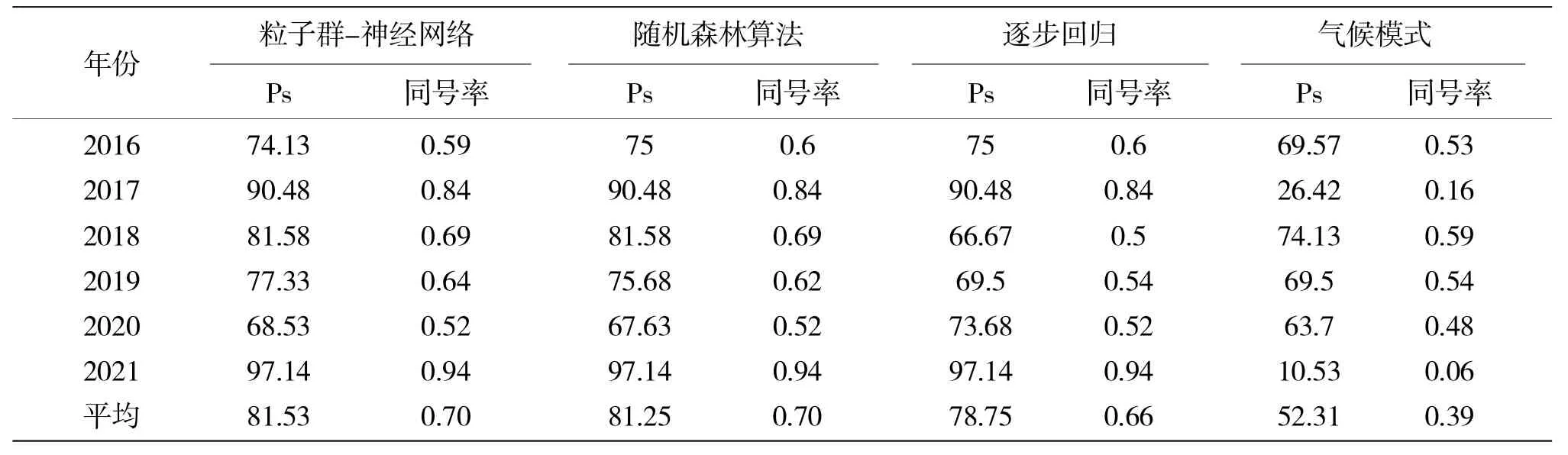
表1 粒子群－神经网络、随机森林算法、逐步回归方法、气候模式后汛期降水预测Ps 得分和同号率

4 结论和讨论

利用BCC＿CSM1.1 气候模式预测等资料，使用相关方法查找和筛选得到预测因子，建立基于粒子群-神经网络、随机森林算法的广西后汛期降水气候预测模型。在2016—2021 年业务预测试验应用中，基于粒子群-神经网络、随机森林算法的后汛期降水预测Ps 得分较逐步回归方法分别提高了2.78分、2.5 分，较气候模式分别提高了29.22 分、28.94分，预测能力有明显的提升。

本文利用粒子群-神经网络、随机森林算法机器学习方法对气候模式降水进行订正，做了初步的预测试验，取得了良好的预测效果。这得益于本研究充分利用了气候模式有效的预测信息，在建模预测中机器学习算法具有自学习能力，较传统线性统计方法对复杂的非线性模型能够更准确的描述。在后续的研究中，将增加更多气候模式资料，做进一步的试验和研究。