基于Φ-OTDR 系统事件的快速定位方法

孟金昌

（武汉邮电科学研究院，湖北 武汉 430000）

近年来，相敏光时域反射仪（Φ-OTDR）因其具有完全分布式振动传感器的能力而备受关注[1-3]。Φ-OTDR 系统通常将高度相干的探测器光脉冲发射到传感光纤中，并接收后向散射光，以通过相干检测技术监视沿传感光纤的外部振动干扰[4-6]。与传统的OTDR 不同，传统的OTDR 仅监视沿光纤的背向散射光的变化，而Φ-OTDR 系统可检测背向散射光的相位变化[7-8]。通过提取相位变化，可以利用Φ-OTDR技术提供外部振动源类型的信息。因此，基于ΦOTDR的分布式传感器有望实现广泛的应用，如沿油气管道的异常振动检测、入侵报警和定位系统以及用于火车跟踪的分布式声学测试[9-12]。

为了在Φ-OTDR 系统中沿着传感光纤精确定位外部振动，已经提出并探索了基于幅度的定位技术和基于相位的定位技术，包括移动平均、小波变换、二维双边滤波算法、微分相位方法等[13-15]。基于幅度的定位技术，主要优点是可以通过平均方法来抑制信号衰落引起的定位错误警报[16]。然而，大多数基于幅度的定位方法都需要相对复杂的算法来逐点处理所有获取的感测数据[6-7]计算成本高。对于基于相位的定位技术，其优点是用于定位外部振动的信噪比（SNR）相对较高，可以达到10 dB。然而，由于信号衰落，Φ-OTDR 系统中不可避免地存在大量的虚警相位峰值，这导致了辨别此类虚警相位峰值的大量计算成本。

文中提出了一种快速定位方法，以提高ΦOTDR 系统定位外部振动事件的效率。由于外部振动会在振动区域之外感应出一个附加相位，而信号衰落对其位置之外的相位影响很小，因此可以先将背向散射的数据分为几个相距很远的段，进行预处理。沿光纤的与外部振动无关的批次传感点被排除在外。其次，使用相位解调进行定位，在包含外部振动的目标段内实现精准定位。由于大多数无关且提供冗余信息的传感点都被丢弃，该方法能显着降低信号处理负荷，尤其是对于长距离传感光纤。此外，结果表明计算成本对感测范围不敏感。

1 Φ-OTDR系统相位解调原理

在使用相干探测的Φ-OTDR 中，IQ 解调因其简单并容易应用的原理而被广泛应用，具体的解调算法流程图如图1 所示。

图1 IQ解调算法流程图

IQ 解调主要有混频、滤波、解调3 部分。假设原始信号的形式如式（1）所示：

其中，A指信号幅值，φ(t)指干扰信号的相位，ω为AOM 引入的调制频率。

首先对采集到的原始信号进行混频，一路信号是同相信号I，另一路是与之正交的信号Q，S(t)分别与正弦和余弦函数相乘以后便可以得到φ(t)的分量，以及使用AOM 调制的光频ω的二倍频分量，I、Q可以用式（2）和式（3）表示：

利用低通滤波器消除其中的倍频分量，这使得滤波后的信号只保留了外界振动事件的φ(t)信息，得到的相互正交的信号进行反正切运算，即可初步得到振动事件的相位，如式（4）所示：

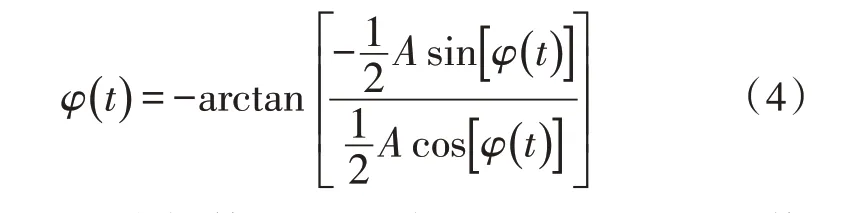
再经过解缠绕算法对相位中的突变点进行修正，即可将其真实相位解调出来。

2 Φ-OTDR系统快速定位原理

定位方法中仍然采用传统Φ-OTDR 光纤传感系统，方法流程如图2 所示。

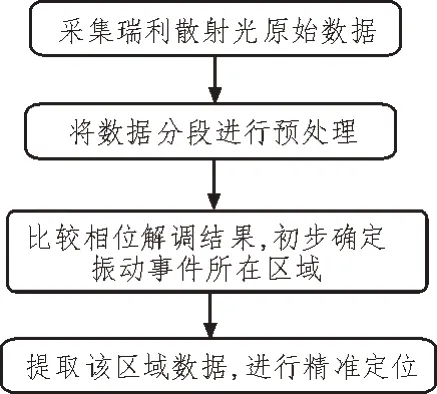
图2 快速定位方法流程

首先，构建信号的数据矩阵，在采集数据时构建数字信号矩阵A=[Ai,j]，其中Ai,j表示Φ-OTDR 传感系统的数据采集卡采集到的信息，具体来说，指的是第i个光脉冲到达传感光纤第j个数据点时的瑞利散射光的数字信号值，矩阵的行向量是单个光脉冲对应的数字信号，在Φ-OTDR 系统中，传感光被调制为多个连续的光脉冲信号，按发射的时间顺序依次将其对应的数字信号作为第1 行、第2 行……第M行，这里M代表了光脉冲个数，矩阵的列向量N代表了单个脉冲采集到的信号数据长度。

其次，在数字信号矩阵A上每隔一定光纤传感长度L取一次测试窗口WK，确保测试窗口WK的宽度l远小于L；结合相位解调算法解调这一测试窗口WK的相位信息，将其中某一列的相位数据作为测试列相位φk，其位置用jk表示；对每条测试列相位进行相位解卷绕，把相位变化拓展到整个实数范围。

再次，定位扰动区间的粗略位置，具体操作方法是按顺序比较所述相邻测试列相位，若相邻列相位φk和φk+1相等，即φk=φk+1，则可以判定区间(jk，jk+1)无扰动；若相邻测试窗口测试列相位φk和φk+1不相等，即φk≠φk+1，那么判定该区间(jk,jk+1)存在扰动。

最后，精确定位扰动位置，当系统判定某区间(jk,jk+1)存在扰动时，对该区间范围内的所有光数字信号进行相位解调，结合前文所述的差分补偿算法对扰动信号进行精确的定位和还原。

3 实验结果及分析

3.1 实验测试结果

为了模拟外部振动源，在传感光纤的2.58 km 处施加由80 Hz 正弦电压信号驱动的压电换能器（PZT），在传感光纤某一位置处使用函数发生器产生正弦信号来模拟外界振动事件。

当所述的传感光纤上的某一点受到振动信号的干扰时，由光的弹光效应可知，光脉冲在经过该扰动点时将引入一个附加相移∆φ，且附加相移量受外界扰动调制。光脉冲将携带该附加相移∆φ继续在光纤中传播，传播过程中产生相位和光脉冲相位相同的瑞利散射光，因此，在扰动点后所产生的瑞利散射光经过扰动点时相位均将再附加∆φ，且该附加相移仅由扰动造成，信号衰落噪声和无扰动的情况则不会引入该附加相移。基于这一原理，仅仅根据相邻测试窗口中对应的测试列相位的相似程度以及这两个测试列相位发生的能量变化即可确定该区段是否发生了扰动，即若相邻测试窗口之间无扰动，两测试列相位相同；若相邻测试窗口之间存在扰动，两测试列相位不同。

为了识别粗略定位的观测点之间的相位差，采用自相关算法的判据。皮尔逊相关系数r通常用于测量离散随机信号的线性关系，表示为式（5）：

其中，X和Y表示要比较的随机信号，-X和-Y分别表示X和Y的期望，k表示离散信号中的值的索引号。由于r的范围为[-1，1]，强相关使r接近1，因此信号之间的高度相似性会导致r值较大。为了突出粗略定位过程中相邻观测点之间的相似性，将相关系数si定义为式（6）：

其中，φi表示第i个观察点的相位。如果φi与φi-1不同，则si相对较高，并且将第i段视为与振动相关的段。

首先，将整个传感光纤划分为100个间隔为100 m的段和101 个观测点，以实行粗细定位方案。注意，在实验中，需要在每个段的末尾有一个观测窗，以从指定的观测点解调相位。通过使用式（5）和（6），计算相邻观测点的相关系数，预处理后的初步定位结果如图3 所示。峰值表明外部振动发生在第25 段内，该段对应于2.4 km和2.5 km 之间的间隔。从连续端点24(2.4 km)，25(2.5 km)和26(2.6 km)提取解调后的时间相位。发现∆ϕ25和∆ϕ26 几乎相同，但与∆ϕ24 不同。同时，通过从相邻观测点中减去时间相位（∆ϕ25=ϕ25-ϕ24,∆ϕ26=ϕ26-ϕ25），获得时间相位差分布（∆ϕ）。相位差∆ϕ25 呈现与施加的PZT 振动相匹配的正弦信号，而相位差∆ϕ26趋于零。非零差异表明传感光纤在第25 段内受到干扰，相关系数中的SNR 粗略定位约为44.55 dB。SNR 计算公式如式（7）所示：

图3 预处理后的相关系数分布图

其中，As指信号的幅值，An是背景噪声的均方根。根据上述预处理过程，可以丢弃大部分无干扰的部分。

接着在目标段上进行精确定位以实现准确的振动位置，此时仅需要解调100 m的传感光纤。为了避免信号衰落引起的虚警相位峰值，采用前文所述的相位解调方法来确定振动的位置，如图4 所示，由于振动点位于2.58 km 处，故空间分辨率约为5 m。

图4 精确定位所得的相位方差

3.2 实验结果分析

进一步研究了外差相干Φ-OTDR 系统中定位信号处理的总体计算成本。计算成本取决于信号的复杂程度，是影响传感系统响应速度的主要因素。由于每个观测点都经过相同的解调，因此计算成本取决于观测点的数量。此处，用于直接定位（一个接一个地处理每个观测点）的计算成本Cd可以表示为式（8）：

其中，q表示每单位长度的观测点数量，L表示整个感应范围的长度。所提出的由粗到细的定位方法的计算成本Cr-f可用式（9）来表达：

其中，Lseg表示用于粗定位的片段的长度，n表示目标片段的数量。运算符表示舍入运算，w表示每个片段的观察窗长度。在该实验中，q为2.5 个/m，DAQ 采样率为1 GS/s，Lseg为100 m。为了实现快速定位，观察窗的长度w应该尽可能小。同时，为了保证粗定位的可靠性，观察窗中包含的观测点应避免在信号衰落或振动位置选择观察点。在这里，w被优化为20 m，覆盖50 个观测点。由于同时发生衰落的观测点数量的可能性较低，因此有可能获得一个被选作端点的观测点，该观测点在20 m的窗口内不发生衰落。而且，选择这样的观测点，使其与相邻观测点之间的相位差最小，以避免发生振动事件。

这种计算成本比直接定位的计算成本小得多。随着传感光纤长度的增加，使用粗细定位法的计算成本逐渐增加。但与直接定位过程相比，粗细定位方法相对于长度增加的感应范围不敏感，因为通过粗定位过程排除了大多数感应点，这样仅消耗了少量计算量。而且，由于所提出的粗细定位方法是基于软件算法而非硬件布置的解决方案，它显示了与众多相干Φ-OTDR的兼容性，因此，它也适用于模拟外差解调方案和基于FPGA的实时定位方案，以进一步降低远程Φ-OTDR 系统的总计算成本。

预处理定位的SNR 随分段长度的增加而降低。由于激光源引起的相位噪声会随着距离的增加而累积，因此长度不能太大。应通过考虑实际应用中所需的响应速度和稳定性来优化段长度。此外，应该讨论所提出的粗定位方法的潜在局限性。对于因温度波动而引起的相变在整个段中变得显著的情况，公式中定义了相关系数。即使没有外部振动也显示在零以上。但是，当振动引起的峰值大于可能由于温度变化而引起的噪声背景时，仍然可以找出振动。为了使来自温度串扰的影响最小化，应根据各种实际应用来考虑优化的相关系数阈值。在粗略定位过程中还应考虑另一个问题，如果振动源作用在一个段内的传感光纤上，可能会遇到这样的情况：由于沿光纤压缩段和扩展段的大小相似，例如，两个振幅相似的振动源，后向散射光的相变被抵消了。对于这种特殊情况，粗定位过程有一定的局限性。不过，在实践中，外部振动扰动通常在振动谱中具有一定的带宽，很少同时消除由多个频率引起的相位变化。因此，提出的快速定位方法可以满足大多数实际需求。

4 结论

为了解决Φ-OTDR 光纤传感系统数据量庞大，运算困难的问题，提出了一种针对光纤传感系统的快速定位方法，解决了相干探测Φ-OTDR 光纤传感系统解调运算量大的难题，且该方法是一种软件算法，简单易行，适用性强，几乎可以直接应用在所有的相干探测Φ-OTDR 系统。

该方法摒弃了以往的逐个对传感信息点进行解调直接定位的方法，将定位过程分为两个步骤：预处理和精确定位，经过预处理后，排除了大多数无价值的观测点，但保留了一些与干扰信号直接相关的观测点，因此，可以大大降低用于定位的计算成本。系统能够实现的扰动位置粗略定位信噪比可达40 dB以上，在精确定位后，实现的空间分辨率为5 m。通过使用所述的快速定位方法，排除大量无效传感点，仅对存在扰动信息的这部分传感点进行解调和分析，极大地降低了系统的运算负担，提高了系统的实时性。所提方法可以在如火车跟踪、电网监测、分布式传感系统等实时性要求很高的场景下得到充分利用。