横观各向同性沥青路面加铺结构力学响应研究*

蒋倩灵香， 黄旺

(长沙理工大学 交通运输工程学院， 湖南 长沙 410114)

目前大多数力学试验和路面结构计算模型将沥青混合料假定为均质各向同性材料，而沥青混合料、基层和底基层材料的力学性能具有横观各向同性的性质。一般认为沥青混合料具备横观各向同性，即垂直于压实方向的水平面上2个方向的材料特性相同，而垂直方向和水平方向有显著差异。针对横观各向同性，文献[1]研究了沥青路面材料各向同性和不同横观各向同性特性条件下沥青路面三向应变场的差异，文献[2]运用横观各向同性弹性半空间地基模型分析了板的弯曲，文献[3]研究了任意荷载作用下层状各向异性弹性地基直角坐标解；文献[4]采用有限元方法对比分析了各向同性和不同横观各向同性条件下结构层间应力、应变及弯沉。基于各向同性分析路面设计可能会低估与剪应力、拉应力相关的永久变形和疲劳开裂，故在沥青路面力学响应分析时应适当考虑混合料横观各向同性。该文选取中国典型的半刚性基层沥青路面结构，以规范推荐的沥青混合料模量取值为依据建立三维有限元模型，通过改变横观各向同性系数α，分析路面结构不同控制指标的变化，为旧沥青砼路面沥青加铺结构设计提供理论参考。

1 沥青路面结构方程

假定横观各向同性体是理想的弹性结构，根据胡克定律可得出其应变-应力线性函数。横观各向同性和正交各向异性是复合材料中常见的2种类型。正交各向异性存在2个垂直面，有9个计算参数，其弹性本构方程为：

(1)

其矩阵形式为：

(2)

横观各向同性的某一平面性质一致，假定性质一致的平面是X-Y。以a、b分别表示横观各向同性中的横向和竖向，则有Ez=Eb，Ex=Ey=Ea，Gxy=Ga，Gxz=Gyz=Gb，μxz=μyz=μab，μzx=μzy=μba，其中Ga=Ea/2(1+μa)(Ga为水平剪切模量，Gb为竖向剪切模量)。故横观各向同性材料的弹性常数减少为水平向弹性模量Ea、μb和水平法向的Eb、Gb、μa5个参数，其矩阵形式为：

(3)

2 沥青路面加铺结构有限元模型

中国路面设计规范以双轮组单轴载100 kN作为标准轴载，以BZZ-100表示。荷载接触面形状为矩形时，竖向剪应力、面层剪应力及上面层层底拉应力的响应比圆形接触面时更敏感，故采用双轮荷载下矩形接触面，通过标准轴载BZZ-100换算。矩形边长为长边26.70 cm、短边13.35 cm，接地内侧边缘之间间距为10.65 cm(见图1)。

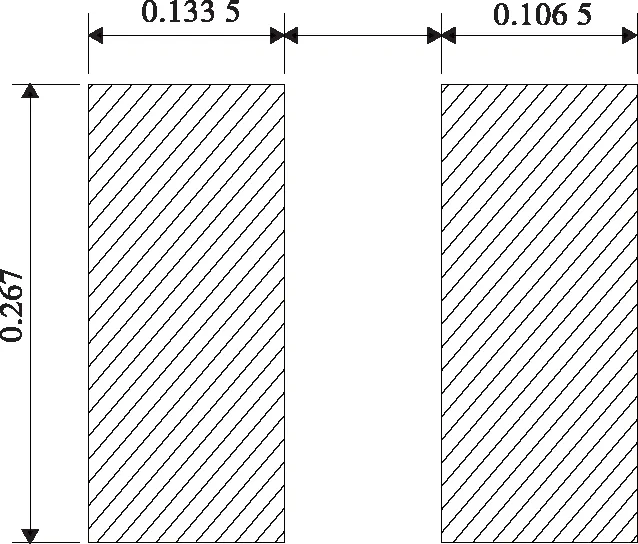
图1 荷载接触面形状(单位：m)

路面结构采用10 cm沥青加铺层+12 cm旧沥青砼层+32 cm基层及半无限体土基。在进行数值计算时，为节约计算时间，提高计算精度，路面结构模型尺寸采用4 m×4 m×4.54 m(见图2)。

图2 路面结构模型示意图(单位：m)

根据相关研究，各向异性体的垂直弹性模量比水平弹性模量大。将横观各向同性系数α(水平模量与垂直模量的比值)作为调整标准，分别设置沥青混合料弹性模量的横观各向同性系数为0.5、0.6、0.7、0.8、0.9、1，α=1表示沥青混合料材料各向同性。路面材料参数见表1、表2。

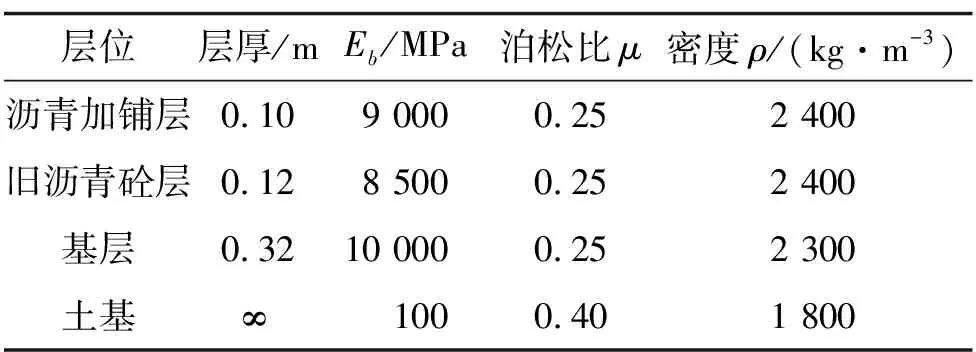
表1 各向同性路面材料参数

表2 横观各向同性路面材料参数

将垂直于行车方向的2个端面、沿行车方向的2个端面及底部设为固定约束，对车轮荷载作用区域进行局部加密以提高计算精度，对其他区域网格朝车轮荷载作用区域作加密渐变处理(见图3)。

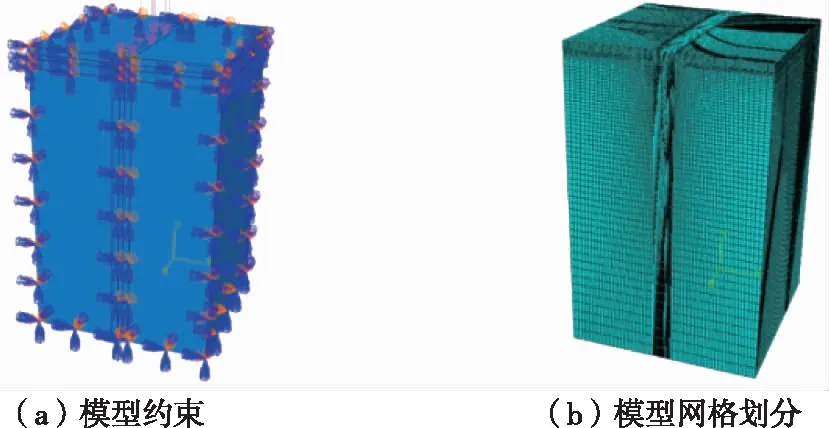
图3 结构模型约束和模型网格划分

3 静载下沥青路面力学分析

3.1 剪应力

沥青加铺层剪应力随横观各向同性系数α的变化见图4。

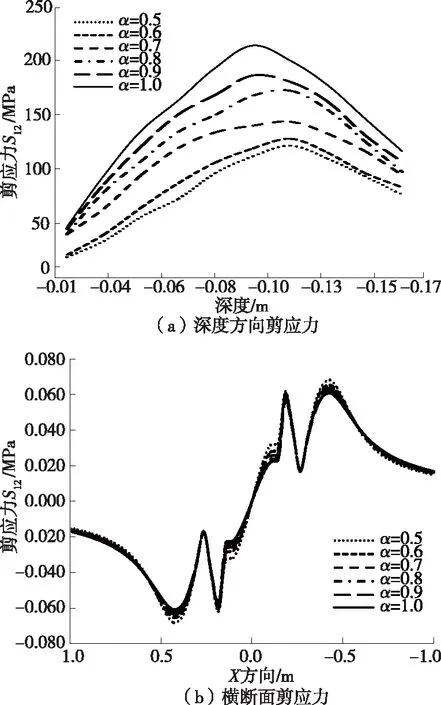
图4 不同横观各向同性系数α下沥青加铺层剪应力的变化

由图4可知：1) 不同横观各向同性系数α下，沥青加铺层剪应力随着深度的变化并不是持续增加，存在各自的峰值，但α取不同值时剪应力峰值都不在沥青加铺层中间位置(沥青加铺层厚度为0.10 m)，而是出现在其附近。α=1.0时，剪应力在深度0.09 m处出现峰值；α=0.8时，剪应力在深度0.108 m附近出现峰值；α=0.5和0.6时，剪应力在深度0.112 m附近出现峰值。随α增长，沥青加铺层中越快出现剪应力峰值点。以中心为分界点，沥青路面表面荷载位置向中心位置剪应力增长较快，中心位置往下受力慢慢趋于稳定，剪应力缓慢减小。2) 横断面剪应力曲线相对紧密，说明横观各向同性系数α对横断面剪应力的影响较小。剪应力曲线关于原点反向对称，x在(0.1，0.4)和(-0.4,-0.1)时曲线关于荷载中心反向对称。

取深度0.08 m附近最大剪应力进行横观各向同性的横向对比，结果见图5。由图5可知：随横观各向同性系数α的增长，沥青加铺层受到的剪应力减小，沥青加铺层的剪应力水平随沥青砼材料水平模量的增加而有所降低。

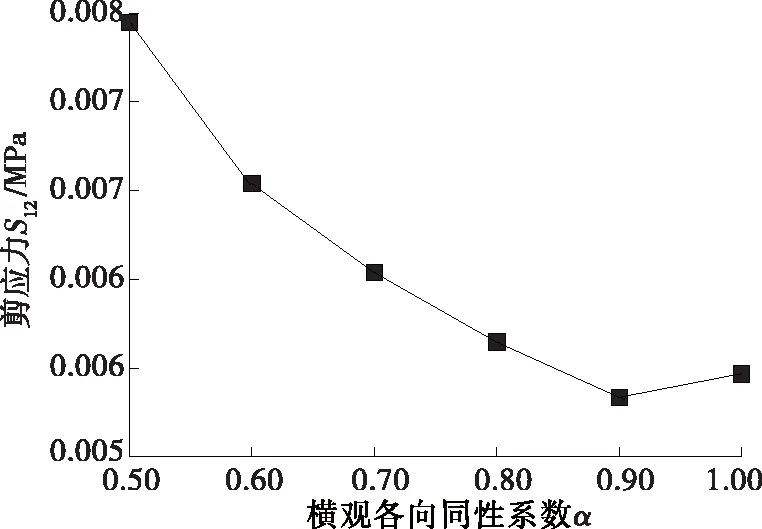
图5 沥青加铺层剪应力最大值随横观各向同性系数α的变化

3.2 沥青加铺层层底拉应力

沥青加铺层层底拉应力随横观各向同性系数α的变化见图6、图7。

图6 不同横观各向同性系数α下沥青加铺层层底拉 应力随横断面的变化

由图6可知：不同横观各向同性系数α下，随横断面的变化，双轮荷载作用下沥青加铺层层底拉应力在荷载作用位置呈现2个峰值，应力曲线在双轮荷载位置出现明显下凹。α=0.5时，应力曲线变化突出，荷载中心出现与路幅中心类似的负向峰值；α逐渐接近于1.0时，应力曲线的变化变缓；α=1.0即各向同性时，应力曲线变化圆滑，荷载作用位置不存在突变。

由图7可知：不同横观各向同性系数α从0.5增长到1.0，层底拉应力减小39.5%。而以各向同性特性进行加铺层力学分析，沥青加铺层底部最大拉应力偏小。

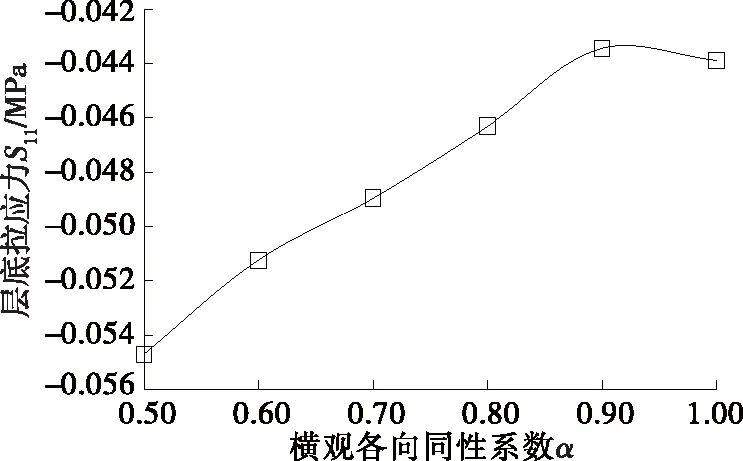
图7 沥青加铺层层底拉应力随横观各向同性 系数α的变化

3.3 土基顶部竖向压应变

土基顶部竖向压应变随横观各向同性系数α的变化见图8、图9。

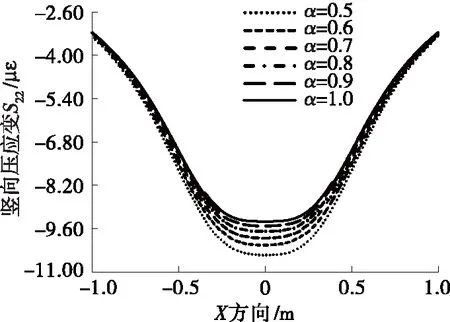
图8 不同横观各向同性系数α下土基顶部

图9 土基顶部竖向压应变随横观各向同性系数α的变化

由图8可知：不同横观各向同性系数α下，沥青加铺结构土基竖向压应变关于路幅中心位置对称，呈U状，横断面-0.5、0.5 m位置向外延伸，土基竖向压应变逐渐减小，即压应变自中心位置向两边减小；不同α下，土基顶部竖向压应变的变化趋势一致；竖向压应变随α的增大而减小。

由图9可知：随横观各向同性系数α的增大，土基竖向压应变减小。α=0.8时，S22=-9.68 με；α=0.9时，S22=-9.55 με；α=1.0时，S22=-9.4 με；α=0.5～0.6时，竖向压应变迅速减小；α=0.6～1.0时，竖向压应变变化减缓。而以各向同性特性进行加铺层力学分析，所得土基顶部竖向压应变偏小，不符合结构设计安全性要求。

4 结论

横观各向同性系数对沥青路面加铺结构的剪应力、加铺层层底拉应力和竖向压应变存在影响，前述路面结构条件下，竖向剪应力峰值随横观各向同性系数的增大而增大，并且随着深度从0.02 m增加到0.17 m，竖向剪应力先增大后减小；改建路面加铺层层底拉应力和土基竖向压应变随横观各向同性系数的增大而减小。旧沥青砼路面加铺沥青面层设计与施工中应适当考虑沥青横观各向同性的影响。