基于客户软时间窗的地下物流配送路径优化*

郭琪， 郑长江， 李锐

(河海大学 土木与交通学院， 江苏 南京 210098)

随着互联网的蓬勃发展，现有地面交通供应能力已无法满足物流配送的需求。为追求更高效、更高品质的服务，缓解交通压力，文献[1]利用地面与地下交通资源，提出软时间窗条件下地下物流配送优化模型。文献[2]指出在物流配送压力较大的城市，主要运输线路沿线大多开通了地铁，可在客流量不很大或非客运时段选取固定时间对快件进行通过运输，将货运中心、地铁中转站和客户点连成一个整体，结合时间窗对物流配送路径进行优化。由于硬时间窗的要求较严格，无法很好地处置货物堆积、列车早晚点等突发情况，地下物流系统在软时间窗下的路径优化成为主要研究课题。但研究集中在理论层面，实施难度较大。软时间窗主要是指地铁等严格遵守运行时刻表的运载工具在特定时间窗下进行物流运输，时间窗主要为列车运行时刻表。该文基于客户软时间窗建立地下物流成本最优模型，采用遗传算法进行迭代分析，对地下物流配送路径进行优化。

1 问题描述与建模

1.1 问题描述

以南京现有地铁线路为基础，考虑地下物流配送和地面车辆配送，使运输总成本最小，在尊重假设的前提下，运用改进遗传算法计算软时间窗下成本并与传统运输模式下成本进行对比，验证地下物流配送模式的可行性。

列车自配送中心起单方向运行负责物流配送，且不接受新的货物，到达相应的出站点时，卸载并由地面配送车辆运送至客户，地铁线路的货物集散中心、出站点和客户时间窗均已知，地面配送车辆容量及中转时间固定。

1.2 模型假设

(1) 货物配送中心可以有一个或多个，且同列货物同时发出。

(2) 地铁列车只负责配送货物，不考虑返回过程。

(3) 货物运输的同时不会影响乘客服务质量。

(4) 每趟列车及地面运输车的运输能力有限且已知，最大货运量不超过其容量。

(5) 每个地点的货物需求量已知，且只能有一条线路服务。

(6) 模型中时间窗只针对末端客户地铁列车的开行，地铁列车的开行配送均不考虑在其中。

(7) 地铁车辆运输成本和车辆运输成本与距离成正比，且车辆成本固定。

1.3 模型建立

1.3.1 运输时间成本

货物在地铁列车及末端配送车辆上运输途中均不产生时间成本，只有在客户时间窗外产生累积的情况下生成时间成本。具体情况如下：1) 在时间窗的最早时间之前送达，该批货物会因客户无法及时接受而堆积；2) 在时间窗最晚之后到站，客户会消耗等待时间。以上2种情况均计算在时间成本内，其他时间成本不计入模型中。时间成本模型如下：

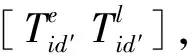
1.3.2 车辆成本

假设车辆成本包括地铁列车成本和地面物流车辆成本，均与开行趟数相关，与列车开行距离无关，则车辆成本为：

式中：Ccar为车辆成本；C1为每趟地铁列车的固定开行成本；C2为地面配送车辆每趟开行成本；Nv为地面配送车辆的总开行次数。

1.3.3 物流运输成本

物流运输成本包含地上和地下两部分，将运输过程中产生的相关费用平摊到运输单价中，且各相关配送点的快件需求量已知。运输成本模型如下:

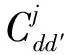
1.3.4 总成本模型

综合时间成本、车辆成本和货物运输成本，构建总成本模型如下：

minC=Ctime+Ccar+Ctrans

即：

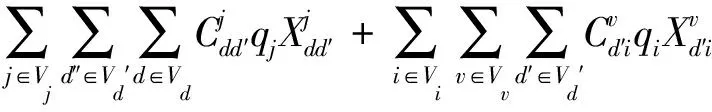
模型约束条件如下：

(1)

∀d′∈VD′，∀d∈VD

(2)

(3)

(4)

(5)

式(1)约束时间窗条件下时间早晚；式(2)表示2个变量均为0～1变量；式(3)表示每趟地铁列车所运输的货物不得超过其单次最大载运量；式(4)表示地面配送车辆每次配送的客户需求总量不超过其最大载运量；式(5)表示每个客户只服务一次，即地面配送车辆只经过一次。

该目标函数为线性函数，目标函数集为凸集，在可行域范围内存在最优可行解。

2 求解算法

2.1 求解步骤

采用遗传算法对模型进行求解，求解过程见图1。

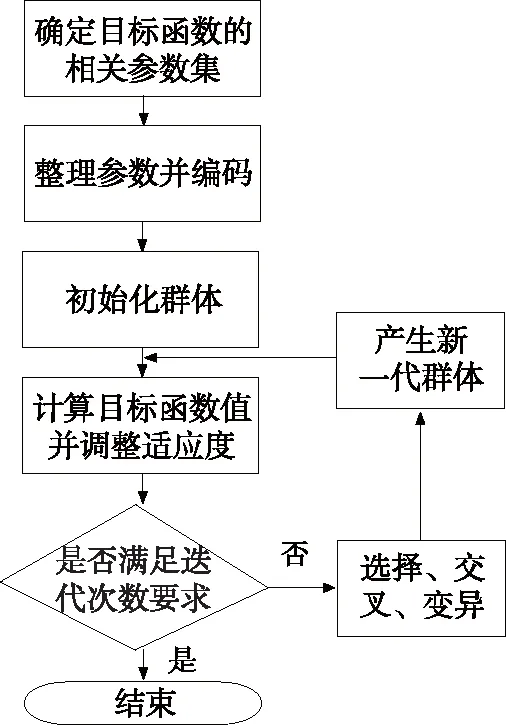
图1 模型的计算过程

2.2 算法主要术语

(1) 染色体。又称为基因型个体，一定数量的染色体组成群体。

(2) 适应度。个体对所处环境的适应程度，该算法中每个个体的适应度通过轮盘赌选择法获取，生成[0,1]之间的随机数作为适应度值。

(3) 选择。淘汰不好的个体，保留优质个体。

(4) 交叉。将父代个体的部分结构加以替换重组，产生新个体。

(5) 变异。群体中某些个体(串)的基因值发生变动。

3 实例计算与结果分析

南京南站是华东地区最大的高铁站，每天会有大量快件到达南站，再由地面配送车辆送到客户手中。借助南京南站现有地铁资源，可在不影响客运的前提下实现地下物流配送，减缓地面交通压力。地铁1号线经停的中转站有3个，分别为中华门站、珠江路站、迈皋桥站。3个车站服务的主要客户共29个，且每个客户每趟配送只有一次。统计客户需求时间作为软时间窗，即9：00—9：45和20：15—21:00，分别记为[0,45]、[45,90] min(见表1)。

表1 客户时间窗

运用上述模型，对相关参数进行定义，采用遗传算法对29个客户进行迭代求解，迭代次数为200次，种群规模为20个，交叉概率为0.8，变异概率为0.2。结合每个客户的需求量和时间窗，计算得到10条配送优化路径(见表2、图2)，优化过程见图3。由图3可知：实现带时间窗地下物流配送可有效节约配送时间，极大提高工作效率，缓解市区内因物流配送导致的交通压力。

表2 快件配送优化线路

图2 快件配送优化路径连线图

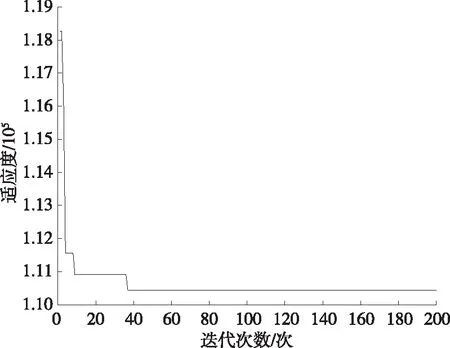
图3 路径优化过程

根据调查统计结果，近5年南京南站单独使用货车配送的平均配送时间为113.2 min/次，运输成本为21 039元/次。运用上述优化模型，采用地上、地下综合配送模式的平均消耗时间为32 min/次，运输成本为11 044元/次，分别比货车单独配送降低71.73%、47.51%，而且有效缓解了物流带来的运输压力。

4 结语

该文主要研究客户软时间窗条件下地下物流配送的路径优化。通过构建货物运输成本、车辆成本和时间成本综合最小的目标函数，引入遗传算法，采用MATLAB软件实现选择、交叉、变异等，得到优化的物流配送路径。与传统货车单独运输比较，客户软时间窗下地下物流配送可节约配送时间、降低配送成本。

文中未涉及地铁列车运行的时间窗，无法最贴切反映配送过程。地下综合物流配送系统模型还处于起步阶段，如何将多条配送线路相协调，实现取送货物双向运输，是未来研究方向。