基于概率和寿命周期成本的桥梁维护策略研究

曾 勇，王羽潇，谭红梅

(1.重庆交通大学 山区桥梁及隧道工程国家重点实验室，重庆 400074；2.重庆交通大学 山区桥梁结构与材料教育部工程研究中心，重庆 400074)

我国的桥梁管养任务逐渐加大，要求养护的桥梁日渐增加。处于服役中的桥梁受荷载效应、外部环境等因素的影响，其结构性能逐渐衰退，可靠度水平不断下降，严重影响了桥梁运营的安全。

寿命周期成本分析方法针对现有和新建桥梁结构的养护问题及难点，使设计人员和养护决策者考量现今做法的未来影响，以使养护资金取得最佳的经济效益[1-3]。在桥梁结构中运用寿命周期成本计算方法，对现有桥梁在一段规定时间内的养护，预期的总成本包括除了原始成本之外的所有成本。近段时期，有关桥梁寿命周期成本(Bridge Life Cycle Cost，BLCC)计算方法方面出现了较大进展，不少学者在桥梁设计规划、养护管理以及更新中广泛应用了寿命周期成本计算方法[4-7]。

受限于财力，桥梁管养投入的资金远不能够满足实际工程的需求。如何保持服役桥梁的良好工作性能，如何制定科学有效的桥梁管养规划与维修决策，如何科学有效地使用有限的养护资金，保证桥梁的安全稳定与交通顺畅，是当前桥梁管养重要的任务与难题。本文基于概率(可靠度)和桥梁寿命周期成本进行研究，分析讨论了桥梁的维护策略，以期减少桥梁养护费用，提高桥梁的性能。

1 基于概率的桥梁检测维修优化

鉴于结构寿命期性能，新结构系统的设计优化准则开始普遍采用最低预期生命周期成本[6-8]。桥梁的修补、修理、更新以及大修等统称为桥梁的维护，其在桥梁结构的整个使用生命期里均可能发生。桥梁的维护贯穿于桥梁结构的使用历程，并且还是保证结构正常服役不可或缺的方法和最基本的手段。在整个服役期内，桥梁结构安全状态是否可控与桥梁结构服役寿命能否预测是桥梁结构维护方法确立的基础。实际情况下，一般需要对维护的桥梁工程结构以及它的服役情况根据一定的时间间隔进行合理的检查与监测，全方位了解桥梁结构的服役状态、结构材料以及构件在服役环境中遭受的损害，掌握桥梁的安全性能。针对桥梁结构体系内产生损害或将要产生损害的结构构件实施必要的加固(增大结构的抗力，降低劣化速度)或减小结构可能承受的荷载等处理方法，见图1。

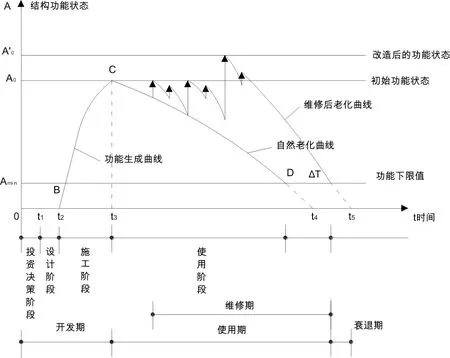
图1 桥梁构件全寿命期的维护策略示意图

经过恰当的维护优化，保证服役条件下桥梁结构的安全情况达到满意的程度。进行桥梁结构维护，需要对结构每一构件的功能失效以及失效模式均有一定的认识。结构在整体全部失效之前一般会经历几个状态，这是工程结构失效的主要特征，导致这几个状态出现的原因是结构内的一个或者几个结构构件服役性能降低。针对功能失效，较浅层面的保护性维护中所选取的结构检测就可以察觉将要出现失效的迹象，以便利用合理的维护方式来减缓桥梁失效情况的出现。

经典决策理论中的贝叶斯先后验决策分析能够解决确定最佳的检查和修理计划的策略问题[9]。据此，Faber[10]等人针对海洋结构物有关风险的检查规划进行了有益的研究。检测及维修决策问题的决策树模型如图2所示。一般来说设计工作寿命期TL内的检测次数n、检测时间间隔ΔT=(ΔT1,ΔT2,…,ΔTn)、检测质量q=(q1,q2,…,qn)、维修质量k=(k1,k2,…,kn)及检测的位置l=l(ΔT1),l(ΔT2)…l(ΔTn)可以用来定义检测和维修计划。为便于表示，将这5个参数用一个检测矢量i表示，则有i=(n,ΔT,q,k,l)。

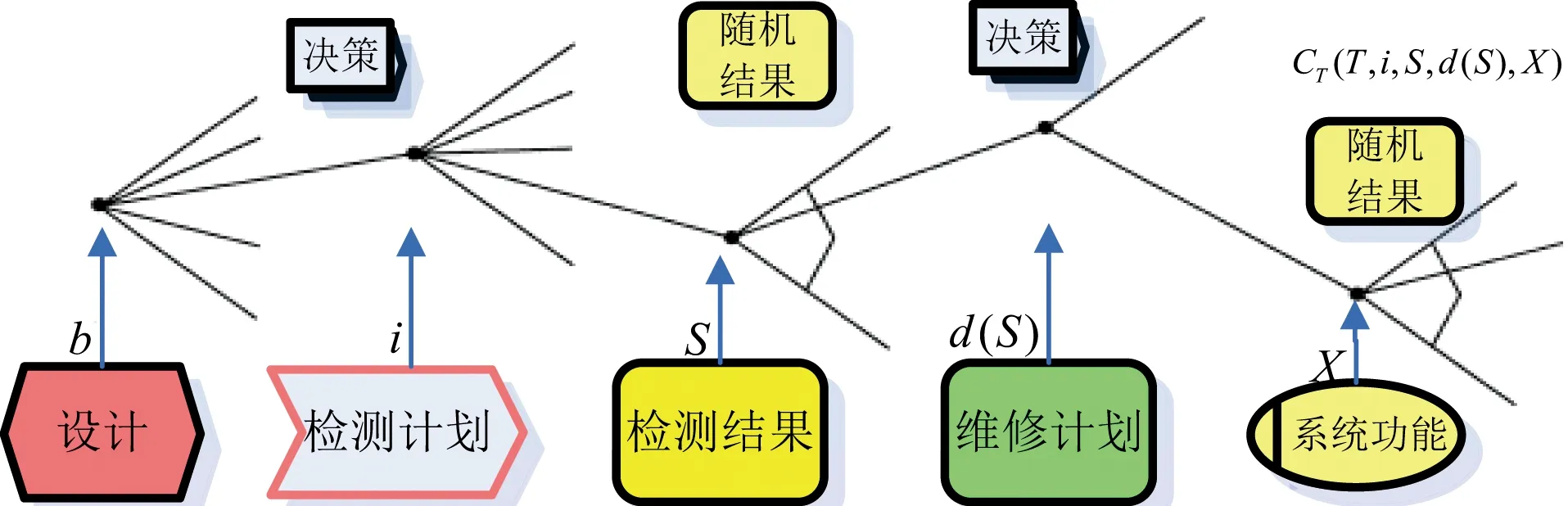
图2 检测及维修规划决策树

表示桥梁构件设计厚度的变量b，即为构件原始设计阶段的检测和维修规划里需要考虑的优化参数。未确定的检测结果(腐蚀厚度、裂纹尺寸)可以用随机矢量S=(S(ΔT1),S(ΔT2),…,S(ΔTn))来表示，因为检测功能自身的不确定性和结构损伤不确定性因素会产生影响。可以利用维修决策准则d(S)判定结构检测后有无维修的需求[10]。体现系统功能的不确定性的参数都可用矢量X=(X1,X2,…,Xn)表示。

全部预期费用包含原始设计和施工费用、检测费用、维修费用和失效费用[9]。桥梁的构件(如缆索的直径，钢箱梁的板厚，拉索用量等)在设计寿命期内达到最低可靠指标的情况下，使结构寿命周期内总的预期费用达到最低，这就是优化的目标函数。因此，可建立总的预期费用的优化模型:

(1)

式中:cT(b,i,d)是结构在设计寿命期内总的预期费用；CD(b)是结构原始的设计与施工费用；CI(b,i,d)是预期的结构检测费用；CR(b,i,d)是预期的结构维修费用；CU(b,i,d)是预期的结构用户费用；CF(b,i,d)是预期的结构失效费用；β(TL,b,i,d)是设计工作寿命期内的结构可靠指标；βmin是结构的最低可靠指标。

可以用结构的失效概率来计算可靠指标，见式(2)。

β(t)=-Φ-1(PF(t))

(2)

式(2)中，Φ-1(·)表示标准正态函数的反函数，PF(t)表示[0,t]内结构的失效概率。

对于处于服役阶段的桥梁，不同的检测及维修计划对桥梁结构的CD(b)影响较小。因此，式(1)的优化问题简化为如下的优化问题。

(3)

维修更换需要平衡结构安全和经济两个指标间的问题，也就是寻找最好的维修更换策略。即在确保结构安全、使用功能达标的条件下，结构获得的经济效益最佳[11-12]。基于最低费用的条件下取得最优的维护效果，就是桥梁维修单目标优化。普遍来说桥梁全寿命使用期内的养护费用最低就是优化的目标函数[13]，失效概率值、结构承载力水平、能接受的结构状态、结构剩余寿命等都是优化的约束条件。

在结构维修加固计划中，要注重计划的合理性，因此需要选取真实结构的时变可靠性作为控制参数。可靠度(概率)可以表示此次维修的目标与费用限制，也描述了关于结构维修的质量指标，协调好维修质量、近期投入和长期效益的关系，依赖于合理的结构可靠度选取。

维修是在桥梁整个寿命周期内，确保桥梁结构或构件充分的可靠和安全，并且在使用性能方面可以满足养护规范需求的一系列维修活动。是否进行下一步的维修，通常是在检测活动结束之后，依据检测结果来判断。

2 算例

将某吊杆钢丝的腐蚀维修作为目标，对钢丝的维修策略进行分析，步骤如下:

(1)构件的可靠度分析；(2)不同维修策略的影响；(3)必要性维修的时间间隔优化；(4)选择最优的维修策略。

假设钢丝发生均匀腐蚀，钢丝锈蚀的极限状态方程为:

Z(t)=dF-dc(t)

(4)

式(4)中：dF是钢丝容许的腐蚀深度；dc(t)是t时刻的钢丝腐蚀深度，即

d(t)=A(t-τ1)B

(5)

各基本参数的统计特性见表1。

表1 基本参数的统计特性

各费用(检测费用，更换费用以及失效费用)的比例关系假设见表2:

表2 各费用的比例取值

在进行分析时只需清楚各费用之间的比例关系，C0按照具体情况来取值。时变失效概率和可靠指标一般采用FORM方法，计算结果见图3、图4。

图3 钢丝的时变失效概率

图4 钢丝的时变可靠度曲线

分析3种维修策略的最优检测时间和年均费用CA。在3种维修策略中，必要性维修也称为被动维修，主动维修包含了基于使用维修和基于状况维修[14-15]。

(1)策略1:必要性维修

必要性维修也是被动维修、事后维修，它的优点是可以完全利用构件的寿命。必要性维修的特征是仅在日常养护时进行预防措施，一般情况下均是待构件损坏或失效后再进行修理。依据必要性维修的特征，这个策略主要适用于以下情况：①构件突然损坏或失效，不能预测，但损坏或失效的后果对于构件的安全性没有影响；②构件逐步损坏或失效，但损坏或失效的后果对于构件使用安全没有影响，其造成的损失比其他维修方式的费用低。

拉索钢丝一旦失效，就需要更换。采用必要性维修这一策略时，拉索钢丝在寿命期内的更换年限可选定为μ(tL)=20 a。

因此，年均预期费用为:

CA=(CR+CF)/μ(tL)

(6)

代入数据，则有CA=(1 000+1×105)C0/20=5 050C0。

(2)策略2:基于使用维修

基于使用维修的目的是为了降低构件损坏或失效的出现概率和减缓构件的功能衰退，其实施要根据事先确定的时间间隔或指定标准，亦称作周期性预防维修、定期维修。主动维修与周期性预防维修这两点是定期维修的特征。

假设拉索钢丝失效之前进行了维修行为，年均费用的计算公式为[11]:

(7)

TR是构件更换的间隔；PF(TR)是构件在TR时刻的失效概率；f(t)是构件失效的概率密度函数。假如失效概率的值较小，又当结构的寿命期大于检测间隔的时候，上式可化为:

CA=(CR+CFPF(TR))/TR

(8)

如果更换间隔较短，则年均更换费用相对较高，失效费用较低；如果更换间隔较长，则年均更换费用相对较低，失效费用较高；通过折中年均更换费用和失效费用可以得到最优的更换间隔。计算结果如图5所示，最优更换间隔为15 a，CA=82.27C0。

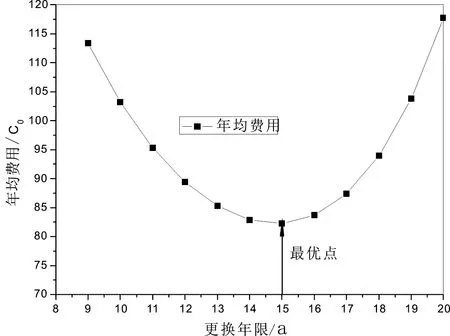
图5 最优检测间隔

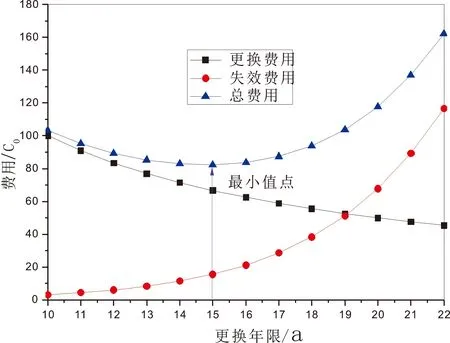
图6 各费用随更换年限的变化图

(3)策略3:基于状况维修

基于状况维修的主要特征是预测性维修、关键构件状态监测维修、主动性维修。以实时或接近实时评估构件的运营状况为基础，在构件产生了显著劣化后立即实行的维修策略称为基于状况维修。

基于状况维修以构件的失效产生有一个时间发展的过程为基础，是一种基于构件状态的维修方式。也就是说大多数失效情况在其将要出现时都有一些明显的征兆或信号，这些明显的征兆或信号就是潜在失效。如果能检测到这些明显的征兆或信号，就可以预测构件的失效，基于构件的状态可以采取措施，预防构件失效。状态维修综合了事后维修与以时间为基础的定期维修的特点。

如果拉索钢丝腐蚀深度高于允许值，但不高于失效值时，则应当用检测来判断钢丝更换的时刻。在失效费用不大的情况下，年均费用近似表示为:

CA=CI/Δtins+(CR+CFPF)/μ(tL)

(9)

式中：Δtins是检测间隔；μ(tL)是钢丝的预期寿命。

检测间隔一般定为2 a一次，所以在钢丝的20 a使用期中，至少应检测10次。因此，CA=106.78C0。

(4)最优维修策略

最低费用的维修方案是基于使用维修(策略2)的，因为其总费用最小，这一结论在确定基于使用维修(策略2)与基于状况维修(策略3)的最优检测时间间隔与更换时间间隔之后可得出。

必要性维修、基于使用维修和基于状态维修这几种策略在维修实际工作中经常采用。3个维修策略能同时采用，但针对不同的构件，其侧重点不同，所占的比例也不同。

选用何种维修策略主要依据维修对象的自身状况，还要考虑到维修技术、维修经费和维修手段等因素，以达到既经济又安全有效的目的。

3 结论

(1)在桥梁结构的养护中，结合概率和寿命周期成本，可以制定现有桥梁在一个时间段内的合理养护计划，预期的总成本包括除了原始成本之外的所有成本。经过恰当的维护优化，保证服役条件下桥梁结构的安全水平达到满意的程度，就是桥梁结构的维护目标。

(2)概率(可靠度)指标有两个含义，它是结构维修的质量指标，也是此次维修的费用限制，协调好近期投入和长期效益的关系，依赖于合理的维修可靠度选取。

(3)本文提出的维修优化策略也能够用于类似结构的养护管理。对于复杂结构而言，其结构退化复杂多变，因此决策优化问题是非常复杂的，值得进一步研究。