基于BFA-Elman的电力负荷可靠性预测系统设计

王明馨，郑瑛楠，邓卓夫

（1.沈阳农业大学 水利学院，辽宁 沈阳 110866；2.东北大学 软件学院，辽宁 沈阳 110169）

由于电能无法大量储存，通常情况下为即发即用[1]。因此准确的电力系统负荷预测可有效地平衡供需关系，并大幅度降低发电成本，有助于改善电力系统的经济效益，同时提高其环境效益[2]。在电力负荷预测方面，传统预测模型通常包括差分整合移动平均自回归模型、卡尔曼滤波模型、参数回归模型等[3]。随着人工智能技术的快速发展，神经网络、专家系统、支持向量机等模型在电力系统负荷预测中的应用已成为主流[4]。

Elman 神经网络在前馈神经网络中添加一层连接层作为单步延迟算子，以达到记忆的目的，并使该系统具有较为实用的时变特性，能够适用于电力负荷预测[5-6]。但对于未知的非线性模型容易陷入局部最优，仅具有非线性拟合能力的Elman 神经网络在寻优方面仍有待加强[7]。近年来，神经网络的非线性拟合能力与智能算法的非线性优化相结合已成为解决非线性模型的趋势[8]，但部分研究对于负荷预测的效率及准确度仍有待提升[9]。

因此，文中采用细菌觅食算法（Bacterial Foraging Algorithm，BFA）改进Elman 神经网络，构建了基于BFA-Elman的电力负荷可靠性预测系统，并通过实验分析验证系统预测的准确性和高效性。

1 电力负荷可靠性预测系统

1.1 Elman神经网络

通常而言，Elman 神经网络依次包含输入层、隐藏层、接收层以及输出层4 层网络。其具体结构如图1 所示。

图1 Elman神经网络结构图

输入层起到信号传输的作用，而输出层起到线性权重的作用[10-11]。隐藏层的传递函数可以采用线性函数或非线性函数，承接层用于存储前一时刻隐藏层的输出值，并返回到网络的输入[12]。

Elman 神经网络的非线性状态空间表达式为：

式中，x、y、u分别表示中间层、输出层以及输入层的节点向量；xc(k)是承接层的反馈向量；ω1、ω2、ω3分别是承接层连接中间层、输入层连接中间层、中间层连接输出层的权重。

1.2 BFA

2002 年Kevin M.Passino 基于大肠杆菌在人体肠道内吞噬食物的觅食行为，提出了一种仿生优化算法—细菌觅食算法（BFA），该算法的核心机制包括趋向、繁殖和迁移等操作[13]。

1）趋向：个体适应度可以通过游动和翻转进行改善。游动过程不改变个体方向，当适应度不能再通过游动改善时则进行翻转，使游动方向随机改变。具体表达如下：

式中，j、k、l分别为趋化次数、繁殖次数和迁移次数；θi(j,k,l)为个体i在对应次数的趋化、繁殖和迁移后的位置；S(i)与ϕ(j)分别为个体i游动步长及随机翻转后的方向。

2）繁殖：根据适应度对个体进行排序，并选择适应度靠前的个体为繁殖操作的父代。在不考虑变异的情况下，子代个体将继承父代个体的所有属性。

3）迁移：适应度较差的个体新位置按迁移概率进行随机选取。

1.3 基于BFA-Elman的电力负荷可靠性预测

定义t时刻网络的权值调整误差函数为：

式中，y(t)与yd(t)分别为第i个输出节点的期望输出和实际输出。

将E(t)对ω3求偏导，可得：

同样，将误差函数E(t)对权值ω2、ω1进行求偏导。由可以得到BFA-Elman 神经网络学习算法，计算过程为：

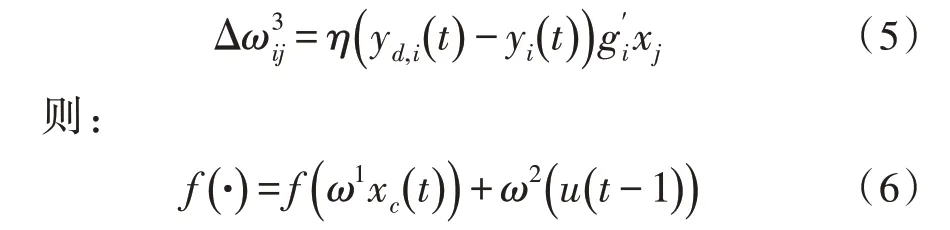
Elman 神经网络算法的性能受诸多因素影响，主要包括学习算法、激励函数、初始时各层的权值和阈值以及网络结构等。因此，为了获得更优的预测精度，利用BFA 算法对Elman 神经网络进行改进。BFA 在处理高维度问题时能够避免早熟收敛，其具有较高的寻优效率[14]。因此，利用BFA 算法对Elman的权值和阈值进行改进，解决其本身拓扑结构的多样性和权值阈值的不确定性问题[15-16]。基于BFAElman的电力负荷可靠性预测流程如图2 所示。

图2 基于BFA-Elman的电力负荷可靠性预测流程

在进行可靠预测时，首先对电力负荷的历史数据进行预处理，然后利用BFA 改进Elman 神经网络，得到最优的权值阈值。最终将预处理后的电力数据输入优化后的Elman网络，以实现电力负荷的可靠预测。

2 数据预处理

2.1 异常数据剔除

由于各个环节均可能存在数据丢失、缺损的情况，从而造成异常数据的产生，而这都有可能影响预测模型的精度。电力负荷具有一定的周期性，在同一时刻负荷具有一定的相似性，其变化范围波动较小。若超出这一范围，则可判定为异常数据，表达如下：

式中，x(i,t)为第t个时刻的负荷值；ϑ(t)为阈值，其根据实际情况可预先设定。

当检测出异常数据后，通过对突变负荷的平滑处理，可使得数据波动较小。具体处理如下：

式中，(t)为负荷平均值。

2.2 数据标准化

输入输出数据的直接差异较大容易导致严重的预测误差，因此对所有数据进行了归一化处理如下：

式中，xmax、xmin分别是数据的最大值和最小值；xi、分别是归一化前后的数据。根据式（10）对优化后的Elman 神经网络的预测数据进行反向归一化，以获得预测负荷值：

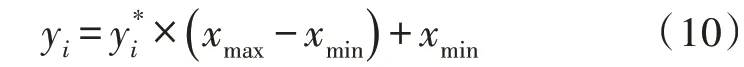
式中，yi和分别是逆归一化前、后的预测数据。

3 实验结果与分析

实验中使用了某省市一天内的实际电力负载数据，每半小时收集一次，共48 组数据。同时选择30天总共1 440 个数据作为实验数据，如图3 所示。

图3 电力负荷历史数据信息

实验中，使用单步滚动预测模型，选择第一批1 383 个样本作为训练集，最终选择了48 个样本作为测试集。Elman神经网络设置为9-11-1结构，输入层中的神经元数量为9；隐藏层中的神经元数量为11；输出层中的神经元数量为1。误差设置为0.000 1，最大训练频率为2 000 次/s。

3.1 计算量分析

为了论证BFA-Elman 神经网络的寻优性能，将其与传统Elman 神经网络在预测所需时间上进行对比。数据量对预测时间的影响如图4 所示。

图4 数据量对预测时间的影响分析

由图4 可知，当数据样本较小时则两种算法所需预测时间相差较小。甚至传统Elman 网络所需要的时间略优于BFA-Elman 网络模型。因此所提模型在小样本集下仍需利用BFA 进行寻优，影响了其预测速度。但随着样本集的增大，预测算法所需的迭代时间有了明显不同。传统Elman 网络受数据量的影响较大，而所提BFA-Elman 网络的处理则能力较强。当数据量为10 240 MB 时，完成负荷预测的时间不超过20 s。

3.2 预测准确率

对优化前后的Elman 神经网络模型分别进行负荷预测。其预测结果准确率如图5 所示。

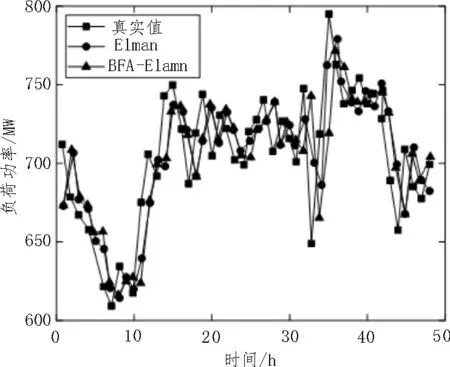
图5 优化前后的负荷预测曲线对比

从图5 中可看出，所提BFA-Elman 网络得到的负荷预测值与真实值尤为接近，而Elman 网络与真实值存在一定的偏差。因此，所提模型采用BFA 算法优化Elman的网络参数，能够提高预测的精度。

为了定量分析所提模型的预测性能，将其与Elman 网络预测值的相对误差进行对比分析。以选取一天的负荷数据为例，结果见表1 所示。

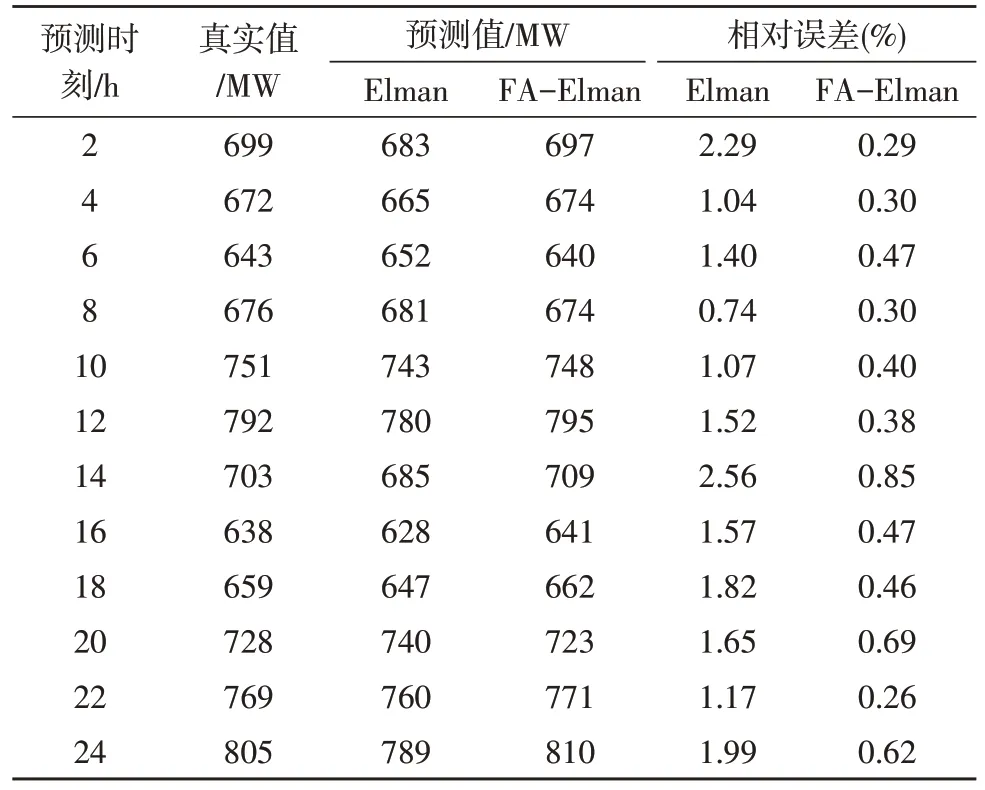
表1 负荷预测相对误差对比

由表1 可知，通过BFA 优化权值和阈值，能够显著提高模型的预测性能。基于Elman 神经网络的平均预测绝对误差为1.45%，最大预测绝对误差为2.56%。BFA-Elman 神经网络的平均预测绝对误差为0.41%，最大预测绝对误差0.69%。可以看出，采用BFA-Elman 神经网络可以有效提高预测精度。

4 结束语

负荷预测可靠性的提高对于提升发电设备的利用率和经济调度均具有重要意义。为此，文中设计了一种基于BFA-Elman 电力负荷可靠性的预测系统。通过BFA 优化Elman 网络模型的结构参数获得最佳的权值和阈值，并利用BFA-Elman 网络构建电力负荷预测模型，以实现可靠预测。实验结果表明，预测误差均值为0.41%，低于对比方法。由于文中只考虑了短期电力负荷，对于更长时间的预测缺乏研究。在接下来的工作中，将通过优化预测模型提高更长时间电力负荷预测的可靠性。