基于改进蜂群算法的医疗人力资源应急优化配置方法研究
2022-04-13姜鑫磊
姜鑫磊
(河北北方学院附属第二医院,河北张家口 075100)
在全球化的疫情背景下,无疫情地区的正常医疗服务保障对于维持我国社会稳定、保障突发性疫情扩散具有重要意义。我国医疗行业的竞争力从单一的医疗团队素质、诊断水平与外部环境拓展为全方位的综合能力,人力资源管理水平就是决定突发紧急情况下医疗行业平稳运营的重要因素。加强医疗人力资源的配置,对应对突发医疗负担的考验,具有重要意义。
为解决紧急突发情况下的医疗人力资源配置问题,文中引入了约束编程,一方面明确了问题所涉及的约束描述方法;另一方面,通过实验分析,提出了解决问题的启发式算法。
文中首先建立基于多目标约束的人力资源配置模型[1-2],在分析了模型的局部与全局约束后,通过引入改进蜂群算法对该问题完成求解,并根据实验情况调整部分算法的结构参数。
1 人力资源问题建模
为将先前描述的问题建模为约束满足问题,将所有问题组件转换为<变量,域,约束>形式。建模可以通过多种方式完成,文中提出一种基于变量的模型[3],定义问题变量为个体i的时隙p,例如=sj表示将个体i分配给周期为p的服务是sj。定义该变量的主要原因是人力资源配置的解决方案必须是对所有个体在整个时期内的完整分配[4-5]。
1.1 完整性约束
对于人力资源集合中的任意个体,需满足[6]:

设域D={s1,s2,…,sn},人力资源分配单元(UH)中,n个分配单元集合是所有约束满足问题变量的域。=sj表示个体i在服务周期sj内受时间阶段p的影响[7]。
1.2 约束条件
如上节所述,该问题有两种类型的约束:第一种类型表示与个体相关的约束,用于确定个体与自身周期的关系;第二种描述个体与其所处服务之间的关系。
为合理表达上述约束,文中考虑人力资源合集的强制性服务列表中为所有个体提供的固定义务服务数量m(m∈[1,|OS|]),对于任意的人力资源个体,应满足下述公式[8]:

此外,该模型仍需满足基本约束:每个个体在给定的时间段p中均拥有基本服务si,以及在下一个时期分配个体p+1 到服务si。对于任意一个基础的服务FS=

对于任意个体在资源分配的最后阶段,限制条件应满足下述公式:

在全局约束中,由于规划容量限制,所以每个服务容量均不能超过约束条件。即对于任意s∈services以及任意p∈[1,∣Periods∣],应满足下述约束:

1.3 优化目标建模
服务占用率对于解决方案的质量具有重要的意义。因此对于每项服务i,定义Oi为占用率,Ci为其容量,Ei为超出值:

上式需满足Ei≤0,即要维持i的容量;否则,服务将过载。后续的操作旨在确保尽可能维持或最小程度地破坏服务容量。因此对于任意服务i,任意周期内p,全局约束将由目标函数Minimize()代替。
2 基于改进蜂群算法的优化方法
为解决提出的人力资源优化问题,引入了蜂群算法。在标准蜂群算法中,所用蜜蜂的数量等于旁观者蜜蜂数量,即其数量等于蜜蜂总数的一半[9]。为了模拟自然界中的蜜蜂运动方式,改进蜂群算法中定义了不同的参数,包括蜜蜂编号(BN)、食物来源编号(SN)、重复次数(MCN)、为产生新答案而变化的变量数量(Ndim)以及失败数量上限[10]。
在人工蜂群算法中,若新的目标函数值改变,则需要重新设计解决方案,并用新的解决方案替换旧的解决方案[11]。但若新的目标函数值未显示任何改善,则主要解决方案仍存在。为改善这样的问题,提出了基于标准蜂群算法的改进方法。通过将旁观者蜜蜂的数量设置为蜜蜂总数的不同百分比,并选取最佳百分比[12],因此蜂群方程辅助解变为:
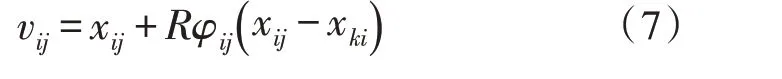
其中,R为邻域半径,其他参数已预先定义。提出了以下方程式以确定邻域半径[13]:

其中,cycle为迭代次数,MCN为迭代总数,A和G为预先设定的常数。
与标准蜂群算法相比,改进蜂群算法(IABC)的特殊优势如下[14]:其可以更优地进行蜂群侦察蜜源与获取蜜源之间的交互。应该注意的是,蜂群侦察是算法广泛探索问题的空间搜索能力,获取蜜源是算法探索局部解决方案邻域附近的能力。为了在蜂群侦察蜜源与获取蜜源间寻找平衡,通过对两种改进蜂群算法进行对比,选取符合实际应用标准的改进算法[15]。
在此,提出了两种后缀为1和2的部分约束改良人工蜂群(PCIABC)算法,将其分别称为PCIABC1、PCIABC2。通过分析论证,设计实验考察两种改进方法[16]。
在PCIABC1 改进算法中,人力资源库的每个尺寸参数表示在每个操作时间段分配的人力资源。在运行时间段,人力资源总数保持不变,使用连续性方程和人力资源总数约束条件来计算人力资源的高维新边界,代表每个运行时间段的人力资源储备,因此可以获得以下方程式:

根据上式可推导出用于选取在每个运行时间段t内人力资源的分配方法:
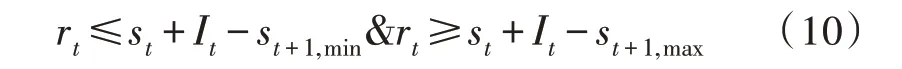
将此新界限与原始人力资源分配约束相结合,产生新的人力资源分配约束如下所示:

由实验可知,使用上式得到的解是可行的。在改进算法的第二种形式PCIABC2 中,解决方案的每个维度代表每个操作时间段结束时剩余的人力资源。假设在操作时间段开始时已知人力资源数目,则使用连续性方程计算人力资源的高维边界,以表示每个操作时间段结束时人力资源的剩余情况和限制分配约束。使用连续性方程来计算在时间段t内的人力资源分配量,并将该值替换为分配约束条件,可获得以下不等式:

对于每个分配时间段t结束时人力资源的剩余量,综合考虑新界限与原始人力资源约束条件,将产生新的人力资源释放约束条件,如下所示:

经数值实验测试可知,上式得出的解是可行的。
3 实验验证
下面结合实验针对实际情况以调整算法的实际运行逻辑,从而得出最佳解决方案。
在突发紧急情况下,数据可视化在人力资源分配过程中扮演着重要的角色,对于掌控实时人力资源配置结果,辅助调度决策具有重要意义。目前常用的通用可视化工具是GIS,它可以在各类地图中以多种可视方式显示数据。但仅依靠GIS 可视化软件难以获得更多的免费数据计算和分析,因此在编写人力资源可视化与调配软件时,使用C#编程中嵌入的ArcGIS Engine 构建一个特殊的GIS 应用程序,以实现数据的空间可视化。该界面实现了多种自由控制模式,支持调整显示时间范围、区域范围和人力类型范围并执行区域统计。
可视化软件后端基于Fc-means 聚类算法和简单线性迭代聚类(SLIC)算法优化了数据的计算与聚类,以便该聚类算法可以平衡数据的空间位置和人力资源流动。优化聚类的网络结构如图1 所示。

图1 优化结构图
为了改进先前专注于服务端的优化模型,通过提出一种针对人力资源的改进模型来处理涉及人力端的另一个优化模型。提出了基于Pareto front citepareto 方法的多目标优化模型,该模型可以通过改进之前的模型处理人力资源分配策略。
为改进多目标优化算法,添加了另一个客观约束,代表人力资源分配的偏好。因此,目标函数改为:
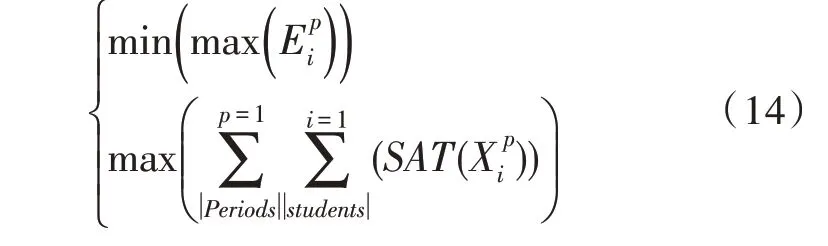
在统计实验中,人力资源管理者在6 个调度周期中选择两个不同的周期,并使用优化场景对先前的配置进行实验。图2 与图3 分别为单目标优化模型和多目标优化模型实验的结果。

图2 单目标优化实验结果
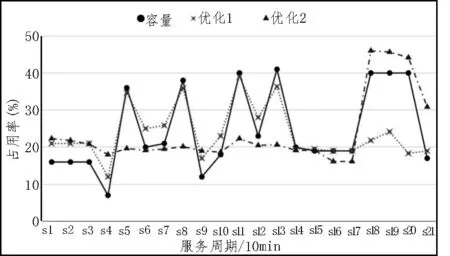
图3 多目标优化实验结果
通过分析可知,所选择的偏好模型满足了59%的人力资源管理者(10%的人力资源管理者完全满意,49%的人力资源管理者部分满意)。由于所设计方法中对目标设置进行了优化处理,所以多目标满意度实验结果也体现出了该算法可以同时优化服务和管理者的满意度。
表1 为对设计的多目标模型进行2 000 万次调度执行,通过硬约束或设置上限阈值等方法,将最大超过容量限制在27%以下的迭代计算实验结果。
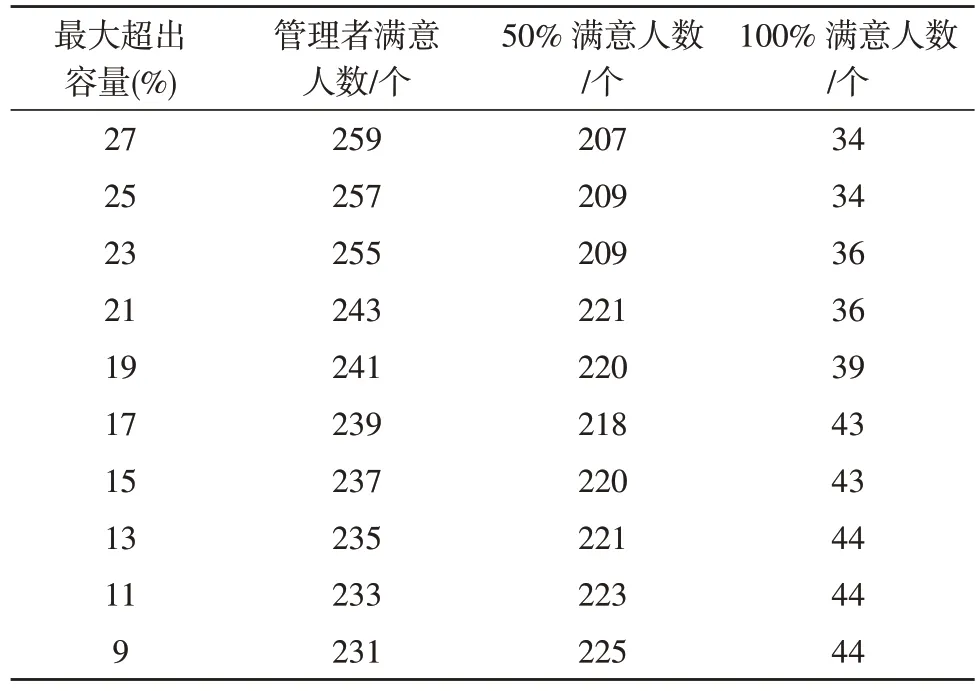
表1 管理者满意度与容量溢出对比实验
图4 为将极限时间固定为20 min 时,所有可能解决方案中最大服务溢出能力与管理者满意人数的关系,体现出了该模型的Pareto 边界。从图中可以看出两个目标函数是相关的,因此需要对多目标同步优化,这对所提方法的具体应用具有重要的指导意义。

图4 最大服务溢出能力
4 结束语
文中研究了在突发紧急公共卫生危机的情况下,医疗系统分配人力资源的实际方法。通过将此问题建模为多目标优化问题,并使用蜂群算法进行建模,完成智能化的人力资源优化配置。实验结果证明,通过将突发紧急情况的服务需求转换为多目标优化问题的软约束,能够达到良好的服务溢出效果,以实现无疫情区域的医疗人力资源的合理调度。
