一种多帧头联合自相关DTMB⁃A 频谱感知算法

黄云川，张 超，2，潘长勇，2

（1.清华大学 电子工程系，北京 100084；2.北京信息科学与技术国家研究中心，北京 100084）

0 引言

频谱感知技术可以获取频谱空穴的实时信息，从而使认知无线电系统高效地利用频谱资源。数字电视频带是认知无线电技术中的常用频带之一，在低信噪比环境中对相关频带内的主用户信号进行频谱感知是认知无线电技术中的一项重要课题。DTMB⁃A 是由清华大学数字电视技术研究团队和北京数字电视国家工程实验室联合开发的DTMB 系统的演进版本。2019年12 月，DTMB⁃A 被采用为国际电信盟（ITU）最新公布的全球第二代数字电视传输标准之一，与欧洲DVB⁃T2、美国ATSC 3.0 并列为国际三大第二代数字电视标准，目前已在多个国家和地区得到广泛应用。

目前，对于数字电视频带内的频谱感知问题，许多研究人员针对不同的标准和场景提出了一系列有效的解决方案。文献[2⁃3]分别针对DVB⁃T 和ATSC 标准给出了相应场景下的频谱感知算法，但由于这两种标准的帧结构与我国自主研发的DTMB 系列标准并不兼容，因此上述文献所提出的算法并不具备普适性。文献[4]针对DTMB 系统，取帧头伪随机序列自相关（PNAC）为判决统计量用于频谱感知，该算法仅仅利用了感知时间内间隔固定的自相关结果，因此其感知性能不够理想。而文献[5]采用本地的PN 序列与帧头序列进行互相关，即伪随机序列互相关（PNCC）算法。这种算法在相同条件下可以得到比PNAC 算法更多的判决统计量；然而其缺点是对环境引入的载波频偏较为敏感，检测中较小的频偏干扰会使得统计量大幅下降，抗干扰性较差。考虑到DTMB⁃A 系统工作时可能接触的环境干扰因素，需要在实际应用场合采取一种兼顾有效性和抗干扰性的频谱感知算法。

1 DTMB⁃A 系统帧结构

DTMB⁃A 系统物理层信道可以划分为若干个复帧，每个复帧包括同步信道、控制信道和数据信道。控制帧和数据帧的结构相同，每帧又包含帧头和帧体，采用OFDM 调制方案。其中，帧头部分为2 个长度为的伪随机PN⁃MC 序列，用于保护帧体以及信道同步。PN⁃MC 序列是由多载波频域二值序列（即长度为256，512，1024 的PN 序列）经过频域位置置换以及IDFT 变换生成的序列。帧体长度可以根据不同的应用环境分别取4096，8192 和32768，可 以 取的14～1256。DTMB⁃A 的帧结构如图1 所示。

图1 DTMB⁃A 系统帧、帧头序列结构

2 信号模型

设[]为经过无线信道后的DTMB⁃A 信号，考虑载波频偏和高斯噪声，接收采样序列[]的表达式为：

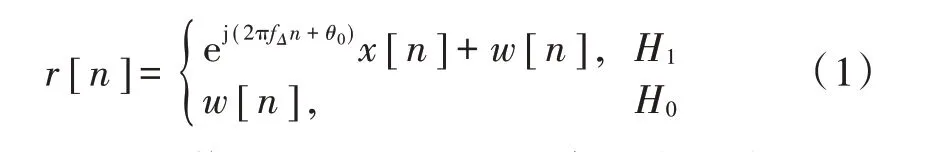
式中：[]表示均值为0、方差为的高斯白噪声；f表示归一化载波频偏；表示初始相位。在假设下，[]包含加噪的DTMB⁃A 信号；而在假设下，[]仅仅包含高斯白噪声。

3 多帧联合自相关算法

如前所述，现有的频谱感知算法中，PNAC 算法未能充分利用感知时间获取信号的有效信息，检测性能不够理想；而PNCC 算法又因为引入互相关运算导致其硬件复杂度过高。实际上，延长感知时间是提升频谱感知性能最直接的一种方法，但是由于在某些场合对感知的实时性有很高要求，这种方法通常不作为工程中的首选考虑。本节介绍一种对DTMB⁃A 信号的频谱感知算法，即多帧联合自相关（DIPNAC）算法。该算法在现有的PNAC 算法基础上，将不同帧间隔的自相关结果累积起来作为检测统计量，从而显著提升了检测灵敏度。

3.1 算法概述

1）考虑到DTMB⁃A 超帧中每个信号帧头是相同的，因此首先对接收序列作相关间隔为帧、相关长度和帧头长度一致的自相关，从处起始的自相关结果记为(,)，则有：

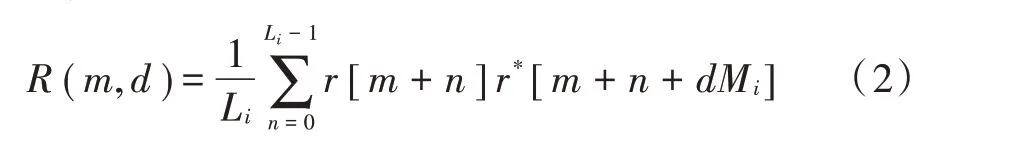
2）计算累积自相关(,)。如图2 所示，对感知时间内得到的(,)求和。记相关间隔为帧的自相关(,)个数为S，则(,)可以写为：

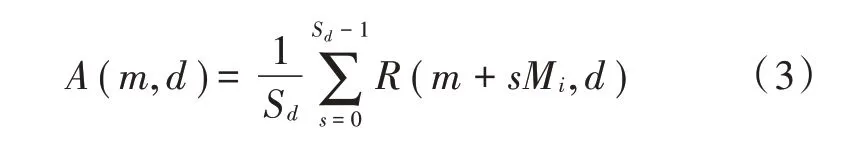
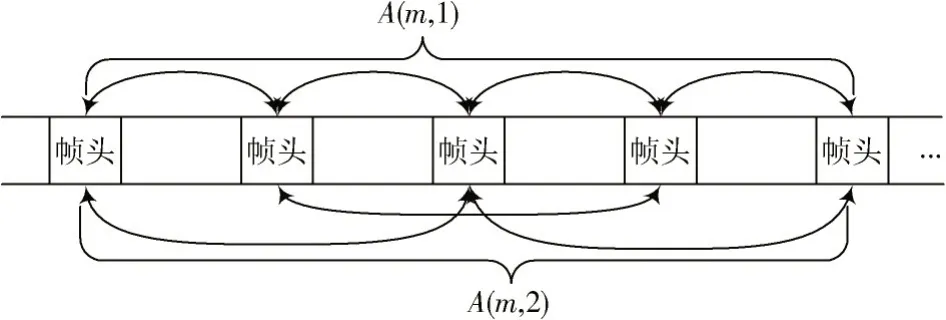
图2 不等间隔累积自相关示意图

3）去除相位旋转影响。由于(,)中包含与相关间隔有关的因子()=e ，直接相加可能导致自相关峰值产生损耗，因此需要消除相关间隔的影响，定义中间量(,)为：

取不同相关间隔分别计算(,)并记(,)的个数为，之后作加权求和得到联合统计量()：

式中权系数λ的选取要使得()在，两种假设下的分布差异性最大。这是一个带约束的优化问题，文献[6]指出其取值应为：

4）计算判决统计量。考虑到起始位置是随机选取在处，这并不一定是帧头开始的位置，因此将遍历一帧的长度，得到最终的判决统计量：

3.2 算法的判决门限

在假设下，()服从均值为0 的复高斯分布，因此其模值 ||() 服从Rayleigh 分布，而第3.1 节得到的服从Rayleigh 分布叠加后的联合分布。假设采用不同初始位置得到的()相互之间是统计独立的，可以近似得到的累积分布函数表达式：

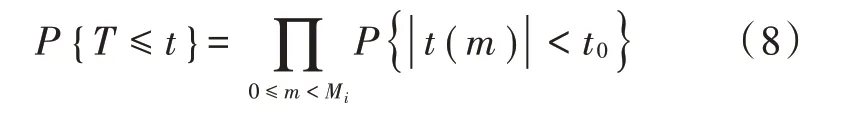
考虑到 ||() 服从Rayleigh 分布，有：

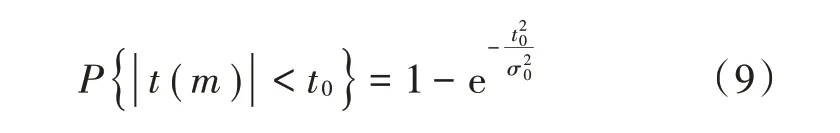
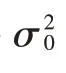
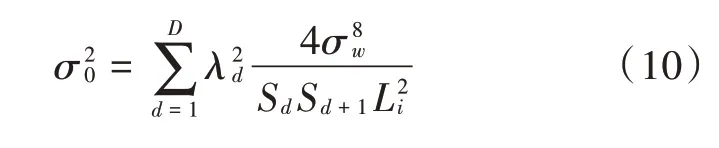
对于特定的虚警概率，其判决门限γ为：

3.3 漏检概率分析

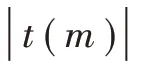
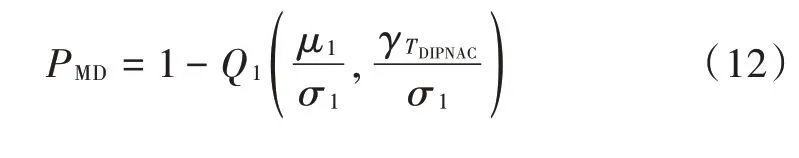
式中：

(,)表示Marcum Q 函数，表达式为：

式中()为零阶Bessel 函数。

3.4 DTMB⁃A 系统频谱感知的步骤

根据以上推导分析，基于DIPNAC 算法的DTMB⁃A频谱感知步骤可以用图3 所示的流程来表示。

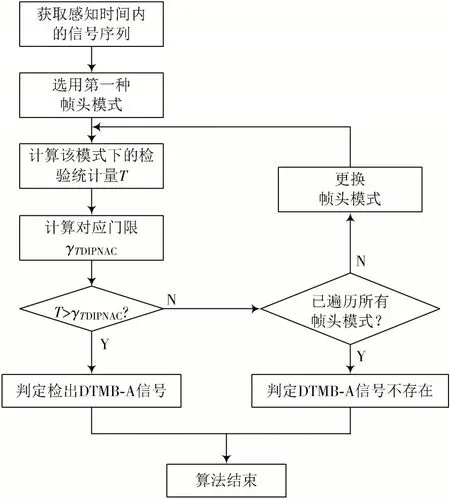
图3 DTMB⁃A 的频谱感知流程

4 仿真结果与分析

下面通过仿真结果来说明在DTMB⁃A 频谱感知中DIPNAC 算法的感知性能。和文献[7]的参数设置保持一致，本文采用恒虚警检测，检测参数如表1 所示。在Matlab R2019b 平台上，分别对PNAC、PNCC 和DIPNAC算法在不同信噪比和载波频偏参数下进行仿真比较。

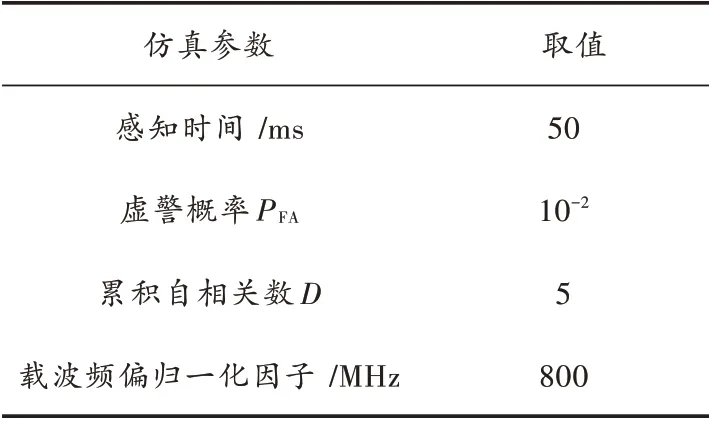
表1 仿真参数设置

针对帧头长512 模式（即=256），首先在AWGN信道条件下测试三种算法的检测性能，设置载波频偏分别为20 ppm 和30 ppm，其结果如图4 所示。图4 中横坐标为信噪比，纵坐标为漏检概率。由图4 可见：当载波频偏为20 ppm 时，由于相同信噪比对应的漏检概率更小，DIPNAC 算法的性能要优于PNAC 和PNCC 算法；但当载波频偏参数上升到30 ppm 时，PNCC 算法的检测效果大幅恶化，曲线在=10水平性能恶化约4.2 dB，而PNAC 算法和所提DIPNAC 的性能受载波频偏参数的影响很小，性能曲线无明显变化。这说明本文算法在满足检测性能的同时也具备载波频偏环境下的抗干扰特性。

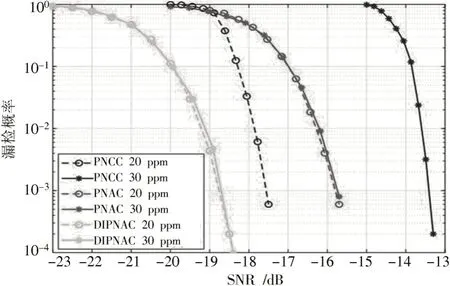
图4 不同载波频偏下三种算法的仿真性能曲线（信道：AWGN）

当信号经多径信道传输后，相应的频谱算法会面临一定的性能衰减。广电8 信道（SARFT 8）是一类单频网多径信道模型，其包络延时参数如表2 所示。

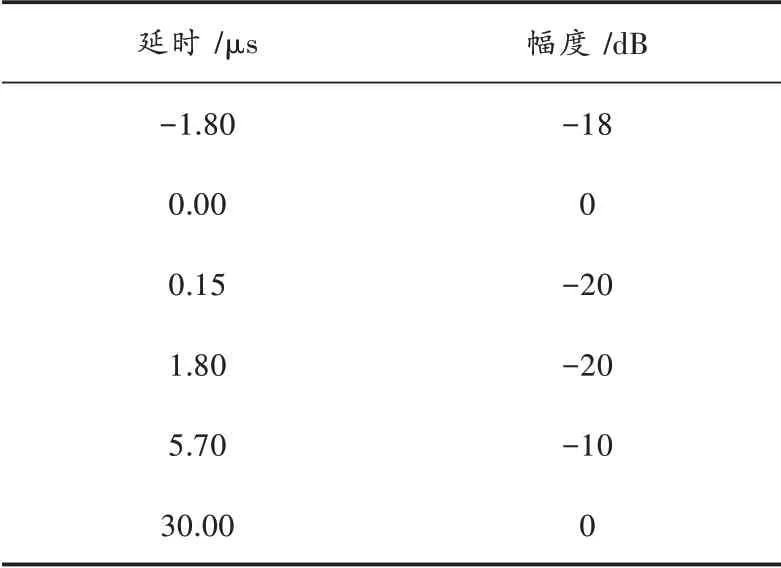
表2 SARFT 8 多径信道的包络时延参数

在SARFT 8 信道条件下，包括DIPNAC 在内的三种算法检测性能曲线如图5 所示。

图5 SARFT 8 多径信道下三种算法的仿真性能曲线

图5 的横坐标为信噪比，纵坐标为漏检概率。各算法的载波频偏均设置为20 ppm，其余仿真参数与前文保持一致。

从图5 可见：首先，DIPNAC 算法的检测性能在其他参数相同的条件下要优于另外两种算法；其次，由于多径信道的衰落效应，PNCC 算法在SARFT 8 信道条件下的性能出现显著恶化，但PNAC 算法和DIPNAC 算法受多径效应的影响效果不明显。为了使得漏检概率下降到10水平，在AWGN 和SARFT 8 信道条件下各算法所需的最小信噪比如表3 所示。由表3 可知，DIPNAC算法在AWGN 信道条件下分别比PNAC 和PNCC 的性能提升2.8 dB，0.9 dB。上述结果表明，在多径信道条件下，DIPNAC 算法同样具有相对较好的检测性能和抗多径干扰性能。

表3 三种算法漏检概率降至10-3水平所需最小信噪比 dB

三种算法的复杂度分析结果如表4 所示，这里复杂度的评价指标为硬件中实现单次检测的复乘次数（DTMB⁃A 的基本信号帧数目为）。由于自相关运算的过程可以利用前一次的自相关结果，其复杂度远远小于互相关运算，因此PNCC 的复杂度要远远高于其他两种算法。PNAC 算法具有最低的复杂度，但一系列仿真结果表明其检测性能仍有不足。而本文中DIPNAC 算法复杂度为PNAC 算法的倍，作为可调的因子来实现算法检测性能和复杂度的折中平衡。另外，当=1 时DIPNAC 算法和PNAC 算法完全相同，可以认为DIPNAC算法是对PNAC 算法的扩展延伸，即用可接受的计算复杂度为代价换取更优的检测性能。

表4 三种算法的复杂度分析

5 结 语

频谱感知技术在认知无线电的研究领域中发挥着重要作用。本文在前人研究工作的基础上，针对我国自主研发的DTMB⁃A 系统，提出一种基于帧头PN⁃MC 序列的多帧联合自相关算法。该算法能够充分利用感知时间内的有效信息，以较小的计算复杂度换取优越的检测性能，在多径信道环境和载波频偏情况下具备良好的抗干扰特性，为数字电视系统在相关频带内正常接入工作提供了可靠的理论基础。

由于本文采取的主要还是单节点检测方案，考虑到实际应用场景中的隐藏终端等问题，需要采用多节点协作感知来提升可靠性，未来将针对这一情形展开更为深入的研究。