Theoretical calculation of the quadratic Zeeman shift coefficient of the 3Po0 clock state for strontium optical lattice clock

Benquan Lu(卢本全) Xiaotong Lu(卢晓同) Jiguang Li(李冀光) and Hong Chang(常宏)

1National Time Service Center,Xi’an 710000,China

2The University of Chinese Academy of Sciences,Beijing 100088,China

3Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

Keywords: optical lattice clock,quadratic Zeeman shift coefficient,strontium

1. Introduction

The precision of the87Sr optical lattice clock has achieved the 10-18level.[1,2]In strontium optical clock, the 5s21S0-5s5p3Po0clock transition which has a natural linewidth of about 1 mHz is induced by the external magnetic field or the internal magnetic field-the hyperfine interaction.[3]The magnetic or hyperfine interactions break the spatial symmetry of the electric states, and lead to a mixing of the3Po0clock state and other states with the same parity but different angular momenta. To obtain a high precision of the optical clock,we should carefully estimate the external field effects on the clock transition as it is susceptible to the ambient environment around atoms. The external magnetic field is one of the essential factors in evaluating the uncertainty of the clock transition frequency.

For the strontium optical lattice clock, the Zeeman shift is rooted in the interaction between the atom and the external magnetic field. This brings an inconsistent Zeeman shift between the ground and excited states in the same magnetic field, which finally causes a shift of the clock transition frequency. In the88Sr optical lattice clock, we should estimate not only the first-order Zeeman shift,but also the second-order(quadratic)Zeeman shift. The first-order Zeeman shift,which is proportional to the magnetic field intensity,can be estimated by accurately determining the Land´eg-factor of the clock states and the external magnetic field strength. The quadratic Zeeman shift is proportional to the quadratic Zeeman shift coefficient (QZSC)C2and the square of the magnetic field strength. In the87Sr optical lattice clock, the first-order Zeeman shift could almost be canceled by stabilizing the clock laser to the average frequency of1S0,F=9/2,MF=+9/2-3Po0,F=9/2,MF=+9/2 and1S0,F=9/2,MF=-9/2-3Po0,F=9/2,MF=-9/2 transitions. The Land´eg-factors have been widely determined in theory and experiment.[4-8]To our knowledge, the values of the QZSC have been accurately measured,[9-14]but there is noab-initiocalculation on them until now. However,repeated determination ofC2is critical for precisely determining the second-order Zeeman shift and depressing its statistical uncertainty. On the other hand,accurately calculating the value ofC2can provide one of the most stringent tests of atomic structure calculations as it needs accurate atomic wavefunction.

In this work, we derived an expression of the QZSC of the3Po0clock state for88Sr and87Sr. It was found that the QZSC of the3Po0clock state for87Sr depends on the magnetic quantum numberMF. Using the multi-configuration Dirac-Hartree-Fock(MCDHF)theory,we systematically considered the electron correlations and Breit interaction effects and calculated the QZSCs. At the same time,the QZSCs of the3Po0,F=9/2,MF=±9/2 clock states were also measured in our87Sr optical lattice clock. We have found that there is an excellent agreement between the calculations and the measurements. As in Refs.[2,15],the1S0,F=9/2,MF=±5/2-3Po0,F=9/2,MF=±3/2 transitions were proposed as another clock transition for they are less sensitive to the magnetic field noise. Our calculations can be used for evaluating not only the second-order Zeeman shift of1S0,F=9/2,MF=±9/2-3Po0,F=9/2,MF=±9/2 transitions, but also the1S0,F=9/2,MF=±5/2-3Po0,F=9/2,MF=±3/2 transitions.

2. Theoretical method

2.1. Zeeman shift of fine-structure levels

In the presence of an external magnetic fieldB, the atomic Hamiltonian is[16]

whereαjandβjare the Dirac matrices,Σjis the relativistic spin-matrix andgs=2.00232 is theg-factor of the electron spin corrected by QED effects.

If we choose the direction of the magnetic field as the quantization axisz, only the magnetic quantum numberMJremains the good quantum number. The atomic states with the same magnetic quantum number and parity are mixed due to the magnetic interaction.[16]In the weak-magnetic-field approximation, according to the first-order perturbation theory,the atomic state wavefunction|Γ JMJ〉can be written as

2.2. Zeeman shift of hyperfine-structure levels

The Hamiltonian of an atom with nuclear spinI(/=0)can be expressed as

whereJ＇=J-1,J,J+1. From Eqs.(16)and(17),the magnetic matrix element between states with the sameFvalues depends onMF, while that with ΔF=1 depends on the absolute value ofMF. Therefore,the value of the QZSC isMFdependent.

2.3. MCDHF theory

In the framework of the MCDHF method,the atomic state function(ASF)Ψ(Γ PJMJ)is a linear combination of configuration state functions(CSFs)Φj(γjPJMJ)with same parityP,total angular momentumJand its component alongzdirectionMJ,that is,

whereP(r)andQ(r)are the radial wavefunctions. The coefficientscjand the radial functions are optimized simultaneously in the self-consistent field (SCF) procedure. Higherorder electron correlations, the Breit interaction and quantum electrodynamical(QED)corrections can be considered in the relativistic configuration interaction(RCI)computation,in which only the expansion coefficients are varied.

Our calculation was started in the Dirac-Hartree-Fock(DHF) approximation. The occupied orbitals in the reference configuration 1s22s22p63s23p63d104s24p65s5p,or called spectroscopic orbitals, were optimized and kept frozen in the following computations. The outermost 5s and 5p electrons were regarded as the valence orbitals and others as the core.In the following SCF calculations,the valence-valence(VV)and major core-valence(CV)electron correlations were taken into account.The major CV electron correlation includes those between electrons in the valence andn ≥3 core shells. The virtual orbitals were added layer by layer up ton=11 andl=4.

Keeping all orbitals frozen,we further considered the effect of the CV correlation related to then ≤2 electrons in the subsequent RCI computation. This model is labelled as CV.The core-core(CC)electron correlation in the 4s and 4p subshells,referred to as CC4,was also captured in RCI.To control the number of CSFs,only the first five layers of virtual orbitals were used to generate the CSFs accounting for the CC correlation. Higher-order correlations amongn ≥4 electrons was considered by the multi-reference (MR) single (S) and double(D)excitation approach. The MR configurations are composed of{4s24p65s5p, 4s24p64d5p, 4s24p65s6p, 4s24p65p6s,4s24p64d6p}. The corresponding configuration space was expanded by SD-excitation CSFs from the MR configuration set to the first five layers of virtual orbitals.Finally,the Breit interaction was evaluated based on the MR model. In practice,we employed the GRASP2K[18]and HFSZEEMAN[19]packages to perform the calculations.

3. Calculation results and discussion

In this work,our computational uncertainties mainly arise from the neglected CC and higher-order electron correlations related to then ≤3 core shells.These effects should be smaller than those from the outer shells because of the stronger nuclear Coulomb potential in the inner region. According to the cancelation between the CC and MR electron correlations in then=4, 5 shells, we speculated that there is also an offset between the neglected CC and its corresponding higher-order electron correlations. We estimated the contribution from then=3 CC correlation as 0.2%. This gives a rough uncertainty of 0.05 MHz/T2to the final value. Our calculated QZSCC2of the3Po0clock state for88Sr is in excellent agreement with the theoretical value given by Taichenachevet al.[23]and the experimental measurement given by Baillardet al.[24]

As mentioned above,the 5s5p3Po0clock state for87Sr has only one hyperfine stateF=9/2,and we can also treat the adjacent3Po1and1Po1states as perturbing states. For the two perturbing states, we analyzed the different hyperfine states contributions to the QZSC.The analyzed results are presented in Table 2. In this table,we presented all of theMF-dependent QZSCs of the3Po0clock state for87Sr. We can see that the value of QZSC decreases with the decrease of magnetic quantum numberMF.

Table 1. The ΔE(3Po0-3,1Po1), 〈3,1Po1‖N(1)+ΔN(1)‖3Po0〉 (all of them in atomic units), and the calculated QZSC C2 (in MHz/T2) of the 3Po0 clock state for 88Sr atom. Numbers in square brackets stand for the power of 10,and in parentheses for uncertainties.

Table 2. Contributions of different perturbing states to the MF-dependent QZSC C2 (in MHz/T2)of the 3Po0 clock state for 87Sr.

4. Experimental determination of the quadratic Zeeman shift coefficient

The schematic diagram of clock transition detection device of87Sr optical lattice clock is shown in Fig.1. After two stages of cooling, the cold atoms with a population of about 104are loaded into a horizontal one-dimensional optical lattice with a temperature of about 3µK.[25]The 813.42 nm lattice laser is stabilized to an ultra-low expansion(ULE)cavity with a finesse of 12000. The lifetime of the atoms trapped in lattice is about 3.6 s. The clock laser is locked to another ULE cavity with a finesse of 200000, by using the technology of Pound-Drever-Hall stabilization for repressing the frequency noise. The clock laser corresponds to the 5s21S0-5s5p3Po0transition atλ=698 nm. The clock laser is collimated with a beam waist of 2 mm by using a convex lens and overlapped with the lattice laser. The polarization of the clock laser is parallel with the lattice laser by adjusting the direction of a Glan-Taylor polarizer. Both the clock laser and the lattice laser are linearly polarized with the direction of the magnetic field and the gravity.second-order terms in B,the two clock transition frequencies are given by

The lattice tensor shift, which may deteriorate the measurement result,[12]is minimized by carefully aligning the polarization direction of the lattice and the clock lasers with the magnetic field quantization axis.

Fig.1. Schematic diagram of the optical lattice and clock transition detection of strontium optical lattice clock. C1: anti-Helmholtz coils,C2:three-dimensional compensating coils, TL: trapping laser, SL: string laser, PL: polarizing laser, LAL: lattice laser, CLL: clock laser, CL:convex lens with a focal length of 250 mm, CM: concave mirror, GP:Glan-Taylor polarizer of which the polarization axis is along the direction of gravity.

Fig. 2. Relationship between second-order Zeeman shift and effective magnetic field. The error bars indicate the purely statistical 1σ standard deviation given by the last point of the Allan deviation of selfcomparison. The solid line is the parabolic fitting curve with a function of a+b×B2eff.

In Table 3,we presented the comparison of the calculated and the measured QZSCC2of the3Po0,F=9/2,|MF|=9/2 states for87Sr. From the table,one can see that our calculated result is in good agreement with the measurements,especially the most recent measurement given by Bowdenet al.,[14]the uncertainty of which is about an order magnitude smaller than the other measurements. Our measured value is also consistent with the other measurements. This determined that our computational model is reasonable.

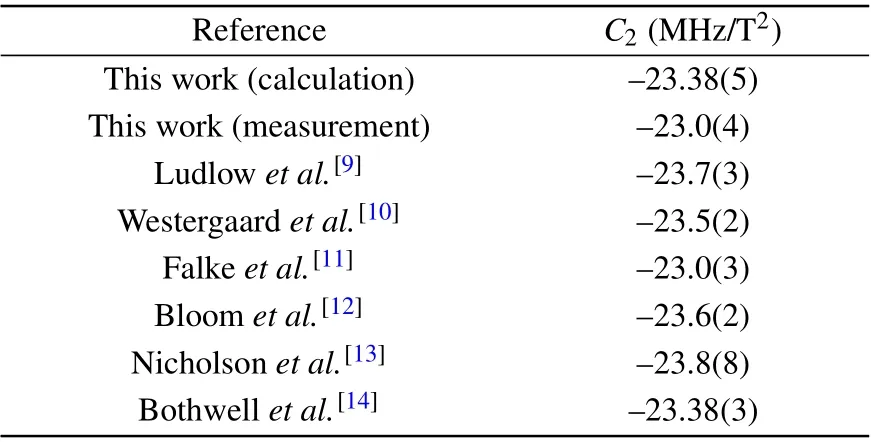
Table 3. The compassion of the calculated and the measured QZSC C2 (in MHz/T2)of the 3Po0,F =9/2,|MF|=9/2 states for 87Sr.

5. Conclusion

In the weak-magnetic-field approximation,we derived an expression of the QZSC of the3Po0clock state for88Sr and87Sr. It was found that the QZSC of the3Po0clock state for87Sr isMF-dependent. By using the MCDHF theory, we accurately calculated the QZSCs. In our calculations, the electron correlations and Breit interaction effects were systematically considered. At the same time, the QZSCs of the3Po0,F=9/2,MF=±9/2 clock states were also measured asC2=-23.0(4) MHz/T2in our87Sr optical lattice clock.Our measurements are consistent with the other experimental values. Moreover, we have found that there is an excellent agreement between the calculations and the measurements.Our calculations can be used for evaluating not only the second-order Zeeman shift of1S0,F=9/2,MF=±9/2-3Po0,F=9/2,MF=±9/2 transitions, but also the1S0,F=9/2,MF=±5/2-3Po0,F=9/2,MF=±3/2 transitions. The1S0,F=9/2,MF=±5/2-3Po0,F=9/2,MF=±3/2 transitions are the newly proposed clock transitions[2,15]for they are less sensitive to the magnetic field noise. Our theory is also useful to predict the QZSCs for other interesting atomic systems.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 61775220), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB21030100), the Key Research Project of Frontier Science of the Chinese Academy of Sciences(Grant No.QYZDB-SSW-JSC004),and the West Light Foundation of the Chinese Academy of Sciences (Grant No.XAB2018B17).