Protecting geometric quantum discord via partially collapsing measurements of two qubits in multiple bosonic reservoirs

Xue-Yun Bai(白雪云) and Su-Ying Zhang(张素英)

Institute of Theoretical Physics and State Key Laboratory of Quantum Optics and Quantum Optics Devices,Shanxi University,Taiyuan 030006,China

Keywords: geometric quantum discord (GQD), the Hilbert-Schmidt norm GQD, the trace norm GQD, partially collapsing measurements

1. Introduction

Quantum entanglement, the most common measure of quantum correlations, plays a vital role in the field of quantum information processing. For instance,it is widely used in the quantum computation,[1-4]quantum teleportation,[5]and quantum cryptography.[6]For many years, entanglement was considered as the only type of quantum correlations useful for quantum technology. However,it is gradually recognized that entanglement is not completely equivalent to quantum correlation,and some unentangled quantum states can still complete some quantum information processing tasks.[7]To characterize and quantify all of the nonclassical correlation contained in a given quantum state, quantum discord (QD)[8]as a new and the most popular correlation measurement has come into our view, which is defined as the difference between the total correlation and the locally accessible classical correlation.It has been shown that QD can be nonzero for some separable mixed states[9,10]and could be viewed as an invaluable resource of quantum computation and quantum communication.At present, QD has become a hot topic of special attention in the international academia,and many related theories[11-13]and experimental works[14-16]have emerged.

The QD plays a very important role in quantum computation,[17]local broadcasting,[18]remote state preparation,[19]thermodynamics of information,[20]quantum many-body systems,[21]and so on. However, only some special two-qubit states can obtain the exact analytical expression of QD, and the exact expression of QD for an arbitrary state of two qubits is unattainable.[22,23]So various types of alternative discord-like correlation quantifiers were introduced subsequently,[24,25]such as measurement-induced nonlocality(MIN),[26]geometric quantum discord(GQD),[27]measurement-induced disturbance(MID)[28]and global quantum discord,[29]etc. In 2010, Dakicet al. proposed the geometric quantum discord based on Hilbert-Schmidt norm(two-norm GQD),[27]and derived an explicit formula for measuring any two qubits. Although the two-norm GQD offers the advantage of easier computability, in view of two-norm GQD will increase the unmeasured part under the specific local operation, it is not the best way to measure the quantum correlation.[30-32]In order to avoid this problem, Paulaet al.proposed the geometric quantum discord based on trace norm(one-norm GQD)[33]in 2013,which can completely solve the problems of two-norm GQD.

Due to the ubiquitous environment,any quantum system is difficult to exist in isolation. It is of practical significance to analyze the QD behavior in open systems. Up to now, some achievements have been made in this respect.[34-48]For instance,Mohamedet al.[34]showed that there is no asymptotic decay for MIN while asymptotic decay exists for GQD, and the evolvement periods of GQD and MIN get shorter with the increase in the dipole-dipole interaction parameter, for a two-atom system in the non-degenerate two-photon Tavis-Cummings model. For the single sided and two-sided noisy channels,[35]even when the qubits are initially prepared in some mixed states, measurement-induced nonlocality can be expressed as the product of the initial measurement induced nonlocality and the channels’ action on the maximally entangled state. However, for the measurement-induced disturbance and quantum discord, there is no similar factorization law. Reference[37]illustrated that different initial states can be distinguished by using GQD,and the depolarizing channels heavily influence the dynamics of GQD and MIN as compared to the amplitude damping channel. Furthermore,no GQD and MIN sudden death is seen at finite temperature even in the presence of decoherence. Kenfacket al.[43]unveiled that the immunity of entanglement and QD against decoherence can be efficiently increased by properly adjusting the parameters of the input states,no matter the spectrum of the colored noise and the number of random bistable fluctuator (RBF) considered, and QD can be completely shielded from the decoherence by performing a weak measurement followed by its weak measurement reversal on the qubit of the system even when the decoherence process is strengthen with a large number of RBF affecting the qutrit. In the fidelity of teleportation and QD,the channel state are more stable and most efficiently under the influence of a dephasing environment than those under the influence of a dissipative or noisy environment.[47]

As is well known,the dynamics of a two-level open system weakly coupled to a single environment only exhibits Markovian behavior. However, it shows non-Markovian behavior even in the weak-coupling regimes if the system is coupled simultaneously to many environments. The consideration of simultaneous affections of multiple environments on a open system is relevant in many realistic situations, so it is necessary to understand the quantum dynamics problems in complex environment.[49-51]The geometric quantum discord dynamics of two-qubit states in this complex environment has not been studied so far. In this paper, based on the twoqubit systems interacting with their respectiveKindependent reservoirs of field modes,we discuss the effects of the qubitreservoir coupling and the number of reservoirs on two-norm GQD and one-norm GQD,and some meaningful conclusions are obtained.

The paper is structured as follows.We introduce the criterion for achieving the GQD of the Hilbert-Schmidt norm and the trace norm in Section 2. In Section 3, we give the model based on a two-level atom simultaneously interacting withKindependent reservoirs.Time evolution of two-norm GQD and one-norm GQD are investigated in Section 4. In Section 5,we investigate the protection of the GQD for entangled twoqubit systems by applying partially collapsing measurement.Finally,we conclude our work in Section 6.

2. Preliminaries

(A) The Hilbert-Schmidt norm geometric quantum discord(two-norm GQD).For a two-qubit systemρAB,two-norm GQD is defined as the minimal Hilbert-Schmidt distance between a state and the set of classical states,[27]namely,

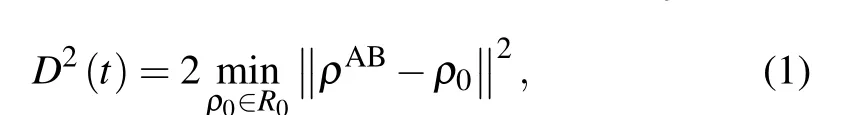
The value ofD1(t)is confined in the range 0≤D1(t)≤1,where the lower bound 0 indicatesρABbeing a classical quantum state and the upper bound 1 means the maximum quantum correlation.

3. Physical model and basic concepts

In this section,let us for concreteness consider a two-level atom with ground state|0〉and excited state|1〉simultaneously interacting withKindependent reservoirs of field modes. We assume all reservoirs initially in the vacuum and independent with each other. The Hamiltonian for the total system can be written as(with ¯h=1)[56]

To give the dynamics of these amplitudes in the interaction picture, we use the Schr¨oinger equation. Then we can obtain the following differential equations:

withυ=[Ce(t)]2. In the following, we display the dynamic evolution of both two-norm GQD and one-norm GQD for the two-qubit stateρAB(t).

4. Environmental effects on the two-norm GQD and one-norm GQD

The dynamical behaviors of the two-norm GQDD2(t)(red solid line) and the one-norm GQDD1(t) (blue dot line)are depicted in Fig. 1 for different number of reservoirsKin the weak coupling regimeγ=0.4λ. Here,K=1 indicates the qubit interacts with one reservoir, the weak system-reservoir coupling regime resulting in the system’s Markovian dynamics. In the presence of more than one reservoir, the system’s dynamics would becomes non-Markovian.D2(t)=D1(t)=1 atλt=0 implies that there is maximum quantum correlations at the initial time. From Fig.1(a),we can see that bothD2(t)andD1(t) decay monotonically with the dimensionless timeλtand suffers from a ‘sudden death (SD)’. This means that the local environmental noise leads to a decoherence effect onD2(t) andD1(t). When the reservoir numberKincreases to 3,D1(t)exhibits oscillatory behavior,which can be seen from Fig.1(b). WhenKincreases further(see Figs.1(c)and 1(d)),bothD2(t)andD1(t)become the oscillating functions of timeλt. At the same time,the oscillation frequency increases with the reservoir numberK.Insets in Figs.1(c)and 1(d)reflect the non-Markovian behaviors ofD2(t)andD1(t). The introduction ofKcan transform the Markovian dynamics to the non-Markovian dynamics. Furthermore, we can know thatD2(t)is always smaller thanD1(t)(except in the case of initial evolutionary time). Additionally,the death phenomenon ofD2(t)emerges earlier compared toD1(t).

The corresponding dynamic evolutions of the two-norm GQDD2(t) and the one-norm GQDD1(t) are presented in Fig.2 for the strong coupling regimeγ=4λ. In this regime,the quantum system can always exhibit the non-Markovian dynamics for anyK. In comparison with Fig. 1, both the frequency and amplitude ofD2(t)andD1(t)are larger with the same reservoir numberKin Fig.2. That is to say the largerKcan enhance the non-Markovianity of the overall environment.However,the survival time ofD2(t)andD1(t)is just the opposite,because the increase ofγresults in the information exchange between qubits and the reservoirs more frequently.

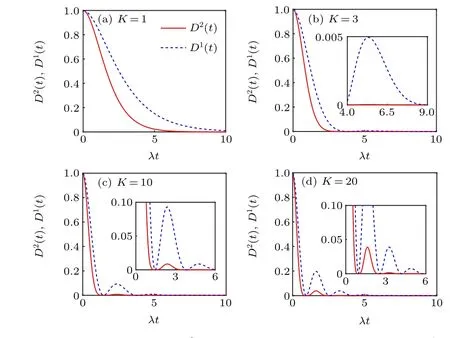
Fig.1. The two-norm GQD D2(t)(red solid line)and one-norm GQD D1(t)(blue dot line) as a function of dimensionless time λt in the weak coupling regime γ=0.4λ for K=1(a),K=3(b),K=10(c)and K=20(d),respectively.

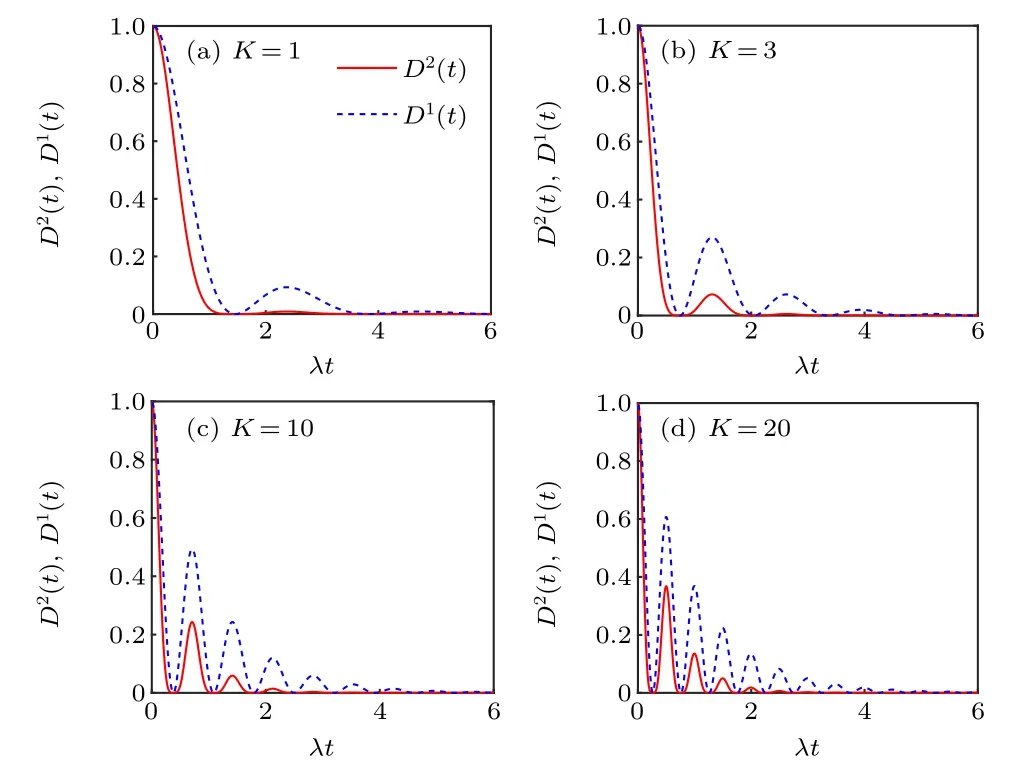
Fig.2. The two-norm GQD D2(t)(red solid line)and one-norm GQD D1(t)(blue dot line)as a function of dimensionless time λt in the strong coupling regime γ =4λ for K=1(a),K=3(b),K=10(c)and K=20(d),respectively.

5. Enhance the GQD with partially collapsing measurements

Quantum coherence plays an important role in quantum information processing,so it is urgent to protect quantum coherence from environmental effects. In recent years, various protection measures have been proposed, such as quantum Zeno effect,[58]decoherence-free subspace,[59]quantum error correction code,[60]and filtering operation.[61]Among which,the partially collapsing measurement method is one of the effective methods to protect the quantum coherence that has received much attention.[62]Partially collapsing measurement consists of quantum weak measurement (WM) and measurement reversal operation (WMR). For a single qubit, quantum weak measurement operationMwkand measurement inversion operationMrevin the standard basis{|1〉,|0〉}can be respectively written as

whereP= ˜ρ11(t)+ ˜ρ22(t)+ ˜ρ33(t)+ ˜ρ44(t) is the success probability. In the following, to gain the maximum quantum correction,we will choose the optimal measurement reversals strengthr=1-(1-m)|υ|.

In practice,the quantum state in a complex system,composed of two qubits and the multiple bosonic reservoirs,is affected by the parameterm. There is no initial correlation between the qubits A,B and the environment considered in this paper,but the correlation between qubits A,B and the environment will be redistributed in the course of time evolution. It is well known that the excitation of the system qubits is transferred to that of the environment qubits which causes decoherence,and the flow of information has an effect on quantum geometric discord.Here,Eqs.(21)and(23)respectively describe the reduced density matrix of qubits after tracing the environment without and with the partially collapsing measurements.Comparison of Eqs.(21)and(23)reveals the effect of the partially collapsing measurements on quantum state. The system qubits after the prior weak measurement has moved closer to the|00〉state that is less vulnerable to decoherence. A post measurement reversal operation with suitably chosen strength can make the system state close to the initial state. Thus the combination of these two operations will lead to the enhancement of GQD.

Fig.3. The dynamic evolutions of two-norm GQD D2(t)(red solid line)and the one-norm GQD D1(t)(blue dot line)under partially collapsing measurements with m=0.1 (upper panel) and m=0.3 (lower panel) in the weak coupling regime γ=0.4λ. The number of reservoirs K is K=3[(a),(c)]and K=10[(b),(d)],respectively.

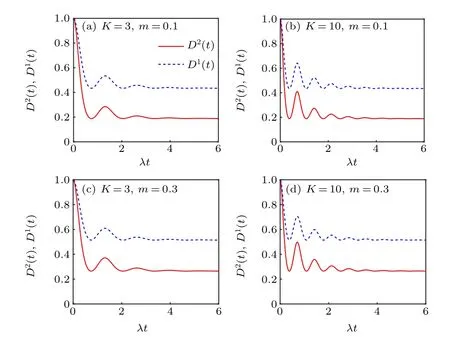
Fig.4. The dynamic evolutions of two-norm GQD D2(t)(red solid line)and the one-norm GQD D1(t)(blue dot line)under partially collapsing measurements with m=0.1 (upper panel) and m=0.3 (lower panel) in the strong coupling regime with γ =4λ. The number of reservoirs K is K=3[(a),(c)]and K=10[(b),(d)],respectively.

The dynamic evolutions of the two-norm GQDD2(t)(red solid line) and the one-norm GQDD1(t) (blue dot line) in the presence of partially collapsing measurements are plotted in Fig. 3 for the number of reservoirsK=3 (left panel) andK=10(right panel),in which Fig.3 corresponds to the weak coupling regime withγ=0.4λ. As depicted in Figs.3(a)and 3(b), for two different number of reservoirsK, after a finite time evolution,D2(t) andD1(t) can reach their own stable value with the same weak measurement strengthm=0.1. In other words,D2(t)andD1(t)can reach the stable value independent of the number of reservoirsK. Whenm=0.3 (see Figs. 3(c) and 3(d)), their final stable values ofD2(t) andD1(t) are larger than the casem= 0.1. The bigger stable value ofD2(t)andD1(t)can be obtained when the largermis given. Moreover, the stable value ofD2(t) is always smaller thanD1(t).

Next, we turn to investigate the effect of this measurements onD2(t) andD1(t) in the strong coupling regimeγ=4λ. Choosing the same system parameters as those in Fig. 3, we plot the numerical results for the dependence ofD2(t)andD1(t)onλtand with different weak measurement strengthmin Fig. 4. From these plots we can observe thatD2(t) andD1(t) achieve their own steady values in a finite time after several non-constant amplitude oscillations. We can find from Figs.3 and 4 that the final stable values ofD2(t)andD1(t)are independent of the parameterγ.

6. Conclusion

We useD2(t)andD1(t)as a combined tool to investigate the dynamics of quantum correlations in a two-qubit system with each qubit simultaneously interacting withKindependent reservoirs of field modes. We study the effects of the number of reservoirs on the dynamics ofD2(t) andD1(t) in detail. In the weak qubit-reservoirs coupling regimes,D2(t)andD1(t) asymptotically decay with the increasing time implying a Markovian dynamics when the number of reservoirsK=1. ThenD2(t) andD1(t) show non-constant amplitude oscillations whenK=10 and 20. The dynamic evolution ofD2(t)andD1(t)becomes non-monotonic signifying an emergence of the system’s non-Markovian dynamics. IncreasingKinduces an enhancement of memory effects,and causes the transition of the dynamics from Markovian to non-Markovian.In the strong qubit-reservoirs coupling regimes,D2(t) andD1(t) exhibit the oscillation behavior for anyK. There is an enhancement of the non-Markovianity by increasing the number of reservoirs. In addition,D2(t) andD1(t) tend to zero slower in the weak qubit-reservoirs coupling regime than in the strong qubit-reservoirs coupling regime. AndD2(t)is always smaller thanD1(t)except for the initial evolution time.We find that partially collapsing measurements can be used to protectD2(t) andD1(t) against the decoherence. When use the partially collapsing measurements,D2(t) andD1(t) can reach their own stable values independently of the parameterγand the number of reservoirsK. The study of partially collapsing measurements is rather significant in the course of quantum information processing.

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.11772177).