Post-solitons and electron vortices generated by femtosecond intense laser interacting with uniform near-critical-density plasmas

Dong-Ning Yue(岳东宁) Min Chen(陈民) Yao Zhao(赵耀) Pan-Fei Geng(耿盼飞)Xiao-Hui Yuan(远晓辉) Quan-Li Dong(董全力) Zheng-Ming Sheng(盛政明) and Jie Zhang(张杰)

1School of Sciences,Harbin Institute of Technology at Weihai,Weihai 264209,China

2Key Laboratory for Laser Plasmas(Ministry of Education),School of Physics and Astronomy,Shanghai Jiao Tong University,Shanghai 200240,China

3Collaborative Innovation Center of IFSA,Shanghai Jiao Tong University,Shanghai 200240,China

4Key Laboratory of High Power Laser and Physics,Shanghai Institute of Optics and Fine Mechanics,Chinese Academy of Sciences,Shanghai 201800,China

5Tsung-Dao Lee Institute,Shanghai 200240,China

Keywords: stimulated Raman side scattering,near-critical-density plasmas,electron vortices,post-solitons

1. Introduction

The femtosecond intense laser plasma interaction has brought a number of applications such as laser-driven particle acceleration,[1-4]high-order harmonic generation,[5,6]postsolitons and electron vortices generation,[7-10]and so on.These applications depend on laser-plasma parameters such as plasma density,laser polarization,and so on. For underdense plasmas,laser-driven wakefields[1]are widely used to electron acceleration and the following compact radiation source.[2]For solid density plasmas,laser-driven ion acceleration is suggested as a potential way for future cancer therapyucite.[11,12]And high-order harmonic generation (i.e., laser-driven attosecond sources) can be applied in materials science and molecular biology.[6]For near-critical-density (NCD) plasmas,nonlinear physical processes or structures like stimulated Raman scattering (SRS),[13]post-solitons[7,14]and electron vortices[9,10,15,16]have also been studied.However,the symbiotic relationships of these structures have not been explored in detail.Since the NCD targets are unique to many applications,such as fast ignition,[17]strong magnetic field generation[18]and magnetic vortex ion acceleration,[19,20]it is necessary to explore the generation and evolution of such nonlinear structures,and their symbiotic relationships. On the other side,the recent processes on the supersonic gas jet[21,22]and foam target manufacture[23,24]make the NCD targets available in experiments.

In this paper, by using multi-dimensional particle-in-cell(PIC) simulations, we study the transportation of ultra-short intense laser pulse in NCD plasmas. It is found that the laser pulse undergoes strong stimulated Raman side scattering(SRSS) and transverse hosing instability. At the same time,nonlinear structures such as post-solitons and electron vortices are excited. The generation of these structures depends on the drive pulse polarization. To study these effects, we first use S-and P-polarized laser pulses in two-dimensional(2D)simulations. For the S-polarized drive case, the SRSS processes develop due to the relativistic effect and then the scattered waves evolve into post-solitons. Both the main laser pulse and scattered waves can drive electron convection currents forming electron vortices due to the Kelvin-Helmholtz instability(KHI).While for the P-polarized drive case, the SRSS waves deposit their energy into plasmas by heating surrounding electrons. Strong transverse currents resulting from the laser acceleration along the polarization direction are observed and electron vortices are formed. In the three-dimensional (3D)simulation,we have observed different structures in the planes along and perpendicular to the polarized direction of the laser pulse,which are consistent with the simulation observation in the two-dimensional simulations.

2. Strong SRSS process during ultra-short intense laser propagation in NCD plasmas

The relativistic PIC code OSIRIS[25]has been used to perform multi-dimensional simulations. A linearly polarized laser pulse with wavelength ofλ0=1.0µm propagates along thexdirection. The peak intensity of the laser isI0=5.0×1019W/cm2corresponding to a normalized laser electric field ofa0=6.0. The pulse takes Gaussian profiles both in longitudinal and transverse directions with a duration of 20.0 fs and FWHM focus size of 6.0 µm. The simulation boxes are 110 µm×30 µm for 2D and 40 µm×30 µm×30 µm for 3D simulations which are divided into 2200×600 and 640×480×480 cells,respectively. A plasma with uniform density 0.2ncis placed atx ≥0.0µm,wherenc=1.1×1021cm-3forλ0=1.0µm. The ion mass is set to bemi=3672.0me,wheremerepresents the rest mass of electron.

2.1. The S-polarization case

Strong SRSS process has been observed when the ultrashort intense laser pulse propagates in NCD plasmas. In Fig. 1(a) one can see that a strong SRSS wave is generated from the tail of the drive pulse. For the SRSS process, the three-wave matching conditions for the wave vector and frequency need to be satisfied,i.e.,

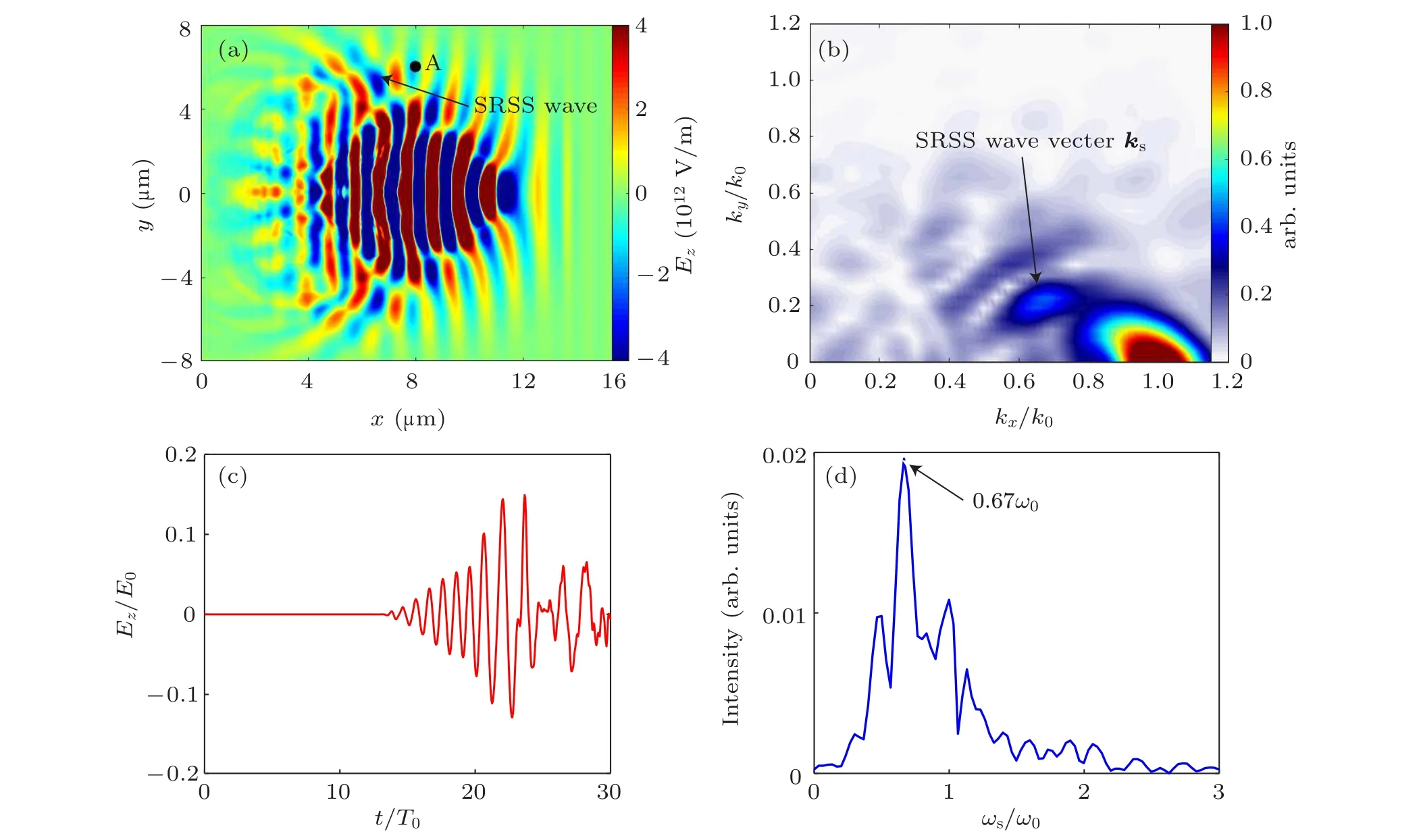
Fig.1. Distributions of laser electric field Ez in(a)spatial space(x,y)and(b)wave vector space(kx,ky)at t =20.0T0 for S-polarized laser case.(c) The temporal evolution of the normalized electric field Ez at point A in (a), where E0 =1.9×1013 V/m corresponding to a0 =6.0. (d) The SRSS frequency spectrum of Ez at point A in units of laser frequency ω0.

To analyze the SRSS process,we study the matching conditions and SRSS growth rate by considering the relativistic effects introduced by the drive laser. Distributions of the electric fieldEzin real space and in the wave vector space(kx,ky)are shown in Figs. 1(a) and 1(b). In Fig. 1(b), one can see that besides the main pulse, a strong SRSS wave with wave vector ofks=(0.62k,0.21k)appears att=20.0T0. The temporal evolution of this SRSS wave propagating through point A is shown in Fig.1(a). Its strength and spectrum are shown in Figs. 1(c) and 1(d). This SRSS wave is scattered by one of the plasma waves shown in Fig. 2(a). In Fig. 2(b), we show the corresponding wave vector of the plasma wave,i.e.,kp=(0.38k,-0.21k). The wavevector matching condition in Eq.(1)is satisfied for the three waves. A schematic view de-

For the SRSS waves, they are red-shifted and their frequencies go down when they propagate and dissipate energy.Eventually,they are captured by the surrounding plasmas and this results in the generation of post-solitons.[14]Such capture can happen outside of the plasma channel. We take the postsoliton in the dashed rectangle of Fig. 3(d) for an example.The post-soliton expands as a whole structure after the SRSS wave being captured which finally leaves an ion-bubble structure. With the post-soliton expanding, the frequency ofEzin it will be shifted to lower one[28]as shown in Fig.4(c).

Fig.2. Distributions of the longitudinal electric field Ex (i.e.,plasma waves)in(a)spatial space(x,y)and(b)wave vector space(kx,ky)at t =15.0T0.The schematics of SRSS physical process for an ultra-short intense laser pulse with(c)uniform intensity and(d)nonuniform intensity. Distributions of(e)electron density ne,(f)electron energy γe and(g)laser electric field Ez in spatial space(x,y)at t=15.0T0.

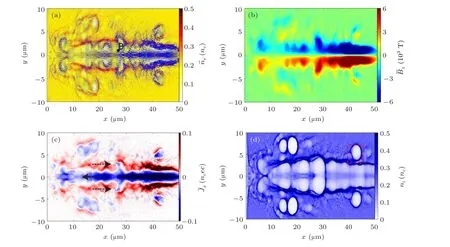
Fig. 3. Spatial distributions of (a) electric current vector and electron density ¯ne, (b) magnetic field ¯Bz, (c) longitudinal electric current density ¯Jx at t=70.0T0 and(d)ion density ni at t=140.0T0. The solid and dashed black arrows in(c)represent the drive current and the return current,respectively.The red dashed rectangle in(d)represents one example of post-solitons which is formed by the captured SRSS wave.

Fig.4. (a)The temporal evolution of the transverse current density Jy at point B in Fig.3(a). (b)The temporal evolution of the laser electric field Ez in post-soliton marked by the red dashed rectangle in Fig.3(d). (c)The corresponding frequency spectrum of Ez in the post-soliton.

2.2. The P-polarization case

For the P-polarized laser case, we observe similar SRSS process shown in Figs. 5(a) and 5(b). However, unlike the formation of post-solitons in the S-polarized case, the SRSS waves dissipate their energy quickly by heating electrons. As we show in Figs.5(c),6(b),and 6(d),the electrons around the main pulse are severely disturbed by the SRSS waves. Electrons can be repelled by the ponderomotive force of the main pulse to form an electron bubble as one can see in Figs. 6(b)and 6(d). The front of the electron bubble severely interacts with the main pulse and oscillates along the opposite of the polarized direction as one can see in Fig. 6. Such oscillation frequencyωLis proportional to the plasma density,[10]i.e.,ωL≈ω2p/ω0≈0.2ω0. As shown in Figs. 6(a) and 6(b),the laser pulse hoses downward which causes the charge separation field to deflect downward as marked by the blue arrow att=25.0T0. While att=28.0T0, the laser pulse hoses upward and causes the charge separation field to deflect upward as given in Figs. 6(c) and 6(d). Such hosing oscillation finally results in the production of a wave-like plasma channel as shown in Fig. 7(d). The oscillation amplitude is so large that the bubble deviates from the laser axis.

The hosing oscillation process also generates strong transverse currents on the two sides of the plasma channel.The couple between these adjacent transverse currents results in the two rows of electron vortices and associated magnetic islands as shown in Figs.7(a)and 7(b). The strong convective currents driven by the P-polarized pulse are also observed in Fig. 7(c). As one can see. the KH-type structures are found outside of the plasma channel which indicates that KHI may also play a role for the generation of such electron vortices.

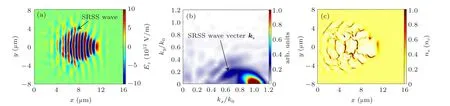
Fig.5. Distributions of laser electric field Ey in(a)spatial space(x,y)and(b)wave vector space(kx,ky)at t=20.0T0 for P-polarized case. (c)The distribution of electron density ne in spatial space(x,y)at t=20.0T0.

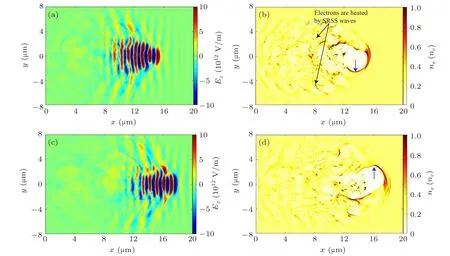
Fig. 6. The distributions of (a), (c) laser electric field Ey and (b), (d) electron density ne in spatial space (x,y) at (a), (b) t =25.0T0 and (b),(d)t=28.0T0. The blue arrows in(b)and(d)represent the transverse oscillating direction.

Fig. 7. Spatial distributions of (a) electron density ¯ne, (b) magnetic field ¯Bz, (c) longitudinal electric current density ¯Jx and (d) ion density ni at t=70.0T0.

3. Wave-like plasma channel, SRSS wave and electron vortices in 3D geometry

To further confirm the SRSS process and the generation of KH-type electron vortices in an ultra-short laser near-criticaldensity plasma interaction,we have performed a 3DPIC simulation. The laser pulse is linearly polarized along theydirection. The simulation results are given in Fig. 8. As one can see from Figs. 8(a) and 8(c), after the laser pulse leaves,a plasma channel with central current filament is left. Such current filament has been investigated for magnetic dipole vortex ion acceleration.[29]Associated with the current filament,magnetic dipole vortex vectors are plotted by the red cones in Fig. 8(a). In thexyplane (P-polarized plane), we observe a wave-like plasma channel caused by hosing oscillation,which is related to the polarization of the drive pulse. We also observe side channels driven by SRSS waves in thexzplane(Spolarized plane)as shown in Fig.8(b). Besides,compared to 2D geometry,the return current strength is generally weak due to dimensional effects as shown in Fig.8(c). However,the unstable condition of KHI can also be satisfied as long as the single shear flow is strong enough when the return current is negligible, i.e.,Γ2KHI=(kh·V1)2＞0. We can also observe the KH-type electron vortices induced by the KHI. Magnetic field associated with electron vortices, i.e., magnetic-islands structure,and one example of vortical current vector are plotted in Figs. 8(d) and 8(e), respectively. However, since the central axial current in the filament is so strong that it is hard to observe electron vortices induced by the hosing oscillation of the laser pulse. These characteristics are corresponding to the polarized planes as we found in 2D geometry.

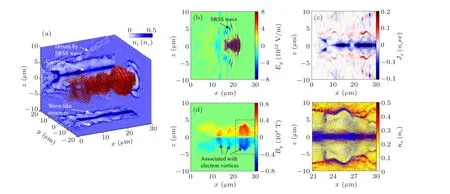
Fig. 8. (a) Spatial distribution of 3D plasma channel. Both xy and xz planes are cut right through the channel central axis, while the yz plane is corresponding to the slice at x=15.0 µm. Magnetic dipole vortex vectors are plotted by the red cones. Spatial distributions of (b) laser electric field Ey at t=30.0T0,(c)longitudinal current density Jx,(d)magnetic field By in xz plane at t=90.0T0. (e)Current vector of dashed red rectangle in(c)with electron density distribution as background at t=90.0T0. The linearly polarized drive pulse is polarized along the y direction.

4. Conclusion and perspectives

In conclusion, we have studied the transportation of an ultra-short intense laser pulse and the nonlinear structures generation in near-critical-density plasmas. Nonlinear processes including SRSS process with relativistic effect and nonlinear structures generation,like electron vortices and post-solitons,are numerically studied. In 2D simulations, we analyze the evolution relationships of SRSS process,electron vortices and post-solitons with S-polarized and P-polarized laser pulses respectively. The laser pulses undergo similar SRSS processes generating scattering waves both for S-polarized and P-polarized cases. However,for the S-polarized case,the frequencies of SRSS waves drop down when the scattering waves further propagate in the plasma. These waves are eventually captured by the surrounding cold plasmas and result in the generation of post-solitons with ion bubbles. While for the P-polarized case, the SRSS waves quickly dissipate energy by heating electrons around the main pulse. The main pulse can drive convective electric currents forming electron vortices in the plasma channel for both cases. However, the mechanisms for the generation of electron vortices are different in the two cases. The KHI is the main mechanism for the S-polarized case, while for the P-polarized case, the hosing oscillation of the laser pulse plays an important role for electron vortices generation. We have also performed a 3DPIC simulation to further verify the existence of KH-type electron vortices. Wave-like structure in the polarized plane and side channel driven by SRSS waves are also observed. Our findings are helpful for future relative experimental studies.

Acknowledgments

The authors would like to acknowledge the OSIRIS Consortium, consisting of UCLA and IST (Lisbon, Portugal) for the use of OSIRIS and the visXD framework.Project supported by the National Natural Science Foundation of China (Grant Nos. 11991074, 11774227, 12005287,and 12135009), NSAF of China (Grant No. U1930111), the Natural Science Foundation of Shandong Province, China(Grant No. ZR2019ZD44), and the Strategic Priority Research Program of Chinese Academy of Sciences (Grant Nos.XDA25000000 and XDA25050800).