Dynamics and intermittent stochastic stabilization of a rumor spreading model with guidance mechanism in heterogeneous network
2022-04-12XiaojingZhong钟晓静YukunYang杨宇琨RunqingMiao苗润青YuqingPeng彭雨晴andGuiyunLiu刘贵云
Xiaojing Zhong(钟晓静) Yukun Yang(杨宇琨) Runqing Miao(苗润青)Yuqing Peng(彭雨晴) and Guiyun Liu(刘贵云)
1School of Mechanical and Electrical Engineering,Guangzhou University,Guangzhou 510006,China
2College of Arts and Sciences,Beijing Normal University at Zhuhai,Zhuhai 519087,China
Keywords: guidance mechanism, heterogenous network, global dynamic analysis, aperiodically intermittent stochastic stabilization
1. Introduction
Rumor can be defined as a social phenomenon, which shows an unsubstantiated elaboration or interpretation of a thing, event or issue by using various means to attract public interest.[1,2]With the rapid development of internet technology and the widespread use of mobile network social platforms,such as Facebook, Twitter, Weibo and other social APPs, online social networks have replaced traditional communication means and become one of the most important ways to publish and disseminate information, while also contributes to rumor spreading.[3,4]Unfortunately, the prevalence of rumors may damage individual reputation,affect financial market and lead to social panic and instability.[5-7]Therefore, understanding the mechanisms of rumor propagation in complex networks is of great importance to supervise and control the rumor propagation.
Rumor propagation models have evolved from disease spreading models, such as SI, SIS, and SIR. Although the mechanisms of rumor propagation are similar to epidemic spreading, they are also fundamentally different. When a rumor spreader encounters another spreader,it may stop diffusing the rumor because they feel that people know about the rumor and lose interest. Researchers have established many rumor propagation models and proposed many useful analysis methods, mainly in homogenous networks and heterogeneous networks (Table 1).[8-18]In homogeneous networks,the node degrees concentrate around the mean-degree and follow Poisson degree distribution. Zanetteet al.[19]studied an epidemic like model for rumor propagation and put forward the critical threshold by mean-field approximation. In order to describe the internal relationship of the rumor spreading system, authors[9,10,16,17]established many double layer network models. Moreover,Danget al.[10,30]introduced counterattractors into category division. Tianet al.[13]considered debunking behavior in rumor spreading, and proved the stability of the rumor-demise equilibrium and the rumor-demise equilibrium. However,one disadvantage of homogeneous networks is its poor robustness. If a small number of nodes in the network are randomly removed, the whole network connectivity performance will be affected. For further addressing this problem, the heterogeneous networks has been proposed, where the node degrees obey power-law distribution and have scale-free property in most networks.[14,18,20-23]Considering the effect of people’s psychological factors like hesitation mechanism,[22]the forgetting and remembering mechanisms,[18]education mechanism,[13]cross-transmitted mechanism[23]and self-growth mechanism,[14]authors analyzed the reproduction theory and the global stability of rumor propagation equilibrium, and they found that the rumor spreads faster and the final size of the rumor is smaller in heterogeneous network. It is worth noting that the above researchers studies the rumor propagation behavior with deterministic model, i.e., fixed parameters. However, due to the various interior and exterior noises on the propagation process,different stochastic models have been considered,such as Itˆo stochastic models,[24-28]stratonovich stochastic models,[8]and Levy process models.[29]Authors proved the dynamic property around equilibriums and the existence of stationary distribution.
As well known, stochastic noises can stabilize unstable systems.[34-36]Even for epidemic systems[37,40]and malware propagation systems,[38]it has been proved that stochastic perturbations on contact rate and infections death rate can suppress the spreading of virus and malware. However, the positive effect of stochastic noises has not been explored in rumor propagation systems,especially the quantitative effect of stochastic noise on suppressing rumor propagation. Motivated by this, we propose a new rumor propagation model and design a new control method of a random noise stabilization.The main contributions can be summarized as follows.
Compared with the previous rumor propagation models,our new model considers the guidance mechanism and the heterogeneity in complex network. Our theoretical results prove that correct guidance measures can suppress the spread of rumor spreading.
The control strategy is a stochastic stabilization method driven by Brownian motion and the control time is aperiodically intermittent, which makes the control mode and control time more flexibility. We can choose a start time and a work width arbitrarily to balance the control requirement and the control cost.
The rest of the paper is organized as follows. In Section 2,we establish a new rumor propagation model,then we prove the global existence and the uniqueness of the positive solutions. Section 3 analyzes the global dynamics of the new rumor propagation model. IfR0<1,the rumor will die down naturally; and ifR0>1, the rumor will spread steadily to a certain scale. In Section 4,the stochastic stabilization strategy is designed and the control effect has been proven in details.In Section 5,numerical simulations are provided to verify our theoretical results. Section 6 gives the conclusion.
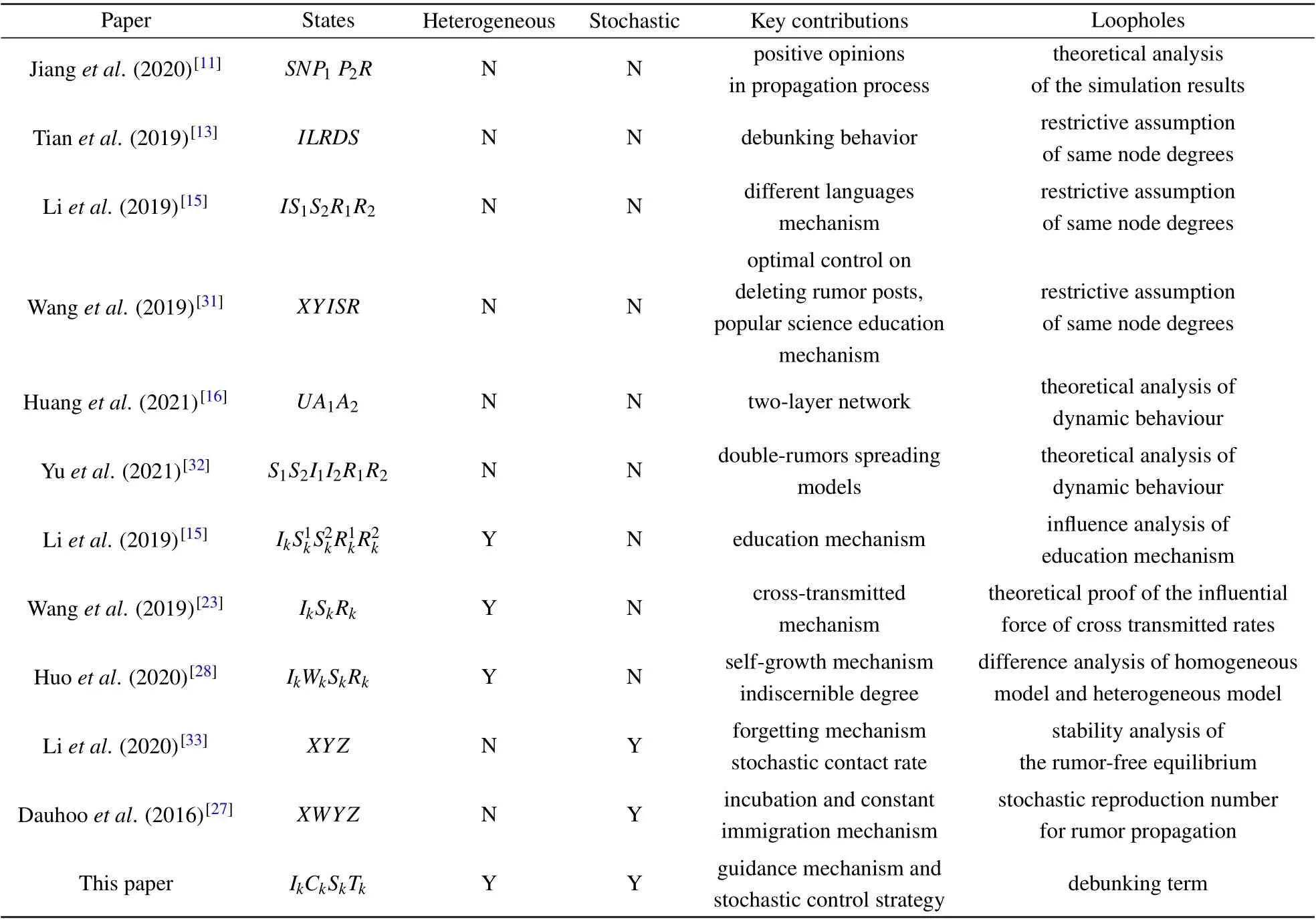
Table 1. Comparisons of some representative papers about rumor spreading.
2. Model formulation
In order to investigate the influence of rumor attraction on rumor spreading, we propose a heterogeneous ignoramuscommentators-spreaders-stiflers (ICST) model.N(t) denotes the size of whole individuals in heterogeneous networks at timet, which is divided into four categories: IgnoramusI(t),denoting individuals who do not know the rumor but vulnerable to affect;commentatorsC(t),representing individuals that comment the rumor if they contact with a rumor; spreadersS(t), denoting the rumor-propagating individuals whose behavior are believing and propagating after contacting with a rumor;and stiflersT(t),representing individuals that have no response to contact with a rumor. Considering the heterogeneity induced by different abilities of absorbing and disseminating information, the population is further divided into different categories by the connectivity degreekat timet, wherek=1,2,...,n. The topology structure of individuals in heterogeneous networks can be described in Fig.1. For simplicity,the rumor propagation model on heterogeneous network is named as the ICST model.The rumor propagation mechanism of the ICST model can be described as follows:
(R1)In a heterogeneous network, we assume that rumor propagate in a reasonable time,during which we can consider the number of immigrate individuals per unit of time as a constant related to degreek,named asbk. The emigration of each categories isµk.
(R2) When an ignorant individual contacts with a spreader, the ignorant may comment the rumor with probabilityαk,namely,the commenting rate;the ignoramus may be interested in the rumor and spreading the rumor with probabilityβk, namely, spreading rate; and the ignorant may have no response to the rumor with probabilityγk,namely,the stifling rate.
(R3)A comment individual has interest in the rumor,and he or she may become a spreader with probabilityηk. Before forwarding information, if he or she is guided to distinguish the truth with probabilityhk,then he or she may become a stifler with probabilityhkηk, or a spreader with probability(1-hk)ηk.
(R4)When a spreader contacts with another spreader,he or she could think the rumor has been propagated generally and becomes a stifler with probabilityδk.
Based on the above dynamics rules, we construct a transition diagram of the rumor spreading in Fig. 1. The rumor spreading model in the heterogeneous network can be expressed in the following equations:


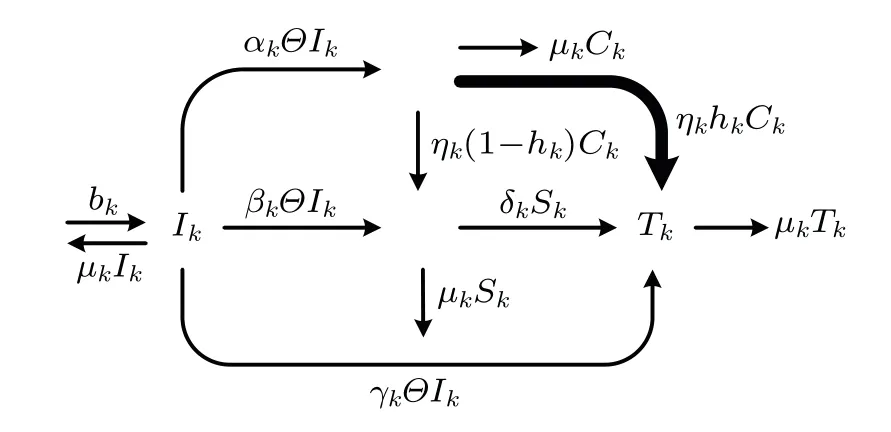
Fig. 1. Structure of rumor propagation under the influence of positive guidance from institutions or government department.

Table 2. Notations.
Remark 1 Compared with the work of[9,15], the guidance mechanism is introduced in the link from commentator to spreader, which invents guidance or education to the commentator by an organization or individual. A commentator will loss interest in a rumor by the man-made correctly guide,such as science refuting rumor, set forwarding permissions,etc. The guidance mechanism provides a new link from commentators to stiflers,and the number of spreaders will reduce subsequently. It should be stressed in particular that the guidance mechanism is different from the education mechanism in Ref. [9], which focused on the restraining of spreader. However,the guidance mechanism is targeted at commentator and the guidance rates are allowed to be different for different individuals.
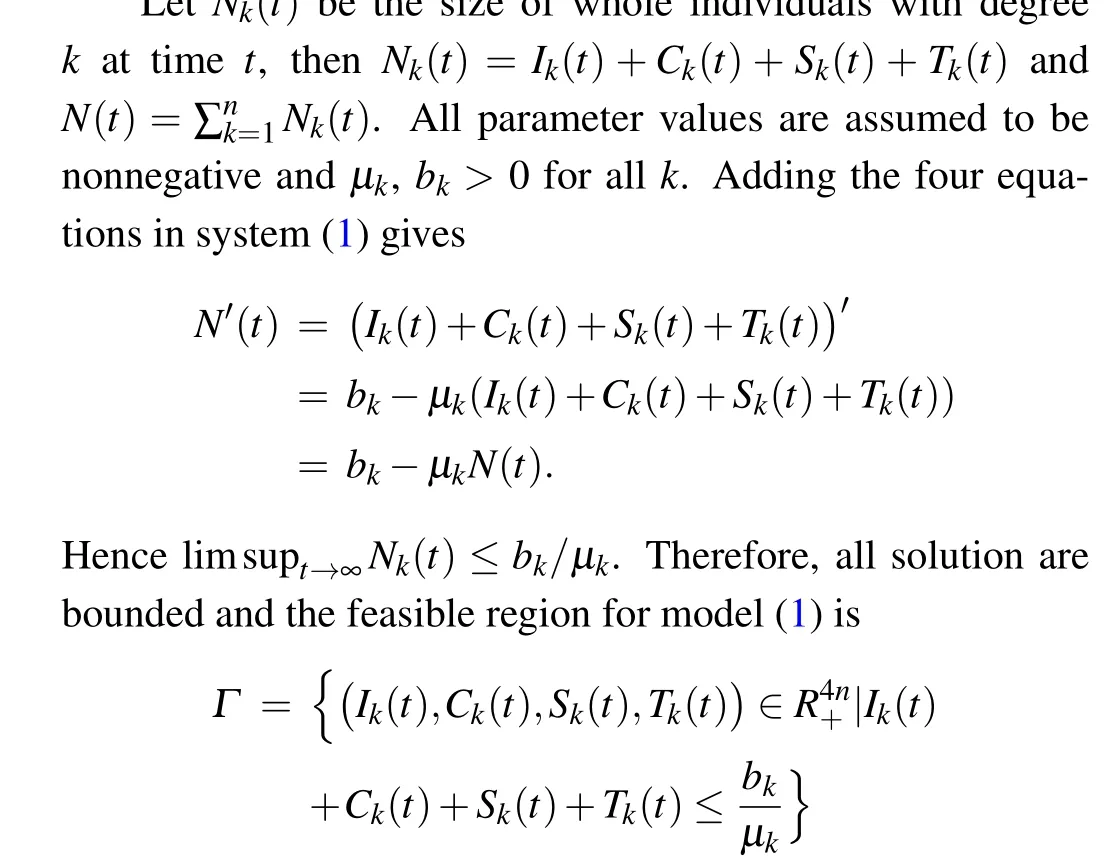
withk=1,...,n.
To guarantee the negativeness of the solutions of the new model(1),we make the following conclusion.
Theorem 1 For any initial valuesIk(0)>0,Ck(0)>0,Sk(0)>0 andTk(0)>0,k= 1,...,n, the solutions of the model(1)are positive for allt ≥0.
Proof For any given initial valuesIk(0)>0,Ck(0)>0,Sk(0)>0 andTk(0)>0,k= 1,...,n, we denoteX(t) =mint{Ik(t),Ck(t),Sk(t),Tk(t)}. Using reduction to absurdity,we assume there exists a constantτ >0,such that

a contradiction to ˙X(τ)≤0. Hence,Ck(t)>0,k=1,...,n.

3. Dynamic analysis of the deterministic ICST model
3.1. Equilibria and the basic reproduction number
In this section, we calculate a thresholdR0which determines the rumor dies out or out in nature,and prove the existence of a positive equilibrium underR0>1. Firstly, we calculate the equilibrium points of the deterministic ICST model.Letting the right side of model (1) equal to zero, we get the equilibrium equations as follows:


then we conclude that the rumor-prevailing equilibrium exists ifR∗>1.
Next, we calculate the thresholdR0. Based on the next generation matrix method, the propagation system can be divided intoFpart andVpart,which mean the rate of new infections to the compartment and the rate of transfer from the compartment,respectively. So we write system(2.1)as


3.2. Global dynamics when R0 ≤1


This implies that the largest invariant subset isE0. IfR0=1 andIk=bk/µk, by using the same argument as in the previous case,the largest invariant subset isE0as well. Therefore,all the limit points are contained in the largest invariant subsetE0. By the LaSalle’s invariance principle,E0is globally asymptotically stable ifR0<1.
IfR0>1, ˙V1>0,andE0is unstable. By the definition of the uniform persistence in Ref.[8],it is easy to check that the instability ofE0derives the uniform persistence of model(1).
Remark 2 Theorem 2 implies that the rumor naturally dies out from all stages and any size of the initial outbreak ifR0≤1. Otherwise the rumor persists at a constant state.Therefore,R0is a sharp threshold for the rumor persistence.
3.3. Global dynamics when R0 >1
As it is proved in Section 3.1, there is an informationprevailing equilibriumE∗ifR0>1. In this section,we show the global stability behavior of the equilibriumE∗by constructing a Lyapunov functions.[39]Generally,this implies the rumor persists at a unique scale even the initial size of information source is small.
Theorem 3 IfR0>1, then the information-prevailing equilibriumE∗is globally asymptotically stable inΓ.
Proof For convenient, we denoteSk(t)=Sk,Ck(t)=CkandIk(t)=Ik. The Lyapunov function for the related singlegroup model of system(1)can be constructed as follows:
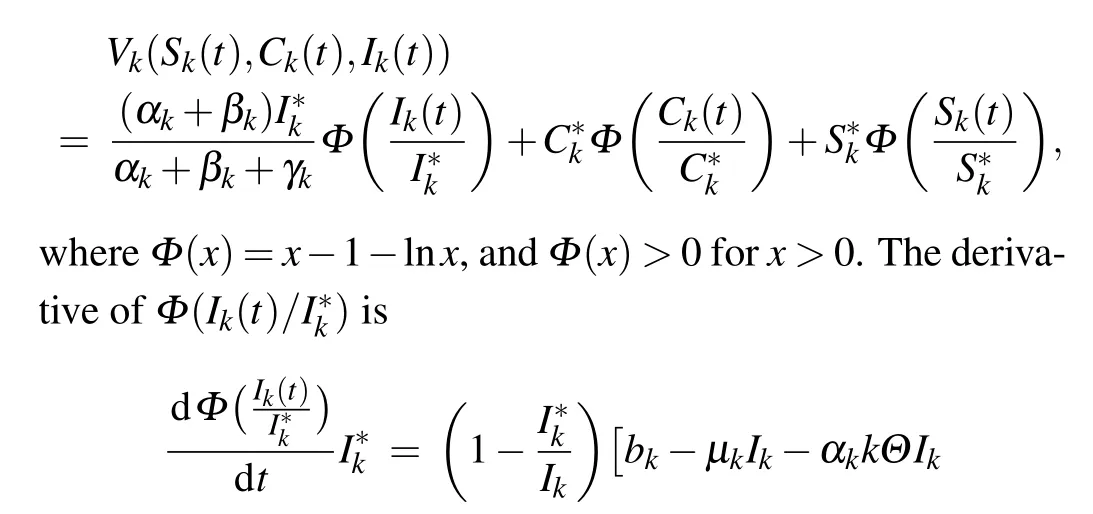

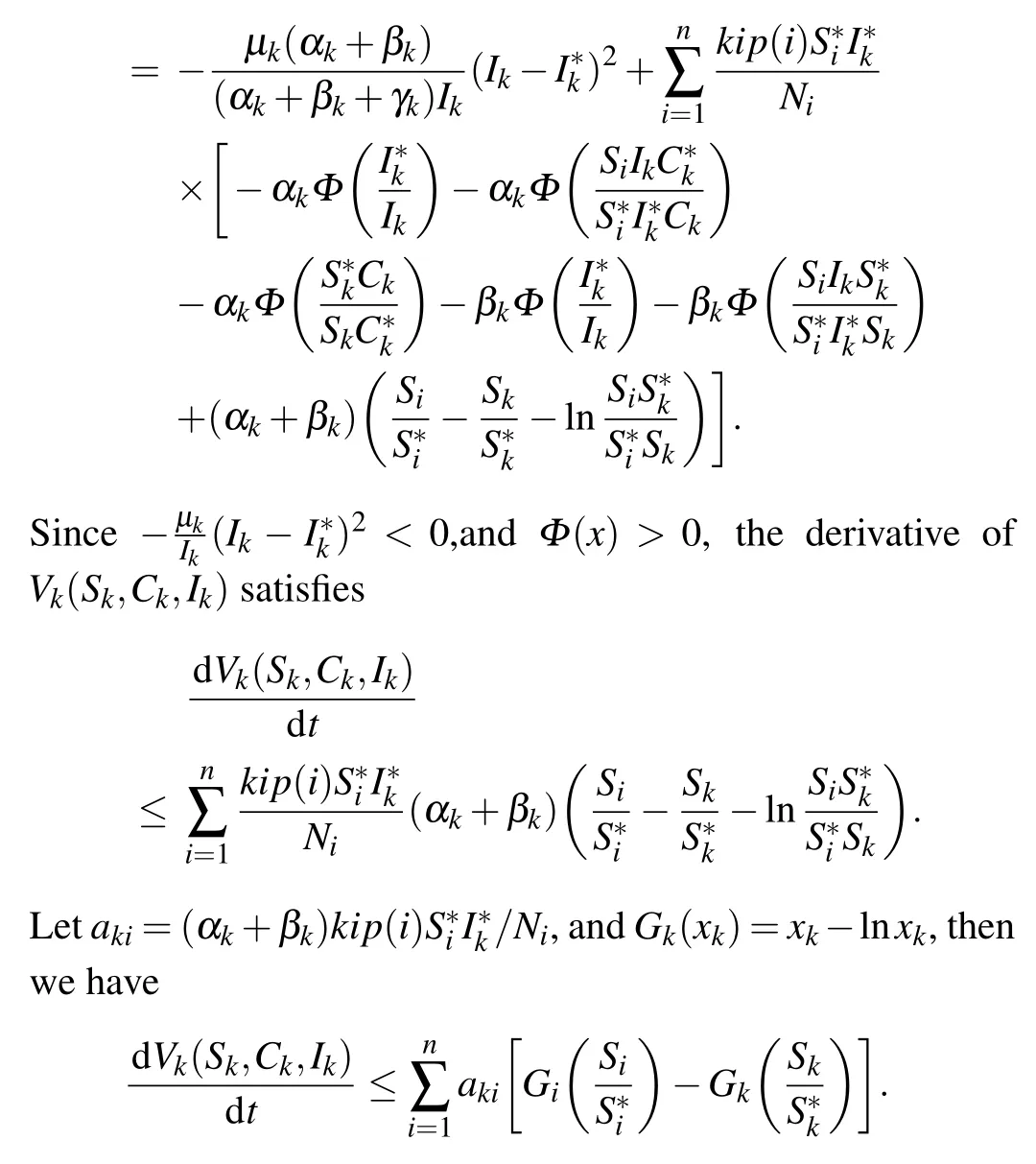
SoVk,Gkandakisatisfy the assumption of Theorem 3.1 and Corollary 3.3 by Li’s graph-theoretic method for Lyapunov functions.[39]Therefore, model(1)’s Lyapunov functions satisfy

Moreover, ˙Vk(Sk,Ck,Ik)=0 if and only if

By the LaSalle invariance principle,E∗is globally asymptotically stable.
4. Stochastic stabilization method on rumor propagation
Inspired by the favorable effects of white noise in epidemic system, we focus on the stochastic control strategy for rumor propagation in this section. The controller is made of the g-type white noise driven by Brownian motions. In particular,we design an intermittent time,aperiodic start and end points strategy to minimize the control cost and maximize the flexibility of control operation. Specifically, each time span[tk,tk+1) is divided into a work pattern [tk,tk+wk) and a rest pattern [tk+wk,tk+1), wherewkdenotes thek-th perturbed width which satisfies 0≤wk ≤tk+1-tk. The start timetkand the perturbed widthwkwould be different, and the total perturbed time ratiowsatisfies

Adding the g-type white noise to model (1), we get a new aperiodically intermittent stochastic perturbed system(AISPS)as follows:


for eachj ∈N.σrepresents the aperiodically intermittent perturb intensity. In the rest of this section, a stochastic stabilization criterion on rumor spreading of model (1) is established by Itˆo formula, exponential martingale inequality,Borel-Cantelli’s lemma and stochastic stabilization theory.


where



Remark 3 In the special caseti+1-ti=T,wi=δ,i=1,...,n, this method is equivalent to the periodically intermittent perturb method.[34]More specially, ifw=1, this method is a traditional stochastic stabilization method.[2]

5. Numerical examples
In this section,we conduct numerical simulations to illustrate the verification of the theoretical results and analyze how stochastic noises prevent the spreading process.
5.1. The simulation of rumor spreading process
Firstly,we discuss the effect ofµk,ηk,αk,βk,δkandhkonR0. By using the partial rank correlation coefficients(PRCCs)method,the key parameters for rumor spreading can be determined. The input parametersµk,ηk,αk,βk,δk, andhkare set to be uniformly distributed in Table 2, and we carry out 1000 runs to calculate multiple time points and plotted versus time. PRCCs plots of the basic reproduction numberR0and the scatter plot of six parameters are shown in Fig. 2. The contact rateβand the guidance ratehare strongly positive correlated toR0,and there is the negative correlation between emigration rateηandR0. It implies that guidance measure can effectively control the spread of rumors, and we suggest the government or the official should focus on interventions measures on emigration falls from commentator to spreader.

Fig.2. PRCCs of R0 of the ISCT model.

Table 3. PRCC values for R0.
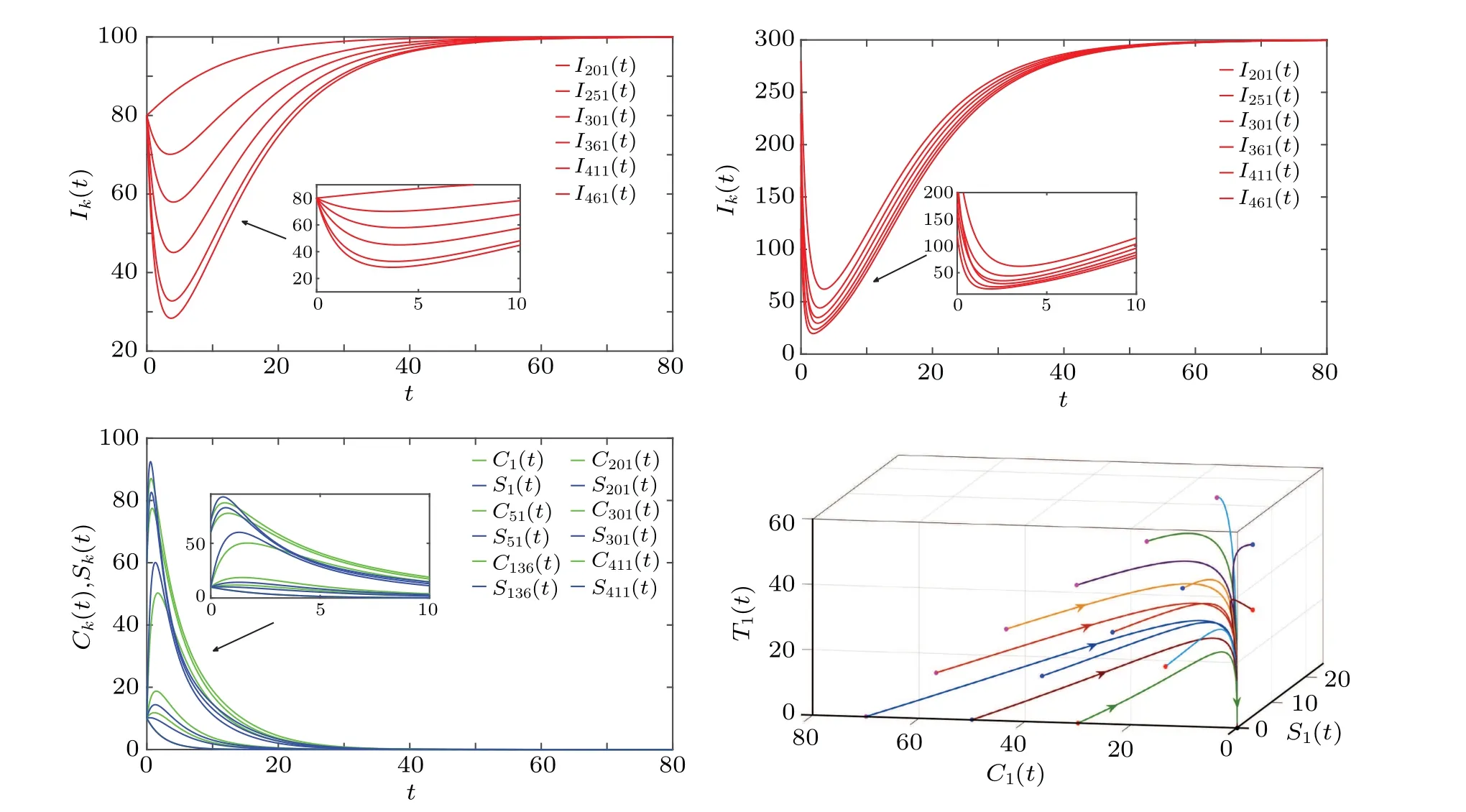
Fig.3. The stability of rumor-free equilibrium E0 with R0 <1.
Next,we concentrate on the test of global stability ofE0andE∗. The heterogeneous complex network is generated by using the scale-free network with the degree distributionp(k)=2m2k-3. We set the minimum degree of the network is 1,and the maximum degree is 500. Thus,the average degree of the network is〈k〉= 1.3688 by calculation. System parameters are summarized in Table 4,which fully consider the node degree difference as a result of parameter values. The initial values for 1≤k ≤200 areI0k=80,C0k=10,S0k=10,andI0k= 280,C0k= 10,S0k= 10 for 201≤k ≤500. If we choose the parameter values in column 1-2,one can calculate thatR0=0.1203<1,E0=(bk/µk,0,0),wherebk/µk=100 if 0≤k ≤200, andbk/µk=300 if 201≤k ≤500. Consequently,E0is globally asymptotically stable by Theorem 1.To verify the global property,the trajectories of(Ik,Ck,Sk,Tk)start at different initial conditions. We observe these trajectories tend to information-elimination steady statesE0under different initial points (see Fig. 3 and Table 5), which meansE0is globally asymptotically stable ifR0<1.
Using the parameter values in the second column of Table 4, one can calculate thatR0=1.4003,E0=(bk/µk,0,0),andbk/µk=100. From Theorem 1,E0is unstable, and the information-prevailing equilibriumE∗is globally asymptotically stable. To verify it,the trajectories of(Ik,Ck,Sk,Tk)start at eighteen different initial conditions. We observe these trajectories tend toE∗under different initial points(see Fig.4 and Table 6),which meansE∗is globally asymptotically stable ifR0>1.
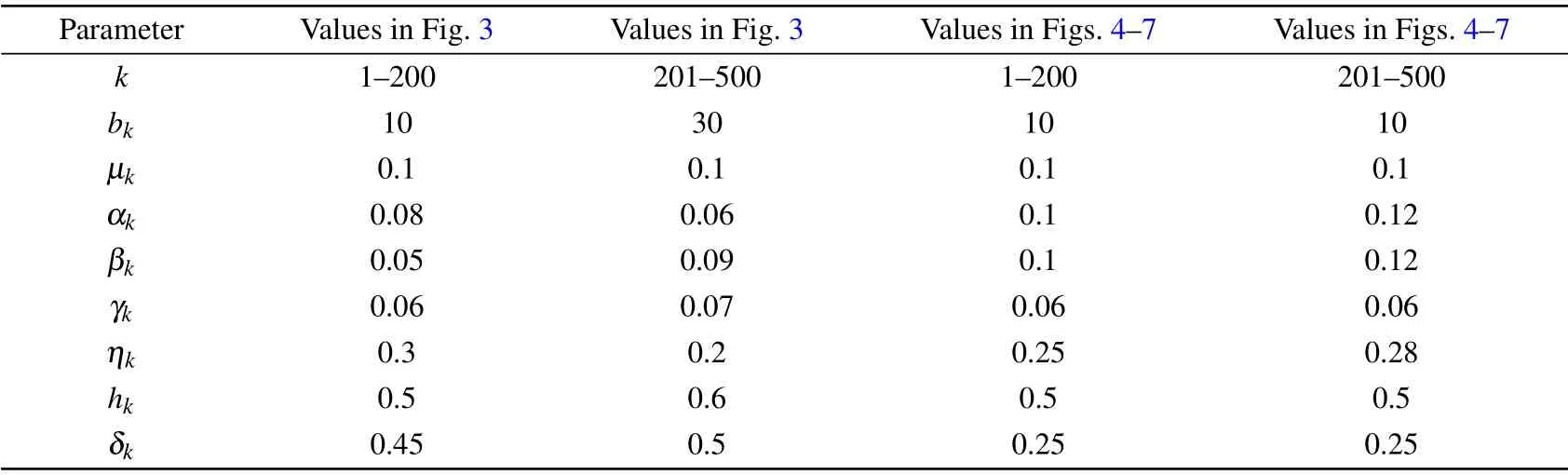
Table 4. Parameter values.

Fig.4. The stability of rumor-free equilibrium E0 with R0 >1.

Table 5. Numerical values at different time node degree under R0 <1.
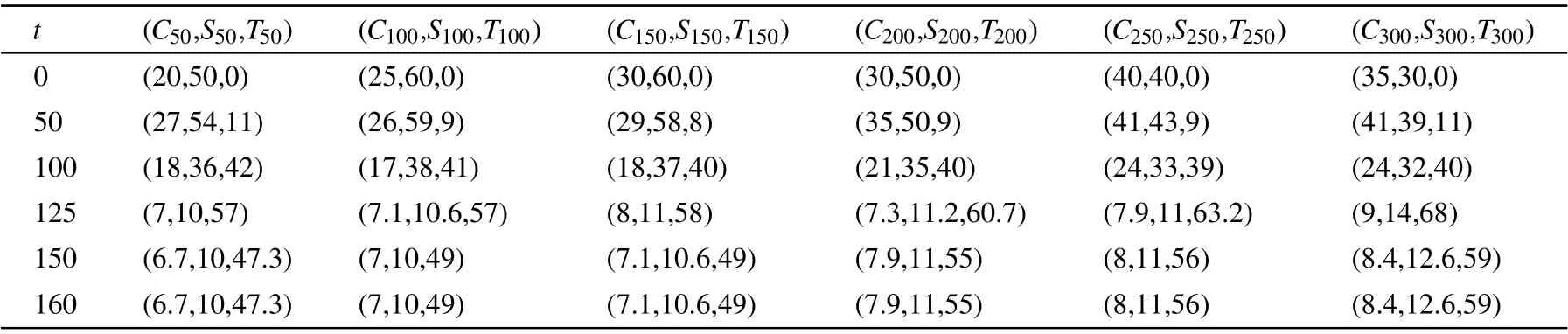
Table 6. Numerical values at different time node degree under R0 >1.
5.2. Effectiveness of the proposed stochastic stabilization method
To stabilize the rumor,we choose different control intensitiesσby adjusting control time to compare the stabilization effects(see Figs.5-7). We fix parameter values in the second column of Table 4. Ifσ=0, then rumor will propagate as shown in Fig.3. In order to check the effectiveness of the proposed stabilization strategy,we choose three groups of perturb intensity and the perturb time ratio to show the power of the proposed stochastic stabilization.
Firstly, assuming that the perturb intensityσ=0.8 and the perturb time ratiow=0.2, one can calculate thatσ2=0.64,and 2(δ+µ)(R0-1)/w=1.4. By Theorem 2,the perturb intensity is not enough to control rumor spreading,so the rumor will propagate in Fig.5.

Fig.5. Control ratio time w=0.2.
Secondly, we fix the perturb intensityσ=0.8, but increase the perturb time ratiow= 0.2 to 0.5. By calculation, the stabilization condition can be satisfied. The simulation result verifies our theoretical proof,and we observe that(Ik(t),Ck(t),Sk(t),Tk(t))converges toE0in Fig.6.
Finally, we increase the perturb time ratiowto 0.8 in Fig. 7, and observe that (Ik(t),Ck(t),Sk(t),Tk(t)) converges toE0faster than that forw=0.2(Fig.5)andw=0.2(Fig.6).So we can conclude that the proposed stochastic stabilization method can control the rumor propagation,and the bigger we apply the control intensity, the better control effect we have.Through above analysis,the optimal control strategy proposed in this paper is effective.

Fig.6. Influence of the control ratio time w=0.5 on convergence under two different intermittent strategies.
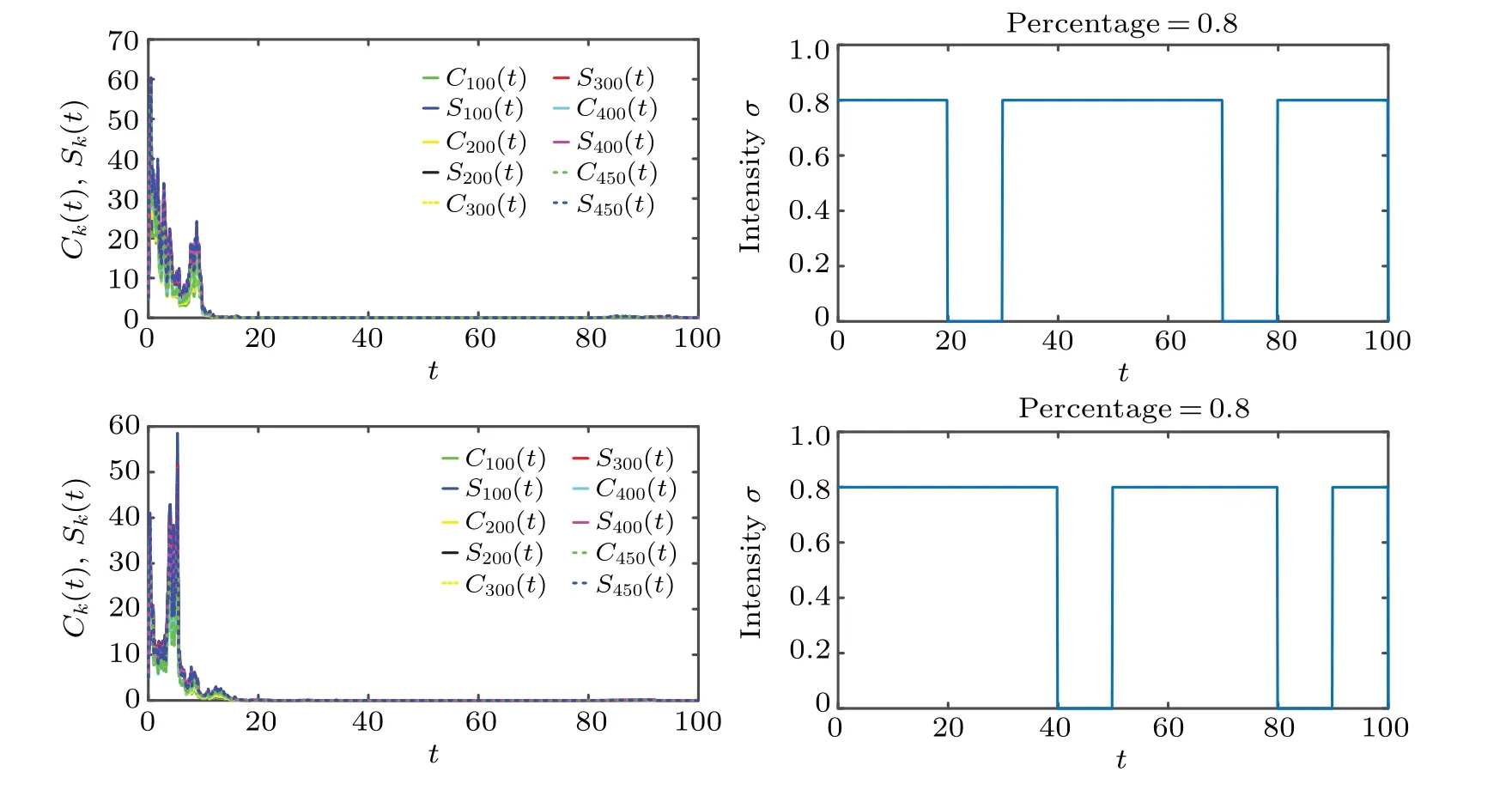
Fig.7. Influence of the control ratio time w=0.8 on convergence under two different intermittent strategies.
Remark 5 Figures 3 and 4 show the global stability ofE0andE∗. In actual situation,rumor management department can predict the rumor propagation trend by calculatingR0: IfR0<1, there is no need to add any extra control. IfR0>1,control strategy need to be carried out. Figure 5 shows the power of stochastic control strategy under different control intensity.In actual situation,rumor management department can block the information propagation channel randomly. For example,a rumor is expected to spread widely in Weibo,and rumor management department can randomly prevent some rumor spreader to spreading rumor,instead of prevent all spreaders.The speed of the control is decided by the control intensityσand the control time ratioτ.
6. Conclusions
In this paper, we propose a new ICST rumor propagation model that considers the social network connection heterogeneity and the guidance mechanism. According to the node degree,system parameters permit to be different,which is a generalization of Ref. [18]. Using the constructed mean field theory,we obtain the thresholdR0and equilibria. Global stability of the rumor-free equilibrium and rumor-prevailing equilibrium are also be proved by Lyapunov functions underR0≤0 andR0>1. Our studies show that the rumor threshold depends on the social network density and the guidance rate,and the positive guidance can reduce the rumor propagation force.
For rumor prevailing situation, we design an aperiodic intermittent stochastic controller to suppress rumor transmission. The expression of the minimum control intensity is calculated by Ito formula and exponential martingale inequality,which is inversely proportional to control time.It is highly recommended that control time and control intensity can be adjusted more flexibly to satisfy different control requirements.Our stochastic control method provides a new theoretical strategy for rumor propagation.
The simulation results show that rumor will naturally die out underR0≤0,regardless of initial points.When the thresholdR0>1,the rumor will prevalent in nature. But the rumor spreader can be stabilized to zero after an aperiodic intermittent noise controller,the greater the control intensity,the better the stabilization effect.
Acknowledgements
Project supported by the Guangzhou Science and Technology Project (Grant No. 20210202710) and Scientific Research Project of Guangzhou University (Grant No.YG2020010).
杂志排行
Chinese Physics B的其它文章
- Helium bubble formation and evolution in NiMo-Y2O3 alloy under He ion irradiation
- Spectroscopy and scattering matrices with nitrogen atom:Rydberg states and optical oscillator strengths
- Low-overhead fault-tolerant error correction scheme based on quantum stabilizer codes
- Transmembrane transport of multicomponent liposome-nanoparticles into giant vesicles
- Molecular dynamics simulations of A-DNA in bivalent metal ions salt solution
- Evaluation on performance of MM/PBSA in nucleic acid-protein systems
