Self-adaptive behavior of nunchakus-like tracer induced by active Brownian particles
2022-04-12YiQiXia夏益祺GuoQiangFeng冯国强andZhuangLinShen谌庄琳
Yi-Qi Xia(夏益祺) Guo-Qiang Feng(冯国强) and Zhuang-Lin Shen(谌庄琳)
1Department of Physics and Electronic Engineering,Yancheng Teachers University,Yancheng 224007,China
2Center for Soft Condensed Matter Physics&Interdisciplinary Research,School of Physical Science and Technology,Soochow University,Suzhou 215006,China
3Department of Chemistry and Environmental Engineering,Shenzhen University,Shenzhen 518060,China
Keywords: tracer,self-adaptive,super-diffusion,active Brownian particles
1. Introduction
Self-propulsion is a distinguishing feature of micro/nano swimmers such as bacterial, worm, artificial colloids.[1]Unlike passive systems in thermal equilibrium, self-propulsion allows active systems to display quite remarkable behaviors,including synchronous dynamics,[2]self-organization,[3,4]and unusual phase behavior.[5,6]Besides, the property of selfpropulsion, resulting from swimmers with the ability to take energy from their environment, also exerts a force on surroundings or obstacles.[7]For example,researchers have found that randomly moving bacteria can arouse a unidirectional rotation of asymmetric microscopic gears.[8,9]
Recently, the behaviors of microstructures[10]and polymers[11]immersed in active swimmers have received considerable attention. It has been found that swim pressure can give rise to the super-diffusion of wedge-like carriers, a tunable effective attraction between suspended rods,[12]and directed transport of chevron-shaped barrier.[10,13]Our previous work also has witnessed the incessant beating of brushlike structures,[14]globule-stretch transition of a collapsed chain,[15,16]and unidirectional rotation of a chain-grafted colloids[17,18]when mixing with the dilute active suspension.In addition, an effort has been made to steer the deformable microstructures by utilizing swimmers.[19]The shape of a vesicle oscillating from circle,to capsule and to dumbbell with the change of swimmer activity has been reported.[20]Intriguingly, Shanet al.[21]observed that these vesicles are packed into a loose network or porous structure with high motility in the phase-separation region, which provides a significant insight into the role of deformability in the assembly of microstructures induced by swimmers.
A rising interest in the field is designing microstructures to perform particular tasks such as energy harvesting and targeted delivery when immersed in an active medium.[22-24]Deformability may give rise to the advantages of self-adaptability as well as damage resistance. Inspired by the technological developments in the design and synthesis of artificial colloidal chains in experiment,[25]we design a nunchakus-like tracer and investigate its self-adaptive behavior in an active colloidal suspension via systematically tuning the self-propelled capability and density of colloids. Our results show that the nunchakus-like tracer will have a stable wedge-like shape in the active bath when the active force is high enough. We compute the angle between two arms of the tracer and the velocity of the joint point of the tracer. They all exhibit non-monotonic phenomenon as a function of active force.We also find a linear relationship between the velocity and the self-propelled force when the force is high enough. In other words,we also investigate the diffusion of the joint point of the tracer and find that the super-diffusive behavior can make the relation between the self-propelled force and density of active Brownian particles(ABPs)persist longer. In addition,we find that tracer can flip at high density of ABPs.
2. Model and methods
We consider a two-dimensional (2D) model where a nunchakus-like tracer is immersed in a suspension of selfpropelled colloids as shown in Fig. 1. The tracer is treated as two rigid chains(consisting of 19 beads)jointed by a flexible segment composed of three beads. The middle bead is seen as a joint point. We adopt the ABP model[26]to represent the self-propelled colloids. The self-propelled force of each ABP is directed along a predefined orientation, ˆni(θ)=(cosθ,sinθ),with a constant magnitudeFa. The overdamped Langevin equation is used to describe the motion of ABPs and beads of the tracer,

A purely repulsive Weeks-Chandler-Andersen potential(UWCA(r)) models all interactions among ABPs and tracer beads in the system,and is expressed as Eq.(4),in which cutoffrcis given as Eq. (5), withσbeing the diameter of each particle/bead andεthe interaction strength. The harmonic potential of successive beads on the chain isUs=ks(r-r0)2,whereksis the spring constant,ris the distance between the bonded beads, andr0is the equilibrium bond length. Here we setr0=0.98σandks=2500kBT/σ2, so that the chain is nearly inextensible to prevent active particles from crossing through it. Bending potential energyUb, which is responsive for the rigidity of chains,is written asUb=kb(θ-θ0)2,whereθis the angle between adjacent bonds,θ0=πis the equilibrium angle,andkb=10000kBT/σ2. The rigidity is turned off at the jointed point.
The home-modified LAMMPS software[27]is used to perform all simulations in a 2D periodic box withL=100σ.Reduced units are used in the simulations by settingσ=1 andkBT=1. The unit time isτ=1. And we setε=10kBTand the friction coefficientγ=10kBTτ/σ2. We treatDras a parameter independent ofDtas done in a previous work,[15]and setDr=1×10-3, so that the persistent time of ABP is long enough to manifest its self-propelled features. We tune the motility of ABPs by varying the amplitude of the propelled force,Fa(in units ofkBT/σ). All initial configurations are prepared atFa=0 via a long period simulation. Then each simulation is run for a minimum of 1×105τtime steps with each time step Δt=1×10-4τ.

Fig. 1. Schematic diagram of the system, consisting of a nunchakus-like tracer and active colloids. The tracer is modeled as two very rigid chains(orange) jointed by a flexible segment composed of three beads. The middle bead is defined as the joint point(purple). The colloid is represented by active Brownian particles (cyan) with the driving force along the inherent direction, ˆni(θ).
3. Results
This paper focuses on the following two questions: 1)how the tracer adjusts its shape in a suspension of swimmers and 2) how the activity and density of swimmers affect their behavior.
3.1. V-like shape formation
As an illustration of self-adaptability of the nunchakuslike tracer,we place it into a suspension of active colloids with packing fraction,φ=0.05 and swimmer self-propelled force,Fa=5. The time evolution of typical snapshots is shown in Fig. 2(a) (see supporting information, Movie1). We find that the tracer adjusts its conformation to adapt to the accumulation of ABPs and finally displays a V-like structure. The shape adjustment of the tracer at the beginning results from the persistent collision by ABPs.Then,the tracer locomotes,with the increasing assembly of ABPs caused by swimmer pressure.[28]The inhomogeneous aggregation of ABPs exerts a torsion on two rigid chains, promoting a V-like structure. On the other hand,the tendency of ABPs to accumulate at the place of large curvature,[29]namely the V region, forming a positive feedback in the deformation of the tracer. This behavior is vital for its locomotion and the sustentation of V-like structure.In order to verify that forming V-like structures is an adaptive behavior,we change the initial structure of the tracer. At the beginning of simulation, the two rigid chains have combined together(i.e.,fully folded up,which is possible when the tracer is hydrophobic tracer). We find that the tracer will still present the V-like structure(see supporting information,Movie2).
The evolution of the tracer shape can also be tracked by the angle,α, between two arms of the tracer. Theαis an intersection angle between two arms (Fig. 2(b)). Figure 2(b)shows that the angle decreases first with simulation time.Then it tends toward stability and finally fluctuates around 50°. The distribution ofαin the stable state is plotted in Fig.3(c). We find that theαyields the Gaussian distribution peaking at 50°with a variance of about 7°.
A typical trajectory for the joint point, to represent the mobility of the tracer, is shown in Fig. 2(d). Unlike the scenario of Brownian motion, the trajectory distinctly demonstrates a super-diffusive behavior. The supporting movie also manifests a net-directed motion of the tracer along the midline of two arms in the body-centered frame. We will discuss it below via mean square displacements(MSD),which shows that the tracer undergoes ballistic behavior for a short time. To describe the tracer motion,we also calculate its velocity for a short time,τ, and present thev=|Δr|/τin Fig. 2. We find that the velocity conforms to the Gaussian distribution with a mean value of 0.1σ/τ. The directed motion of the tracer benefits from the formation and maintenance of the V-like structure. From the supporting movie,we can see that the trapping of ABPs induces a high local density of active particles in the V region concerning the bulk,which will bring a non-zero net force directing from the concave side to the convex side. The mechanism is similar to the curvature induced activity.[10]
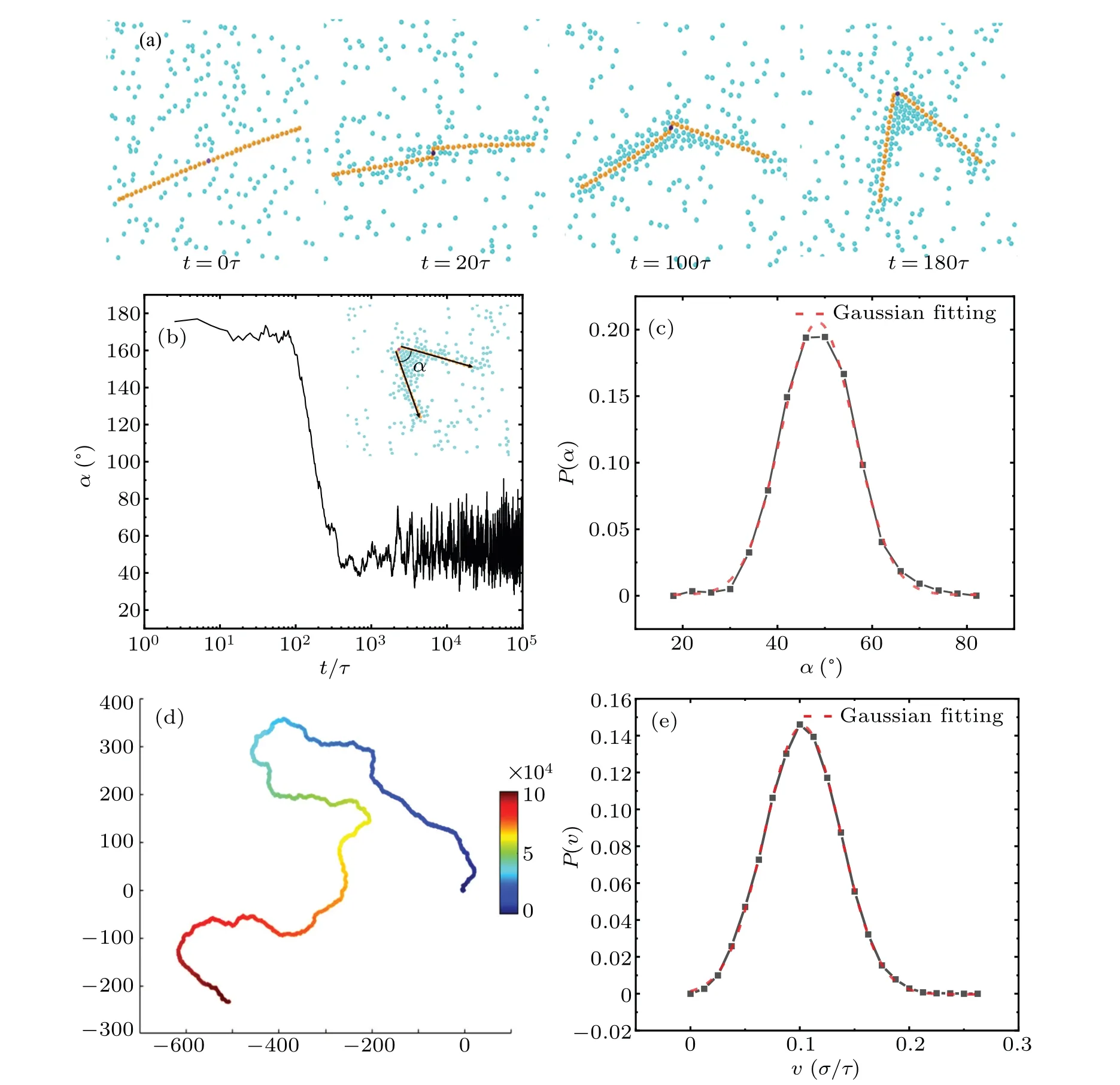
Fig.2. (a)Time sequence of typical snapshots for system with packing fraction of ABPs,φ=0.05 at Fa=5. (b)Time evolution of angle,α,between two arms of tracer,with inset denoting definition of α. (c)Distribution of α,(d)trajectory of tracer which is initially located at origin.Time that trajectory experiences is taken to be 105τ. (e)Distribution of velocity,v,of the joint point in the tracer,which is the average velocity of each τ.
3.2. Effect of propelled force
We use the average angle,〈α〉, to characterize the shape adjustment of the tracer affected by swimmer activity. Interestingly,〈α〉is non-monotonic with the increasing of selfpropelled force(Fig.3(a)). When swimmers are inactive,they are homogenous in bulk. The tracer behaves like Brownian motion in equilibrium. The depletion effect by ABPs is not strong enough to cause an attraction between two arms, possibly because the two arms are short. Thus〈α〉is large with a relatively large fluctuation. When theFais small, the collision frequency between ABPs and arms increases, and a small number of APBs become aggregated around two arms(Fig. 3(a)). The inhomogeneous pressure on arms resulting from the heterogeneity of local density yields a torque to reduce the〈α〉.AsFaincreases further,lots of ABPs are trapped into the V region (Fig. 3(a)), the steric interaction and growing pressure in the concave side induce the value of〈α〉to increase. Hence the angle between the two arms of the tracer adapts to the swimmer activity.
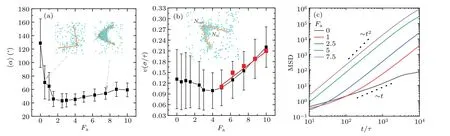
Fig.3. The Fa-dependent(a)average angle,〈α〉,between two arms of tracer,with insert showing two typical snapshots at Fa=0.5 and 7.5,and(b)velocity,v, of jointed point for the system with packing fraction, φ =0.05, with insert showing schematic for calculating Nin and Nout (c) log-log plots of the mean-square displacement(MSD)versus t/τ of the joint point of tracer with various swimmer activities,Fas. The standard errors are also shown.

Table 1. Statistics of〈Nin〉and〈Nout〉for various values of Fa.
Now, we come to investigate the mobility of tracer as a function of self-propelled force. The velocity of the jointed point, shown in Fig. 3(b), displays a similar behavior to the angle,with a non-monotonic change asFaincreases. It should be noted that the behavior depends on how to choose the time interval to calculate the average velocity. Here we useτas the time interval. At a small self-propelled force,the tracer seems to be in a thermal motion with a significant fluctuation of the average velocity. As the self-propelled force increases, a directed motion increases, and the velocity increases with the increase in swimmer activity. As shown in Fig. 3(b), the velocity monotonically increases whenFaexceeds 4.0.To understand the physical mechanism, we assume that the cluster of the tracer and surrounding ABPs moves directly under a large self-propelled force valueFaand build a simple theory based on the principle of force balance. On average,〈Nout〉beads assemble on the convex side, and〈Nin〉beads are trapped on the concave side (Fig. 3(b)). Both of them with various values ofFaare counted and given in Table 1. The total beads of the cluster are equal to〈N〉=〈Nout〉+〈Nin〉+Nrod, whereNrod=41 denotes the bead number of the tracer. The effective driving force giving rise to the direct motion results from the confrontation of swimmers inside and outside. Recalling deriving the settling velocity of a droplet,we have the equation
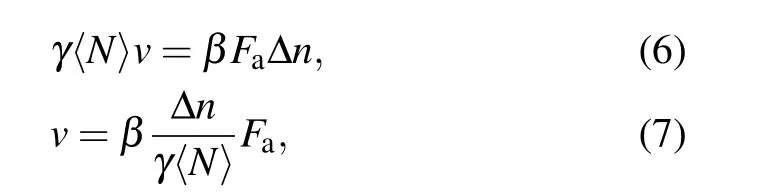
where Δn=〈Nin〉-〈Nout〉andβis a fitting parameter,which accounts for deviations due to simplification. As a result,we obtainvfrom Eq. (7). As shown in Fig. 3(b), by settingβ=0.98,the velocity is well obtained from this equation.
The typical MSD of the joint point to represent the dynamics of the tracer is shown in Fig. 3(c). AtFa= 0, the joint point undergoes sub-diffusive behavior possibly due to the topological restriction by two rigid arms. This behavior can also be seen on a short time scale for the small force case(Fa=1.0 and 2.5). This result indicates that the connection of two arms disturbs the normal Brownian motion of the joint point. On a long time scale, the joint point undergoes superdiffusive behavior atFa=1.0 and 2.5. When the active force exceeds 4.0, the motion of the joint point shows ballistic behavior in the time window of 104τ. In this case,the tracer can maintain a stable V-like shape and move directionally through the effective thrust exerted by the difference in density between internal and external particles.
3.3. Effect of ABP density
It is interesting to explore how the tracer adapts to the density of swimmers. To answer the question, we add ABPs into the system up to packing fractionφ=0.20, below the critical density for phase separation in bulk.[30]The〈α〉increases with packing fraction of swimmers increasing (see Fig.4(a)). The increase of density of ABPs leads more ABPs to be trapped in the V region, which is helpful in enhancing tha value of〈α〉due to the steric interaction. In addition, the tracer exhibits the ballistic behavior for a short time. However, the time scale for the tracer to cross a diffusive regime decreases as the density of ABPs increases(see Fig.4(b)).
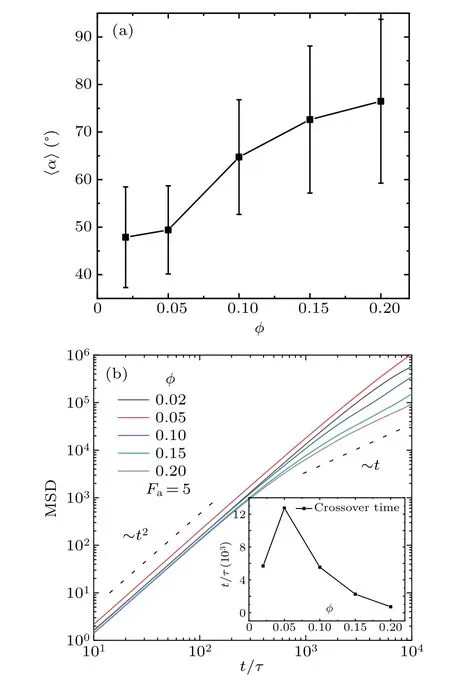
Fig.4. (a)Plot of mean angle, 〈α〉, between two arms of the tracer versus packing fraction, φ, of ABPs, and (b) log-log plots of MSD versus t/τ of joint point for various values of φ at Fa=5.
Also, a very low density of ABPs,φ=0.02, displays a small crossover time because the normal Brownian motion of the tracer plays a dominant role. The crossover time is determined by the rotational correlation time of the tracer.[16]At the very low density, trapped ABPs are less, which weakly suppresses the rotational Brownian motion of the tracer. On the contrary,high-density ABPs will assemble and encircle the tracer,which is detrimental to the directed motion. As shown in Fig.5, the instability of V-like shape occurs in the system.When the ABPs surround the tracer, the number of ABPs inside and outside the tracer becomes smaller. The mobility of the tracer lowers, and the swimmer pressure twists two arms due to rearrangement of ABPs.Then,two arms turn over to the reverse sides. It should be noted that the flip behavior of the tracer appears only in the high-density ABPs, in which there are enough ABPs to compass the tracer.

Fig. 5. Typical snapshots of flip behavior of tracer at packing fraction of ABPs,φ=0.20 and Fa=5.
4. Conclusions
In this work, we study the structure and dynamics of a nunchakus-like tracer in the bath of ABPs rough twodimensional Brownian dynamics simulation. Many experiments and simulations in soft matter systems, such as in suspensions of ABPs, use a passive tracer to investigate the dynamics of the complex system. Therefore, it is crucial to understand to what extent the dynamics of the tracers represent the fluid dynamics.In this paper it is found that the nunchakuslike tracer will have a stable wedge-like shape in the ABP bath when the self-propelled force is high enough. To explain the tracer’s degree of self-adaptation, we compute the angle between two arms of the tracer and the velocity of the joint point of the tracer. Both of them exhibit a non-monotonic phenomenon as a function of active force. However, the angle increases monotonically with density of ABPs increasing. A simple linear relationship between the velocity and the selfpropelled force is found in the highly active force.
The different activity and density of ABPs differ a lot in motion. If the tracer stays the wedge-like shape,the two arms of the tracer can drive enough ABPs inside the tracer into motion directly. (There is an effective propulsion along the direction from the center of mass to the joint point of tracer.)Therefore, the translational motion of the tracer is super-diffusive with high self-propelled force in a large time window. The density of the ABPs is another critical factor affecting diffusion. At the very low density, trapped ABPs are less, which weakly suppresses the directional motion of the tracer. On the contrary, high-density ABPs will assemble and encircle the tracer, which is detrimental to the directed motion. The super-diffusivity of these motions decays faster and recovers the normal diffusion in a short time window. In addition,this is also the answer to why tracer can flip at high-density ABPs.
We also consider the effects of some other parameters on the tracer in the supplementary materials. These parameters are rotation diffusion of ABPs,system size and the rigid chain length of the tracer. The angle and the velocity of the joint point of the tracer will decrease with the increase ofDr(see supporting information,Fig.S1). The angle of the tracer will increase with the box length increasing. However,the velocity of the joint point is unrelated to the box length(see supporting information, Fig.S2). The angle and the velocity of the joint point of the tracer will decrease with the rigid chain length increasing(see supporting information,Fig.S3).
The hydrodynamic interactions (HIs) are ignored in our model, which significantly affect the dynamics. Because the presence of substrates or confinement suppresses the longrange HIs in the quasi-2D system,our results can also be tested in a macroscopic granular experiment in which HIs are no longer a problem.
In addition,efforts are made to understand the dynamics,phase separation behavior,and self-assembly characteristics of deformable or irregularly shaped active particle suspensions.An emerging direction in this field is to design microstructures to perform specific tasks, most notably when immersed in the active particle bath,[22]which drives tiny gears or motors to capture the active particles. Besides, the active particles are used to push wedge-shaped carriers.[23]Compared with previous models, our model is very intelligent as a particle collecting machine. The geometry of microdevice is a critical ingredient that effectively converts energy from nonequilibrium environments into mechanical work. According to the self-adptive behavior of the model,the microdevices can be designed,which are used to determine the local direction of a fluid in the future.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos. 11804085 and 21674078), the Natural Science Foundation of the Jiangsu Provincial Higher Education Institutions,China(Grant No.21KJB140023),and the Foundation of Jiangsu Provincial Innovation and Entrepreneurship Doctor,China(Grant No.JSSCBS20211147).
杂志排行
Chinese Physics B的其它文章
- Quantum walk search algorithm for multi-objective searching with iteration auto-controlling on hypercube
- Protecting geometric quantum discord via partially collapsing measurements of two qubits in multiple bosonic reservoirs
- Manipulating vortices in F =2 Bose-Einstein condensates through magnetic field and spin-orbit coupling
- Beating standard quantum limit via two-axis magnetic susceptibility measurement
- Neural-mechanism-driven image block encryption algorithm incorporating a hyperchaotic system and cloud model
- Anti-function solution of uniaxial anisotropic Stoner-Wohlfarth model
