Deterministic remote state preparation of arbitrary three-qubit state through noisy cluster-GHZ channel
2022-04-12ZhihangXu许智航YuzhenWei魏玉震CongJiang江聪andMinJiang姜敏
Zhihang Xu(许智航) Yuzhen Wei(魏玉震) Cong Jiang(江聪) and Min Jiang(姜敏)
1School of Electronics&Information Engineering,Soochow University,Suzhou 215006,China 2School of Information Engineering,Huzhou University,Huzhou 313000,China
Keywords: deterministic remote state preparation,arbitrary three-qubit state,cluster state,quantum noises
1. Introduction
As a fundamental property of quantum mechanics,quantum entanglement has led to many important discoveries,such as quantum teleportation (QT),[1-3]quantum key distribution (QKD),[4,5]quantum secret sharing,[6]quantum dialogue,[7]quantum dense coding,[8]and remote state preparation (RSP).[9,10]Compared with their classic methods, in principle, quantum protocols can guarantee a higher security.Research in the fields of quantum system control[11-16]and quantum information processing[17-20]have been extensively studied in recent years. The idea of QT was first proposed by Bennetet al.[1]in 1993,in which the sender wished to transmit an arbitrary single-qubit state to a distant receiver via the maximally entangled Bell state.Neither the sender nor the receiver knows any information about the state to be transmitted.Later,the concept of remote state preparation was proposed by Loet al.[9]in 2000, where the sender could remotely prepare an arbitrary single-qubit state for the receiver by classical communication and a pre-shared entangled state. Different from QT, the sender prepares a known state for the receiver with a pre-shared quantum channel and appropriate measurements.Until now,there are already many different kinds of RSP protocols reported,such as deterministic RSP(DRSP),[21,22]joint RSP(JRSP)[23,24]and controlled RSP(CRSP).[25,26]The main advantage of DRSP over RSP protocol is that DRSP protocols can guarantee unit success probability. Various DRSP protocols have been proposed over the past few years and many entangled states(e.g.,Einstein-Podolsky-Rosen(EPR)pairs,[27-30]GHZ state,[31,32]cluster state,[33,34]χstate,[22]Brown state[35]and Bell state[36]) have been used to implement DRSP.In 2013,Zhanet al.[37]proposed a DRSP scheme by using six EPR pairs, where a four-qubit cluster state was remotely prepared. In 2015, Houet al.[38]presented several DRSP schemes of four-qubit W state via EPR pairs and GHZ states. In 2017,Zhanget al.[22]and Maet al.[23]put forward two DRSP protocols, in which arbitrary two- and three-qubit states were prepared by takingχstate and Brown state as the entangled channels. In 2018, Weiet al.[39]gave an efficient DRSP scheme for preparing an arbitraryn-qubit equatorial state via multiple two-qubit maximally entangled states. In 2020, Zhaet al.[40]proposed two DRSP protocols, where an arbitrary four-qubit cluster state could be prepared using two Bell states. In these schemes, the ideal channels were used.However,noises inevitably influence the process of the quantum information transmission.
Recently,researchers have examined the effects of quantum noise on DRSP of one-qubit,[41]two-qubit[42,43]and three-qubit[44,45]states. In 2019, Zhanget al.[42]proposed two DRSP schemes of arbitrary two-qubit state via theχstate channel in noisy environment. In 2020, Qianet al.[41]presented a DRSP scheme, in which arbitrary one-qubit state working in noisy environment was prepared via one intermediate node. Dashet al.[43]investigated the effects of different quantum noises on DRSP of arbitrary two-qubit system.The effects of quantum noise have been taken into consideration in these DRSP schemes. There have been many studies previously published on the RSP of arbitrary three-qubit state.[44-47]In 2016,Falayeet al.[44]put forward a JRSP protocol of three-qubit states via three tripartite GHZ entangled states in noisy quantum channel,by putting some special cases into consideration, in which the success probability could be ameliorated to 1. In 2018,Sunet al.[45]studied the effects of noise on two DRSP protocols of an arbitrary three-qubit state,whereχstate and Brown state were used as the quantum channel,respectively.
Cluster states have played a crucial role in quantum information processing tasks in recent years. It is worth noting that there has been no study on the DRSP of three-qubit states when the cluster-GHZ channel are used so far. Here,we present a deterministic remote state preparation protocol for remotely preparing arbitrary three-qubit state in ideal environment,where the sender Alice and the receiver Bob share a composite cluster-GHZ state as the quantum channel. Alice performs two three-qubit measurements based on her knowledge of the original states. Finally,according to Alice’s measurement results,the receiver Bob can reconstruct the respective target state by preforming appropriate unitary operations.In this paper,we also analyze the impact of four kinds of quantum noises, such as amplitude-damping, phase-damping, bitflip and phase-flip noises,on DRSP of an arbitrary three-qubit state via a nine-qubit cluster-GHZ state channel. Further, we provide the fidelity results of arbitrary three-qubit target state.The results of this study indicate that the fidelities depend on the noise parameters,the amplitude parameters and the phase information of the initial state. The detailed analysis will be given in Section 3. The structure of the paper is arranged as follows. In Section 2,we introduce a novel DRSP protocol of arbitrary three-qubit state via a nine-qubit cluster-GHZ state channel. In Section 3,we proceed to investigate the effects of noises on the quantum channel and analyze the fidelities obtained. Finally,we discuss the performance of our scheme and close the paper with a brief summary in Section 4.
2. Remote state preparation of an arbitrary three qubit state
In this section,we discuss the remote state preparation of an arbitrary three-qubit state under ideal channels. Suppose that there are two participants: Alice and Bob. Alice intends to prepare an arbitrary three-qubit state for Bob. Here the state is known by Alice. The receiver does not have any knowledge about the original state at all. The desired state is described as follows:

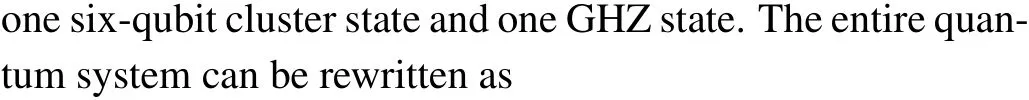

Here, qubitsa1,a2,a3,a4,a5anda6belong to Alice andb1,b2andb3belong to Bob,respectively.
In order to realize the DRSP of arbitrary three-qubit state for Bob, Alice firstly performs a projective measurement on her particles with the mutually orthogonal base{|φi〉}(i=0,1,2,...,7):
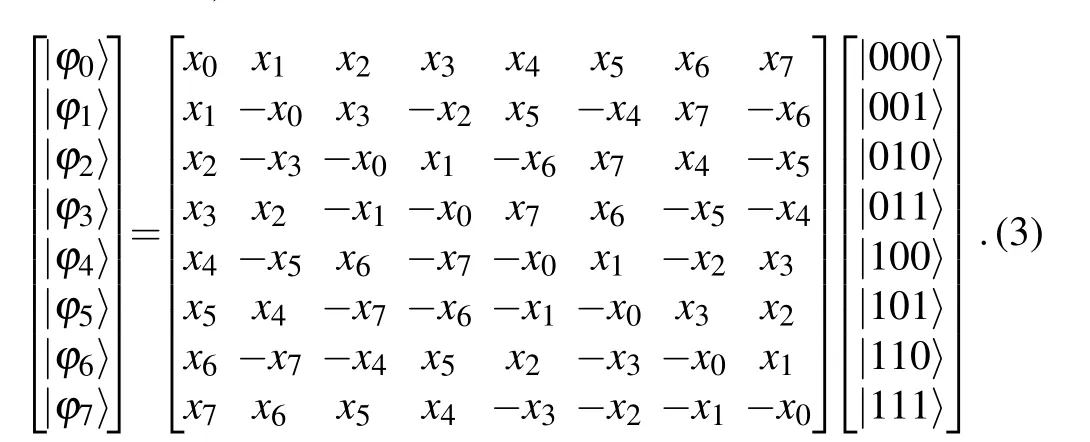
Next,according to her first measurement result,Alice chooses the projective measurement bases to measure her qubits,where a set of mutually orthogonal basis is given by

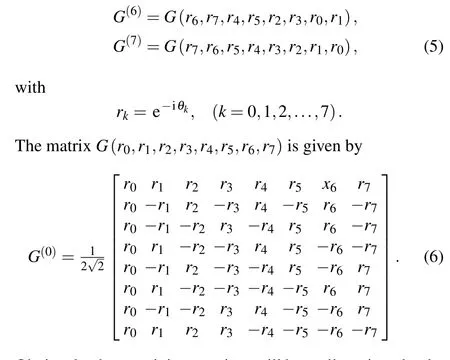


In this case, it is easy to see that Bob can always reestablish the target state with the same probability, provided that Alice’s projective measurement result is anyone of the sixty-four results.Then,according to the result,he can recover the original state|χ〉b1b2b3by suitable unitary operations. For instance, without loss of generality, when Alice’s measurement outcomes are|φ1〉⊗|η(1)2〉, Bob needs to perform the unitary operationZb1Zb2Xb3to restore the target state shown in Eq.(1). The relationship between the measurement results(MR)obtained by Alice and the necessary unitary operations performed by Bob(Ub)is shown in Table 1.
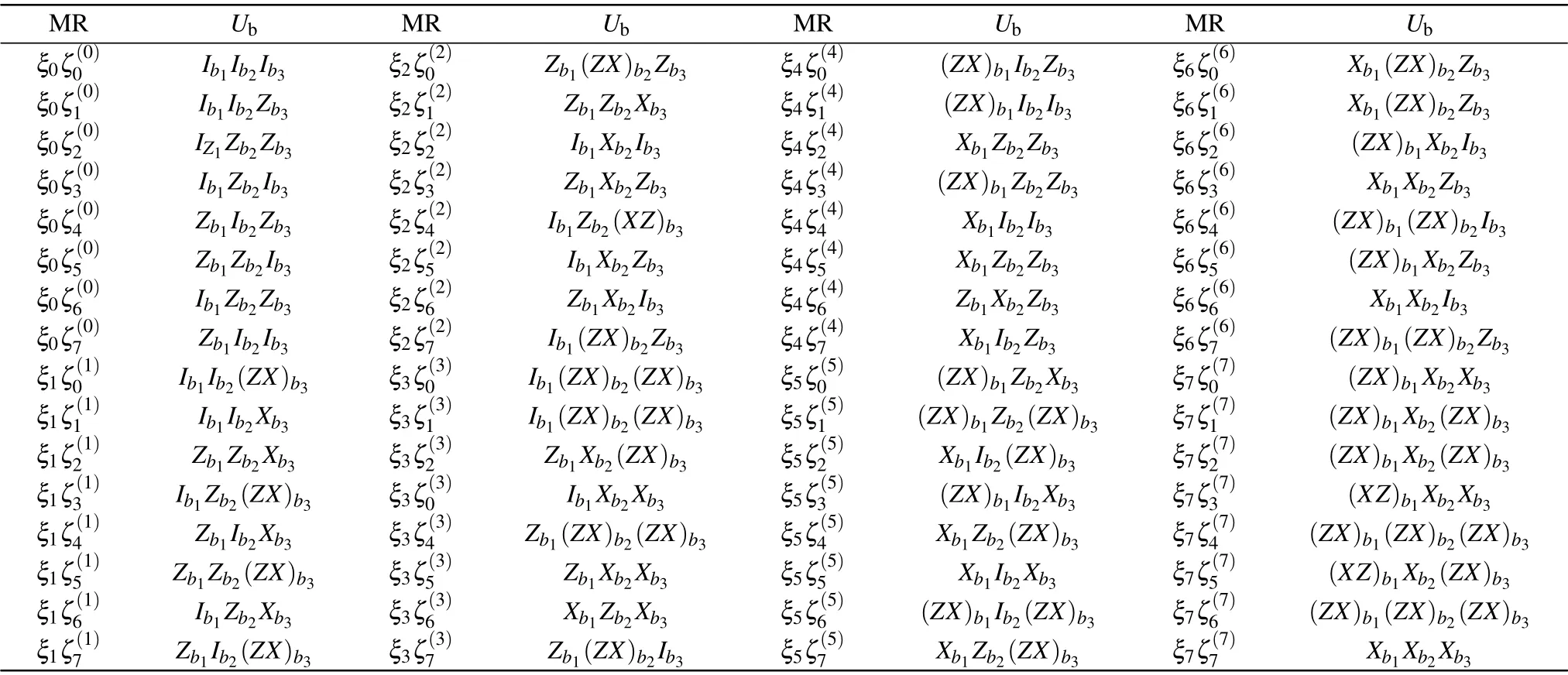
Table 1. Unitary operations (Ub) performed by Bob according to the measurement result (MR) of Alice. Here, ξi and ζ(i)j represent Alice’s measurement results|φi〉a1a3a5 and|η(i)j 〉a2a4a6,respectively.
3. RSP of an arbitrary three-qubit state in noisy environment
Quantum noise should be taken into account in actual communication. This section describes four types of quantum noises that are common in quantum channels: amplitudedamping,phase-damping,bit-flip and phase-flip noises.Quantum noise can be considered as a specific quantum operation that can be expressed in the form of operator summation. In order to determine the information loss,the fidelity in each situation is calculated. The DRSP of arbitrary three-qubit state is considered as follows.Alice is the source generator.She keeps qubits (a1,a2,a3,a4,a5,a6), and sends (b1,b2,b3) to Bob via the noisy channels. The noise on each channel is identical.Since the qubit pair(a1,a2,a3,a4,a5,a6)is not transmitted,it only takes into account the effect of the channel noise on the qubits(b1,b2,b3).
3.1. Density operators representation
We analyze the DRSP of an arbitrary three-qubit state in the form of density operators.[41]Alice distributes qubits to Bob through four kinds of noisy channels (bit-flip, phaseflip, amplitude-damping and phase-damping noisy channels,


3.2. The amplitude-damping noise
The amplitude damping noise describes the effect of energy dissipation due to energy loss in the quantum system.[45]The Kraus operators of the amplitude-damping noise are expressed as follows:

whereρdenotes the density matrix of the state described in Eq.(2),andEi,Ej,Ekdenote the noise operators acting on the transmitted qubits,and the superscripts represent the transmitted qubits. Following the similar steps(step 1 to 4 in this section),in the amplitude-damping noisy environment,the output state is

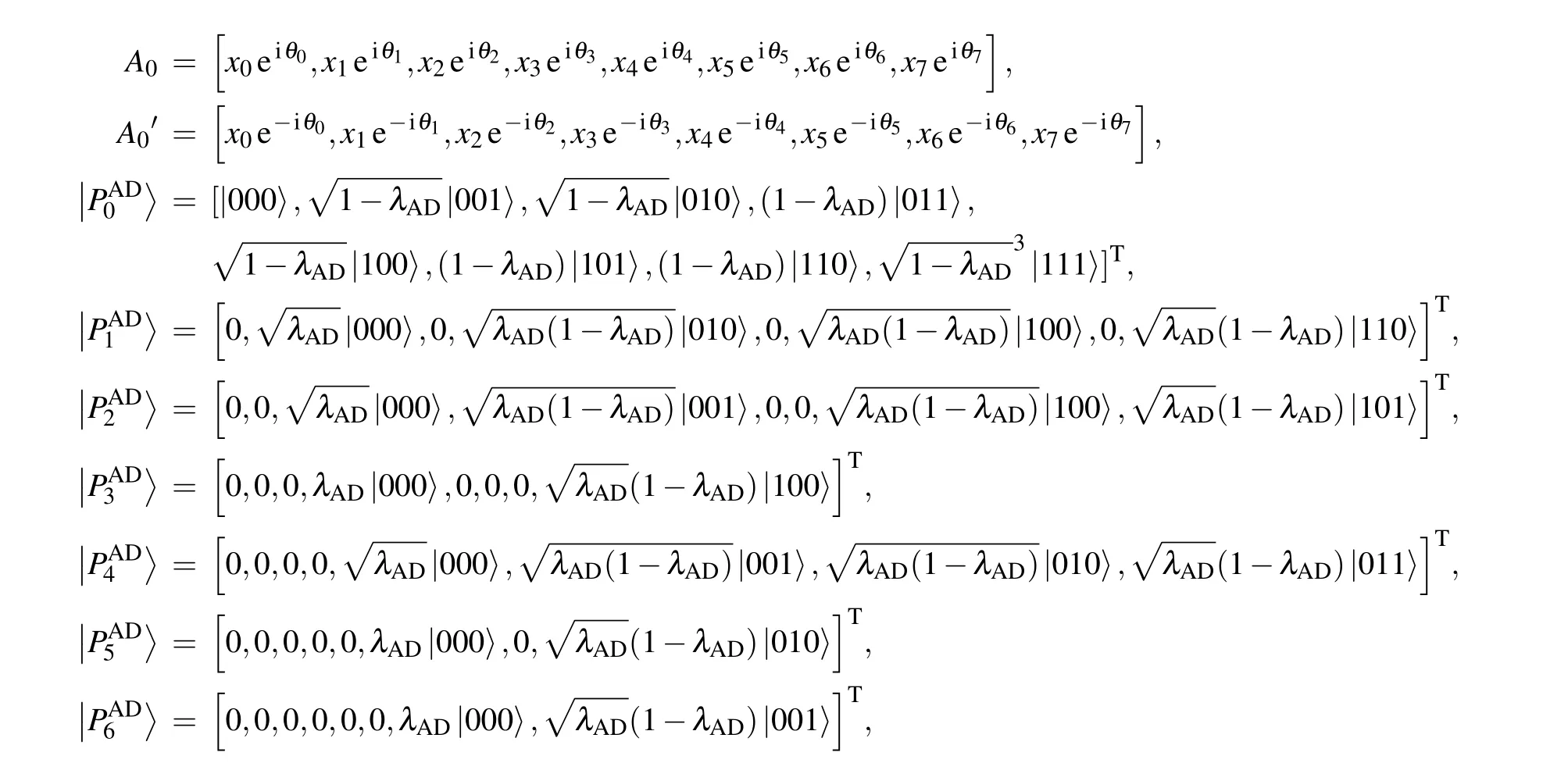
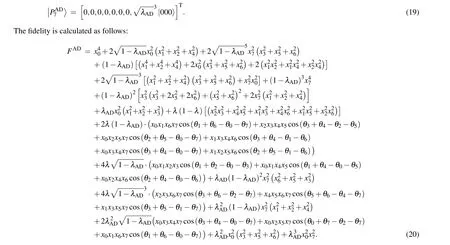
3.3. The phase-damping noise
In contrast to the amplitude-damping noise,the phase-damping noise simulates an interaction with the surroundings when energy loss is not involved.[44]The behavior of this noise is characterized by the following set of Kraus operators:

where




Following the similar steps, the fidelity is calculated as follows:
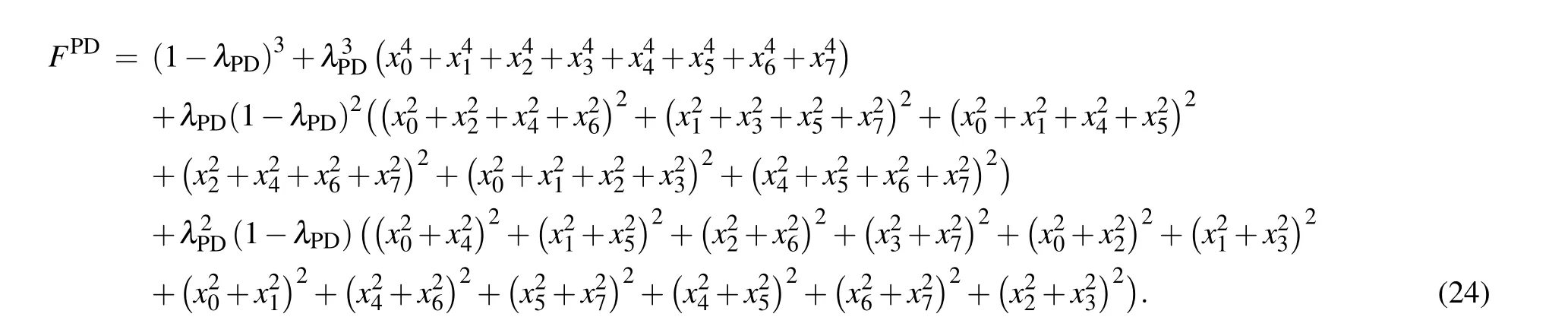
3.4. The bit-flip noise
The bit-flip noise changes a qubit from|0〉→|1〉or from|1〉→|0〉with the probabilityλBF,[45]and it can be described by the Kraus operators as

In the bit-flip noisy environment,the fidelity is too dedious to present here. We put it in Appendix A.
3.5. The phase-flip noise
The phase damping noise changes the qubit|1〉→-|1〉with the probabilityλPF, which describes the loss of quantum information that does not contain information loss caused by energy loss,[44]and its Kraus operators are
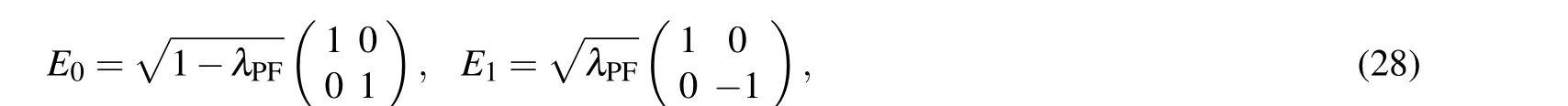

3.6. Analysis of noise impact


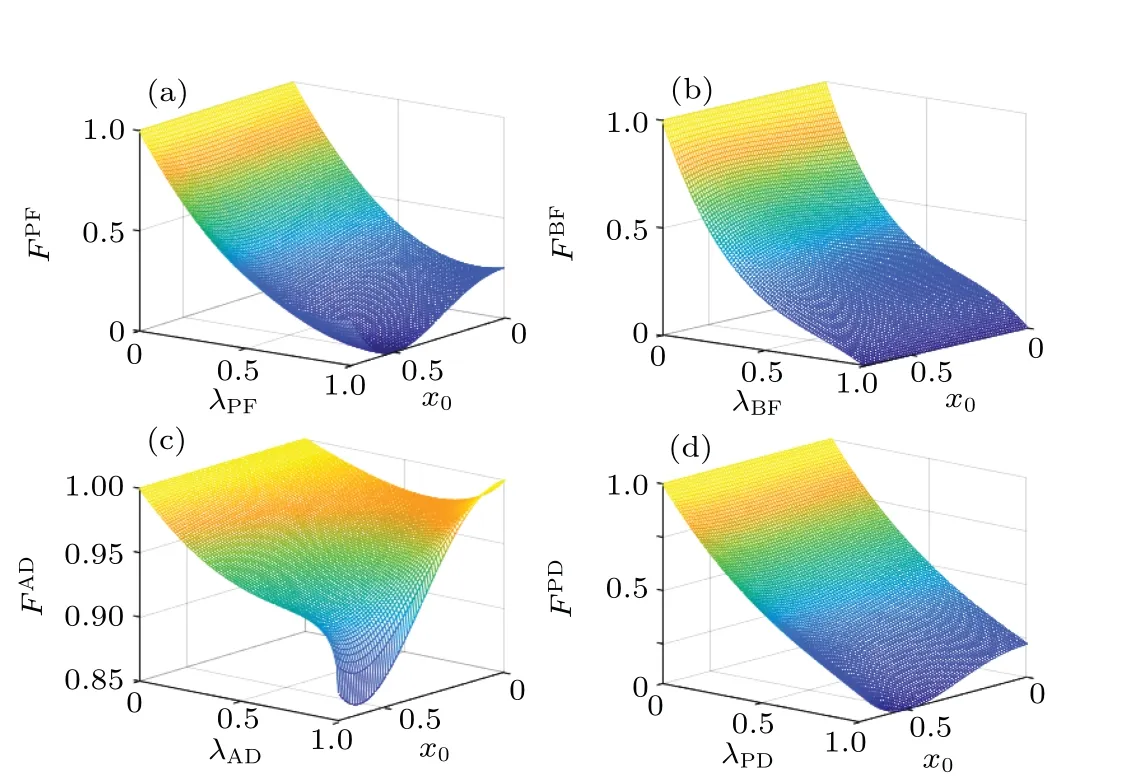
Fig.1. The fidelities of four-type noise channels with x0 and λ change for x0 ∈(0,],x1=,x3=x4= and x4=x5=x6=x7=0.

Fig. 2. Plots of the fidelities as a function of decoherence rate of amplitude-damping (yellow dotted line), phase-damping (greeen dotdash line), bit-flip (bule dashed line), and phase-flip (red solid line)noise channels with x0=x1=···=x7=
4. Conclusion
In summary, we have put forward a novel protocol for deterministic remote state preparation of arbitrary three-qubit state via one nine-qubit cluster-GHZ entangled state in ideal environment. We can realize the transmission of arbitrary three-qubit state which guarantees unit success probability in the meantime. In this study, two three-qubit projective measurements and appropriate unitary operations are required and only two classic bits are cost in classical communication. In addition, some attempts have been made to construct multi-particle channels, including cluster states and GHZ states,[31,33]which have made significant progress in both theoretical and experimental terms.In one sense,it shows the feasibility in the experiment in future.

Acknowledgements
This work was supported by the Tang Scholar Project of Soochow University, the National Natural Science Foundation of China (Grant No. 61873162), the Open Research Project of the State Key Laboratory of Industrial Control Technology, Zhejiang University (Grant No. ICT2021B24), and China Jiangsu Engineering Research Center of Novel Optical Fiber Technology and Communication Network and Suzhou Key Laboratory of Advanced Optical Communication Network Technology.
Appendix A
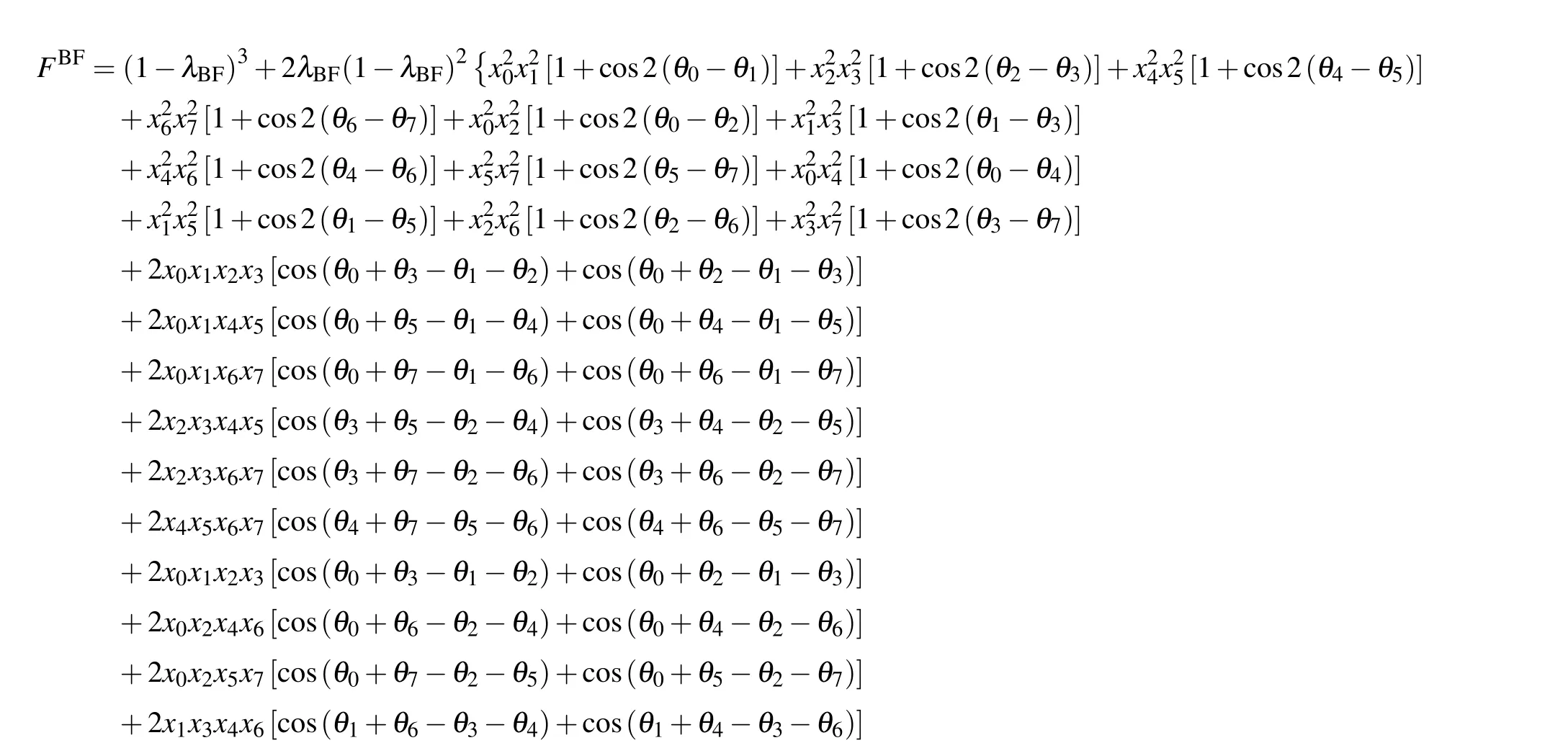

杂志排行
Chinese Physics B的其它文章
- Quantum walk search algorithm for multi-objective searching with iteration auto-controlling on hypercube
- Protecting geometric quantum discord via partially collapsing measurements of two qubits in multiple bosonic reservoirs
- Manipulating vortices in F =2 Bose-Einstein condensates through magnetic field and spin-orbit coupling
- Beating standard quantum limit via two-axis magnetic susceptibility measurement
- Neural-mechanism-driven image block encryption algorithm incorporating a hyperchaotic system and cloud model
- Anti-function solution of uniaxial anisotropic Stoner-Wohlfarth model
